Energy efficiency optimization of relay-assisted D2D two-way communications with SWIPT①
HE Jiai(何继爱), CHEN Yanjiao, WANG Tong
(School of Computer and Communication, Lanzhou University of Technology, Lanzhou 730050, P.R.China)
Abstract Aiming at the energy consumption of long-distance device-to-device (D2D) devices for two-way communications in a cellular network, this paper proposes a strategy that combines two-way relay technology (TWRT) and simultaneous wireless information and power transfer (SWIPT) technology to achieve high energy efficiency (EE) communication. The scheme first establishes a fractional programming problem to maximize EE of D2D, and transforms it into a non-fractional optimization problem that can be solved easily. Then the problem is divided into three sub-problems: power control, power splitting ratios optimization, and relay selection. In order to maximize EE of the D2D pair, the Dinkelbach iterative algorithm is used to optimize the transmitted power of two D2D devices simultaneously; the one-dimensional search algorithm is proposed to optimize power splitting ratios;an improved optimal relay selection scheme based on EE is proposed to select relay. Finally,experiments are carried out on the Matlab simulation platform. The simulation results show that the proposed algorithm has faster convergence. Compared with the one-way relay transmission and fixed relay algorithms, the proposed scheme has higher EE.
Key words: device-to-device(D2D), energy efficiency (EE), simultaneous wireless information and power transfer (SWIPT), two-way communications, power control, relay selection
0 Introduction
With the significant growth of wireless cellular equipment and its traffic demand, resource consumption and environmental pollution have also increased,cellular network is facing the challenge of spectrum resource shortage and high energy consumption[1].Therefore, it is of great significance to study green communication with high energy efficiency (EE). Device-to-device (D2D) communication technology that uses the cellular spectrum can effectively alleviates the problems existing in cellular networks, such as insufficient capacity, shortage of spectrum resources, poor communication quality of marginal users,and excessive energy consumption[2-4], but it brings various interference to cellular network. Simultaneous wireless information and power transfer (SWIPT) technology[5]can convert the harmful interference in the cellular network into beneficial energy source, thereby reducing system energy consumption and realizing green communication.
Relay technology,including one-way relay technology (OWRT) and two-way relay technology (TWRT)[6],effectively solves the communication problem when the distance between users is long or the link quality is poor. Research shows that, compared with one-way relay communication, two-way relay-assisted D2D communication can significantly improve the system performance (for example, spectrum efficiency (SE) and outage probability)[7]. However, due to the selfishness of the relay, it is unwilling to consume its energy to help other users. Thus, this paper combines the advantages of SWIPT and TWRT, and designs an optimization scheme that balances information and energy at the same time for energy-constrained relay nodes.
In recent years, scholars at home and abroad have conducted extensive researches on D2D relay-assisted communication based on SWIPT. Ref.[8] proposed a resource allocation and power control scheme for underlying D2D networks with SWIPT. Ref.[9] studied the SWIPT mode selection for energy-saving in D2D communication. Ref.[10] investigated the power allocation problem of D2D communication in cellular networks with SWIPT, and established a new game theory model to maximize utility. Ref. [11] optimized EE of D2D relay-assisted communication with power control,relay selection, and channel allocation algorithm.Ref.[12] studied on EE,SE of one-way and two-way D2D communication in a cellular network. It is a pity that the relay does not have an energy harvesting function. The above literatures used SWIPT or TWRT independently, not simultaneously. Ref.[13] deduced the outage probability of two-way D2D communication by using the spectrum sharing model of cooperative cognitive radio network, but the research on EE was not sufficient. In summary, although scholars have begun to study D2D communication based on SWIPT or TWRT,they have not done enough work on EE of D2D using SWIPT-TWRT at the same time. Moreover, the literatures lack research on joint consideration of power control, power splitting (PS) ratios, and relay selection.
To solve the above problems, this article aims at green communication, SWIPT-TWRT protocol for two D2D users exchanging information is proposed firstly,
where the idle D2D devices act as relays to scavenge energy from the radio frequency signals transmitted by both the users. According to the proposed strategy, an optimization problem is formulated to maximize the system EE by optimizing transmitted power and PS ratios.However, due to the coupling of transmitted power and PS ratios, it is hard to be solved. Therefore, the problem is decomposed into two subproblems: power control and PS ratios optimization. To reduce the complexity of relay selection, an improved optimal relay selection scheme based on EE is proposed, which considers not only EE of the system but also the distance. Experimental results show that this scheme can effectively improve EE of D2D links.
1 System model
Assume that there is a pair of D2D users (DU1and DU2) andnrelays for two-way communication in a cellular network, for example, the terminal uploads pictures while waiting to download the video,where the set of relays is denoted as {r1,r2, …,rn}.Because the distance is too long or the shadow fading is severe,there is no direct transmission link between DU1and DU2, it is necessary to use an idle D2D device as a relay node, and use decode-and-forward (DF) for auxiliary transmission. The system model is shown in Fig.1, which considers that a pair of D2D users reuse the uplink spectrum resources with less interference from cellular users in underlay mode, and limit a pair of D2D users to share the spectrum resources of only one cellular user at most. Each node in the system is equipped with an antenna and works in half-duplex mode.All channels obey the Rayleigh distribution, and the channel is flat block fading. That is, the channel coefficient remains unchanged within the timeTof completing a two-way transmission, and the channel has reciprocity. All devices have no power supply but can use the PS protocol in SWIPT technology for energy harvesting. It is assumed that the data buffer and battery capacity of the relay are infinite, so the overflow of data and energy is not considered.
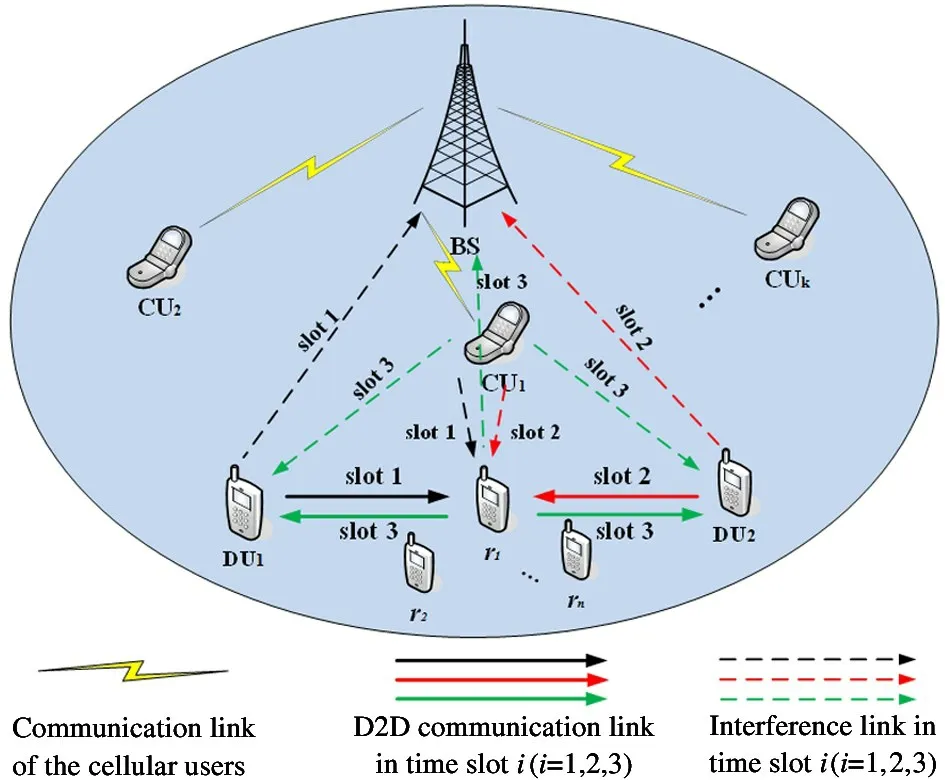
Fig.1 System model

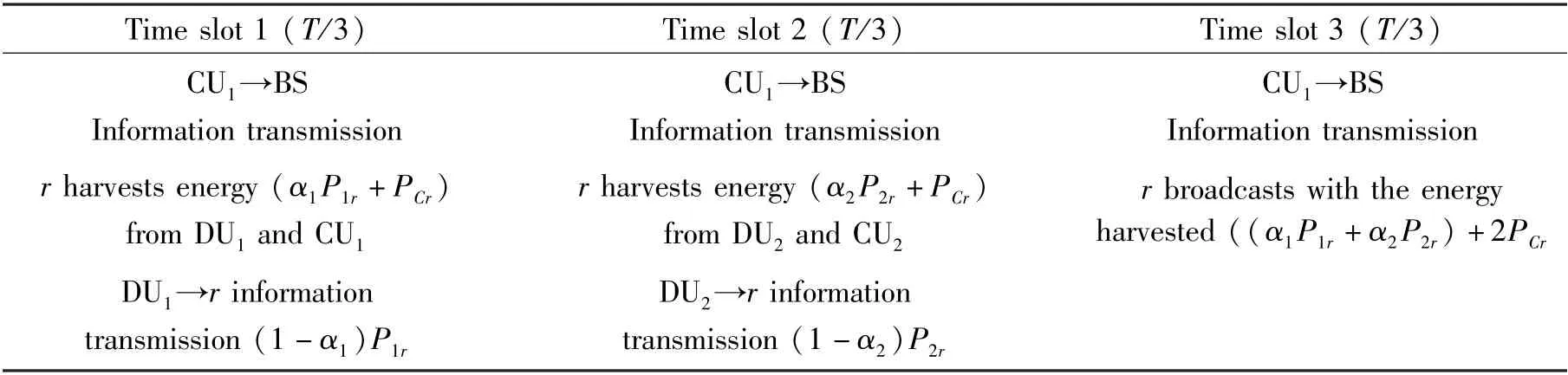
Table 1 PS time slot allocation table
2 Problem analysis
2.1 Signal model
According to the time slot allocation in Table 1, it can be analyzed that DUisends information torin time sloti(i=1,2).After processing by the receiver ofr,the signal received by the base station (BS) at the end of time slotiis written as


2.2 Energy efficiency model
Due to the fact that the transmission rate of the link depends on the transmission link with a low rate,at the end of the entire time slot, the transmission rate at DU1can be defined as

EE is defined as the ratio of transmission rate to power consumption, and its unit is bit/J. It means the number of bits that can be transmitted per unit of energy in a mobile communication system, which can be formulated as
In order to maximize the EE of the D2D pair and meet its transmission rate threshold, the power of each node needs to be solved when EE is maximum, the mathematical model is shown in the following formula.
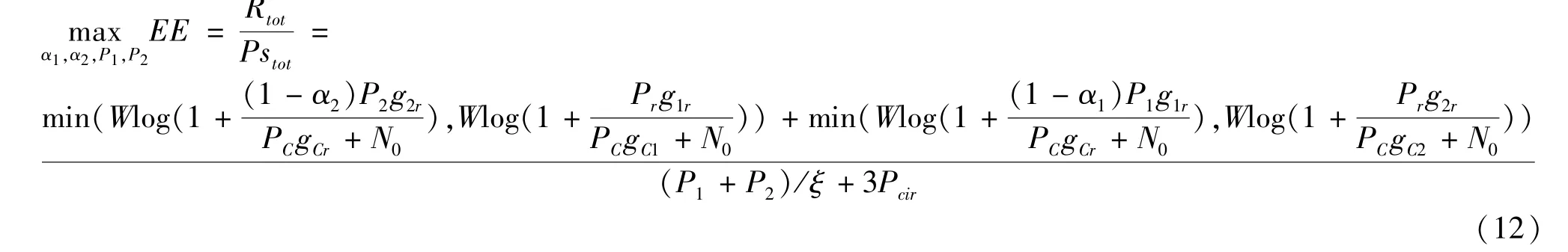
s.t.
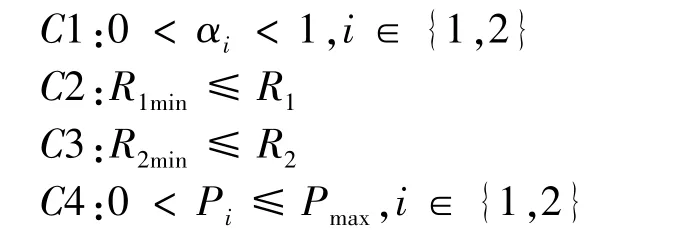
whereC1 presents the value range of the PS ratios,C2~C3 represent the minimum transmission rate threshold required by D2D users, and C4 represents the value range of transmitting power of D2D users.
3 Energy efficiency optimization
Since EE is a function of four variables ofP1,P2,α1,α2, it is difficult to solve Eq.(12). To simplify the solution of this problem, an iterative optimization algorithm can be used to obtain the maximum value of EE. The specific steps are as follows. In step 1,α1andα2are taken as fixed values.P1andP2are treated as optimization variables to optimize the objective function. In step 2,P1andP2obtained by optimization are regarded as fixed values.α1andα2are identified as optimization variables to optimize the objective function. In step 3, this iterative optimization is repeated,and optimization is completed until the final optimization result tends to convergence.
3.1 Transmitted power optimization
Whenα1andα2are fixed values, the optimization problem becomes
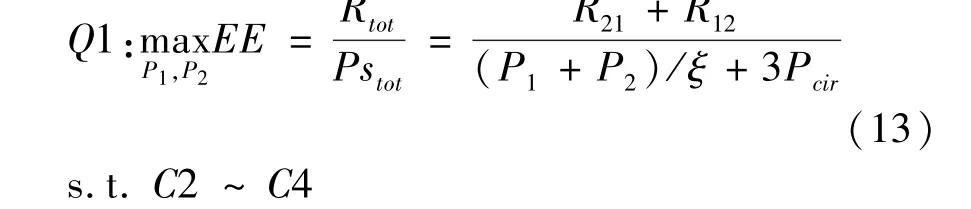
The objective function is a non-linear fractional function ofP1andP2.To facilitate the judgment of concavity or convexity, this formula is transformed into a non-fractional problem. Letq*denotes the maximum EE that can be achieved byQ1, and the function is defined as

It can be proved by Heisen matrix[15]thatQ2 is a convex optimization problem, and CVX toolbox[16]can be used in Matlab for optimization. Therefore, this paper uses an iterative algorithm based on Dinkelbach,and the specific process is shown in Algorithm 1.

Algorithm 1 The iterative algorithm based on Dinkelbach to maximize EE 1: Initialize the maximum iterations Lmax and the maximum error tolerance ε.2: Set the maximum EE q =0 and iteration index l =1.3: repeat 4: Solve Q2 with a given q by using CVX and obtain the optimal solution P′1 and P′2 5: if R′21 + R′12 - q × [(P′1 + P′2)/ξ +3Pcir] <ε, then 6: Set P*1 = P′1,P*2 = P′2,q* = R′21 + R′12(P′1 + P′2)/ξ +3Pcir,, l = l +1,Flag=0.Flag=1 and return 7: else 8: Set q = R′21 + R′12(P′1 + P′2)/ξ +3Pcir 9: end if 10: until Flag=1 or l =Lmax.
3.2 Power splitting ratios optimization
WhenP1andP2are fixed, EE is a concave function ofαi, the optimization problem can be rewritten as

The specific process is as follows. The transmitting powerP1andP2have corresponding PS ratiosα1andα2respectively. To solve the optimal EE,α1andα2are optimized one by one. First, the obtained optimal transmitting power of one D2D device and its PS are taken as fixed values, and optimize the value of EE under the PS of the other D2D device. Repeat the above steps, optimize the value of EE under the first PS ratios until its value is all traversed.
3.3 Relay selection
Due to the fact that the power and storage space of the device are limited,the design of the relay algorithm must be simple enough. Before selecting an appropriate relay for the D2D pair, to reduce the computational complexity, the candidate relay sets are divided for the D2D pair firstly. The optional relay deployment area division for DU1and DU2is shown in Fig.2. The area where the candidate relay is located is the overlapping area of two circles whose diameter is the distance between DU1and DU2and whose center is DU1and DU2.The relay nodes are randomly generated in this area on average, so the set of candidate relays for D2D users is expressed as
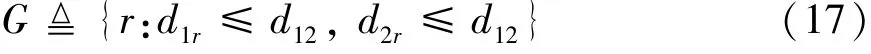
whered12is the distance between DU1to DU2,d1randd2rare the distance from DU1torand from DU2torrespectively.
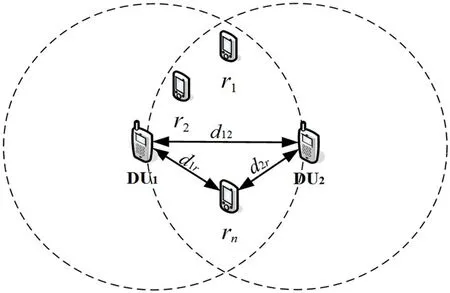
Fig.2 Alternative relay area
After dividing the candidate relay area for the D2D pair, |EEn| is used to represent EE of the D2D relay auxiliary link, and compare EE of each candidate relay to DU1and DU2. Under the condition of ensuring that the link reaches minimum transmission rate, this paper sorts in ascending order by the value of |EEn|and selects the relay node that can maximize EE of the D2D link. This relay node is the best one.
4 Complexity analysis

5 Simulation experiments and result analysis
The numerical results are shown to prove the superiority of EE with the proposed scheme. Matlab software is used to simulate the algorithm, the Monte Carlo experiment is repeated 1000 times, and then the results are averaged. To verify the advantages of the proposed scheme, EE of two communication modes and two relay modes are simulated respectively, and the influence of transmitted power, distance, and PS ratios on the performance of the algorithm is analyzed. To simplify the simulation, the relay node position is selected at the midpoint of the D2D pair in the fixed relay scheme. The main simulation parameters are shown in Table 2.relay selection schemes are adopted. The following conclusions can be drawn from Fig.3: (1) After 3 iterations, the algorithm has basically converged, so the proposed algorithm has faster convergence. (2) Comparing EE of one-way and two-way communication(same line) under the fixed relay and relay selection schemes, the results show that the two-way relay communication has higher EE than that of the one-way relay. (3) Comparing EE of fixed relay and relay selection (same symbol) in two-way communication and one-way communication, it can be concluded that EE has been further improved after adopting the scheme.
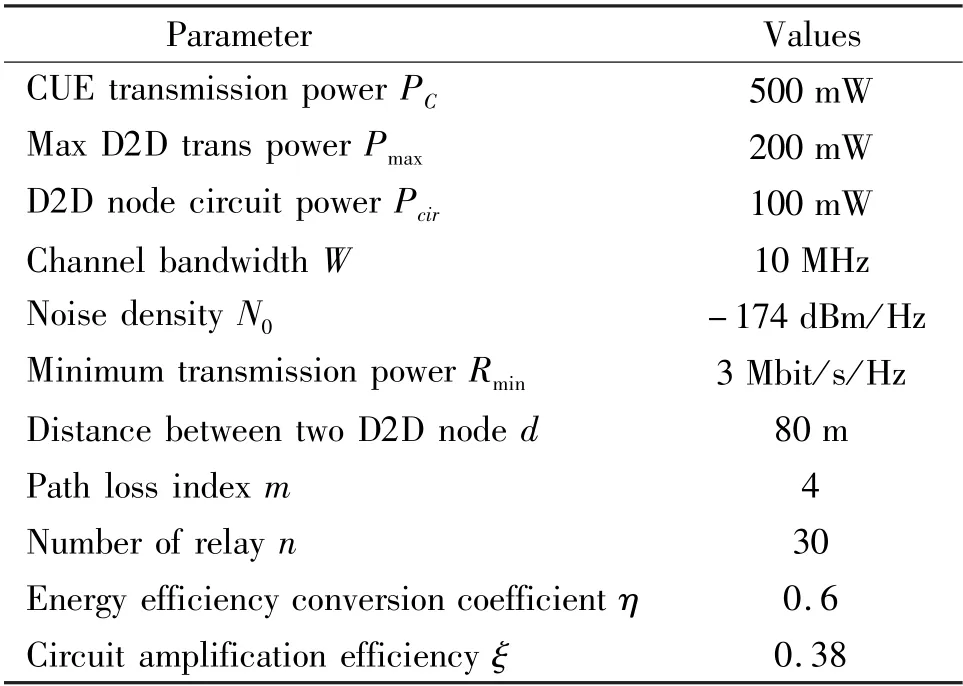
Table 2 Experimental simulation parameters
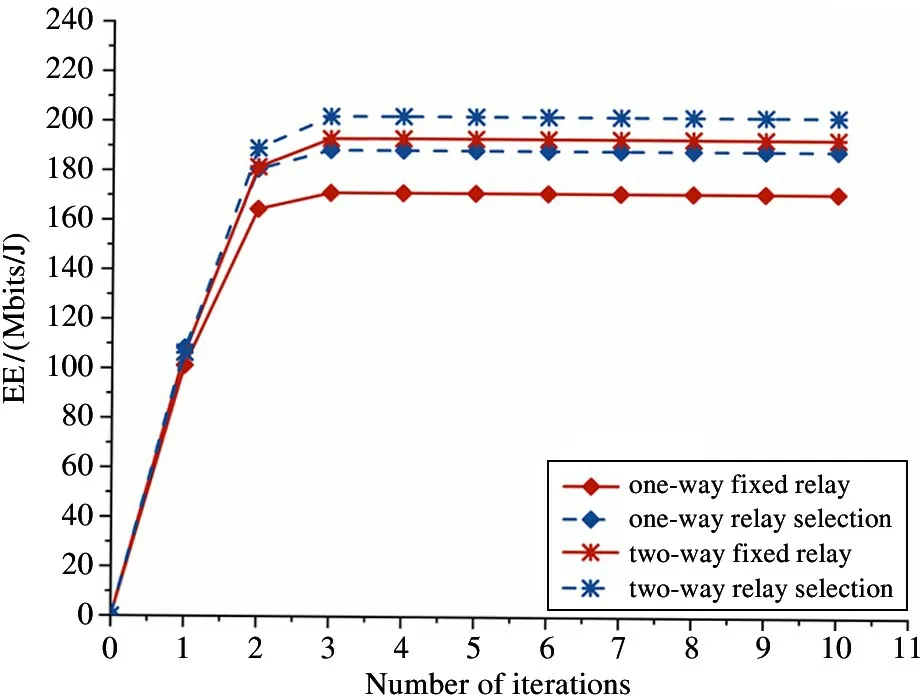
Fig.3 The relationship between the number of iterations and EE
In order to maximize EE of D2D communication,the optimal transmitted powerP1andP2of DU1and DU2are optimized simultaneously. Therefore, the optimal transmitted power of DU1and DU2in two-way communication and the transmitted power in one-way communication are simulated respectively when the relay is selected by the proposed scheme, as shown in Fig.4.In two-way communication, the relationship betweenP2and EE is plotted when the optimal value ofP1is fixed, and the relationship betweenP1and EE is also drawn when the optimal value ofP2is fixed. The following conclusions can be drawn from Fig. 4: (1)When the D2D transmitted power increases, after EE reaches the peak value for the first time, it decreases as the D2D transmitted power further increases. Thus,there is an optimal D2D transmitted power to maximize EE. (2) Compared with one-way communication,twoway communication can achieve greater EE with less transmitted power.
The distance of the D2D pair is set to 70 m,80 m,and 90 m respectively. Fig.5 shows the relationship between the distance and EE of the two-way relay selection scheme. It can be concluded from the figure that the closer the transmission distance between D2D users is, the greater EE will be. The main reason is that the longer the communication distance,the smaller the channel gain and the lower EE.
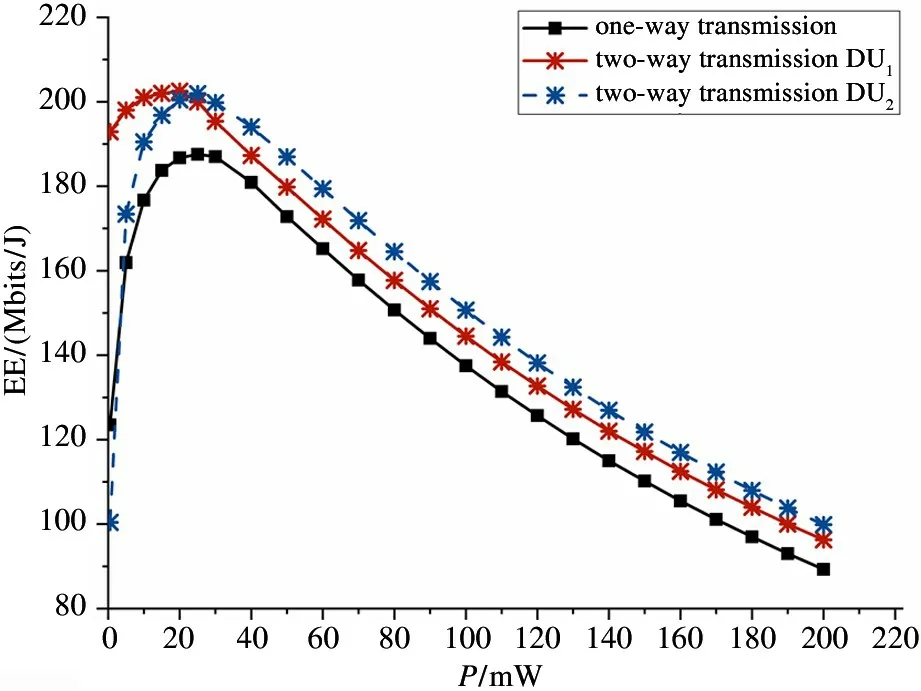
Fig.4 The relationship between transmitted power and EE

Fig.5 The relationship between distance and EE
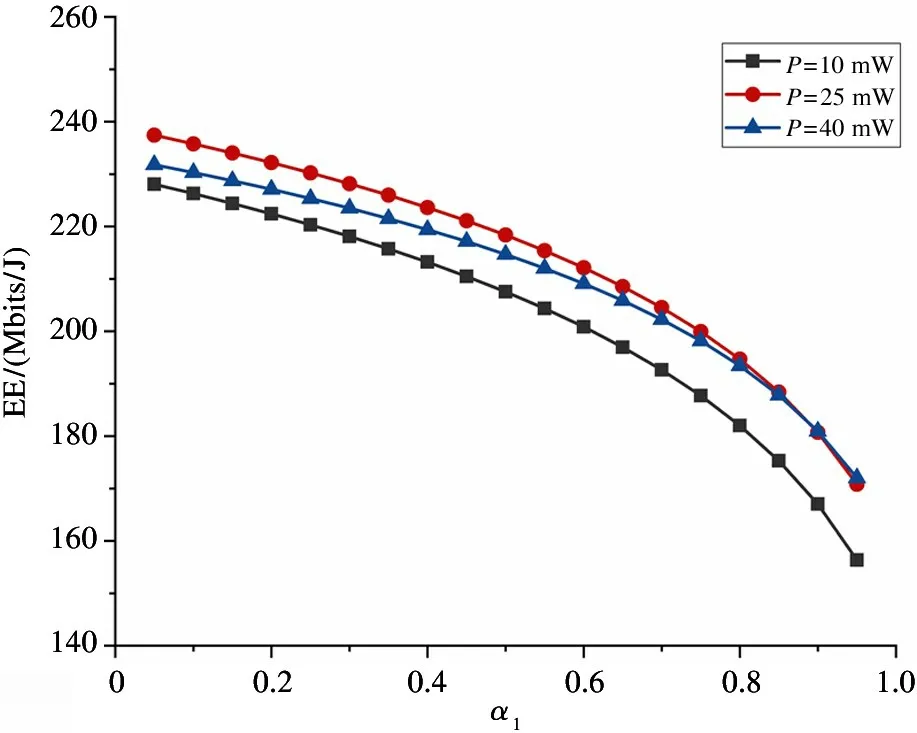
Fig.6 The relationship between PS ratios α1 and EE
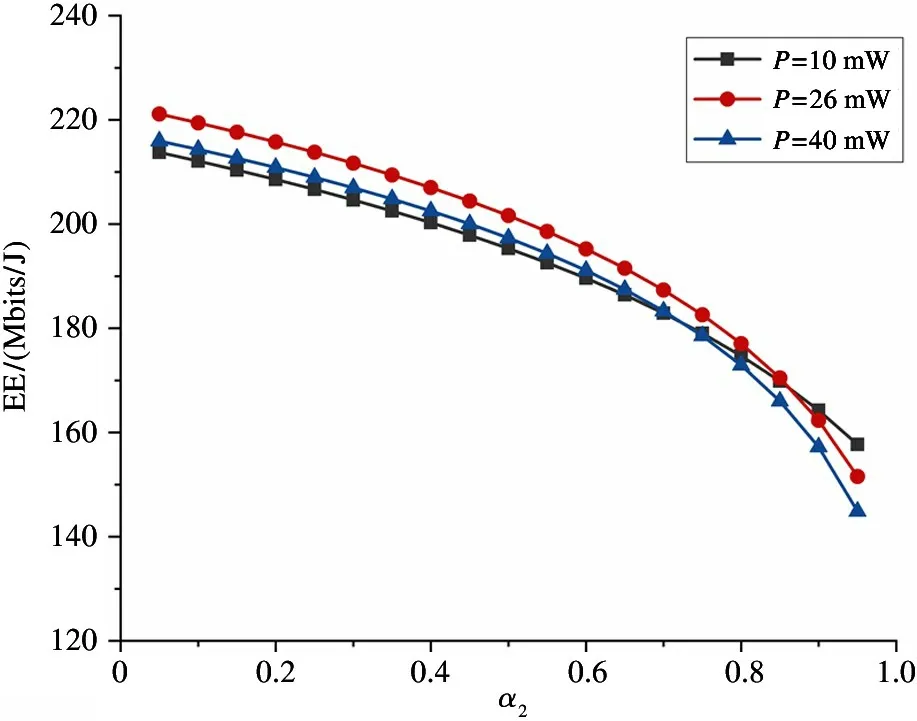
Fig.7 The relationship between PS ratios α2 and EE
Fig.6 and Fig.7 respectively represent the relationship between the PS ratios (α1andα2) and EE using two-way relay selection scheme. The optimal transmitted power of DU1and DU2isP1=25 mW andP2=26 mW respectively. Comparing EE under conditions of two different transmitted power values, which the one is larger than the optimal transmitted power and the other is smaller than the optimal transmitted power. The following conclusions can be drawn: (1) the largerαis,the lower EE is. That is, the greater the proportion of information decoding, the greater EE of D2D. (2)With the change of PS ratios, the value of EE is affected, which does not always maintain the optimal under the optimal transmitted power.
6 Conclusion
This paper investigates EE of two-way transmission of D2D user pair in a cellular network, and proposes TWRT-SWIPT protocols to reduce devices energy consumption. Simulation experiments verify the effectiveness of the two-way relay selection mode compared with other three modes: one-way fixed relay, one-way relay selection and two-way fixed relay. Thus, using TWRT-SWIPT protocols to the D2D communication can improve EE of the system. At the same time, this paper also analyzes the influence of transmitted power,distance, and PS ratios on the performance of the algorithm. In the next step, multiple D2D pairs of EE under the nonlinear energy harvesting model will be investigated to make the system model more valuable.
 High Technology Letters2022年3期
High Technology Letters2022年3期
- High Technology Letters的其它文章
- Multi-layer dynamic and asymmetric convolutions①
- Feature mapping space and sample determination for person re-identification①
- Completed attention convolutional neural network for MRI image segmentation①
- Efficient and fair coin mixing for Bitcoin①
- Deep learning based curb detection with Lidar①
- Research on will-dimension SIFT algorithms for multi-attitude face recognition①
