蝴蝶型钢拱桥主副拱肋交汇区域局部应力分析

陆 辉，覃枭雄

(广西南天高速公路有限公司，广西 南宁 530022)

0 引言

蝴蝶型拱桥是将竖直拱肋往桥外外倾而形成的一种新型异型拱桥，近年来，由于其造型美观，在实际桥梁工程中得到了大量应用[1-3]。通常，蝴蝶型拱桥采用中下承式无推力拱结构体系，拱肋主要采用钢箱截面形式。当跨径较大时，为保证结构的横向稳定，一般增设副拱，通过连杆与主拱相连。但由于增设副拱，使得主、副拱肋交汇，其交界处的应力分布十分复杂，无法通过杆系结构模型得到其实际应力分布状况，需借助实体或板壳模型有限元分析得到。另外，研究还表明，钢箱内的加劲肋构造会产生剪力滞效应，也会对应力分布产生影响[4-6]。本文以某中承式蝴蝶型拱桥为工程背景，建立主、副拱交界处的板壳有限元模型，对其在施工过程中的局部应力分布规律进行分析，并考察加劲肋构造的影响，以期为类似结构的设计分析提供借鉴参考。

1 工程概况

某大桥主桥为中承式钢箱拱肋混合梁系杆拱桥，主拱肋外倾斜12°成蝴蝶状，跨径为168 m，矢高为48 m，矢跨比为1/3.5；副拱肋轴线为空间曲线，跨径为130 m，矢高为20.742 m，矢跨比为1/6.268。主副拱肋之间的横向连杆采用圆钢管，桥型总体布置如图1所示。其主、副拱均采用钢箱截面，主拱肋截面尺寸为2.2 m×3.4 m，钢板壁厚为20～40 mm；副拱肋截面尺寸为1.5 m×1.5 m，钢板壁厚为16～20 mm，如图2所示。副拱肋截面自跨中向拱脚逐渐缩减，直至与主拱完全交汇。

2 有限元模型

利用ABAQUS程序建立有限元模型，钢板采用一阶4节点减缩单元S4R，不考虑焊缝的影响，如图3所示。有限元模型远离相贯线处的部分，采用几何结构化网格划分，靠近相贯线处部分，采用自由网格划分。有限元的模型边界条件为底部固结，上部主拱、副拱端施加由整体杆系结构计算得到的荷载，如表1所示。

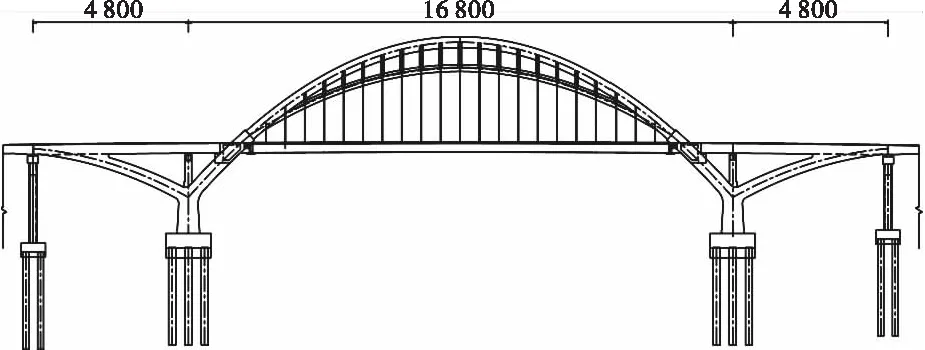
图1 桥型总体布置图(cm)

(a)主拱肋 (b)副拱肋图2 拱肋截面图(mm)

表1 主副拱肋施加荷载计算结果表

图3 有限元模型云图

3 计算结果及分析

3.1 主拱截面横向宽度方向应力

为分析主拱纵向加劲肋的剪力滞效应影响，选取如图4所示A-A～D-D四个截面沿横向宽度方向的应力分布图。由图4可以看出，虽然在加劲肋与顶板连接处出现折线状突变，但量值非常小，表明由纵向加劲肋产生的剪力滞效应影响很小；主拱肋外侧应力要明显大于内侧应力，表明主要还是受面内弯矩的影响。

图4 主拱肋截面应力分布曲线图

3.2 主副拱肋交汇区域的局部应力

为分析主副拱肋交汇区域在整个施工过程中的应力分布情况，选取拱肋悬拼、拱肋合龙、中跨系杆初张拉、安装吊杆及桥面纵横梁，通长系杆初张拉、中跨系杆二次张拉、铺桥面板、通长系杆二次张拉、桥面铺装、通长系杆三次张拉、成桥3 650 d等11个工况进行计算，并截取如图5所示A-A～D-D四个截面的应力变化计算结果。

图5 拱肋交界处截面应力计算结果云图

如表2所示为上述11个工况的计算结果。由此可以看出，从拱肋悬拼至中跨系杆初张拉，由于未安装吊杆及桥面横纵梁，总体上荷载水平较小，最大应力为75 MPa；从安装吊杆及桥面纵横梁至成桥3 650 d，应力呈增长趋势，中跨系杆二次张拉后，主拱肋应力会出现减小趋势，无论是主副拱肋的上限值还是下限值，均小于容许应力值。

表2 拱肋交界处截面应力计算结果表

3.3 主副拱肋交界相贯线的局部应力

为探讨施工过程中相贯线的应力分布情况，同样选取上述11个工况进行计算分析，结果如后页图6所示。从应力分布曲线图中可以看出，在主拱肋内侧及副拱肋顶部交界线处，距离起始3 m及6 m处出现应力峰值，其中，距离主副拱肋交界线起始端3 m处为吊杆钢板与主拱肋的交界处，距离主副拱肋交界线起始端6 m处为副拱肋横隔板与主副拱肋交界处。由此可见，外部构造对于应力集中影响明显。

4 结语

本文通过建立某蝴蝶型钢拱桥主副拱交汇区域的有限元模型，对其在施工过程的应力分布特点进行了分析，结果如下:

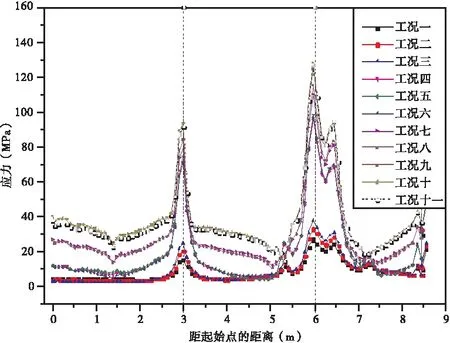
(a)主拱肋内侧交界线

(b)副拱肋顶部交界线图6 拱肋交界处应力分布曲线图

(1)通过对交界处主拱肋的应力分析，可以看出，主拱肋应力主要受弯矩影响，纵向加劲肋的剪力滞效应影响不大。

(2)从拱肋悬拼至中跨系杆初张拉，总体上荷载水平较小，从安装吊杆及桥面纵横梁至成桥3 650 d，应力呈增长趋势。中跨系杆二次张拉后，主拱肋应力出现减小趋势。

(3)主、副拱肋相贯线的应力分布表明，外部构造对应力集中的影响明显。工程实际中，应考虑吊点、主副拱交汇区域的设置，以减小其对应力集中的影响。