降水统计预报模型的模拟性能分析

陈以祺 吴香华 刘鹏 刘端阳

1 南京信息工程大学数学与统计学院，南京 210044

2 南京信息工程大学大气科学学院，南京 210044

3 南京交通气象研究所，南京 210008

1 引言

降水的科学有效预报，可以为工农业生产、水利开发和工程管理等有关部门减少不必要的损失。鉴于降水预报的重要性，学者们提出了各种各样的预报方法，其中最常用的就是数值预报和统计预报（Aparna et al., 2018）。数值预报牵涉大量的物理过程，计算量巨大，不确定性较高，传统统计预报计算过程较小，但其方法多以线性为主，难以处理降水这类非线性问题（白杨等, 2020）。随着计算机的飞速发展，人工智能迎来第三次发展浪潮，并在多个大数据分析领域中取得巨大成功，这也为该项技术与气象预报的结合提供了契机（孙健等,2021）。机器学习作为人工智能的重要分支，有效解决了降水预报的非线性和不确定性特征，在气象预报中的热度逐年上升（沈皓俊等, 2020）。基于机器学习的统计预报模型已被广泛应用于降水中，亟需从云降水物理学和统计学的角度，对降水的统计预报模型进行科学可靠的性能评估。

机器学习方法可以挖掘海量气象数据中的潜在规律，在降水发生预报领域的效果显著。神经网络以优良的自学习、自组织、容错性和非线性逼近能力广泛应用于降水的预报中，尤其是BP 神经网络（Back Propagation Network，BPNN），通过信号向前传播以及误差反向传播的不断迭代训练出整个预报模型（杨永生和何平, 2008; 李宁, 2011; 石晓燕等, 2013）。研究表明，无论是基于降水量历史数据还是气象资料，BPNN 均能够成功预报出未来的降雨量且预报准确率较高（张辉, 2013; 葛彩莲等,2010; 黎玥君和郭品文, 2017; 李嘉康等, 2017；刘莉和叶文，2010）。支持向量机（Support Vector Machine，SVM）通过采用线性算法构建超平面，高维甚至无限维空间，并基于核技巧将初始数据集投射到高维或无限维的希尔伯特空间，得到一个非线性输入数据空间的算法（李万庆等, 2007; 倪远臣, 2014; 胡凤良等, 2017），使得 SVM 非常适合具有复杂非线性特点的降水预报建模。相较几种基于常规神经网络计算的方法而言，SVM 在日降水量预报中具有优越性（杨淑群等, 2006; Ortiz-García et al., 2014;Hamidi et al., 2015; 许晓宁, 2018）。相比于神经网络和支持向量机收敛速度较慢的特点（史逸民等,2018），决策树（Decision Tree，DT）收敛速度快，计算复杂度低，对于降水预报效果较好（Kusiak et al., 2009; 何东坡, 2016; Choubin et al., 2018）。除此之外，随机森林（Ho et al., 2014; He et al., 2016）、极限学习机（孔德萌等, 2017）、朴素贝叶斯（周丽莉等, 2017; Voyant et al., 2017）等机器学习方法也逐渐被应用于降水预报中。

但是，就目前的降水预报工作而言，将机器学习和统计模拟方法相结合，对模型的预报性能进行分析和比较的研究较少。相关的研究主要有：基于交叉验证技术的KNN（K-Nearest Neighbor）方法在一定程度上可以减少降水预报的空报率，使预报效果显著提高（曾晓青等, 2008）；采用相关加权，多元线性回归以及支持向量机回归与“交叉验证”相结合的方法，开展有限区域模式的多模式短期超级集合预报研究（陈超辉等, 2010）；借助交叉验证手段评估夏季降水预报效果的稳健性（朱连华等, 2015）；采用10 折交叉验证方法计算决策树的预报准确度，进而评估不同降水预报决策树的性能（张佳华等, 2017）；采用LOO（Leave-One-Out ）交叉验证选择模型，并用选定的模型修正TRMM（Tropical Rainfall Measuring Mission satellite）数据，以获得最接近“真值”的降水估计值（范科科等, 2017）。但是，这些研究或针对模型参数的调优和最优参数的选取，或针对模型性能指标的计算和模型的选择，并没有涉及在模型性能最优的条件下，对模型的预报性能进行比较。

因此，在实际的降水预报工作中，建立可靠的预报模型，并对模型的预报性能做出客观评价，是一个不可忽略并亟待解决的问题。另一方面，黑龙江省位于亚洲东部，易受强盛的季风气候影响，冬季干冷，夏季降水充沛（韩玉梅, 2008）。同时，黑龙江省也是中国重要的粮食作物产区，夏季是粮食作物的生长关键期。因此，对黑龙江省夏季降水的准确预报对农作物产量提高具有深远的战略意义。鉴于以上情况，本文基于我国黑龙江省2015～2019 年夏季逐日降水站点数据，拟从统计学角度出发，采用统计模拟技术，分析基于BP 神经网络、支持向量机和决策树的3 种降水统计预报模型的性能，研究支持向量机逐日降水预报模型性能空间分布。为统计预报模型的性能评估，提供一种科学有效的实验估计方法。

2 资料和方法

2.1 资料

本文采用的资料来源于国家气象科学数据中心（http://data.cma.cn[2020-11-05]）提供的中国地面气候资料日值数据集，包括20:00（北京时间，下同）至次日20:00 降水量、平均气温、平均气压、平均相对湿度和平均风速5 个气象要素。选用黑龙江省（43°N～54°N，121°E～136°E）28 个地面基本气象观测站及自动站的逐日观测数据，资料选取时段为2015～2019 年夏季（6～8 月），图1 为黑龙江省气象站点分布。依据20:00 至次日20:00 降水量数值大小，将降水事件划分为发生（降水量＞0 mm/d）和不发生（降水量=0 mm/d）两类，以降水是否发生为研究对象，平均气温、平均气压、平均相对湿度和平均风速为预报因子，建立降水统计预报模型。为了消除量纲、单位不同以及数据缺测给预报结果带来的影响，对预报因子进行标准化预处理和质量控制。

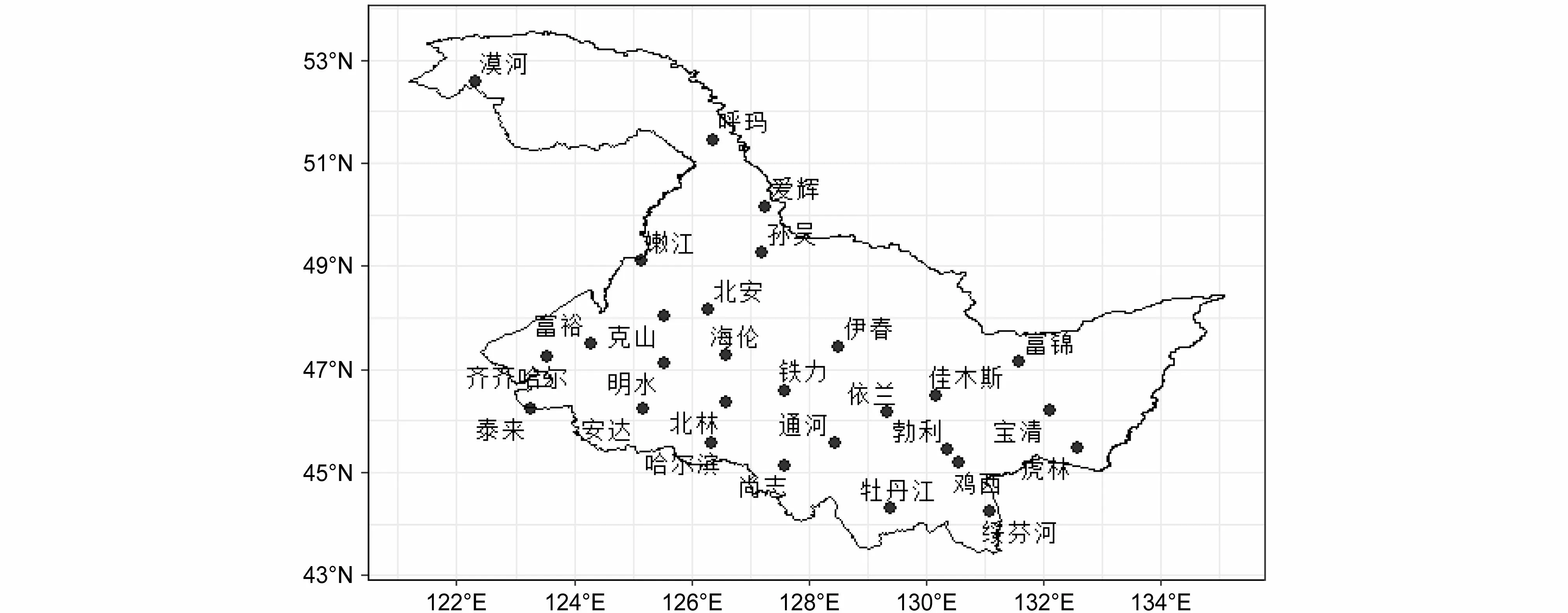
图1 黑龙江省气象站点分布Fig. 1 Distribution of meteorological stations in Heilongjiang Province

2.2 统计模拟方法

本文所用的性能评估方法主要有留出法（Holdout）、自助法（Bootstrap）和交叉验证法（Crossvalidation）（梁子超等, 2020）。其中留出法和自助法用于模型训练集（training set）和测试集（testing set）的划分，交叉验证法用于模型参数调节。

在同一数据集上对模型进行训练和性能评价，缺乏模型泛化能力的分析。因此，在另一个数据集上对模型进行统计模拟评价，可以有效避免训练样本和测试样本交叉而导致的过拟合。留出法、自助法和交叉验证法3 种Monte Carlo 模拟抽样的方法可以用于评估所有模型的预报性能。基本思想是把原始数据集划分为两个互斥的子集，其中一个子集作为训练集，另一个子集作为测试集。一般而言，基于自助法的预报模型的性能分析相较于留出法更加客观且有说服力。

留出法是一种随机的非重复抽样方法，是最早提出的统计模拟方法的基础，它仅取决于数据的一次分割结果，由于没有交叉处理，也被称为验证方法。留出法的具体做法为：首先将数据集随机划分为两组，分别作为模型训练集和测试集；然后用不同的统计学习方法在模型训练集上构建模型，得到不同的训练模型；最后用训练模型拟合测试集，计算出模型的预报误差，以此评估模型性能。一般而言，训练样本量越大，预报模型的性能越好；测试样本量越大，误差估计越准确。因此，测试误差大小与数据划分比例有很大关系，本文选用的划分比例为7:3。留出法在进行模型的建立和评估时，存在一些众所周知的局限性：第一，留出法将数据随机分为了数量不同的两组，数量较少的一组用于模型评估，数量较多的一组用于训练模型，由于训练模型的样本数据偏少，建立的模型比不上使用全部数据建立的模型好。第二，训练的数据越少，模型的方差就会越大，反过来，训练的数据越多，模型的性能越不可靠。因此，训练集与测试集的划分很可能成为模型优劣的重要因素。为了弥补留出法抽样的局限，可以采用重抽样的方法。

自助法是一种有放回的重抽样，以自助采样法为基础。具体做法为：在样本数量为n的数据集中随机选取一个样本，放入模型训练集中，然后再将该样本放回到数据集中，参加下一次的抽样，抽样n次 后，将会形成一个容量为n的新数据集，将这个新数据集用作模型训练集。如此一来，某些样本在测试集中可能重复出现，也有可能从不出现。由于每个样本每次被抽中的概率n-1和不被抽中的概率1-n-1都是相等的，因此，n次抽样之后，样本不被抽中的概率为(1-n-1)n，当n→+∞ 时，样本未被抽中的概率为 e-1，约等于0.368，这样实际评价的模型与期望评价的模型都使用n个训练样本，而测试样本约为总样本的36.8%。

模型参数的不同设置，往往会导致性能的显著差别。因此，对模型性能进行评价时，需要先对模型的参数进行调节。交叉验证是目前应用最为广泛的模型参数调节方法。它是一种简单地重复抽样的方法，具体做法：首先决定一个折数S，并将训练数据切分为S个相互独立的均等子集；然后取其中一个子集作为测试集，剩余S-1 个子集的数据作为训练模型的训练集，不重复地取S次后，可以得到S个模型和它们的测试误差；最后选择S次评测中测试误差最小的模型参数。由于每一个样本数据既用于模型的建立又用于模型的参数选择，所以交叉验证能够有效地利用样本数据。

2.3 性能度量指标

为了评估统计模型的性能，需要相应的性能度量指标。对于二分类模型而言，混淆矩阵、精度、准确率、敏感度、特异度、F1 分数、ROC（Receiver Operating Characteristic）曲线及ROC曲线面积是最常用的性能度量指标。本文主要选取了其中的准确率（accuracy）、敏感度（sensitivity）、特异度（specificity）、ROC 曲线和ROC 曲线面积。其中，准确率表示降水统计预报模型准确识别出降水是否发生的比例，是对降水统计预报模型准确率的评估；敏感度表示实际发生降水并且被准确识别的比例，衡量的是模型对发生降水的判别能力；特异度表示实际不发生降水并且被准确识别的比例，衡量的是模型对不发生降水的判别能力。ROC 曲线是针对样本类别分布不平衡而提出的，它综合考虑了敏感度和特异度的特点，以敏感度为横坐标，1-特异度为纵坐标绘制而成，曲线越陡峭，越高耸，越接近直线y=1模型的性能越高。ROC 曲线面积是一个概率，是对ROC 曲线的量化。一般而言，ROC曲线面积的取值越大，模型的预报性能越好。基于上述原因，本文降水统计预报模型的性能评价综合指标为ROC 曲线面积。

为了对3 种降水统计预报模型性能进行比较，本文采用ROC 曲线面积显著性检验方法对模型的ROC 曲线面积进行比较检验。ROC 曲线面积显著性检验方法主要包括以下几个操作步骤：首先，计算出3 种降水统计预报模型的ROC 曲线面积和曲线面积方差，并将BPNN、SVM、DT 的ROC 曲线面积分别记为A1、A2、A3； ROC 曲线面积方差分别记为V1、V2、V3。其次，计算出任意两个模型的ROC 曲线面积差值θ和协方差。BPNN、SVM、DT 的θ分别记为 θ1、 θ2、 θ3；协方差分别记为C1、C2、C3。然后，计算出任意两个模型的Z值，BPNN、SVM、DT 的Z值分别记为Z1、Z2、Z3，其中，Z1的计算公式如下：

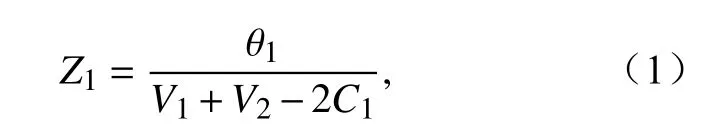
其余Z值的计算公式与之类似。最后，对Z值作显著性检验，得到P值，P表示两个降水统计预报模型的ROC 曲线面积存在差异的可能性，一般认为P＜0.05，两个降水统计预报模型的ROC 曲线面积差异有统计学意义；P＜0.01，两个降水统计预报模型的ROC 曲线面积差异显著；P＜0.001，两个降水统计预报模型的ROC 曲线面积差异非常显著，反之亦然。

3 降水统计预报模型的建立

利用留出法和自助法将黑龙江省夏季28 个站点的所有数据依次划分为训练集和测试集，在训练集上对模型进行参数调优，用测试集上的判别效果估计模型在实际使用过程中的泛化能力。综合考虑数据集样本容量较大、3 种统计学习方法容易过度拟合的特点，在模型的构建中采用了重抽样方法。重抽样方法在大样本中的差异性不明显，与其他几种重抽样方法相比，10 折交叉验证的方差适中，获取模型最优参数的计算速度较快，可以有效避免过拟合现象的发生。因此，降水统计预报模型的模型参数调节方法为10 折交叉验证。

3.1 BPNN 降水统计预报模型的构建

BPNN 无需提前给定映射关系方程，就能学习和存贮大量的映射（陈茜等, 2018），对于海量气象数据的处理效果较好。Hecht-Nielsen（1989）证明了一个输入层、一个隐含层和一个输出层的三层神经网络可以解决任意复杂的非线性问题，并且拥有很强的非线性映射和自适应学习能力（李宁,2011）。在3 层BPNN 降水统计预报模型的构建中，需要选取的模型参数有隐含层神经元节点数N以及权值衰减参数（Decay，D）。

BPNN 模型建立最为重要的就是N的确定，N较多，容易导致过度拟合和计算量过大的问题，N较少，模型性能又不容易达到预期的效果。目前对于N的选择没有特定的公式，基于降水预报的多种特征，综合考虑多种因素，本文给定N的范围为

其中，nI和nP分别为BPNN 输入层和输出层的神经元节点数。根据公式（2）可知，N的选取范围为[4，12]。权值衰减参数是为了避免BPNN 在训练过程中发生过拟合的情况而给误差函数添加的一个惩罚项。目前对于权值衰减参数的选取尚没有普适的公式，常用的权值衰减参数取值为0.5、0.1 和0.01。

采用试错法确定N和权值衰减参数的最优组合，建立参数最优的BPNN 降水统计预报模型。根据不同的参数组合训练不同的模型，然后选择准确率最高的参数组合。通过不断地对比和调试，可以得到N和权值衰减参数不同组合下拟合模型的统计量。特别地，Kappa 系数是对准确率的修正，是衡量模型一致性的指标，它消除了正确分类的随机性因素，数值越大，代表模型的预报效果越好。由图2a 和图2c 容易获悉：基于留出法的BPNN 模型隐含层节点数为12，权值衰减参数为0.5 时，模型的准确率和Kappa 系数最大，最优参数组合为N=12，D=0.5；由图2b 和图2d 容易获悉：基于自助法的BPNN 模型隐含层节点数为11，权值衰减参数为0.1 时，模型的准确率和Kappa 系数最大，最优参数组合为N=12，D=0.01。

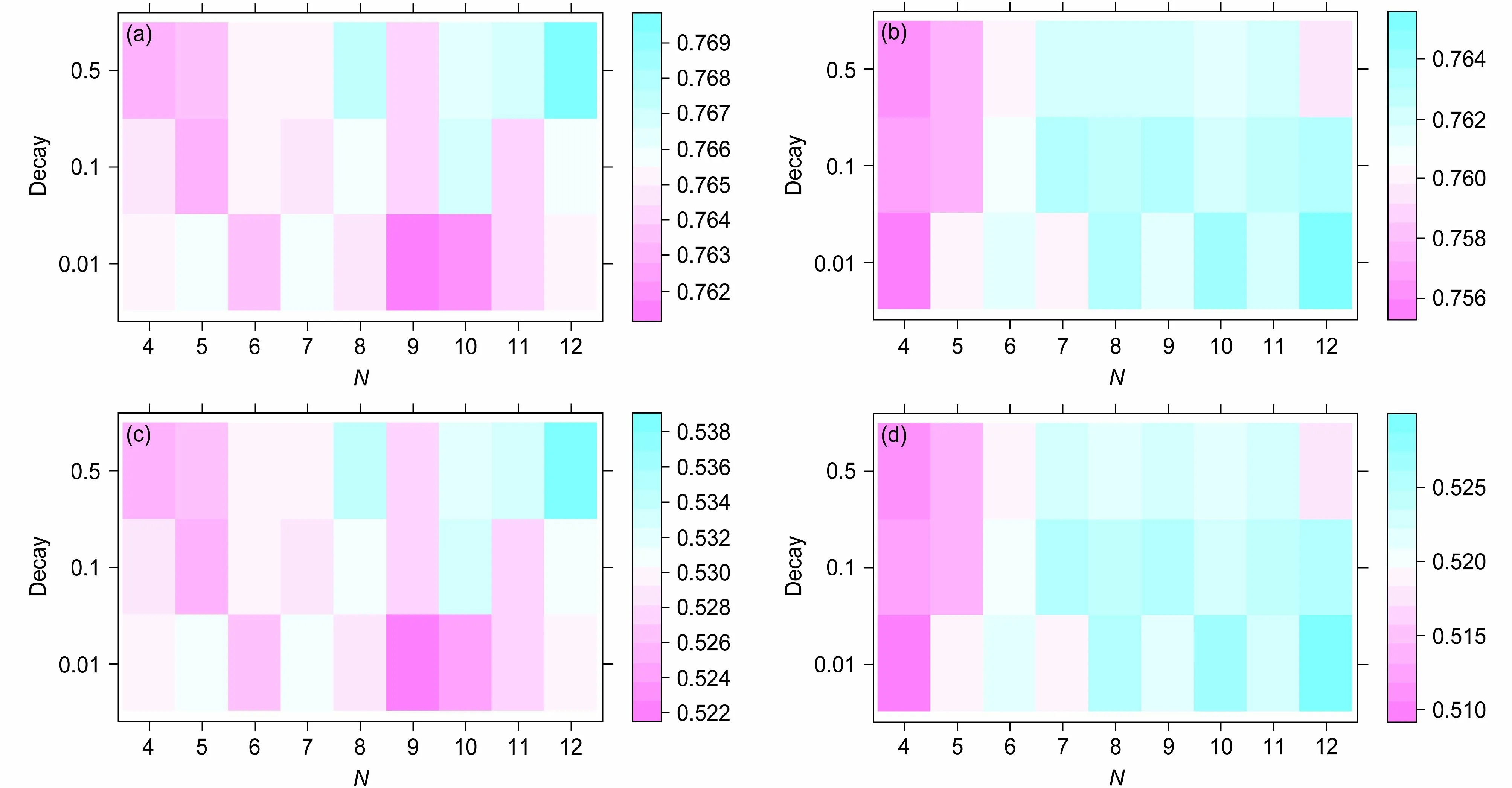
图2 2015～2018 年黑龙江省夏季逐日降水量基于留出法（左列）和自助法（右列）的BPNN 统计预报模型的参数调优：（a、b）准确率热力图；（c、d）Kappa 系数热力图Fig. 2 Parameter tuning of the BPNN statistical prediction model of daily summer precipitation in Heilongjiang Province from 2015 to 2018 based on Hold-out (left column) and Bootstrap (right column) methods: (a, b) Thermal maps of accuracy; (c, d) thermal maps of Kappa

3.2 SVM 降水统计预报模型的构建

SVM 良好的鲁棒性和泛化性能使其在近年来的降水预报等相关领域得到了广泛的应用。SVM的特点在于采用了工程问题上的核函数。使用核函数可以将数据映射到高维空间，使非线性的数据在高维空间线性可分，并能够有效提高模型的预报精度。除此之外，SVM 惩罚因子的选择可以降低模型的分类误差以及可以更好地控制分离边界。

常用的核函数有：线性核、多项式核、径向基核和神经网络核。由于径向基核函数可以用来解决目标变量和预报变量间的非线性关系，是一种非线性的映射，适用于不同规模的样本量和不同维度的样本空间。无特殊要求，一般选择径向基核函数。除了核函数的选择以外，惩罚因子和Sigma 参数的选择也可能成为SVM 模型预报性能的影响因素。惩罚因子是用来惩罚错误分类的训练样本的。一般而言，如果惩罚因子的数值较大，那么分类的间隔相应的就会较小，错分样本的比例就会增大；相反，当惩罚因子的数值减小时，分类的间隔就会变大，错分样本的比例也会相应的减少。因此，惩罚因子的大小直接影响模型分类的误差和分类间隔的大小。Sigma 参数决定着分类界限的形状和平滑程度，Sigma 越大，平滑程度越好。一般地，Sigma 参数设置的依据是Schuldt et al.（2004）提出的Sigma参数合理估计解析公式。

为了调优SVM，主要设定了10 个惩罚因子取值。通过不断地对比和调试，可以得到不同惩罚因子参数值下拟合模型的统计量。由表1 容易获悉：基于留出法的SVM 模型惩罚因子取值为2，设置Sigma参数为0.3332 时，模型的准确率和Kappa 系数最大，取值为76.94%和0.5381；基于自助法的SVM模型惩罚因子取值为64，设置Sigma参数为0.3158时，模型的准确率和Kappa 系数最大，取值为77.47%和0.5481。

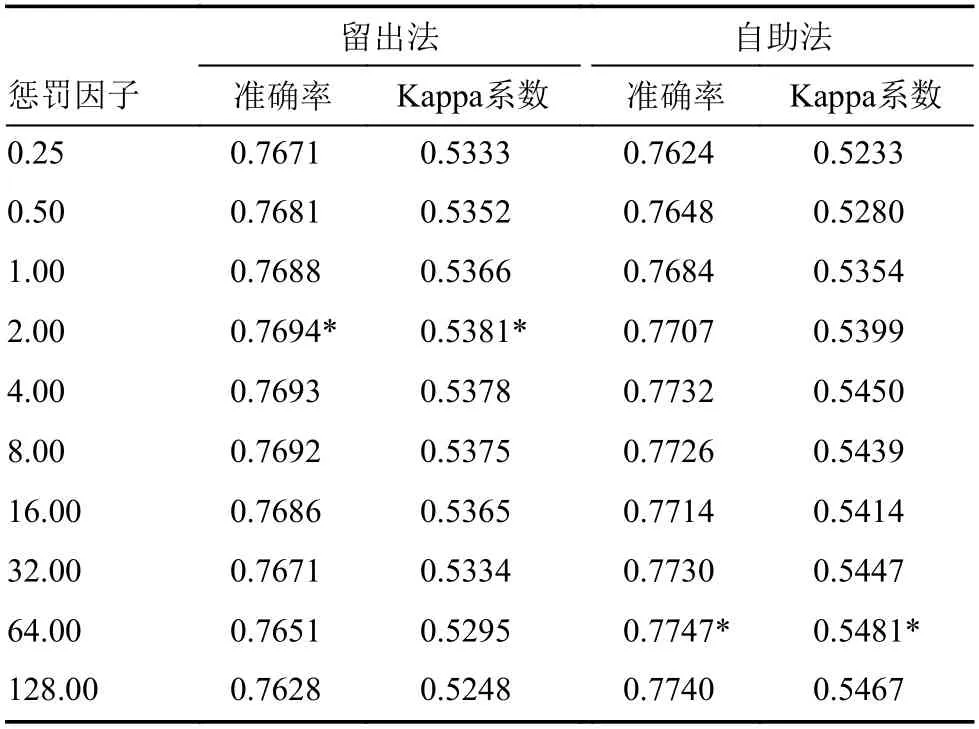
表1 基于留出法和自助法的2015～2018 年黑龙江省夏季逐日降水SVM 统计预报模型的参数调优Table 1 Parameter tuning of the SVM (Support Vector Machine) statistical prediction model of summer daily precipitation in Heilongjiang Province from 2015 to 2018 based on Hold-out and Bootstrap methods

3.3 DT 降水统计预报模型的构建

在训练DT 模型时，追求更高的训练集正确分类的准确率，容易导致建立的决策树结构过于复杂、分支过于繁多，造成过拟合的问题，因此需要对某些分支进行主动删减，简化生成的决策树，以减小过度拟合的风险。代价—复杂度参数（Complexity Parameter，CP）是DT 剪枝的依据。作为控制决策树规模的惩罚因子，CP 参数值越大，决策树的复杂度越小，准确率越低。因此合适的CP 参数值不仅可以解决过拟合的问题，而且可以提高准确率。一般选择准确率最大值对应的CP 参数值对决策树进行剪枝。

通过不断地对比和调试，可以得到不同CP 参数值下拟合模型的统计量。根据表2 容易获悉：基于留出法的DT 模型CP 取值为0.0073 时，模型的准确率和Kappa 系数最大，取值为73.96%和0.4786，因此最优参数为0.0073；基于自助法的DT 模型CP 取值为0.0181 时，模型的准确率和Kappa 系数最大，取值为72.73%和0.4533，因此最优参数为0.0181。

表2 基于留出法和自助法的2015～2018 年黑龙江省夏季逐日降水DT 统计预报模型的参数调优Table 2 Parameter tuning of the DT statistical forecast model of daily precipitation in summer in Heilongjiang Province from 2015 to 2018 based on Hold-out and Bootstrap methods

4 降水统计预报模型的性能分析

基于10 折交叉验证的参数最优模型，通过对BPNN、SVM、DT 3 种降水统计预报模型拟合测试集数据后的准确率、敏感度、特异度进行比较，对降水统计预报模型的泛化性能做出有效估计；计算出3 种降水统计预报模型的ROC 曲线面积和95%置信区间（Confidence Interval，CI），对降水统计预报模型的预报性能进行分析；分别对3 种模型进行ROC 曲线面积的统计假设检验，对降水统计预报模型的预报性能进行比较；选择泛化性能最好的模型，建立该模型下黑龙江省2019 年夏季各站点的降水统计预报模型，并对各站点的预报性能进行空间分布分析。

4.1 降水统计预报模型结果分析

表3 给出的是基于留出法和自助法的3 种降水统计预报模型的准确率、敏感度、特异度性能度量指标值。由表3 可知：基于留出法的BPNN、SVM、DT 降水模型的准确率为75.96%、75.87%、72.14%；敏感度依次为71.76%、71.27%、68.77%；特异度依次为79.64%、79.88%、75.09%。针对准确率和敏感度的比较结果均为BPNN＞SVM＞DT；针对特异度的比较结果为SVM＞BPNN＞DT。基于自助法的BPNN、SVM、DT 降水模型的准确率依次为76.49、76.80、72.68；敏感度依次为72.80、72.47、69.45；特异度依次为79.90、80.81、75.67。针对准确率和特异度的比较结果均为SVM＞BPNN＞DT。综上所述，对于降水发生的预报任务，BPNN的性能最好，而对于降水不发生的预报任务，SVM的性能最好。相比之下，无论基于何种性能度量，DT 的指标值均小于其他两种模型，可认为在黑龙江省夏季降水预报中，DT 的性能最差。除此之外，自助法模拟技术下，3 种预报模型的所有性能度量指标值均比留出法模拟技术高，即自助法估计的性能始终优于留出法。因此，自助法模拟技术能够提高模型的预报性能，客观有效的评价模型的预报效果。

表3 基于留出法和自助法的2015～2018 年黑龙江省夏季逐日降水的3 种统计预报模型的结果Table 3 Results of the three statistical forecast models of daily precipitation in Heilongjiang Province in the summer from 2015 to 2018 based on Hold-out and Bootstrap methods

4.2 降水统计预报模型性能比较检验

不同的评价指标往往反映了不同的任务需求，因此使用不同的性能度量往往会导致不同的评判结果，综合考虑统计预报模型在不同任务需求下的性能高低，或者说一般情况下性能的高低，使用ROC曲线及曲线下面积ROC 曲线面积对模型进行综合评价。图3 为基于留出法和自助法的3 种降水预报模型的ROC 曲线图。其中，红色线代表BPNN，绿色线代表SVM，蓝色线代表DT，灰色线是一条分界线，衡量模型是否拥有预报效果，位于其上代表模型拥有预报价值，位于其下代表模型无预报价值。可以发现，图3a 和图3b 差别甚微，两张图中BPNN 的ROC 曲线与SVM 近乎重合，相比DT 更陡峭，更接近于直线y=1。由此表明，两种统计模拟技术下，模型的性能分析结果具有一致性。

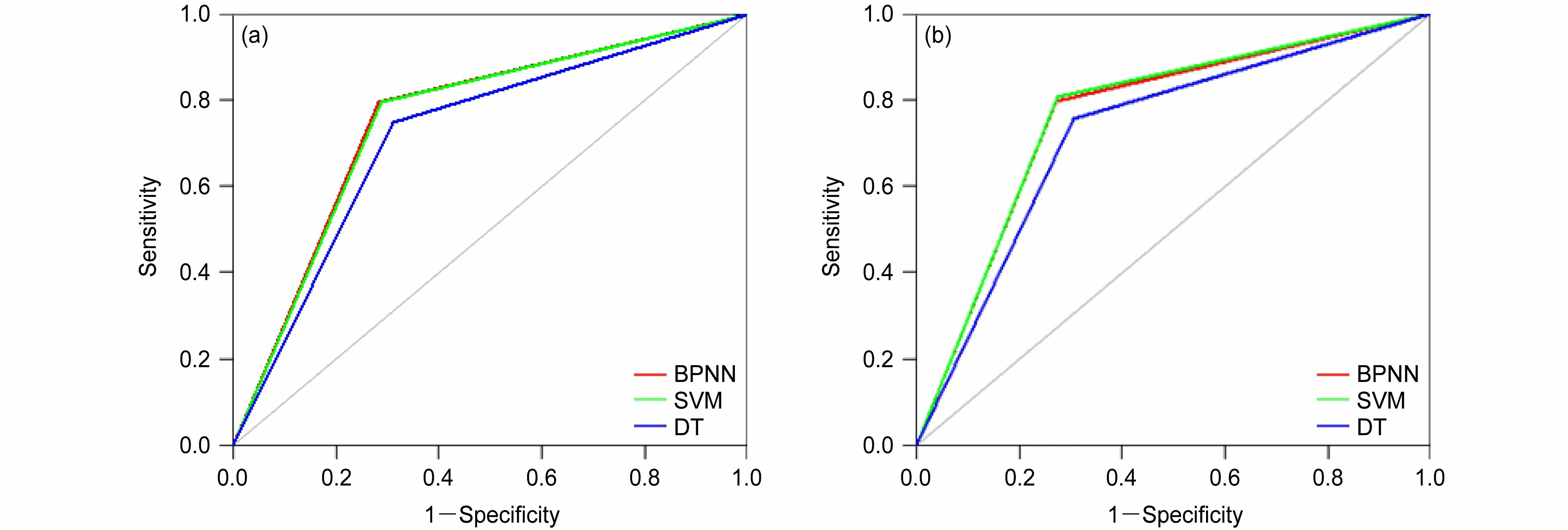
图3 基于（a）留出法和（b）自助法的2015～2018 年黑龙江省夏季逐日降水的3 种统计预报模型的ROC 曲线。灰色线是一条分界线，位于其上代表模拥有预报价值，位于其下代表模型无预报价值Fig. 3 ROC curve of the three statistical forecasting models for the daily summer precipitation in Heilongjiang Province from 2015 to 2018 based on(a) Hold-out and (b) Bootstrap methods. The gray line is a dividing line. Above it, the model provides a forecast value, while below it, the model provides no forecast value

BPNN 和SVM 的曲线发生交叉，难以一般性地断言二者孰优孰劣，使用ROC 曲线面积综合评价指标对3 种模型的性能进行合理比较。ROC 曲线面积为ROC 曲线下面积，是ROC 曲线陡峭程度的量化值，ROC 曲线面积越大，模型的预报性能越好。表4 为基于留出法和自助法3 种模型的ROC 曲线面积和95%置信区间汇总表，基于留出法的ROC 曲线面积按从大到小依次排序为BPNN＞SVM＞DT；基于自助法的ROC 曲线面积按从大到小依次排序为SVM＞BPNN＞DT。

表4 基于留出法和自助法的2015～2018 年黑龙江省夏季逐日降水的3 种统计预报模型的ROC 曲线面积和95%置信区间Table 4 The area under ROC cuvre and 95% confidence interval of three statistical forecasting models for daily summer precipitation in Heilongjiang Province from 2015 to 2018 based on Hold-out and Bootstrap methods

3 种统计预报模型本身具有一定的随机性，仅根据评价指标的数值大小评价模型性能，显然缺乏科学依据。为了对3 种降水预报模型进行客观比较，站在统计学的角度，采用ROC 曲线面积显著性检验方法统计假设检验，对3 种降水统计预报模型的ROC 曲线面积进行统计学差异的检验。根据表5可知：基于留出法的BPNN 与DT 的ROC 曲线面积的P为1.119×10-8，SVM 与DT 的ROC 曲线面积的P为3.801×10-8，均小于0.001，因此认为DT 与BPNN 和SVM 的差异非常显著；而BPNN与SVM 的ROC 曲线面积的P为0.7233，大于0.05，因此认为二者的差异不显著。基于自助法的BPNN与DT 的ROC 曲线面积的P为4.719×10-9，SVM与DT 的ROC 曲线面积的P为2.652×10-11，均小于0.001，因此认为DT 与BPNN 和SVM 的统计学差异非常显著；而BPNN 与SVM 的ROC 曲线面积的P为0.5226，大于0.05，因此认为二者的差异不显著。综上所述，两种统计模拟技术下，3种模型的性能分析结果一致。因此，对于黑龙江2015～2018 年夏季逐日降水的预报，BPNN 和SVM的预报性能差异无统计学意义，二者的预报性能显著优于DT。

表5 基于留出法和自助法的2015～2018 年黑龙江省夏季逐日降水的3 种统计预报模型的ROC 曲线面积统计学差异检验Table 5 The area under ROC cuvre test of three statistical prediction models of summer daily precipitation in Heilongjiang Province from 2015 to 2018 based on Hold-out and Bootstrap methods

4.3 SVM 降水统计预报模型性能空间分布

为了进一步对降水统计预报模型性能空间分布进行分析，依据前两节研究结果，利用自助法、10 折交叉验证方法、SVM 统计学习方法和2019年黑龙江省夏季28 个站点气象资料，基于SVM建立各站点的降水统计预报模型，并从空间分布角度对模型预报性能进行分析。

为了评估基于SVM 的各站点降水统计预报模型的预报性能，图4 给出了该模型下黑龙江省各站点夏季降水的准确率、敏感度、特异度和ROC 曲线面积箱线图。可以看出，4 个评价指标均存在异常站点，准确率的异常值出现在宝清站和孙吴站，ROC 曲线面积的异常值出现在绥芬河站、孙吴站和宝清站，敏感度的异常值出现在宝清站和泰来站，特异度的异常值出现在绥芬河站。4 个指标的中位数分别为84.78%、84.52%、89.68%和82.09%，均高于80%。除了这4 个异常站点外，黑龙江省其他站点的夏季逐日降水预报性能都较好。

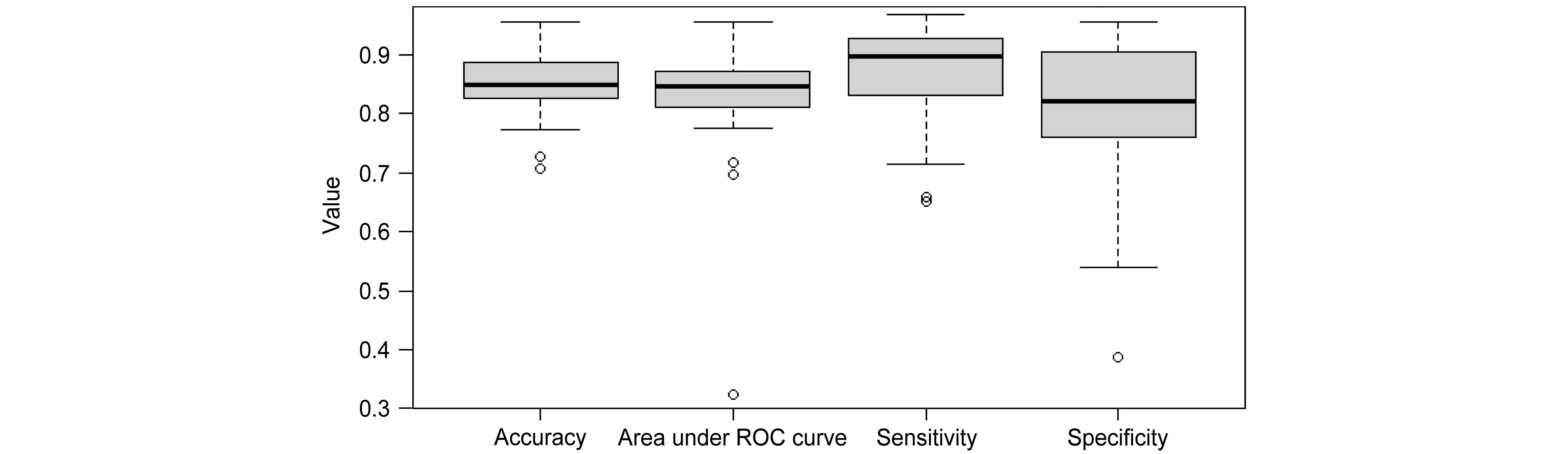
图4 2019 年黑龙江省夏季逐日降水统计预报模型的准确率、ROC 曲线面积、敏感度和特异度箱线图Fig. 4 Accuracy, area under ROC cuvre, sensitivity, and specificity boxplots of daily precipitation statistical prediction models in Heilongjiang Province in 2019

图5 给出了黑龙江省2019 年各站点夏季降水发生频率、逐日降水统计预报模型的准确率、敏感度、特异度和ROC 曲线面积的空间分布情况和变化趋势。从图中可以看出夏季降水频率的高值中心位于黑龙江省张广才岭的绥芬河站和勃利站，降水频率大于61.96%。东南地区的夏季降水频率明显高于西北地区。特别地，松嫩平原的泰来站和大兴安岭的漠河站的夏季降水频率小于0.5，整体呈现由东南向西北递减的趋势。这主要是因为黑龙江省小兴安岭和张广才岭的迎风坡对地形有较好的抬升作用，再加上各种天气系统在此过境，因此形成了降水频率高值区，而松嫩平原由于距离副热带高压较远，并且缺乏地形抬升条件，不易形成降水，因此频率较小。准确率的高值中心位于小兴安岭的伊春市，并以北安站、铁力站和通河站为轴线逐渐向两侧递减，除了宝清站，孙吴站和绥芬河站外，其余站点的准确率均高于80.43%，并且勃利站、佳木斯站、北安站和通河站的准确率均高于90.22%。整体趋势与降水频率一致。敏感度的低值中心较为集中，位于西北部的齐齐哈尔市，东部地区除了牡丹江站和宝清站外，其余站点的敏感度均高于90.57%，西部地区除了齐齐哈尔市的所有站点和大兴安岭的呼玛站外，其余站点的敏感度均高于81.25%，整体呈现由东南向西北递减的趋势。特异度的高值中心位于西北部的齐齐哈尔市，该区域内所有站点的特异度均高于88.99%，特别地，在齐齐哈尔站取最大值95.56%，整体呈现由西北向东南递减的趋势。ROC 曲线面积的分布与准确率的空间分布具有高度一致性，这从一个侧面反映出：当类别数量差异较小时（本文降水和不降水的样本比例约为6:4），准确率完全可以反映模型的整体预报性能。

图5 2019 年黑龙江省各站点夏季逐日降水性能空间分布：（a）降水频率；（b）SVM 的准确率；（c）SVM 的敏感度；（d）SVM 的特异度；（e）SVM 的ROC 曲线面积Fig. 5 Spatial distribution of the summer daily precipitation performance at different stations in Heilongjiang Province in 2019: (a) Precipitation frequency: (b) accuracy of SVM; (c) sensitivity of SVM; (d) specificity of SVM; (e) area under ROC cuvre of SVM

基于以上分析可以发现，SVM 模型对于2019年黑龙江省夏季各站点的逐日降水整体预报效果较好，特别地，黑龙江省东南部的预报性能高于西北部。降水频率与敏感度的空间分布趋势吻合，与特异度的空间分布趋势相反，即SVM 模型在降水频率越高的地区，对于发生降水的预报性能越好，而对于不发生降水的预报性能越差。两个性能度量指标在同一区域的评判结果完全相反，这主要是因为不同的性能度量指标反映的是不同的预报任务需求，不同的任务需求评判依据不一样，结果自然不相同。因此，模型的性能优劣是相对的，一个模型预报性能的评价不仅取决于模型的算法和数据，还取决于模型的预报任务需求和相应的性能度量指标。

5 结论与讨论

本文利用黑龙江省28 个站点的夏季逐日降水资料，分析了2015～2018 年黑龙江省基于不同统计模拟技术和性能度量指标的3 种逐日降水统计预报模型的性能，归纳了2019 年黑龙江省夏季各个站点预报模型性能空间分布特征，并进一步分析了模型性能评估的影响因素，得到如下主要结论：

（1）自助法对于模型预报性能的估计始终优于留出法，但最大相对提升幅度仅为1.2%。这主要是因为自助法虽然避免了训练样本规模不同而导致的估计偏差，但是它的效果在数据量较小，难以划分训练集和测试集时才更为显著。由于本文数据量较大，提升幅度较小也事出有因。

（2）对于2015～2018 年黑龙江省夏季逐日降水预报，BPNN、SVM 和DT 的ROC 曲线面积均高于70%，3 种模型对于黑龙江夏季逐日降水均有较好的预报效果。特别地，BPNN 和SVM 的整体预报性能显著优于DT，而二者的整体预报性能无统计学差异。

（3）针对2019 年黑龙江省夏季各站点逐日降水预报，除了个别站点外，SVM 降水统计预报模型的整体预报性能较好，ROC 曲线面积可高达95.44%。特别地，在降水频率较高的东南部，预报性能较好，而降水频率较低的西北部，预报性能较差。此外，各站点的降水频率与敏感度呈正相关，与特异度呈负相关。可见，SVM 模型在降水多的地区对发生降水的预报性能较好，对不发生降水的预报性能较差，由于黑龙江夏季降水频率差异相对较小，敏感度和特异度的数值差异也较小。

（4）模型的预报性能既与算法和数据有关，又与预报任务需求和性能度量指标有关。因此，模型性能评估需要综合考虑各种因素的影响，才能科学客观的进行性能分析。