基于有限元-统计能量分析混合法座舱噪声特性研究

沈 重，陈忠明

（沈阳飞机设计研究所，沈阳 110035）

座舱噪声水平是衡量飞行器舒适性的一个重要指标，虽然CCAR36部对座舱噪声没有明确的规定，但各航空制造公司为了不影响其产品的商业运营，均对舱内噪声制定了自己的限制性要求。战斗机由于其用途的特殊性，致使对其舱内噪声水平关注度明显不足，在战斗机设计过程中，舱内噪声只要乘员可以忍受、不影响正常无线电通话即可，很少关注对乘员听力及人机功效性能的影响。

随着对人机功效性能的逐步重视，军用飞机座舱噪声问题也逐渐成为飞行设计过程中须要考虑的一项重要指标，国内在座舱噪声预计和控制领域也开展了相应的研究。孙亚飞等[1]对座舱噪声开展了主动控制研究，取得了较好的降噪效果；张霞等[2]对歼击机噪声进行了研究，提出应对歼击机噪声控制加强研究工作；余文斌等[3]研制了有源消声耳罩，其降噪量可达15 dB以上。

本文针对战斗机座舱，基于统计能量法对座舱噪声进行了仿真分析，得到座舱噪声水平，可为座舱声学优化提供理论依据。

1 统计能量分析方法（Statistical Energy Analysis，SEA）

传统的有限元方法和边界元方法在对噪声分析的应用上存在一些明显的局限，主要原因是对于复杂结构，声学分析的频率范围通常要覆盖几十阶模态，在维持一定计算量的前提下，高阶模态模型的计算精度较差；或者，在达到一定精度条件下所需要的计算量过于庞大，以至难于承受。20世纪60年代发展的统计能量分析方法是研究高频宽带随机激励复杂结构的振动与声响应及声传输等问题的有效方法。其不需要求解复杂的数学物理方程，而是用统计的概念研究多元系统间能量的传递和平衡。统计能量分析法是使用统计模态的概念，把振动能量作为描述振动的基本参数，并根据振动波和模态间存在着的内在联系，建立分析声、结构振动和其他不同子系统耦合动力学的方法。统计能量分析法适用于分析含有高频、高模态密度的复杂系统（含声子系统和结构子系统，或只含结构子系统）的耦合动力学问题

统计能量分析的基本原理[4]是将一复杂结构划分成若干子系统，当某个或者某些子系统受到激励时，子系统间将通过边界进行能量交换；这样对每个子系统都能列出一个能量平衡方程，并最终得到一个高阶线性方程组，求解此方程组可得到各子系统的能量，进而由子系统能量得到各个子系统的振动参数，如位移、速度、加速度等。

2 座舱统计能量分析法模型

统计能量法从统计意义上把复杂系统划分为一些简单有限的子系统，其中包括一维梁子系统、二维平板子系统、单曲面子系统、双曲面子系统和圆柱子系统。建立的子系统必须能够清楚地表示出振动能量的输入、存储、损耗和传输的特性。建立子系统的原则如下：

（1）子系统所有模态要有相似的共振模态，并给出SEA参数在频段范围内的平均值；

（2）对系统组件要进行相似模态定义；

（3）在系统的一部分中，不同的模态，比如弯和扭，当它们在共振频段内强耦合时可看作一个模态群，否则应当作两个相互独立的模态群；

（4）子系统的模态密度必须足够高，分析带宽Δω内的模态数目要超过5。

依据上述原则对座舱进行子系统划分，SEA 模型如图1 所示，共34 个结构子系统，其中19 个面单元子系统、11个梁单元子系统、4个声空间子系统。

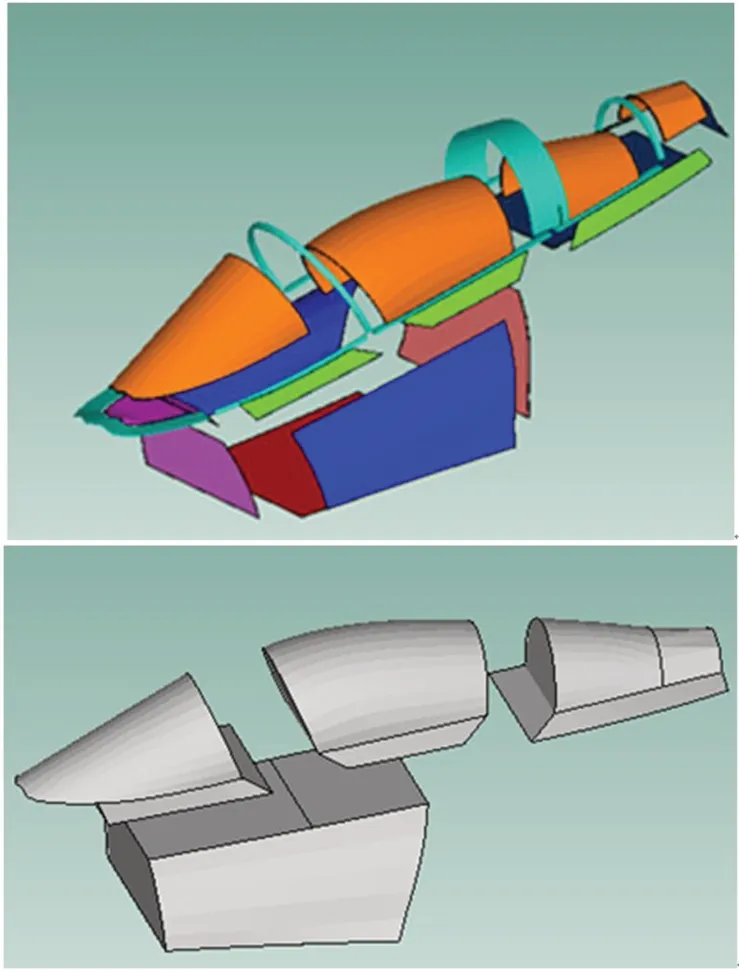
图1 座舱统计能量分析模型

3 统计能量法分析法参数的确定

3.1 模态密度

模态密度类似于热力学中的热容量，它是描述振动系统贮存能量能力大小的物理量[5]，二维平板的模态密度计算式为：

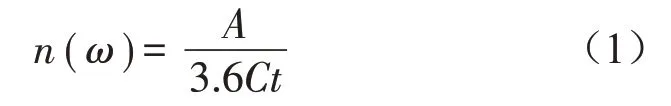
上式中：A为板的面积，C为波速，t为板的厚度。

一维梁的模态密度计算式为：

上式中：l为梁的长度，C为波速。

声场的模态密度计算式为：

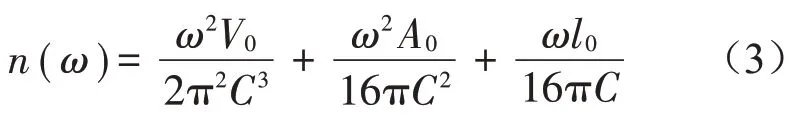
式中：V0为声场体积，A0为表面积，l0为声场棱边总长，C为波速。

利用上述公式，计算各子系统的模态密度，如图2所示。

从图2 可以看出梁子系统在20 Hz～10 000 Hz分析频带内的模态数不满足统计能量法分析要求，且部分板子系统在分析频带内的模态数较低，这会极大地影响分析的准确度。因此，对梁子系统及部分板子系统采用有限元进行重新建模，如图3所示，利用FEA-SEA混合法对座舱噪声进行分析，从而提高分析准确度。

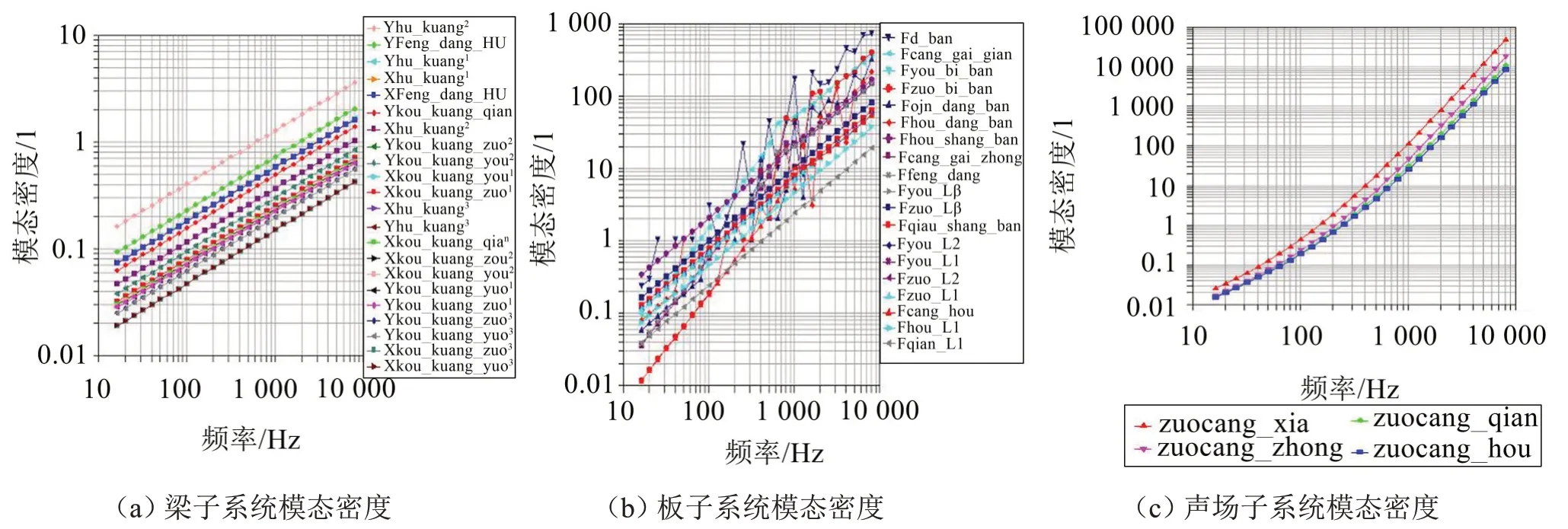
图2 子系统模态密度图

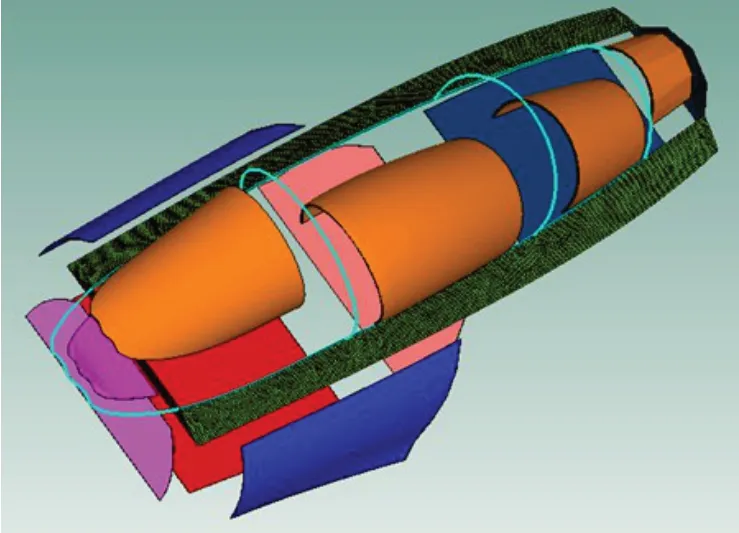
图3 FEA-SEA混合单元座舱模型图

3.2 内损耗因子

内损耗因子的大小主要取决于子系统的阻尼特性。如果阻尼损耗因子小于0.1，不同性质阻尼对响应估算的影响很小，飞机结构大部分采用铝合金材料，座舱盖采用有机玻璃材料，其结构的内损耗因子远小于0.1，因此其结构内损耗因子的取值对本文的分析结构影响较小。本文在分析时，铝合金结构的内损耗因子[6]选取为0.000 1，舱盖结构的内损耗因子[6]选取为0.002。

3.3 耦合损耗因子

耦合损耗因子是统计能量法特有的参数，它表示从一个子系统到另一个子系统的功率流传输特性。子系统间的耦合损耗因子是统计能量法计算时最难确定的参数。可根据连接形式、连接类型和连接角度进行估算，还可根据数值方法进行计算[7]。文献[7]详细地给出了不同子系统间耦合损耗因子的计算方法，本文用VA one软件自动计算得到的耦合损耗因子进行噪声分析。

4 激励参数

4.1 湍流边界层脉动激励

气流作用在结构表面产生的脉动压力由结构几何外形、马赫数和气流作用角度等众多因素决定。根据气流作用角度可将气流作用在结构表面情况大体分为分离和黏附状态[8]，如图4 所示。文献8 详细给出了湍流边界层作用下结构表面脉动压力均方根值及功率谱密度计算方法，本文使用该方法计算湍流边界层产生的脉动压力激励，将其施加于舱盖结构上。

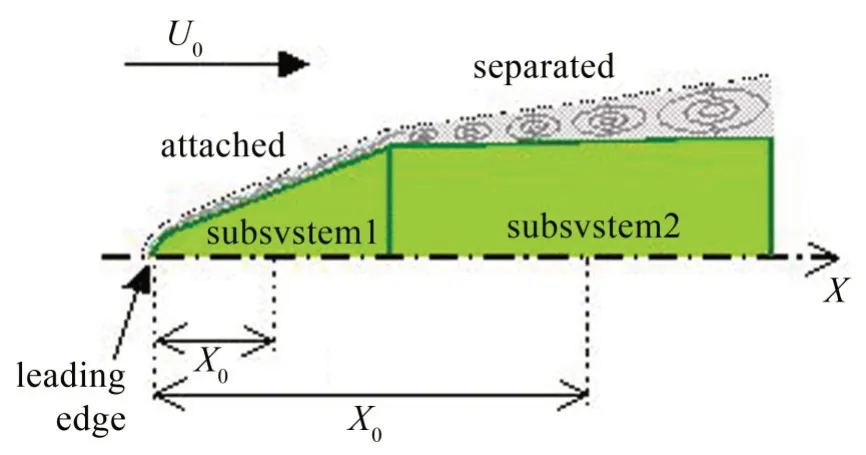
图4 湍流边界层作用示意图

4.2 发动机振动激励

对战斗机而言，发动机直接与机身连接，因此发动机传递到结构上的振动是机体结构的主要振源之一。虽然座舱距发动机与机身连接部位较远，但其振动量值也会对座舱噪声水平产生影响，如忽略的话将影响座舱噪声响应分析结果的准确性。在试飞阶段，对座舱结构进行了振动测试，结构的典型振动加速度曲线如图5 所示，将其施加在座舱结构上用于座舱噪声分析。

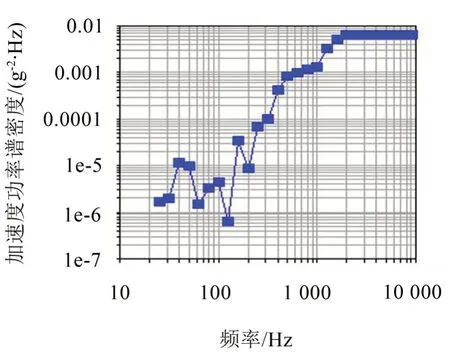
图5 振动加速度功率谱密度曲线图

施加湍流边界层脉动激励与振动加速度激励的分析模型如图6所示。

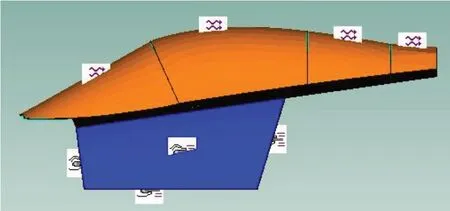
图6 施加激励分析模型图

5 座舱噪声声压级仿真结果分析

在跨音速飞行时，由于气流不稳定，造成座舱噪声水平与亚音速、超音速飞行相比较高。因此，本文选取0.9Ma作为典型状态进行座舱噪声水平分析。统计能量分析不能预示子系统的某个局部位置的精确响应，但能较精确地从统计意义上预示整个子系统的响应级。

基于FEA-SEA 混合单元统计能量分析方法计算得到了座舱各系统噪声频谱图，如图7 所示，表1为座舱各系统的总声压级。从图7 可以看出，座舱后部的噪声水平明显高于座舱前部、中部及后部，这种现象的主要原因是高速气流在座舱盖中部分离，会产生强烈湍流，从而导致声压级较高；座舱前部、中部及下部噪声水平基本相当，总声压级约为114 dB；座舱噪声能量主要集中在1 000 Hz～3 000 Hz中高频上，因此，可以采取在座舱内增加吸声棉的方法对该频段进行降噪处理。

表1 座舱各子系统噪声总声压级列表

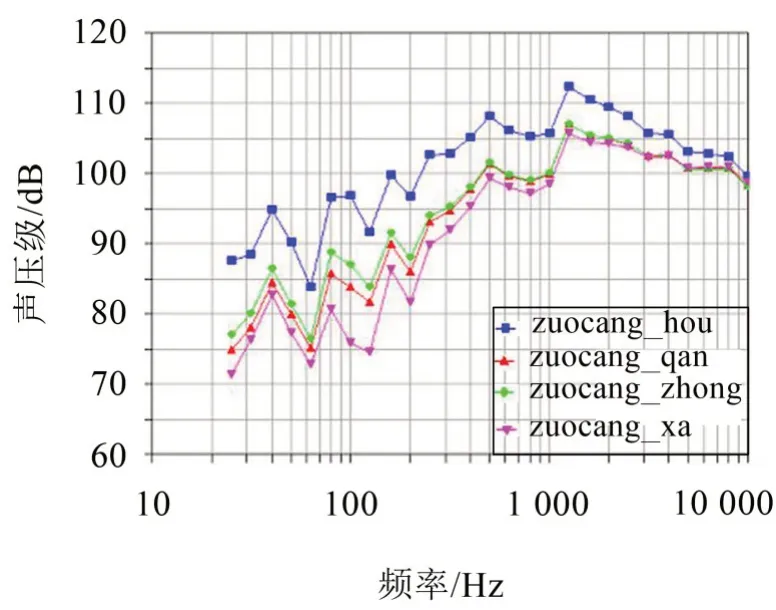
图7 座舱各子系统噪声频谱图

图8为座舱中部噪声仿真分析结果与0.9Ma飞行试验测试结果对比情况，飞行试验测试结果显示，飞行员耳部附近噪声总声压级约为116.3 dB，仿真结果与其仅相差2 dB，虽然在个别频率点上，仿真结果与飞行试验结果相差较大。但在工程上，基于统计能量法的座舱噪声仿真能够达到预计座舱噪声、指导座舱噪声水平优化的目的。

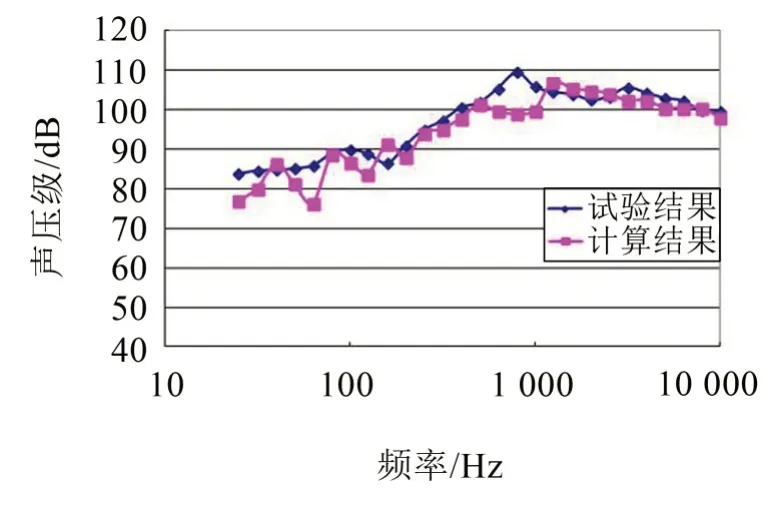
图8 座舱各子系统噪声频谱图

6 结语

传统的有限元方法、边界元法在计算噪声时，随着计算频率的提高，网格需要逐渐加密，这样势必造成计算规模的急剧增大，计算效率大大降低。统计能量法以子结构的模式进行建模，其模型规模与有限元、边界元相比较小，计算效率高，在处理高频问题时更加简便实用。

本文通过基于FEA-SEA 混合单元统计能量法对战斗机座舱噪声进行了建模及仿真分析，并定量得到了座舱的噪声水平，仿真分析结果与飞行试验测试结果相差仅为2 dB，表明该方法可为座舱噪声水平预计及座舱噪声水平优化提供仿真依据。