风电场代表年订正方法研究

王守峰，戚振亚，许卫东

(山东电力工程咨询院有限公司，山东 济南 250013)

1 引言

受化石能源资源日趋枯竭、环境保护等的驱动，自20世纪70年代中期以来，世界主要发达国家和一些发展中国家都开始重视风能的开发利用。国际上风能开发利用的主要形式是风力发电[1]。我国风能资源十分丰富，开发前景广阔，风力发电事业正在蓬勃发展[2]。

建设风电场最基本的条件是要有能量丰富、风向稳定的风能资源，风电场选址时应尽量选择风能资源丰富的地点。所以，对风电场风能资源的评估是整个风电场建设、运行的重要环节，是风电项目的根本，对风能资源的正确评估也是风电场建设取得良好经济效益的关键[3～5]。在风资源评估[6～10]中，代表年计算的目的是通过风场附近的气象站近30年年平均风速的变化规律及风场与气象站实测风速相关关系,分析计算出一套能够反映风电场今后20年运行期间平均水平的代表年的风速系列、计算出风电场今后运行20年的平均发电量及上网电价[3]。本研究将水文中常用的频率分析方法引入到代表年风速订正中，并于传统方法进行对比，以期为代表年风速计算提供新的思路。

2 常规方法

根据《风电场风能资源评估方法》[11]中的规定，将风场短期测风数据订正为代表年风况数据的方法如下。

(1)作风场测站与对应年份的长期测站各风向象限的风速相关曲线。某一风向象限内风速相关曲线的具体做法是：建一直角坐标系，横坐标轴为长期测站风速，纵坐标轴为风场测站的风速。取风场测站在该象限内的某一风速值(某一风速值在一个风向象限内一般有许多个，分别出现在不同时刻)为纵坐标，找出长期测站对应时刻的风速值(这些风速值不一定相同，风向也不一定与风场测站相对应)，求其平均值作为横坐标即可定出相关曲线的一个点。对风场测站在该象限内的其余每一个风速重复上述过程，就可作出这一象限内的风速相关曲线。对其余各象限重复上述过程，可获得16个风场测站与长期测站的风速相关曲线。

(2)对每个风速相关曲线，在横坐标轴上表明长期测站多年的年平均风速，以及与风场测站观测同期的长期测站的年平均风速，然后在纵坐标轴上找到对应的风场测站的两个风速值，并求出这两个风速值得代数差值(共有16个代数差值)。

(3)风场测站数据的各个风向象限内的每个风速都加上对应的风速代数差值，即可获得订正后的风场测站风速风向资料。

3 Copula函数

3.1 概述

Copula是一个拉丁词，意思是“联结，联合”，适用于非线性相关性的度量，可以描述变量间非线性、非对称的相关关系。自从1959年Sklar[13]提出了Copula函数的定义后，其就被广泛应用于统计文献中，在各个领域中得到迅速地应用，金融、水文[13～15]等领域均得到了广泛应用，然而其在风速订正方面的应用还未见应用。Gumbel-Hougaard 是一种常用的Copula函数，由于其构造简单且易于计算，在水文等方面应用广泛，其形式如下：

C(u,v)=exp(-((-lnu)θ+(-lnu)θ)1/θ，θ∈[1，+∞]

(1)

式(1)中φ(t)=(-lnt)θ,τ=1-θ-1。τ为X和Y的Kendall秩相关系数。

3.2 条件分布

设随机变量X和Y的分布函数分别为Fx(x)和FY(y)，则给定Y=y情况下，X的条件分布函数可以用下式表示：

F(X≤x|Y=y)=Cθ(u|V=v)

3.3 代表年风速计算

将气象站30年风速分布函数定义为,测风塔测风年风速分布函数定义为,则在气象站风速分别为测风年风速与平均风速情况下,求得2个条件分布,相同频率存在2个风速，其差值即为测风年风速与代表年风速的差值。

4 实例应用

以山东省某县风电场为例，为了合理有效的开发风电场，业主在风电场安装了一台70 m高的测风塔进行测风工作，分别在70 m、50 m、10 m高度各安装了一个风速仪，并在70 m、10 m高度各安装了一个风向仪，测风仪器采用美国NRG公司制造的Symphonies测风设备，已收集一年多的现场实测数据。距离风电场最近的气象站位于风电场西南约33 km，气象站最近30年年平均风速见图1。

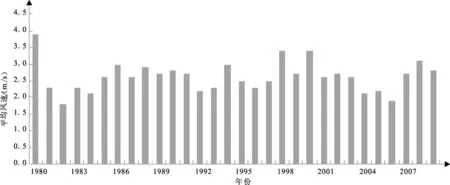
图1 某县近30年年平均风速

4.1 常规方法局限性

气象站近30年平均风速为2.6 m/s，气象站实测年风速为2.9 m/s，所以本风电场实测时段为大风年，根据现场的测风资料与气象站同期的风速、风向小时记录进行相关分析，合理推算风电场代表年的风能要素。按照《风电场风能资源评估方法》中的方法，计算得到风电场70 m处风速与气象站风速各个扇区相关性见表1。

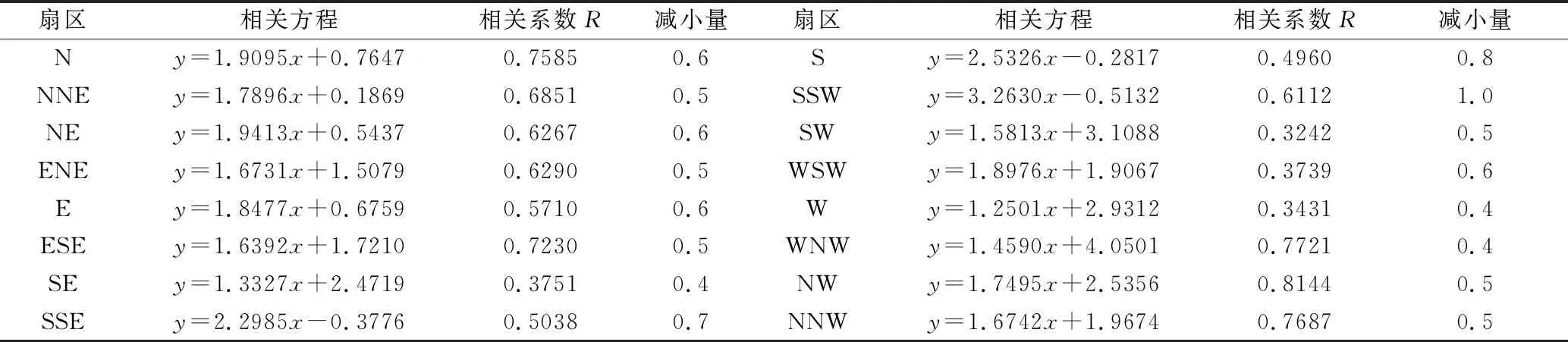
表1 各扇区相关分析结果

由表1可知，仅有 NW这个扇区的相关系数较好，在0.8 以上，可以直接采用相关方程进行订正，而SE、S、SW、WSW 4个扇区的相关系数极差，均在0.5以下，若用此方法计算，得出的订正风速误差较大。又因为测风年为大风年，比平风年高出约0.3 m/s，16个扇区的一次项系数均大于1，特别是SSW一次项系数为3.26，相当于每个SSW风向的风速均减去3.26×0.3=1 m/s，也就是说若测风年风速在0.9 m/s以下，得出的代表年风速为负，这明显是不合乎规律的。

4.2 Copula方法

采用测风年气象站与测风塔同期数据计算kendall 为0.311，θ=1.45，测风塔与气象站的累积分布采用Weibull分布，二者累积分布见图2。

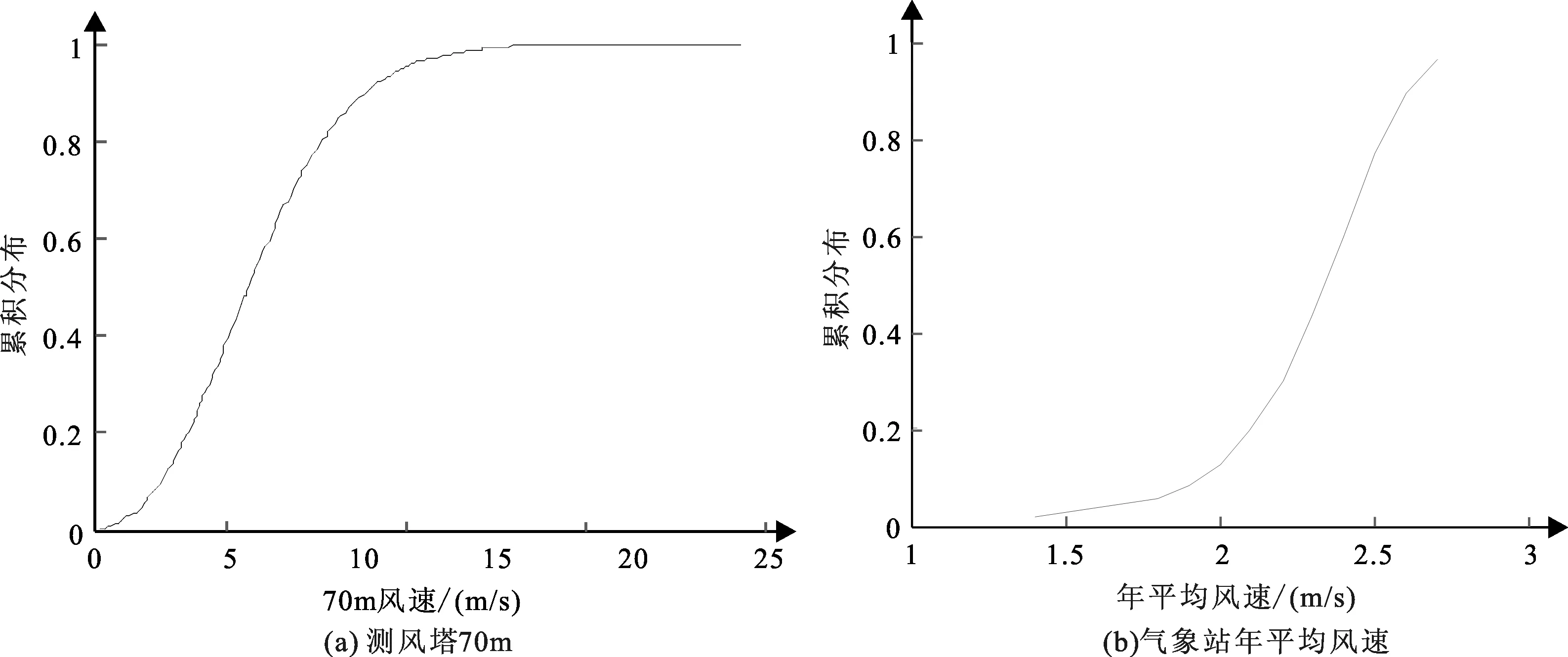
图2 测风塔与气象站风速累积分布

测风年气象站年平均风速为2.6 m/s时，其累计分布概率为0.482，当气象站平均风速为2.9 m/s时，其累计分布概率为0.694。采用3.2节中公式计算条件分布，见图3。图3中，相同的累积分布概率下有两个对应的风速，其差值即为测风年风速与代表年风速差值，由此计算得到代表年风速。

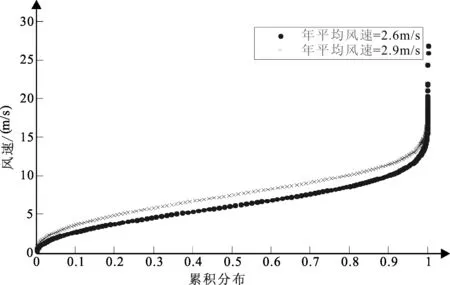
图3 测风塔实测年与代表年风速累积分布

4.2 结果比较

两种方法计算得到的代表年月平均风速及风功率密度见图4。该风场由常规方法计算得到平均风速为6.1 m/s，风功率密度为276 W/m2，采用Copula方法计算的平均风速为5.9 m/s，风功率密度为251 W/m2。

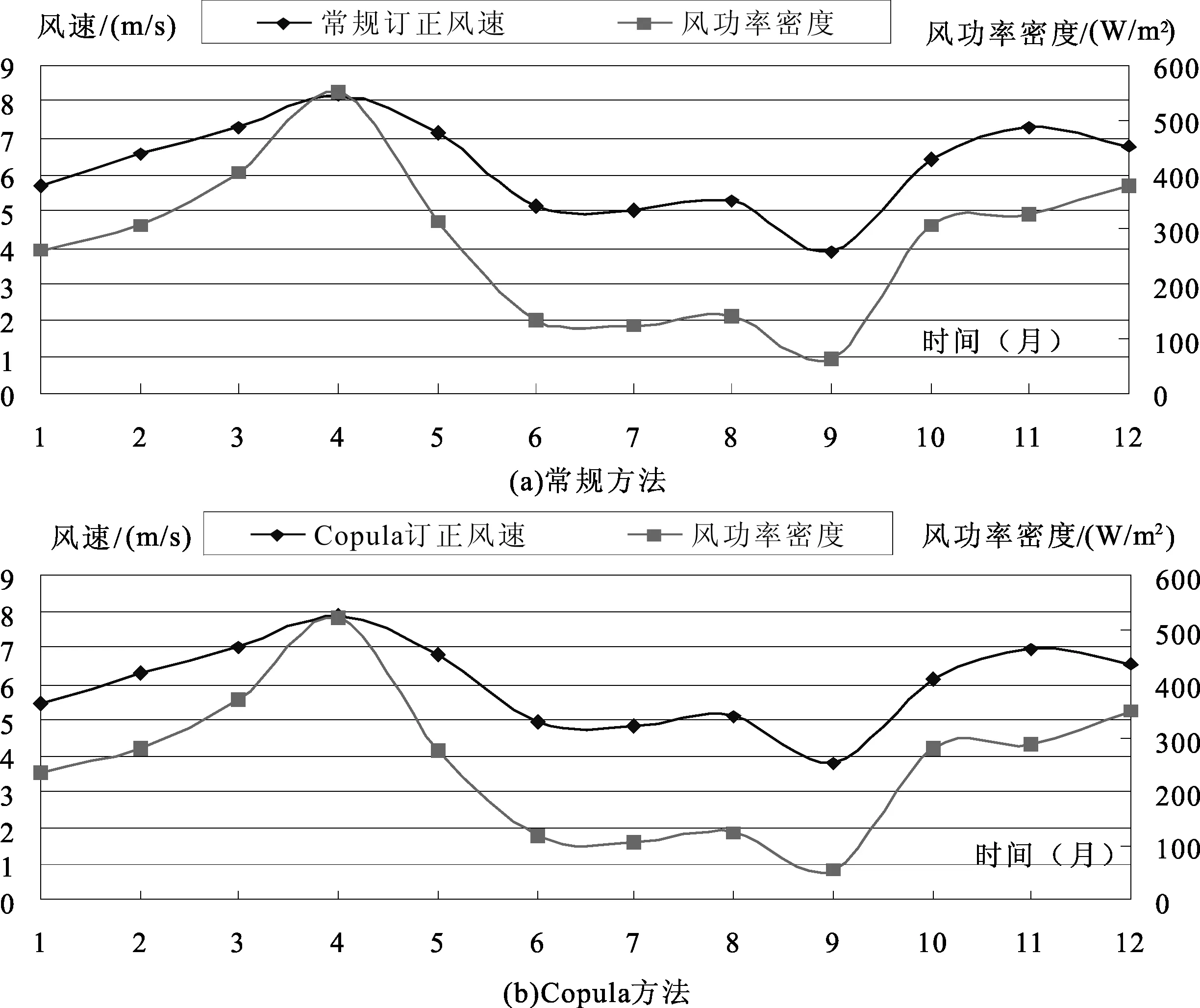
图4 2种方法计算得到代表年月平均风速及风功率密度

5 结论

本文尝试将水文中常用的频率分析代入到代表年风速计算中，得到结论如下：

(1)采用本方法计算结果与常规方法计算结果相差不大，可以应用于风电场代表年风速计算中。

(2)本方法避免了常规算法中相关性差等原因带来的误差，我国正在大力发展海上风电，风电场与气象站的相关性相对陆上风电更差，在此情况下，本文阐述的方法更具有一定优越性。