压力袜压力与位移随着装时间变化的有限元模拟

郑玉婕, 覃 蕊

(青岛大学 纺织服装学院,青岛 266071)

压力袜是日常生活中应用非常广泛的服饰之一[1-3]。在穿着压力袜的过程中,压力袜的功能与着装压力舒适性有着密切联系[4]。目前,关于压力袜的研究大多集中于足踝部压力研究,对于袜口处压力研究较少。袜口是影响压力袜舒适性和功能性的重要部位,压力过小袜口处容易滑脱,压力过大会使穿着者产生不适感,同时给肌体带来负面影响,甚至产生器官与组织病变[5]。因此,压力袜的袜口处应具有适宜的压力分布趋势及压力范围。

对于压感舒适性的评价,传统方法是直接测量人体受压部位压力数据,再结合主观评价进行综合测评[6]。该方法虽然操作简单,但由于受到人的生理和心理因素的影响,容易使实验结果产生偏差[7]。Verillo[8]指出,在理想状态下,低于1 μm的体表位移就能有效引起压感的产生。该结果表明,人体由于压力而产生的内向位移是压感舒适性评价的有效指标。压力袜袜口对人体施压,人体会产生相应的内向位移,不同部位的位移存在差异。同时,随着着装时间的延长,袜口处人体所受压力及位移也呈现不断变化的趋势。深入探讨人体穿着紧身服装过程中压力与位移之间的关系,对于压感舒适性评价及服装的结构优化改良具有一定的参考意义。

本研究以压力短袜为研究对象,通过非接触式三维人体扫描获取袜口处人体腿截面形态,针对压力短袜袜口处存在的压力过大导致不舒适感或压力过小产生的易滑脱等压力分布不合理现象,结合压力袜的着装时间,将着装过程分为6个时间段(瞬时,1、2、4、8、12 h),应用ANSYS有限元软件模拟6个时间段袜口处人体腿截面压力与位移分布趋势。通过曲线拟合,得到6个时间段压力、位移与对应角度的函数关系。即:当人体处于服装压力状态时,在已知压力值的前提下,可通过函数方程计算人体对应的位移值,进而为压感舒适性评价提供数据支撑。该方法为压力袜袜口处的压感舒适性研究及优化设计提供了理论参考,同时可应用于其他类型的紧身服装。

1 压力袜袜口处人体腿截面曲线的确立

1.1 非接触式三维人体扫描

准确的人体形态结构是进行人体压力及位移形变研究的基础,基于此,本研究通过非接触三维人体扫描获取压力袜袜口处人体腿截面形态结构。

通常压力短袜袜口位置为人体内侧脚踝点水平向上5～6 cm处[9],而5 cm和6 cm处截面大小及形状基本相同,本研究将6 cm处定义为袜口截面位置。

1.1.1 实验对象

选取年龄在20～25岁标准体型的健康男性大学生50人。

1.1.2 实验对象选取原则

参照GB 10000—1988《中国成年人人体尺寸》国家标准,实验对象的平均身高和体重与95%的标准中统计数据相似[10]。

1.1.3 实验要求

受试者赤裸腿部站在TecMath非接触式三维人体测量仪上,通过三维人体扫描,把50位受试者内侧脚踝凸出点水平向上6 cm处截面形态扫描并截取出来。图1为随机选取的袜口处腿截面扫描曲线。

图1 袜口处人体腿截面曲线Fig.1 Leg cross section of the top part of socks

1.2 袜口处腿截面形态的获取

剔除不符合标准的截面曲线,本研究选取其中的40个截面进行处理。将40条曲线同心叠加,圆心为截取截面曲线时三维扫描系统自动定义的圆心。用Matlab软件按照直角坐标系每5°为一点等分,分别确定40个截面曲线中72个点的坐标,再将40个截面坐标的各对应点分别取平均值,即得到平均腿部截面图及各点坐标值(图2)。

图2 袜口处腿截面形态Fig.2 Shape of the leg cross section at the top part of socks

2 实验样品的选取及压力测试

2.1 实验样品的选取

考虑到市面上常用压力短袜的面料成分组成,本研究选取了6款常见的压力短袜作为实验样品,并将6款样本根据面料成分划分为两组,袜口部位具体参数如表1所示。

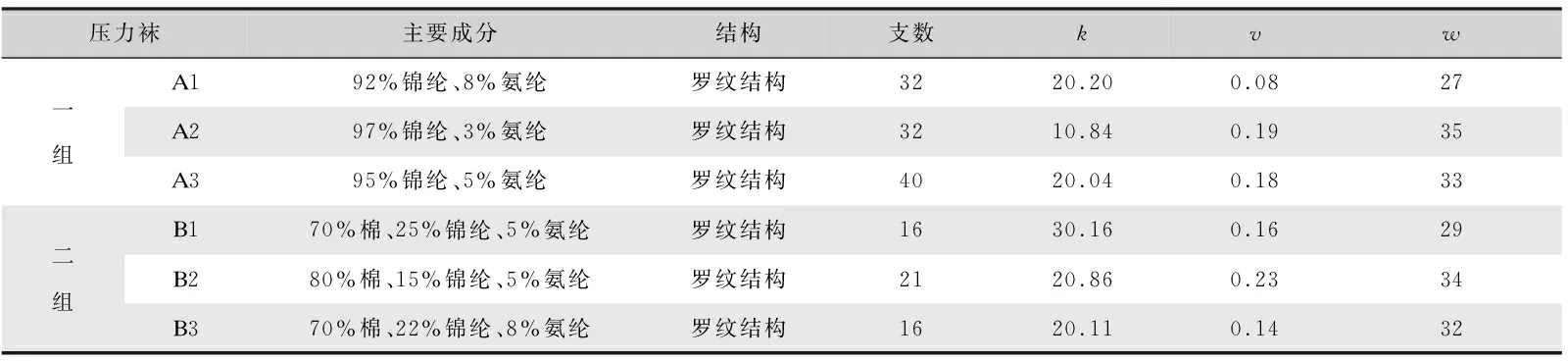
表1 6款实验用压力短袜性能参数Tab.1 Detailed parameters of six experimental socks

其中,A1、A2、A3主成分为锦纶,B1、B2、B3为棉;k(N/m)为袜口弹性系数,v为袜口材料泊松比,w(mm)为原始袜口宽。

2.2 压力测试

本研究使用AMI3037-5S气囊式服装压力测量装置(日本AMI公司),测量受试者穿着6款实验用压力袜时袜口处72点压力值。

通常情况下,人一天中连续穿着压力袜的时间不超过12 h。基于此,本研究定义连续穿着压力袜的最长时长为12 h,并将着装时间划分为6个时间点:瞬时压力,1、2、4、8、12 h,通过压力测试分别得到6款压力袜袜口处72点压力数据。

本研究以A1为例,压力数据如图3所示。

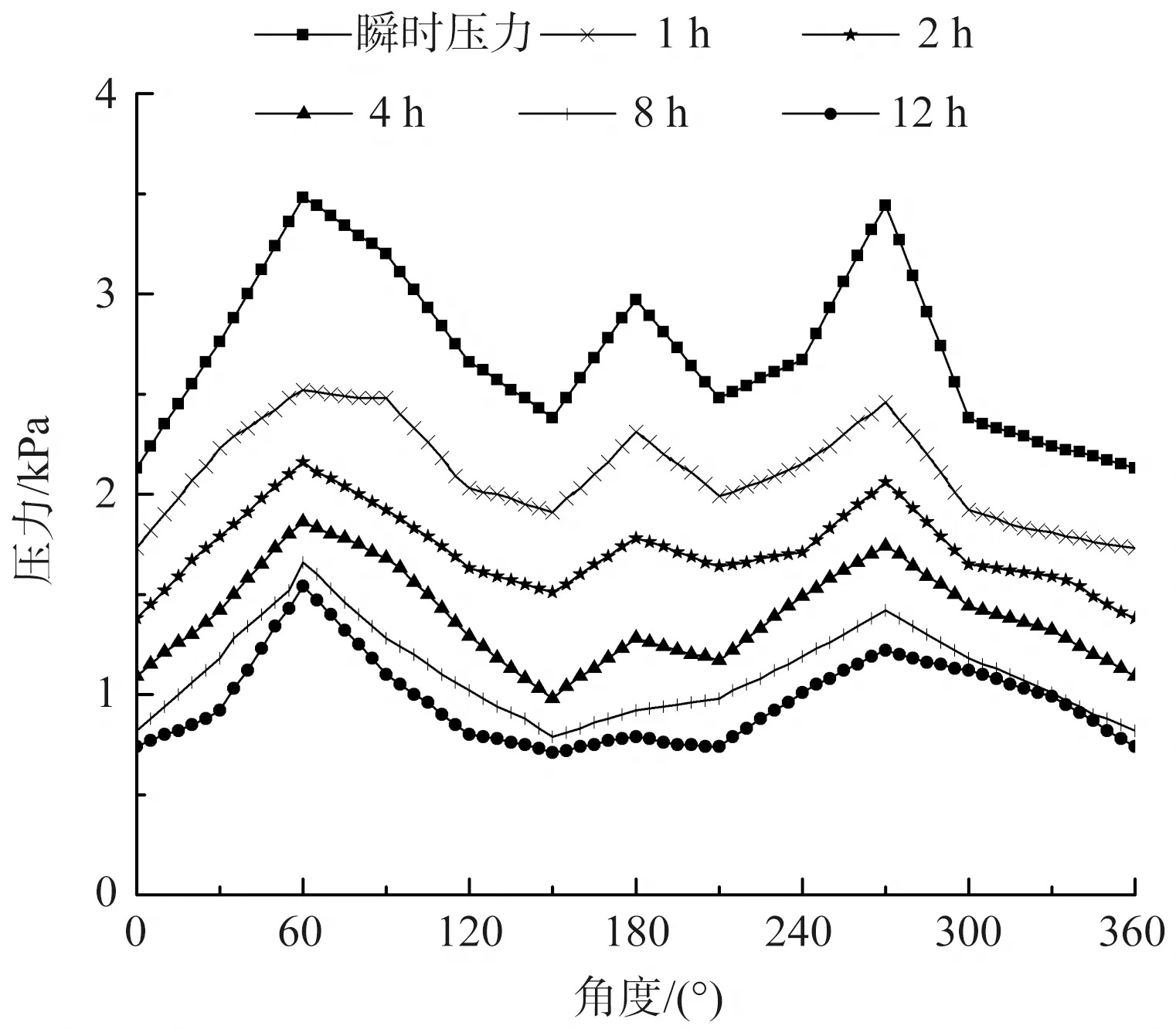
图3 不同时间段压力值(A1)Fig.3 Pressure values in different periods (A1)

由图3可见,袜口处人体腿截面上所有点的压力值随着着装时间的延长均呈现递减趋势。在着装过程中,60°和270°位置压力较大,0°位置压力较小。在瞬时压力中,270°压力值为3.44 kPa,0°压力值2.73 kPa。穿着压力袜1 h后,270°压力值下降为2.46 kPa、下降幅度28.49%,0°压力值1.73 kPa、下降幅度18.78%。可见,在穿着压力袜1 h内,腿截面上原始压力越大的位置,压力数值随着着装时间的延长下降越明显。穿着12 h后,270°压力值下降为1.22 kPa、下降幅度64.53%,0°压力值0.74 kPa、下降幅度65.26%,表明随着着装时间的延长,压力下降幅度趋于平衡。同时,随着着装时间的延长,压力值的下降幅度越来越小,着装后8 h和12 h的压力数据已基本近似。因此可以近似地认为,着装8 h后,袜口处截面上各点压力值基本达到平衡,不同点的压力数值差距逐渐缩小。

3 袜口处腿截面有限元模型的构建

人体小腿截面主要由皮肤、软组织(肌肉、血管、神经)、胫骨和腓骨组成[11],袜口处人体腿部皮肤厚度约为1.5 mm[12]。根据非接触式三维人体扫描及人体小腿处内部结构,本研究构建袜口处人体腿截面有限元模型,如图4所示。

图4 袜口处截面有限元模型Fig.4 FE model of leg cross section of the top part of socks

本研究将人体视为弹性体,腿截面与压力袜间的接触为弹性接触。假设袜口处人体皮肤、软组织及骨骼均为各向同性均匀的线弹性材料,分别设置三种材料的单元类型、弹性模量和泊松比,详细参数如表2所示。

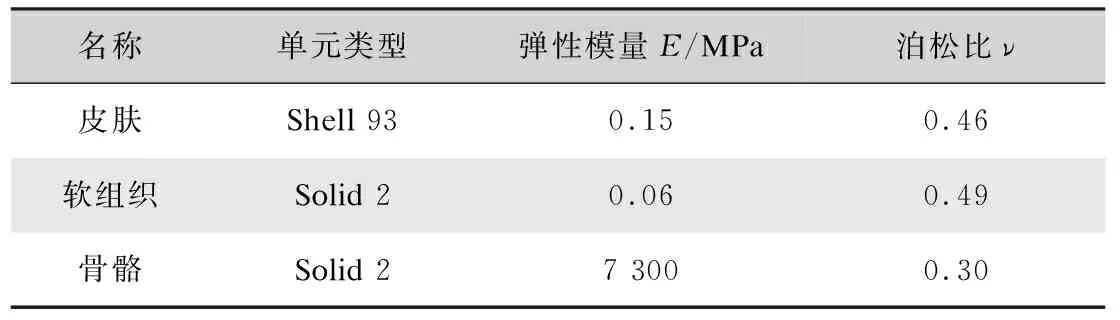
表2 有限元模型的单元类型及材料参数Tab.2 Element type and material parameters of FE model

对袜口处腿截面进行二维三角形网格划分,同时施加压力载荷。骨骼为人体腿截面中最硬的部位,当穿着压力袜后,可以近似地认为胫骨和腓骨在受压后不发生位移。基于此,本研究将胫骨和腓骨X、Y方向位移均为0作为模型的边界条件。

4 着装后腿截面位移的有限元模拟

4.1 袜口处腿截面受压后位移模拟

在ANSYS有限元软件中导入腿截面压力值作为压力载荷,通过求解和后处理,可得到6款压力袜袜口处腿截面位移分布云图。本研究以穿着实验用样品A1一小时为例,位移分布云图如图5所示。

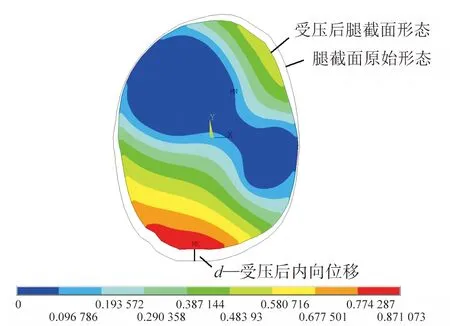
图5 着装1 h后位移分布云图(A1)Fig.5 Displacement distribution cloud chart of leg cross section after 1h (A1)

图5中,不同颜色代表不同的位移大小,下面的颜色带从左到右表示数值依次增加。

4.2 位移随着装时间变化趋势分析

通过有限元模拟,可得到6款实验用压力袜在6个时间段72点各自位移。本研究以A1为例,位移随时间变化数据如图6所示。

图6 位移随着装时间变化曲线(A1)Fig.6 Graph of the displacement values with time (A1)

由图6可见,随着着装时间的延长,腿截面上各点位移均呈递增趋势,且6个时段的位移分布规律基本近似。270°位置为位移最大点,0°位置为位移最小点。在最开始的1 h内,位移的增长幅度最大,约为总体增长幅度的1/3;4 h后,位移增长幅度基本达到整体增长幅度的1/2;而后随着时间的延长,增长幅度越来越小。在穿着压力袜12 h后,位移最大点由原始状态的1.178 mm增至4.44 mm,增长了3.77倍,位移最小点处由原始状态的0.11 mm增至0.41 mm,增长了3.73倍,且同一时段的位移最大值约为位移最小值的2倍。

4.3 袜口处腿截面压力与位移函数关系

当人体受到服装压力时,压力与体表产生的内向位移之间的关系是评价压力舒适性及对紧身服装进行优化设计的关键。为了探讨压力袜整个着装过程中压力与位移间的函数关系,本研究构建了“压力/位移—角度”函数曲线,如图7所示。

由图7可见,6组曲线几乎呈现出相同的变化趋势,最高点约出现在350°位置,最低点约出现在255°位置。曲线分布的总体趋势为[50°,135°]和[255°,350°],数值呈现递增趋势,而[0°,50°][135°,255°]和[350°,360°]递减。从图7还可以看出,无论穿着何种类型的压力袜,且无论着装时长如何,相应位置的“压力/位移—角度”函数关系基本保持不变。该结论为确定压力袜袜口处压力舒适范围提供了可能,也为人体体表位移数据的获取提供了参考依据。

图7 着装过程中“压力/位移—角度”函数曲线Fig.7 Functional curve between pressure/displacement ratio and angle in whole wearing process

为了更加准确地对函数曲线进行拟合,本研究根据曲线趋势对函数曲线进行了转换,角度由[0°,360°]转换为[-10°,350°],如图8所示。

图8 “压力/位移—角度”函数曲线角度转换Fig.8 Conversion curve of pressure/displacement ratio and angle functional curves

根据曲线分布趋势,本研究将函数曲线分为两个区域,分别为[-10°,135°](第一部分)和[135°,350°](第二部分)。通过Origin软件分别拟合两条“压力/位移—角度”二次曲线,拟合曲线及方程如图9所示。

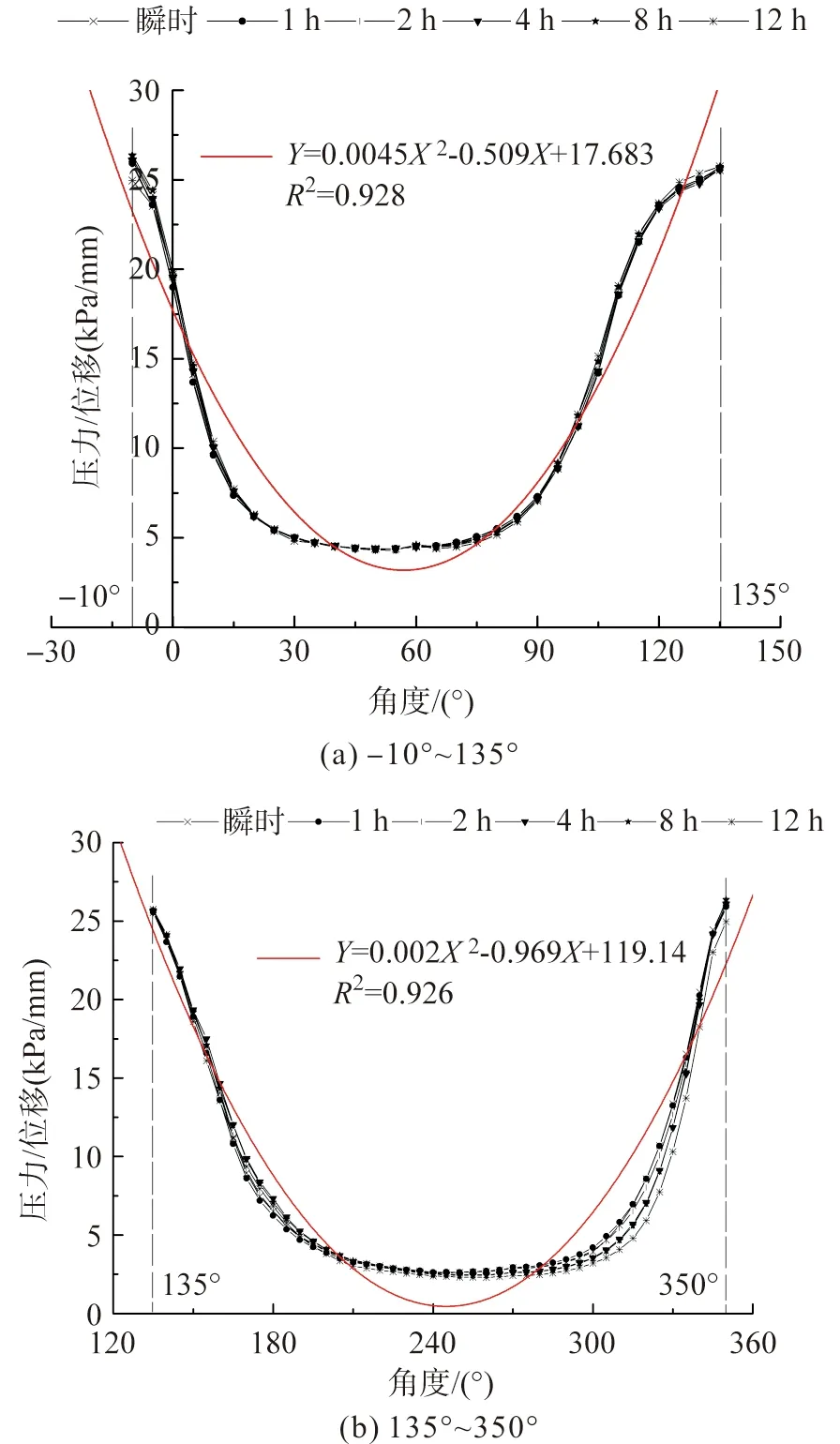
图9 “压力/位移—角度”二次曲线拟合方程Fig.9 Fitting curve of functional relationship between pressure/displacement ratio and angle

在图9中,角度为自变量,“压力/位移”为因变量,拟合曲线为二次方程。拟合曲线方程式及拟合度如表3所示。

表3 拟合曲线方程Tab.3 Fitting curve equations

表3中,两条拟合曲线的拟合度(R2)均在0.92以上,显示拟合度良好。根据拟合曲线方程,可以获取人体位移数据及任意点压力与位移之间的关系。由外部压力产生的垂直于人体体表的内向位移是评价紧身服装压力舒适性的关键指标。但是,由于紧身服装对人体产生的压力有限,因此位移形变通常较小,并且难以使用常规的物理方法获取较为准确的人体位移值[13-15]。利用本研究获得的拟合曲线方程,想要获取人体腿截面上任意点的位移数据,只需要应用压力测试系统测量出该点压力值,将压力值和角度值代入文中求得的二次方程,即可求出该点对应的位移值。

4.4 袜口处腿截面面积缩量分布趋势

人体体表面积缩量是评价紧身服装压力程度的重要指标。根据腿截面面积缩量的分布趋势,在袜子设计过程中,可以将袜口设计为松紧不同的区域,以满足人体的着装舒适性需求。为了获取人体着装后腿截面的面积缩量分布情况,本研究将腿截面上72点中的每四个相邻点构成一个不规则四边形。假设四个相邻点的坐标值为Mn(Xn,Yn)、Mn+1(Xn+1,Yn+1)、Mn′(Xn,Yn)、Mn+1′(Xn+1,Yn+1),该四边形为面积Sn,可以近似地认为Sn的面积等于袜口处腿截面不规则四边形面积Sn′(图10)。

(1)

为了更加准确地判断压力作用下腿截面面积缩量的分布趋势,本研究将袜口处腿截面按照每30°为一个区域等分为12个区域,[0°,30°]为区域1,[30°,60°]为区域2,……,以此类推。依据式(1)分别计算12个区域在不同着装时间段(瞬时,1、2、4、8、12 h)的面积缩量数据,如图11所示(以A1为例)。

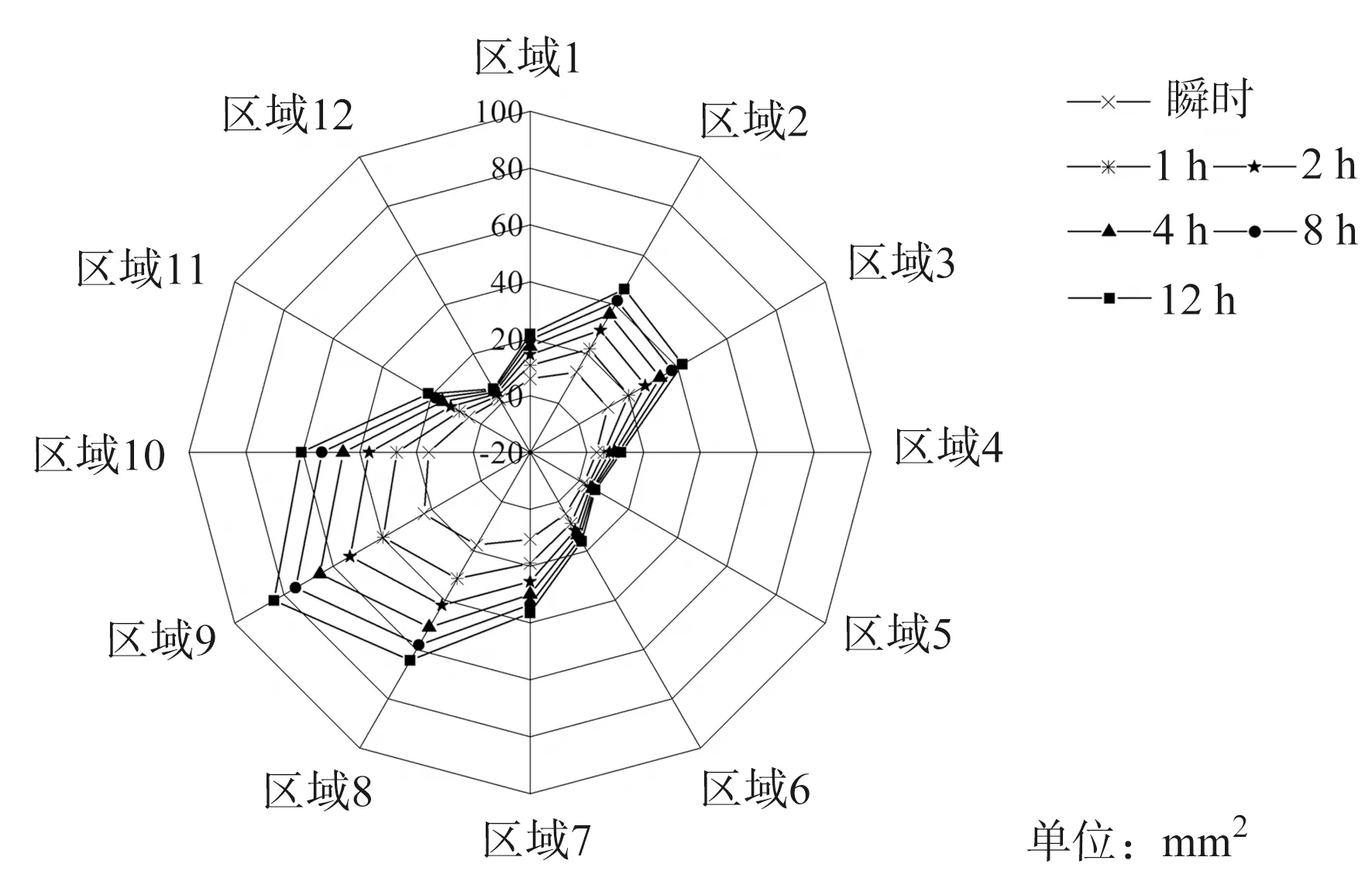
图11 腿截面6个时间段面积缩量(A1)Fig.11 Area shrinkage mass of the lower leg at six periods of time (A1)

由图11可见,12个区域的面积缩量均随着装时间的延长呈现增长趋势。在6个时间段内,区域9在整个着装时间内面积缩量最大,区域5最小,区域12与区域5几乎相同。区域9的面积缩量约为区域5和区域12的15倍。穿着压力袜12 h后,区域9面积缩量增加3.63倍,区域5和区域12约增加3.48倍。由于区域5和12位置有胫骨和腓骨,软组织层较薄,在一段时间的压力作用下,腿截面位移达到平衡。因此,随着着装时间的延长,区域5和区域12的面积缩量增加略小于其他区域。另一方面,在软组织层较厚的区域9中,当其他参数相同时,腿截面位移变化较大。

在压力袜的设计过程中,可以根据面积缩量的分布趋势,结合主观压力舒适性评价,将袜口设计为松紧不同的区域,以满足人体的着装舒适性需求,该结论为压力袜袜口优化设计提供了参考。

5 结 论

紧身服装对人体体表产生的位移是评价压感舒适性和进行服装结构优化的重要指标。通常情况下,紧身服装产生的人体形变较小,并且很难通过常规物理方法获取位移数据。本研究提供了一种准确、简单可行的方法获取人体穿着紧身服装后的位移数据。

1) 以弹性压力袜为研究对象,在已知人体小腿处各部位的相关物理参数及压力袜口对人体腿部施加的部分点压力数据的前提下,将压力袜的着装过程分为6个时间段(瞬时,1、2、4、8、12 h),通过非接触式三维扫描、袜口处腿截面模型的建立、有限元模拟和曲线拟合,得到了在穿着6款压力袜时“压力/位移”与角度之间的函数关系。

2) 无论受试者穿着何种压力袜,着装时长如何,“压力/位移”与角度之间的函数关系基本保持不变。利用该拟合曲线方程,在已知压力值的情况下,可以得到袜口处腿截面任意角度点、穿着压力袜后任意时长的位移数据。

3) 在压力袜的设计过程中,可以根据压力、位移与角度之间的关系,将袜口设计为松紧不同的区域,以满足人体的着装舒适性需求,该结论为服装压力舒适性的评价和服装结构优化改良提供了参考。此方法同样适用于其他类型的紧身服装。

《丝绸》官网下载

中国知网下载