承压类管道内壁损伤缺陷的低频电磁检测

沈常宇，汪永其，刘 洋，张智超，丁泽宜,，李光海，陆新元，朱周洪

(1.中国计量大学 光学与电子科技学院， 杭州 310018；2.中国特种设备检测研究院, 北京 100029)

承压类管道是重要的气体、液体运输工具。截止目前，我国现有的原油管道长度达到6.5万千米，天然气管道总长度达到10.4万千米。按照国家相关部门发布的文件显示，到2025年底，国内的油气管道总长度将达到约24万千米，形成一个庞大的管道运输网[1]。管道系统的可靠性和有效性常常受到腐蚀、磨蚀、沉积、阻塞等降解因素的影响[2]。为了能够确保管道的安全运行，对管道进行检测是最基本的要求，检测方法包括低频电磁漏磁检测、射线检测、涡流检测、超声检测等[3-7]。汪磊等[8]研究了常规超声使用的单晶探头，发现其声束发射角度单一，不能有效识别出压力容器内表面的点腐蚀缺陷，且只能从波形中识别出较深点腐蚀缺陷的位置，不能确定缺陷类型，容易导致漏检。黄学斌[9]采用红外热像检测技术检测氨制冷压力管道缺陷，根据管道内部温度场的不同来检测内腐蚀缺陷，然而，影响温度场的因素众多，且该检测要求苛刻，实际应用范围不大。唐飞阳亮等[10]在检测锅炉水冷壁管结构件时，为提高点腐蚀型缺陷的检测成功率，采用了数字射线检测方法，但该方法对于腐蚀面积型缺陷的检测灵敏度较低，适用范围有一定的限制。岳庚新[11]采用放置式涡流传感器来检测表面有涂层的管道内部缺陷，发现无法对涂层厚度大于2.5 mm的内部缺陷进行有效检测。可以看出，上述检测方法都有其自身的检测优点，但也有明显的局限性，尤其对于表面存在涂层的管道类设备的缺陷检测还存在不足。因此，研制一种使用方便，穿透性强的高精度检测仪，实现对表面存在涂层的管道类设备缺陷的检测，具有十分重要的意义[12]。

文章基于低频电磁检测基本原理，通过优化传感器结构，实现了对信号的控制、数据放大及滤波处理等功能。研制的承压类管道缺陷低频电磁检测系统，在低磁导率、检测频率为100～200 Hz的情况下，实现了对直径为152 mm，厚度为16 mm，埋深为12.8 mm的304不锈钢材料承压管道缺陷的有效检测。

1 低频电磁检测原理

低频电磁检测原理为使用强磁场磁化待测试件直至试件磁饱和，当试件内部存在缺陷时，试件内部磁场会发生泄漏，对拾取的漏磁场强度及相位进行分析，可以得到缺陷的相关特征，再进一步对拾取数据进行分析，即可实现对缺陷的量化。

低频电磁传感器如图1所示，传感器采用磁芯及缠绕在磁芯上的激励线圈作为励磁装置，缠绕在衔芯上的多匝线圈作为漏磁场拾取装置，高磁导率的拱形金属材料作为磁屏蔽装置。激励线圈在低频率正弦激励激发下产生一个交变的原电磁场，原电磁场穿透待测试件，磁屏蔽层将磁芯下方的原电磁场屏蔽，使得检测线圈可以拾取到更为精准的漏磁场信号，以便后续进行缺陷特征提取。

图1 低频电磁传感器

2 试样制备与试验方法

影响传感器检测灵敏度的因素主要包括磁芯形状、磁芯尺寸(内外半径、厚度等)、检测线圈参数(衔芯尺寸、线圈匝数等),而要实现高灵敏度的低频电磁检测，需要对传感器结构进行分析并进行参数优化。

基于 COMSOL 仿真软件，利用电磁场模块，建立了交流电磁场检测模型(见图2)。通过参数化扫描功能改变参数并控制变量唯一，对上述影响传感器检测灵敏度的因素逐个进行分析，以此为后续的低频电磁检测传感器的设计提供参数指导。

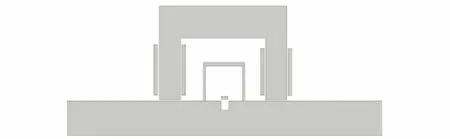
图2 COMSOL交流电磁场检测模型

2.1 磁芯参数仿真及优化

2.1.1 磁芯形状

要想有效地磁化被测试件，磁芯必须能与被测试件形成磁回路，文章采用的磁芯材料为铁基纳米晶体，常用的磁芯形状有U型和C型两种。图3所示为两种磁芯的仿真模型，两磁芯的尺寸相同，绕线匝数为360匝，激励线圈绕线位置为磁芯两极。

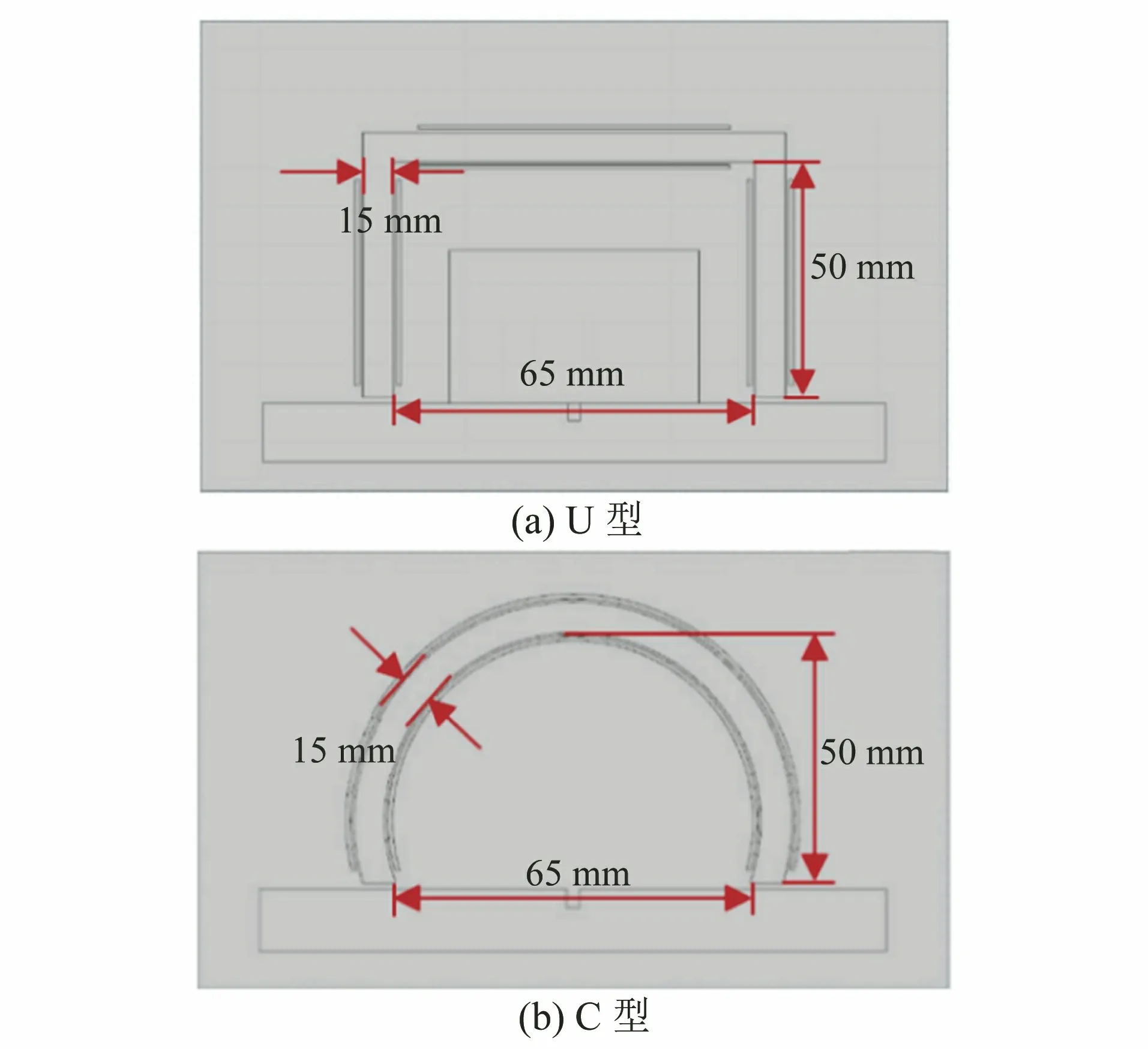
图3 两种磁芯的仿真模型

对两模型施加2 A的激励电流，得到检测信号的仿真结果如图4所示。由图4(a)可知，对于相同的缺陷深度，C型磁芯的检测幅值稍高于U型磁芯的；由图4(b)可知，缺陷深度对两种磁芯的检测灵敏度都有较大影响，但其影响趋势相似，在缺陷深度为2.4～8.4 mm时，C型磁芯传感器的灵敏度稍高于U型磁芯传感器的灵敏度。

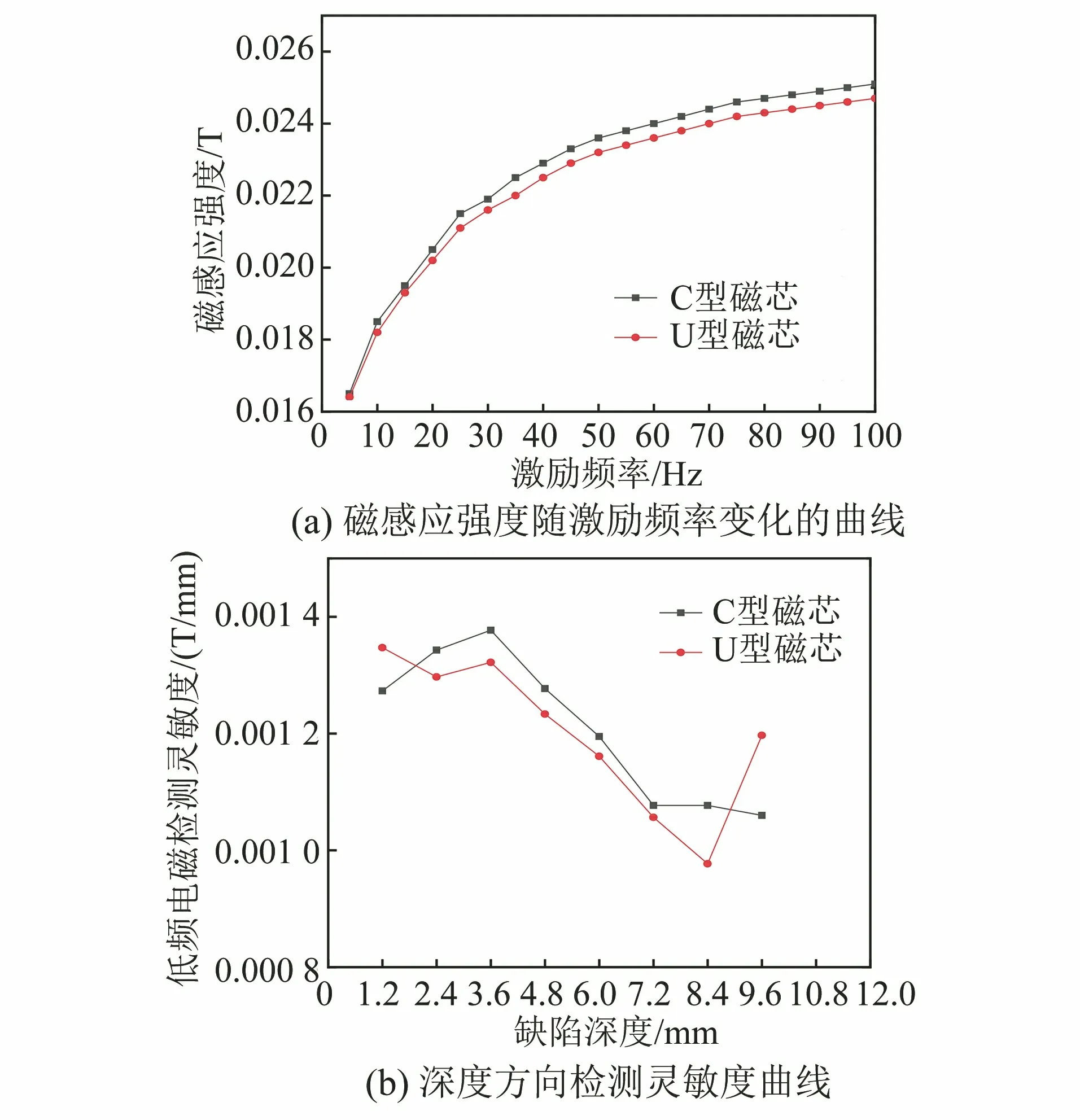
图4 U型和C型磁芯的检测信号仿真结果

2.1.2 磁芯尺寸

进一步研究了C型磁芯尺寸(主要包括磁芯内径弧度θ、磁芯半径R和磁芯厚度W等)对产生磁场的影响，C型磁芯关键尺寸参数如图5所示。

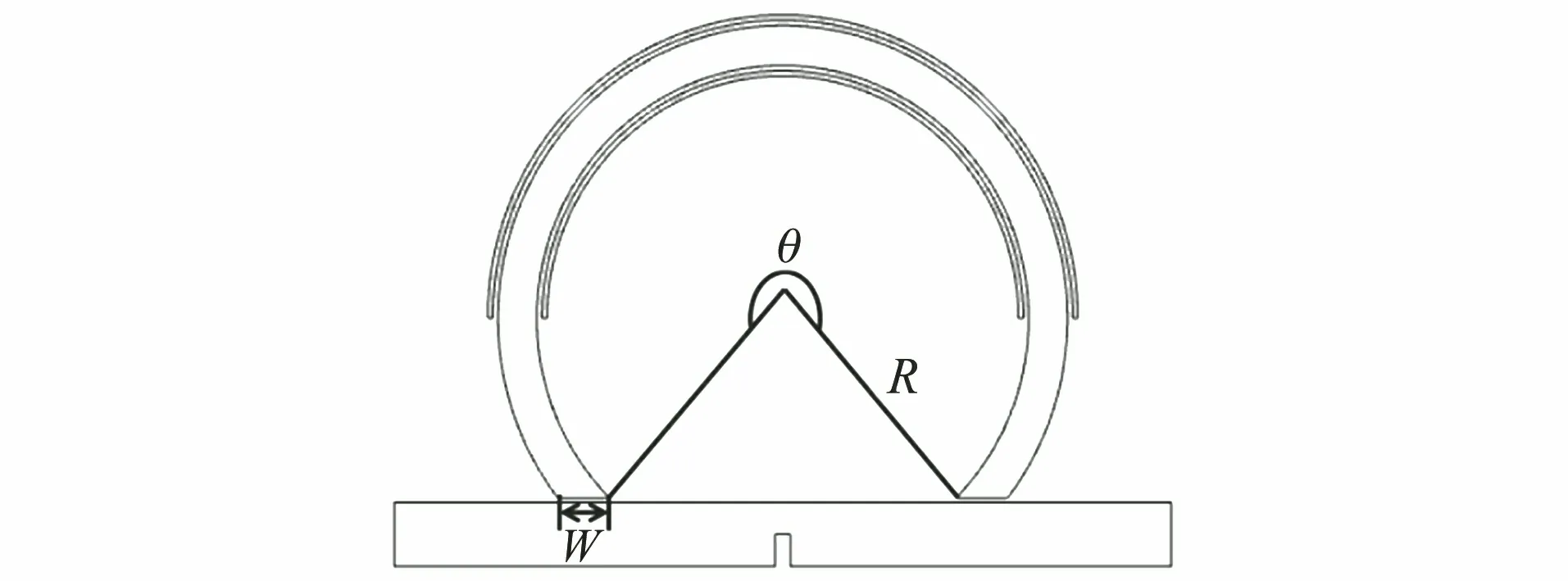
图5 C型磁芯关键尺寸参数示意

控制磁芯半径R为45 mm，磁芯厚度W为15 mm不变，在磁芯内径弧度为180°～260°，变化步长为 20°情况下，提取不同磁芯内径弧度产生的磁感应强度(见图6)。由图6可见，磁芯内径弧度的变化对检测信号的影响较大，在内径弧度为180°时磁感应强度最大。

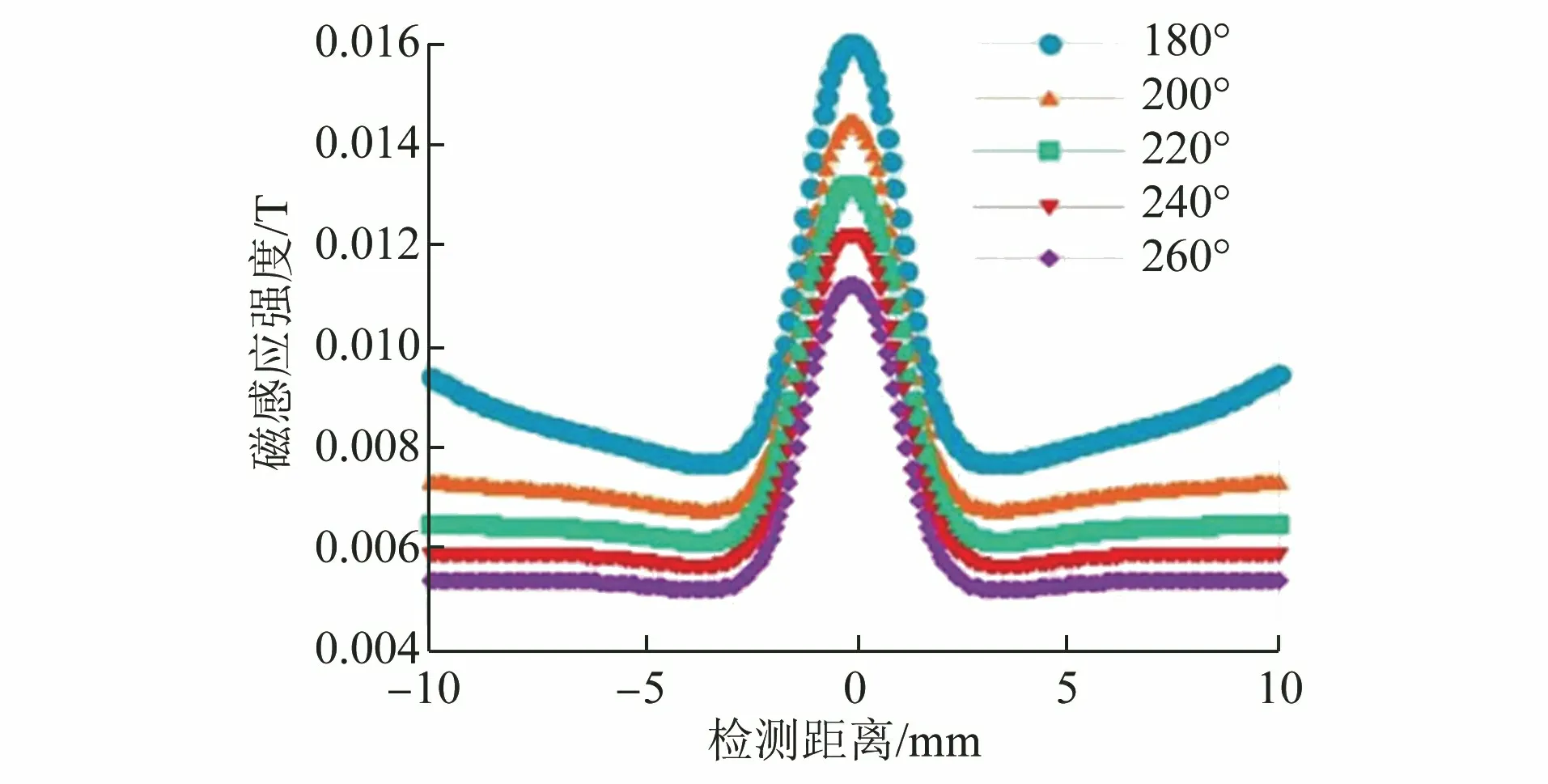
图6 磁感应强度随磁芯内径弧度变化的曲线

提取扫描基准值、缺陷检测峰值和基线最大偏离量3个特征参数，分别获得了如图7(a)所示的缺陷检测峰值随磁芯内径弧度变化的曲线，以及如图7(b)所示的扫描基准值及基准线最大偏离值随磁芯内径弧度变化的曲线。

从图7(a)可以看出，当缺陷深度一定时，磁芯内径弧度越大，缺陷检测峰值越小，即较小的磁芯内径弧度有利于缺陷检测，但从图7(b)可以看到此时扫描基准值和基准线最大偏离值均较大，即此时的扫描结果受背景磁场影响较大，基准线水平较高，且基线平稳度较差，不利于缺陷检测。3个参量之间相互矛盾，无法直接给出最优的磁芯内径弧度。因此，文章将采用遗传算法对磁芯内径弧度进行优化，在算法中找出最优解。

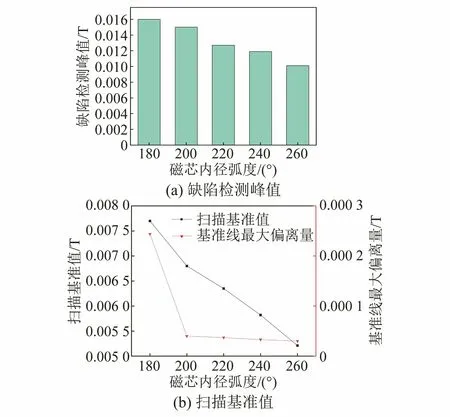
图7 缺陷检测峰值与扫描基准值随磁芯弧度变化的曲线

进一步，研究了磁芯半径对磁化装置磁化性能的影响。设置磁芯内径弧度固定为220°，厚度为15 mm，磁芯半径以10 mm的步长在20～60 mm 间变化，得到了不同磁芯半径下仿真磁感应强度的空间分布(见图8)。由图8可以看出，不同磁芯半径下磁感应强度的空间分布曲线几乎重叠，即磁芯半径对磁感应强度的空间分布无明显影响。因此，在实际制作传感器中，磁芯半径可以根据成本等其他因素设定。

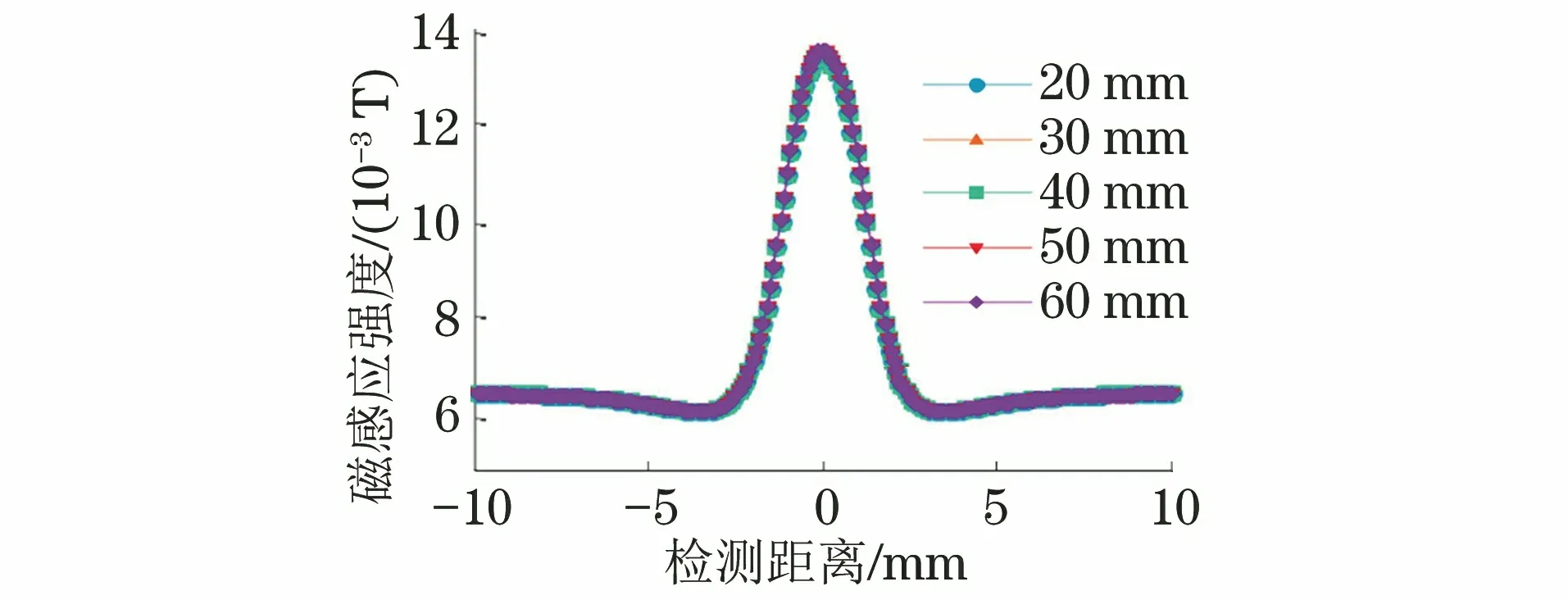
图8 不同磁芯半径下磁感应强度的空间分布曲线

对磁芯厚度对传感器检测性能的影响进行了研究。控制磁芯内径弧度为220°，半径为 45 mm不变，磁芯厚度以2 mm的步长在4～12 mm间变化，获得了其磁感应强度随磁芯厚度变化的分布曲线(见图9)。由图9可以看出，磁芯厚度从4 mm增加到12 mm的过程中，磁感应强度也增大。

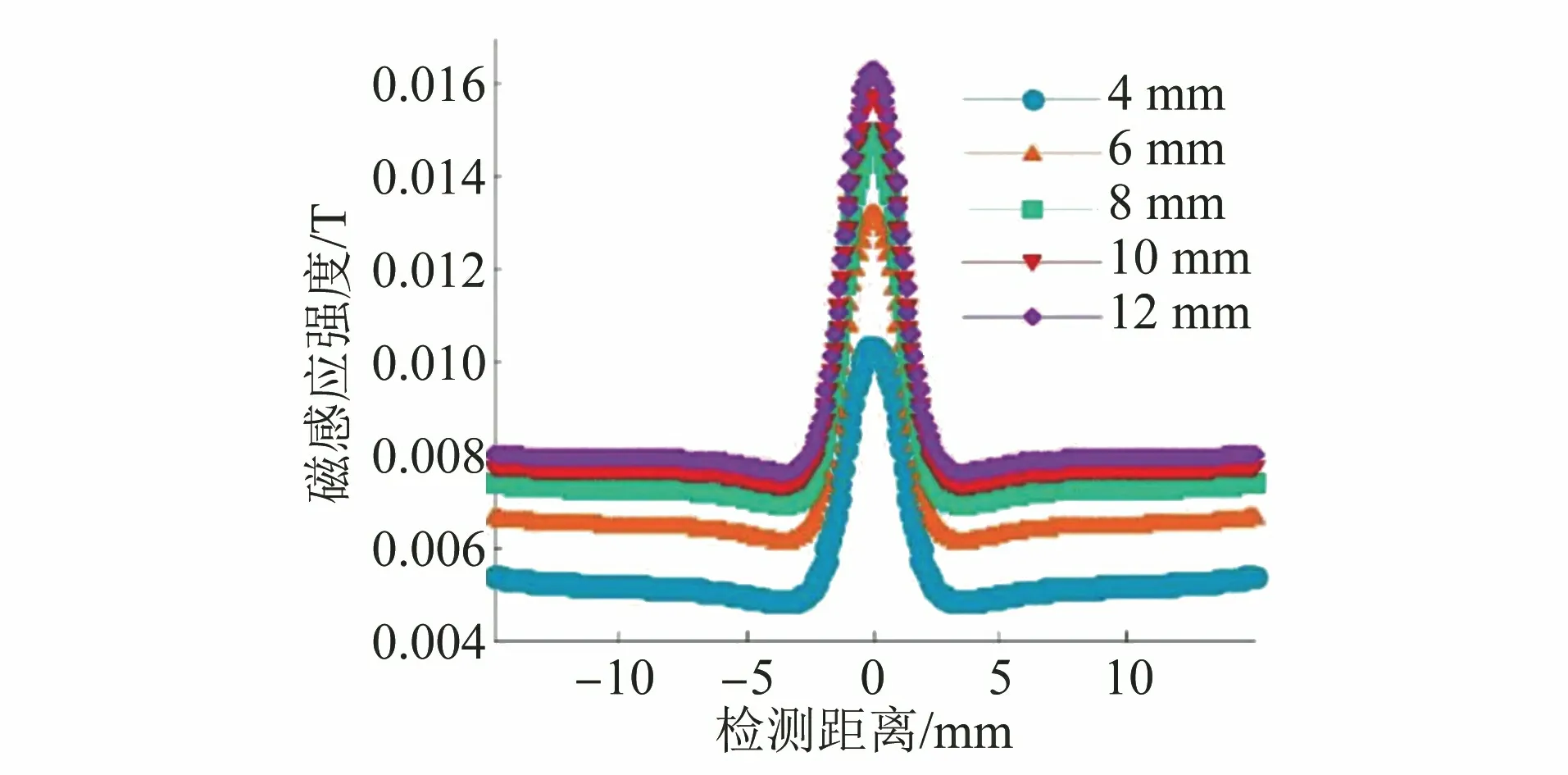
图9 磁感应强度随磁芯厚度变化的分布曲线

缺陷检测峰值与扫描基准值随磁芯厚度变化的曲线如图10所示。从图10可以看出，磁极宽度增加，缺陷检测峰值与无缺陷处的基准值同步上升，二者同时制约着磁芯厚度的选择。文章也采用遗传算法对磁芯厚度进行计算求取最优解。

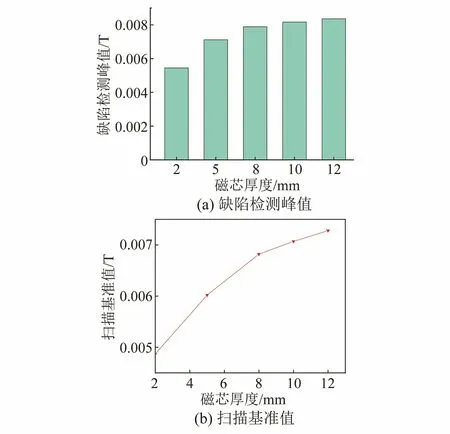
图10 缺陷检测峰值与扫描基准值随磁芯厚度变化的曲线

利用遗传算法优化磁芯内径弧度和磁芯厚度两个参数，遗传算法重实数变量的可行域为[10,130]，二进制编码的精度为 0.096 34。当阈值小于10-3时，优化过程结束。达到该条件的遗传算法优化收敛图如图11所示。由于适应度值达到0.000 019 5时满足收敛条件，根据优化结果，该系统的最佳磁芯内径弧度为220°，磁芯厚度为12 mm。

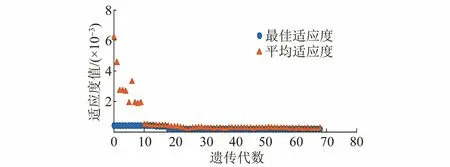
图11 遗传算法优化收敛图

2.2 检测线圈优化

除了激励磁芯的优化设计，检测线圈的优化设计也是传感器优化的重要部分。根据法拉第电磁感应定律，对于一个匝数为N匝的线圈，不考虑线圈间存在间隙，假设每匝穿过的磁通量相同，则线圈的感应电动势E为

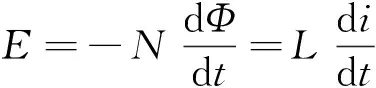
(1)

式中：dΦ/dt为磁通量变化率；L为电感系数，di/dt为电流关于时间的导数。

由式(1)可以看出线圈的感应电动势和电感及匝数呈线性关系，线圈匝数决定了线圈感应电动势的大小，但并不能一味地增加线圈匝数来获得高阻抗，相较于增加线圈匝数，改变线圈电感更易提升检测线圈的阻抗值，电感为

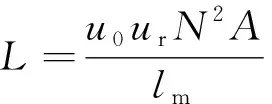
(2)

式中：u0为自由空间磁导率；ur为镍铁合金衔芯的相对磁导率；A为检测衔芯横断面积；lm为对应的磁路长度。

由式(2)可见，影响检测线圈检测灵敏度的主要因素为衔芯尺寸(主要指衔芯直径)及检测线圈匝数。

2.2.1 检测线圈衔芯直径优化

检测衔芯的直径影响接收线圈的电感值，从而影响到传感器的接收能力。在绕制匝数相同的80%Ni+20%Fe镍铁合金条件下，试验采用直径(D)为3.15 mm，3.65 mm，4.15 mm的检测衔芯，对12 mm厚的304不锈钢管道表面孔型缺陷进行检测，检测结果如图12所示。

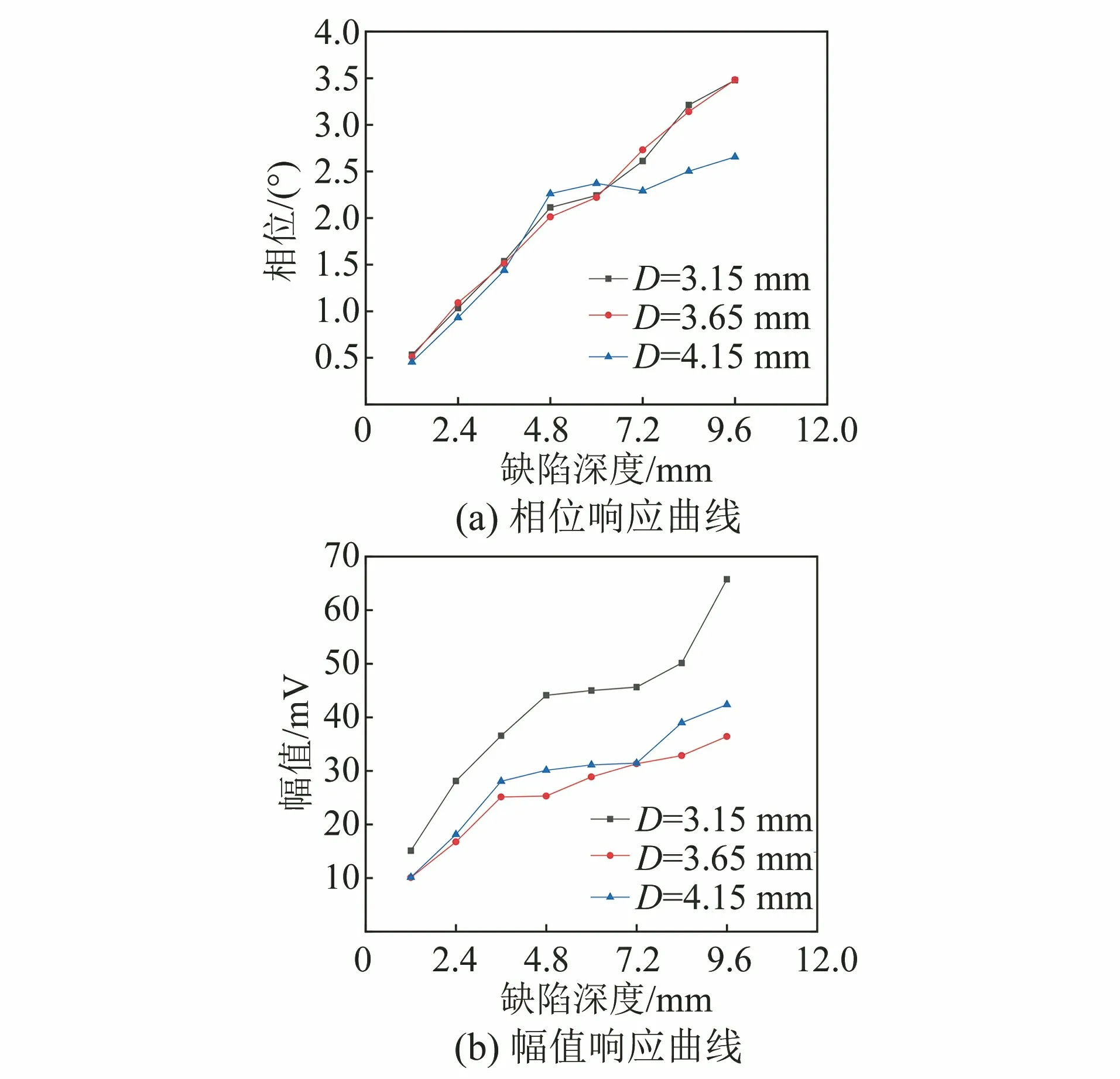
图12 不同直径检测衔芯下缺陷的检测结果

由图12可以看出，检测衔芯直径不变，缺陷处检测幅值与相位信号强度都随着缺陷深度的增大而逐渐增强；在同一缺陷深度下，检测信号强度随检测衔芯直径的增加呈现一定程度的衰减，且当直径为3.15 mm时，检测灵敏度最高。

2.2.2 检测线圈匝数优化

增加检测线圈匝数可以有效提高线圈感应电动势的大小，但同时也易增加检测线圈的阻抗值。为确定最优的检测线圈匝数，选取线径为0.06 mm的漆包线在直径为3.15 mm的检测衔芯上分别绕制8层(480匝)，10层(600匝)，12层(720匝)，再对12 mm厚的304不锈钢管道表面孔型缺陷进行检测，检测结果如图13所示。

由图13可以看出，在相同检测线圈匝数情况下，缺陷处检测幅值与相位信号强度随着缺陷深度的增大而逐渐增强，在同一缺陷深度下，检测信号强度并不随着检测线圈匝数的增加对应增强；在绕满10层(600匝)时检测信号较强，考虑到线圈高度等因素，应选择10层(600匝)的检测线圈。

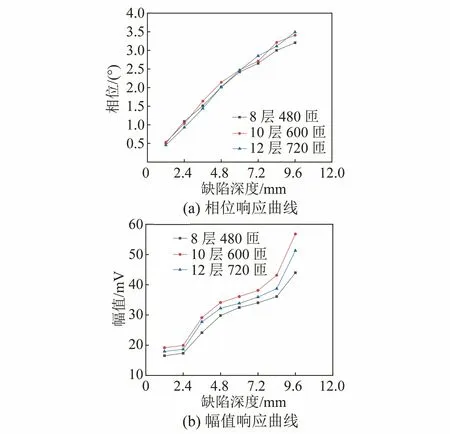
图13 不同检测线圈匝数下缺陷的检测结果

3 电磁检测系统设计及试验

3.1 电磁检测系统设计

研制的承压类管道低频电磁检测系统主要由电磁传感器、信号发生模块、功率放大模块与信号调理模块构成。

3.1.1 电磁传感器设计

电磁传感器由激励模块、检测模块及外壳体组成。前文已经通过COMSOL仿真确定了磁芯及检测线圈的相关参数，具体为采用C型铁基纳米晶体材料作为励磁磁芯，磁芯内径弧度为220°，磁芯厚度为12 mm，激励线圈缠绕在整个励磁磁芯上，磁屏蔽层采用高磁导率的坡莫合金，检测线圈衔芯采用内径为3.15 mm的80%Ni+20%Fe配比镍铁合金，采用600匝的多匝线圈缠绕在衔芯上。

3.1.2 外围模块设计

在低频电磁检测系统中，激励线圈由正弦信号进行激励，信号发生器工作流程如图14所示，具体为：单片机主控电路输出一个高频采样脉冲，分频芯片对高频脉冲信号进行分频，产生低频脉冲；低频脉冲信号经过低通滤波器后产生一个正弦信号，作为激励源；然后在低频信号中插入高频脉冲，对低频信号进行采样。

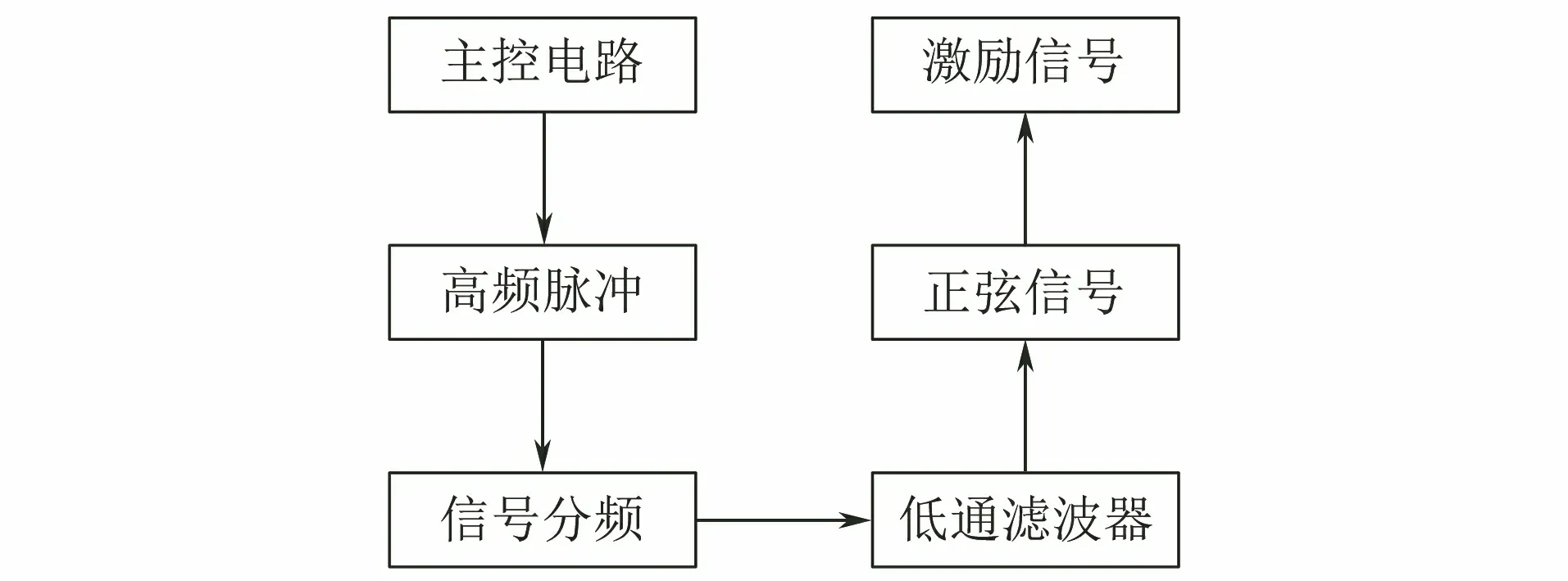
图14 信号发生器工作流程图

功率放大模块采用PA60EU功放芯片和OP07运放芯片来放大单片机主控电路输出的正弦信号，使正弦信号能够作用于激励线圈，从而产生强磁场；信号调理模块主要通过反向低通滤波来放大电路，滤除检测线圈受环境干扰而产生的杂波。

3.2 试验结果与分析

按照承压类管道构件电磁检测国家标准，设计并加工了管道构件检测试块，试块材料为304不锈钢，用于模拟承压类管道构件，管道直径为152 mm，厚度为16 mm。在管道中心位置处加工直径为5 mm，上下表面深度分别为管道厚度的20%，50%，60%，80%，100%的5个缺陷(见图15，T为厚度)。调整电磁传感器的提离高度，开展检测试验，检测现场如图16所示。

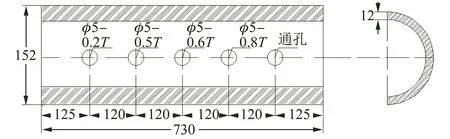
图15 管道腐蚀缺陷设计示意

图16 管道的电磁检测现场

3.2.1 表面缺陷检测试验

检测系统激励频率为100～1 000 Hz，步进为100 Hz，驱动电流为5 A，对厚度为16 mm管道构件表面腐蚀缺陷进行检测，匀速滑动传感器对管道进行扫查，进一步提取检测信号，检测结果如图17所示。

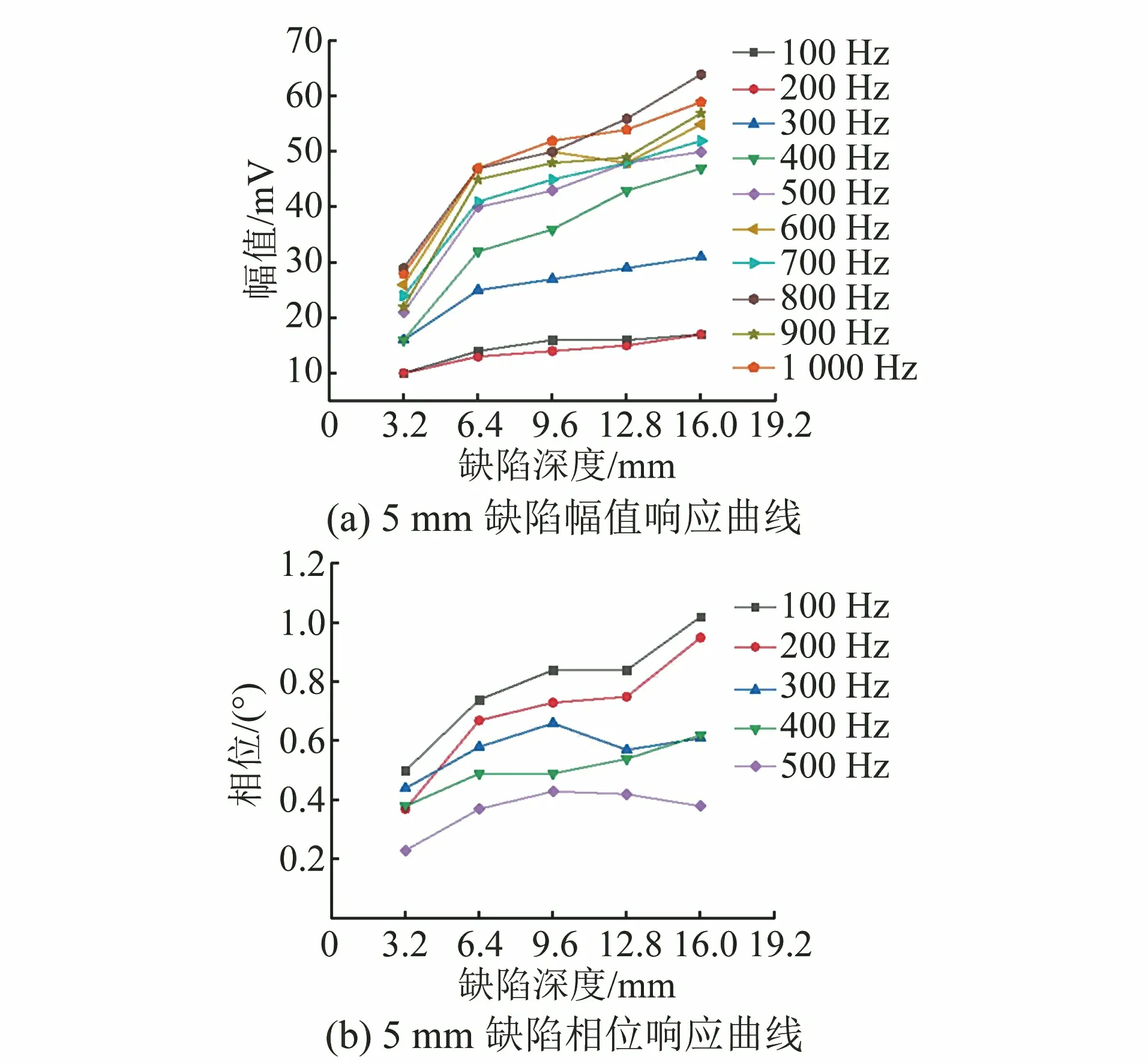
图17 16 mm厚不锈钢表面缺陷的检测结果

由图17可知，检测幅值及相位信号均随着缺陷深度增大整体呈现递增趋势；对于直径为5 mm的缺陷，随频率增大其相位信号减小，激励频率为100～500 Hz均可实现对缺陷的有效检测，且频率约为100 Hz时，幅值响应及缺陷信号响应最强，检测效果最好。

3.2.2 埋深缺陷检测试验

检测系统的激励频率为100～400 Hz，步进为100 Hz，驱动电流为5 A，对16 mm厚的管道构件内部腐蚀缺陷进行检测，匀速滑动传感器对管道进行扫查，提取检测信号，检测结果如图18所示。

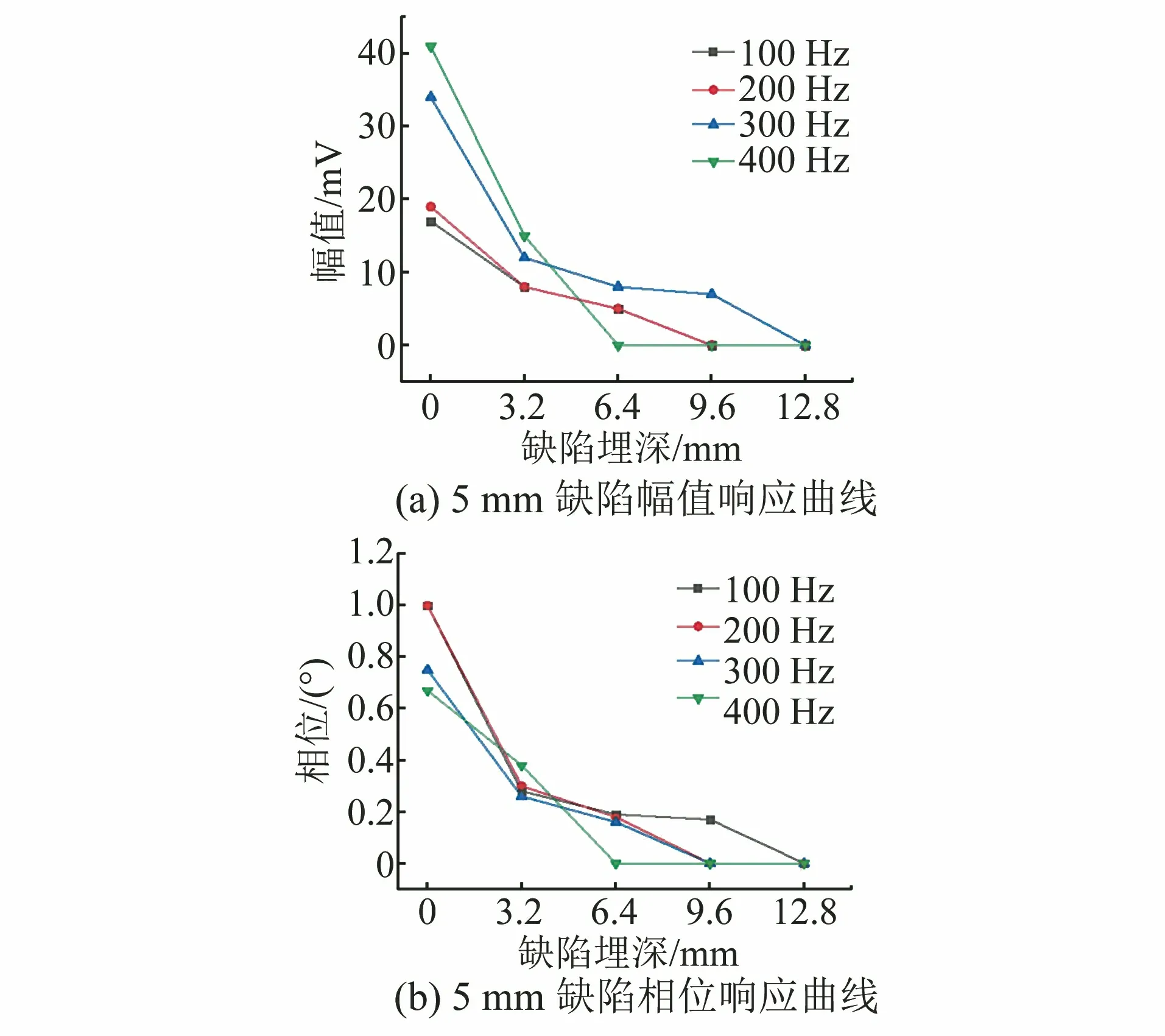
图18 16 mm厚不锈钢埋深缺陷的检测结果

由图18可知，当管道厚度为16 mm时，随着缺陷埋深增加，检测电压幅值与相位均呈下降趋势；采用100～300 Hz输入信号激励时，埋深为9.6 mm以下缺陷的幅值与相位均有明显变化，说明该系统可以实现对埋深为9.6 mm以下缺陷的检出，但对于埋深为12.8 mm左右的缺陷，仅在频率为100～200 Hz时，采集到的幅值与相位差明显，可以实现缺陷检出。

3.3 检测结果

采用研制的承压类管道低频电磁检测系统，对不同参数的缺陷开展了试验研究，分析了激励频率对低频电磁检测信号的影响，获得了如下结果。

(1) 对304不锈钢管道而言，增大激励频率，检测信号幅值整体上呈现递增趋势，检测相位信号呈现先递减再递增趋势，激励频率为500～600 Hz时，检测信号无法有效表征缺陷，最佳检测频率为100～200 Hz。

(2) 分析了裂纹缺陷的检测信息，发现缺陷处检测幅值及相位信号强度随着缺陷深度的增加而增强；随着缺陷埋深的增大，检测信号强度严重衰减，不利于缺陷的有效表征。

(3) 研制的检测系统对304不锈钢的穿透深度可达16 mm，对5 mm宽圆形缺陷的有效检测深度达管道厚度的60%，系统功能完整，性能良好。

4 结语

设计研制了承压类管道低频电磁检测系统，利用仿真对比试验完善了低频电磁传感器的内部结构。试验表明，该系统对于管道的最佳检测频率为100～200 Hz，可实现对直径为152 mm，厚度为16 mm，埋深为12.8 mm的304不锈钢管道内部缺陷的有效检测。该系统灵敏度高、穿透性强，体积小，在承压管道内部损伤无损检测领域具有较好的应用前景。