基于矩阵半张量积的模糊逻辑研究进展

孙长乐，李海涛

(山东师范大学 数学与统计学院，山东 济南 250358)

0 引言

模糊逻辑利用部分专家知识或有限的实验数据来处理系统的复杂性、非线性与不确定性，是复杂系统建模与控制的革命性方法[1,2]。自Zadeh于1988年提出模糊逻辑以来[3,4]，经过三十多年的研究发展，模糊逻辑已经引起了许多学科的关注并已成功应用于众多领域：控制工程[5-7]、计算机网络[8-11]、故障检测与诊断[12-16]、模式识别[17-20]等。

模糊推理是模糊逻辑系统最为核心的部分，一般可分为两类：Mamdani规则推理[21]、T-S模糊推理[22]。模糊推理可分为前提与结论两部分，Mamdani规则推理与T-S模糊推理前提部分相同，但是Mamdani规则推理在结论部分输出为模糊子集，而T-S模糊推理在结论部分输出为多项式函数。Mamdani规则推理具有更好的解释能力，而T-S模糊推理一般与优化算法相结合具有更好的逼近能力。模糊推理通过模糊规则将人类推理与模糊信息联系起来去处理复杂系统，并进行多方面的扩展研究。例如，遗传模糊系统[23-25]将遗传算法与模糊系统相结合，对模糊规则进行设计、优化，并使其具有一定的学习能力。模糊神经网络[26-29]将神经网络的学习能力与模糊系统的解释能力相结合可更有效的处理复杂系统。分层模糊系统[30-33]利用多个低维模糊子系统构建大规模模糊系统，减少系统模糊规则数量，简化模糊推理过程。

模糊推理过程本质上是模糊逻辑处理过程，现有处理模糊逻辑系统的数学方法少之又少，模糊逻辑系统研究过程中迫切需要一个恰当的数学工具以求突破。近年来，程代展教授及其团队提出矩阵半张量积理论，突破了普通矩阵乘积维数的限制，还能保持普通矩阵乘积的性质[34-36]。矩阵半张量积将模糊推理过程转化为代数形式，从而有效简化了模糊推理过程。特别是对于具有多重耦合模糊关系的多输入多输出模糊系统，当多重耦合模糊关系不可按控制进行分解时，多个模糊控制器必须同时设计，其它模糊逻辑理论中逐个设计模糊控制器的方法就不再适用，而基于矩阵半张量积框架的模糊控制器设计方法为解决此类问题提供了便捷的研究框架。基于矩阵半张量积的模糊逻辑的理论核心为模糊关系矩阵，在其它模糊逻辑理论中，当输入变量的个数N>2时，模糊关系矩阵会受到维数的限制，很难进行准确、简洁的表示。但利用矩阵半张量积理论，模糊关系矩阵突破了维数的限制，进而将模糊推理过程转变为代数形式，借助相应的代数理论知识，可以更加简便的研究模糊逻辑理论。基于矩阵半张量积框架的模糊系统研究取得了重大的理论突破且已成功应用于实际系统控制，包括原料质量控制系统[37]、电力工业[38，39]、废弃物处理[40]、空调系统设计[41-48]等。

随着矩阵半张量积理论的提出，逻辑系统研究取得了重大突破并成功应用于众多方向，包括动态博弈[48-51]，动态-静态布尔网络[52-56]与网络化系统的建模及安全性分析[57-60]等。程代展教授在矩阵半张量积框架上对混合值逻辑定义、运算以及应用给出了一个较为系统的综述[61]。然而，对基于矩阵半张量积框架下的模糊系统研究进展鲜有较为系统的总结，本文旨在对基于半张量积理论的模糊系统发展研究进行综合概述，并给出基于矩阵半张量积理论的模糊系统的研究前景。

1 数学基础

1.1 符号简介

(1)Mm×n为m×n阶实矩阵构成的集合。

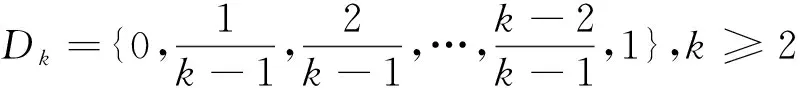
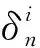
(6) 给定α，β∈Dk，α与β的布尔乘α×Bβ，定义为α×Bβ=(α∧β)，∧为“合取”逻辑算子。

1.2 矩阵半张量积

矩阵A、B做普通矩阵乘积时，A的列数必须等于B的行数。矩阵半张量积是普通矩阵乘积的推广，突破了矩阵A、B做普通矩阵乘积时维数的限制，同时还保持了普通矩阵乘积的性质。

矩阵半张量积可以将逻辑算子转化为矩阵形式，是逻辑演算代数化的一个重要方法，并已经得到了广泛的应用[62-65]。

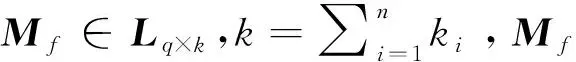
下面通过一个例子来说明混合值逻辑映射的代数化，以便读者理解。

给定逻辑变量x1∈Δ2，x2∈Δ2，x3∈Δ2，逻辑函数f(x1,x2,x3)=x1∧x2∨x3，则有形式

式中合取逻辑算子的矩阵表示形式Mc=δ2[1 2 2 2]，析取逻辑算子的矩阵表示形式Md=δ2[1 1 1 2]，结构矩阵Mf=δ2[1 1 1 2 1 2 1 2]。

2 模糊控制系统研究进展

模糊推理是模糊控制系统中最重要也是最复杂的一部分，现有对模糊推理进行分析研究的数学方法较少。随着程代展教授提出矩阵半张量积理论，并与其团队取得了一些基本研究成果，为模糊集描述与一般模糊关系描述提供了一种新方法。利用矩阵半张量积方法可以将模糊推理过程转化为代数形式，使得模糊推理过程研究取得了突破性进展。

2.1 历史回顾

模糊控制系统一般分为模糊化、知识库、模糊推理、解模糊化四部分，其中以基于模糊规则求解模糊控制量的模糊推理为核心部分[66，67]。模糊推理在处理系统不确定性、随机性与复杂性方面有着天然的优势。模糊推理一般可分为Mamdani规则推理与T-S模糊推理，模糊规则表达式为“IFXisATHENYisB”，其中，Mamdani规则推理类型中“B”为模糊子集[68，69]，T-S模糊推理中“B”为与变量X相关的多项式[70-74]。

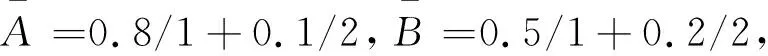
(1) 求取矩阵D，其中dxy=μA(x1)∧μB(x2)

(2) 求取模糊关系矩阵MR

除上述通过模糊关系矩阵进行模糊推理以外，还可以通过隶属度函数图像进行模糊推理。模糊系统中输入变量个数r≤2时，模糊推理过程通过模糊关系矩阵可以转化为代数形式，简化推理过程，降低推理过程的复杂度。当r≥3时，从步骤(1)、(2)可知，模糊关系矩阵变为r维矩阵，无法应用于模糊推理过程，模糊推理过程计算复杂度剧增。但模糊控制系统具有设计简单，实现性较强，控制效果明显等优点，在各方面得到了广泛的应用，因此多输入变量模糊系统的模糊关系矩阵研究是一个比较重要且有意义的课题。

2.2 模糊控制系统最新研究进展

基于矩阵半张量积方法，文献[75-77]将模糊推理过程转化为模糊关系矩阵进行代数运算，不再受系统输入变量个数的限制，即模糊关系矩阵不受维数的限制，模糊推理研究取得了突破性进展。

基于矩阵半张量积理论，模糊关系矩阵不再受维数的限制。为了文章紧密性，通过两输入单输出模糊系统对模糊关系矩阵进行介绍。系统输入变量X={x1,…,xm}、Y={y1,…,yn}，输出变量Z={z1,…,zr}，隶属度值{μR(xi,yj,zk)|i=1,…,m;j=1,…,n;k=1,…,r}按Id(k;r)×Id(i,j;m,n)顺序进行排列，进而构建系统的模糊关系矩阵

如图1模糊控制系统结构框图所示，基于矩阵半张量积方法，模糊关系矩阵替代模糊规则，将模糊推理过程转变为代数运算过程，简化其计算复杂度，降低了模糊控制器设计的复杂性。

图1 模糊控制系统结构框图

为便于读者理解，下面用一个例子来说明基于矩阵半张量积理论的模糊推理过程。

给定两输入单输出的模糊控制系统，系统输入变量A、B均有7个模糊子集{NB,NM,NS,ZO,PS,PM,PB}，输出变量U有13个模糊子集{NVB,NB,NMB,NMS,NS,NVS,ZO,PVS,PS,PMS,PMB,PB,PVB}。给定模糊输入VA=[0 0 0.75 0.25 0 0 0]T，VB=[0 0 0 0 0.25 0.75 0]T，模糊规则如表1所示，求模糊输出VU。

表1 系统模糊规则表

通过模糊规则表可知此系统的模糊关系矩阵

基于模糊规则表可求得模糊关系矩阵，然而在实际应用过程中，有些模糊控制系统无法直接给出模糊控制规则表，只有相应的系统测量数据，此时模糊关系矩阵求解就会相对困难。为此，文献[78]在隶属度函数中参数不确定时基于最小二乘法等优化算法利用测量数据对参数进行逼近，进而间接求取模糊关系矩阵；当系统变量模糊集对应的隶属度参数准确时，基于测量数据使用直接法对模糊关系矩阵进行求解。例如对三输入单输出模糊控制系统，给定P组测量数据，模糊关系矩阵求解过程如：

(1) 指定测量数据中任意一组输入输出数据(x1i,x2i,x3i,yi)，对其进行模糊化，求解其向量表示形式Vx1(x1i)Vx2(x2i)Vx3(x3i)Vy(yi)。

文献[79]提出了基于模糊关系矩阵的多输入多输出模糊系统的通用逼近方法，从理论上证明了该框架下的模糊系统能够以所需的精度逼近非线性函数，并通过仿真验证了其有效性。模糊系统中控制规则完备时，模糊关系矩阵是唯一确定的，模糊规则非完备时，模糊关系矩阵有多个。文献[80]针对模糊随机变量，将概率转移矩阵与模糊关系矩阵相结合，提出了随机模糊控制器的设计方法，当模糊规则完备时，随机模糊控制器是唯一确定的。

3 分层模糊控制系统研究进展

3.1 历史回顾

模糊系统中控制规则会随着系统输入变量的增加呈现出指数增长的趋势，即给定的模糊系统有m个输入变量，每个变量有n个模糊子集，那么模糊规则有nm条，输入变量增加p个，模糊规则数量变为nm+p条，这种现象称为“维数灾难”。模糊规则数量增多会增加模糊控制器设计的难度与模糊推理的复杂度。为处理模糊系统“维数灾难”问题，文献[81]提出了分层模糊系统的思想，即整个模糊系统由多个低维模糊子系统构成，使得模糊规则的数量会随着输入变量个数的增加呈现线增加，有效减少了大规模模糊系统的模糊规则数量[82]。分层模糊控制系统已广泛的应用于航空航天[83，84]，机器人控制[85，86]，社会管理[87]等领域[88-91]。

分层模糊控制系统设计过程中，中间层涉及的模糊规则结构几乎没有任何物理意义，其规则解释性较弱，难以设计[92]。文献[93]提出一种新的映射规则库方案，基于原系统模糊规则获取分层系统的模糊规则，增强了中间层系统设计的可解释性。分层模糊控制子系统之间经过解模糊化、模糊化过程，控制变量的精度会受到影响。针对此问题，文献[94]提出一种基于转移矩阵快速推理获取分层模糊系统矩阵表达形式的方法，构造辅助矩阵，有效避免了中间层人工参与过程，使得中间层系统设计更加透明。

3.2 分层模糊系统最新研究进展

基于矩阵半张量积方法，分层模糊系统研究取得了较大进展。文献[95]提出基于矩阵半张量积方法的分层模糊系统实现方法，构建了分层模糊系统的矩阵半张量积代数框架，基于混合值逻辑函数的半张量积分解方法，降低了中间层设计的复杂度，使得中间层系统设计更加透明。

分层模糊系统可分为串联、并联与混合分层模糊系统，其中混合分层模糊系统为串联与并联分层模糊系统的组合，因此综合运用串联、并联层次模糊系统实现方法即可构建混合分层模糊系统。

串联分层模糊系统的代数表达形式如

(1)

并联分层模糊系统的代数表达形式如

(2)

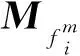
基于混合值逻辑函数的矩阵半张量积分解方法，整个模糊系统的结构矩阵可以分解为形如串联、并联分层模糊系统中子系统的结构矩阵，进而获取分层模糊系统中子系统的结构矩阵。基于矩阵半张量积分解的方法，将模糊推理过程转化为代数形式，使得设计过程更加透明、简洁，其次，在中间层子系统设计过程中不需要人工参与也不需要构建辅助矩阵，并降低了分层模糊控制系统的计算复杂度。

4 模糊关系方程与模糊关系不等式研究进展

4.1 历史回顾

模糊关系方程与模糊关系不等式方程求解问题是模糊集与模糊系统领域最重要的问题之一。由于其重要性与研究难度，该问题一直是富有挑战性的研究课题[96，97]。

模糊关系方程求解问题可诠释为给定模糊集A∈F(U×W)、B∈F(U×V)，寻找一个X∈F(W×V)满足

A∘X=B。

(3)

文献[98]提出了一种模糊关系系统的识别算法，该算法对系统模糊数据或非模糊数据进行聚类，构建基本模糊集，并根据相应的性能指标对模糊关系进行计算。文献[99]提出基于规则的方法，使用符号矩阵与辅助矩阵，求解最广泛的解决集。文献[100]通过排除规则事先排除冗余解，并通过构建准则矩阵和辅助矩阵给出了求解模糊关系的算法，通过简单的逻辑运算即可求得独立的解集。

模糊关系不等式方程表示为

s≤A∘x≤t，

(4)

式中s=[s1,s2,s3,…,sm]T，A=(aij)∈[0,1]m×n，x=[x1,x2,x3,…,xn]T，t=[t1,t2,t3,…,tm]T。

文献[101]定义了模糊关系不等式路径，简化了模糊关系不等式求解过程，并给出受限于多个模糊关系不等式的目标函数优化算法，缩小优化搜索范围。文献[102]对这一算法进行简化，并给出了模糊关系不等式路径与最小解之间的关系，提出了具有模糊关系不等式约束的优化问题的新解法。文献[103]讨论了模糊关系不等式最小解的唯一性，通过定义关键集、关键系统给出了求解模糊关系不等式的算法。

4.2 模糊关系方程最新研究进展

给定逻辑方程

(5)

(1) 根据逻辑方程构造有序集合Ξ={0, 0.32, 0.68, 1}

(3) 基于矩阵半张量方法，将逻辑方程转化为代数形式

(6)

式(4)可进一步写为

由向量形式转化为模糊值

4.3 模糊关系不等式最新研究进展

基于矩阵半张量积理论，文献[108，109]定义相关参数集，并证明了模糊关系不等式解集最小解的唯一性，提出了求解模糊关系不等式全解的算法。下面通过一个例子来介绍相关算法。

(7)

(1) 根据逻辑方程构造有序集合Ξ={0, 0.1 0.2 0.3, 0.5, 0.7 0.9 1}。

(2) 将集合Ξ中的元素转化为向量形式

(4) 求得解集Γ=Γ1∩Γ2，并求出解集中最大解对应的模糊值为[0.5 1]T，最小解对应的模糊值分别为[0.2 0]T与[0.0.2]T，模糊关系不等式的全部解可表示为

文献[110]将这一结果进行扩展，将更为广泛的五种模糊关系不等式转化为式(2)的形式，利用参数集进行求解运算，并给出了相应的求解算法。文献[111]对基于布尔半张量积复合算子的模糊关系不等式进行了研究，通过构造参数集的方法，求得其模糊关系不等式的所有解。

5 基于矩阵半张量积方法的模糊控制系统应用研究进展

利用矩阵半张量积方法，构建模糊关系矩阵替代模糊规则进行模糊推理过程，大大简化了模糊推理过程，为模糊逻辑分析与推理提供了新方法，并成功应用于实际控制系统。

通过文献[112]中混合动力电动汽车能量管理与控制系统介绍基于矩阵半张量积方法的模糊控制系统实际应用过程。车辆行驶期间，电池电量充足时，车辆电动机主要由电池供电；电池电量不足时，发动机工作，一方面给电池充电，另一方面为电动机工作提供能量；当发动机所提供的能量不足以使电动机正常工作时，电池会为电动机提供能量。

混合动力电动汽车能量模糊控制系统以电池储能状态(SOC)、驾驶员命令指令(Pdriver)与电机转速(ωEM)为输入变量，发动机功率(Pgen)与比例因子(scalefacctor)为输出变量。电池储能状态有四个模糊子集{toolow,low,normal,toohigh}；驾驶员功率命令有两个模糊子集{normal,high}；电机转速有三个模糊子集{low,optimal,high}。输入变量的隶属度函数如图2所示。

注：(a) 电机转速的隶属度函数；(b) 发动机功率的隶属度函数；(c) 比例因子的隶属度函数。图2 输入变量的隶属度函数

系统模糊规则表示如

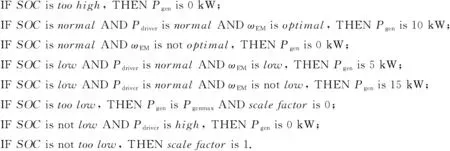
系统模糊规则可表示为

基于模糊规则可得此系统的模糊关系矩阵为

混合动力电动汽车能量模糊控制系统的输出表示如y1=MR1x1x2x3，y2=MR2x1x2x3。

基于文献[112]所提出的最小入度控制算法，检查输入变量中是否存在冗余变量。首先对x1进行检查，将模糊关系矩阵MR1等分为4部分

MR1=δ5[ 5 5 5 5 5 5 2 4 4 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1]。

可见MR1均匀分割为4个不相同模块，则说明x1不是冗余变量。其次分别对x2、x3进行检查

得知x2、x3均不是y1的冗余变量。类似的，对x1、x2、x3是不是y2的冗余变量进行检查，得知x2、x3为y2的冗余变量，矩阵MR2可简化为MR2=δ2[2 1 1 1]。

假设输入变量x1为0.8，x2为45 kW，x3为450 rad/s，其向量形式表示如

模糊输出变量y1、y2可表示为

采用重心法进行解模糊化，系统实际输出变量y1为3.3，y2为1。混合动力电动汽车能量模糊控制系统采用矩阵半张量积理论，利用模糊关系矩阵替代了模糊规则，简化了模糊推理过程，加快了系统的响应。

6 结论与展望

近年来，基于矩阵半张量积理论的模糊逻辑系统研究已经得到了国内外众多学者的关注，其理论研究成果在机器人控制、混合动力车辆控制、电力系统控制等实际系统应用方面得到了验证。基于半张量积的模糊逻辑理论与其它模糊逻辑理论的对比分析如：(1) 对于多输入单输出模糊系统，在其它模糊逻辑理论中，当输入变量的个数N>2时，由于维数的限制，模糊关系矩阵很难准确、简洁的表示出来，进而导致模糊推理过程的计算复杂度增加，且随着系统输入变量的增多，模糊推理过程的计算复杂度剧增；而利用矩阵半张量积理论，模糊关系矩阵的维数突破了维数的限制，进而可以大幅度降低模糊推理过程的计算复杂度，缓解实际应用过程中内存使用问题与实时性能问题。(2) 对于具有多重耦合模糊关系的多输入多输出模糊系统，当多重耦合模糊关系不可按控制进行分解时，多个模糊控制器必须同时设计，其它模糊逻辑理论中逐个设计模糊控制器的方法便不再适用，而基于矩阵半张量积框架的模糊控制器设计方法便可解决此类情况。

模糊系统的主要缺点是不能适应变化的情况，为此利用数据驱动的模糊推理系统[113]或将模糊系统与神经网络、遗传算法相结合都能很好的处理这种情况[114]。另一方面，建立模糊规则的知识是不确定性的，这种不确定性反映在不确定的前件或结论的隶属度部分，I型模糊系统是不能直接处理这种不确定性的，为此，II型模糊系统的概念被提出，通过模糊化隶属度函数来处理这种不确定性[115]。对于基于矩阵半张量积框架的模糊逻辑理论方面，文献[78]利用系统数据构建模糊关系矩阵模型来改善模糊系统适应性问题，但鲜有文献研究II型模糊系统或者模糊系统与神经网络、遗传算法的结合问题。现有文献大部分致力于完善基于半张量积的模糊逻辑理论底部框架，仍需大量学者对其进行研究与探讨。

针对矩阵半张量积框架下模糊逻辑系统分析与控制这一基本课题，虽然取得了一系列优秀的研究成果，但仍有部分问题尚需解决：(1) 模糊推理过程一般可分为Mamdani规则推理与T-S模糊推理。现有研究主要集中在如何利用矩阵半张量积理论构建模糊关系矩阵，将Mamdani规则推理过程转化为代数过程来简化推理过程，对于T-S规则推理过程研究较少。(2) 利用矩阵半张量积理论所构建的多输入多输出模糊系统的模糊关系矩阵维数较大，如何进一步缩小模糊关系矩阵的维数，是一个比较有意义的课题。(3) 矩阵半张量积理论是模糊逻辑表达式转化为代数表达式过程中的重要数学方法，进一步完善矩阵半张量积理论，进而克服模糊系统“维数灾难”现象，是一个较为重要且有意义的课题。