对“同心协力”最佳击球策略问题的分析与探讨
李帅君,张亚鹏,陈金光
(1.赤峰学院 数学与计算机科学学院,内蒙古 赤峰 024000;2.郑州工商学院 工学院,河南 郑州 451400)
1 引言
1.1 研究背景
本文问题背景来源于2019年全国大学生数学建模竞赛B题[1]。
“同心鼓”是团队成员之间练习团队合作技能的拓展项目。该拓展项目是由一面牛皮双面鼓构成,由多根绳子固定于鼓身,绳子的固定点均匀分布于鼓身一周,并且每根绳子的长度相同。每位团队成员拉一根绳子使得鼓面处于水平状态。在项目开始时,球由鼓面中心正上方竖直落下,团队成员相互协作将球颠起,维持其在鼓面上的弹动。颠球期间,队员的手只能抓在绳子的尾部,不允许触碰鼓或绳子的其他部分。项目中使用排球的重量为270g。鼓的质量为3.6kg,鼓身的高度为22cm,鼓面的直径为40cm。其中队员人数大于或等于8人,相邻队员之间的最短距离应大于或等于60cm。项目由初始状态开始时,球由鼓面中心正上方40cm处竖直落下,球颠起后距离鼓面的高度应大于或等于40cm,如果小于40cm,则此次项目结束[2]。该项目的研究目标是团队成员相互合作保持尽可能多的连续颠球次数。
经过阅读相关资料后,目前关于对“同心协力”击球策略问题的研究较少,其中郑学谦在参考文献[1]中通过使用VC++进行编程求解,运用相关参数关系表达式构建鼓的运动模型,给出了鼓面在弹力一致且均匀的情况下,队员在发力出现误差时的最优调整策略。毛紫阳在参考文献[2]中通过微分方程和惯量矩阵建立了鼓面倾斜模型,讨论了在最小的力或最少的做功条件下的最优策略,给出了队员用力出现误差时对鼓的影响与鼓面倾斜时精确的调整方案。本文通过建立排球和鼓的物理模型,对其运动状态进行受力分析和力的合成,建立排球与鼓之间的功能关系,使用动量定理和冲量表达式,分析排球与鼓在发生碰撞前后的运动情况并对得到的数据,最终给出在不同状态下使排球颠球次数最多的最佳击球策略。
1.2 问题要求
(1)在理想状态下,每位团队成员都可以准确控制其自身的用力方向、时机和力度,尝试讨论团队成员之间的最佳协作策略,并得出此类策略下保持颠球的高度[2]。
(2)在实际情形中,每位团队成员的发力时机和力度是有缺陷的,不可能做到完全的精确控制,存在一定误差,最终可能会导致鼓面出现倾斜的状态。假设队员人数为8人,绳子的长度为1.7m,鼓面初始时刻的状态是水平静止的,初始位置的高度比绳子水平时的高度下降了11cm,表1中给出了每位团队成员的不同发力时机和力度,计算0.1s时鼓面的倾斜角度[2]。

表1 发力时机(单位:s)和用力大小(单位:N)取值
(3)当鼓面发生倾斜时,球弹起的方向不再竖直,于是需要团队成员调整各自的拉绳方式。假设人数为10人,绳长为2m,球的弹起高度为60cm,相对于竖直方向产生1°的倾斜角,并且倾斜的方向在水平面上的投影指向某两位团队成员之间,与这两位团队成员之间所产生的夹角比例为1:2。为了将球改变为竖直方向的弹跳状态,给出在能够精确控制的条件下每位团队成员的发力时机和力度[2]。
2 模型假设与理论基础
根据问题所提出的在不同运动环境下分析鼓与球在指定时间内的状态,做出如下假设:
(1)假设1:人静止不动。
(2)假设2:球不受空气阻力,与鼓接触面的摩擦力和弹力。
(3)假设3:问题(2)中的两人为质点。
基于基础数学、牛顿第二定律、受力分析、力的合成与分解、功能关系、动量定理和冲量表达式等基本定理,对排球和牛皮双面鼓的物理运动模型进行分析和计算,将最终得出的结果加以讨论,解决上述最佳协作策略问题,得出最优击球策略。文中使用的部分公式符号说明如表2所示:
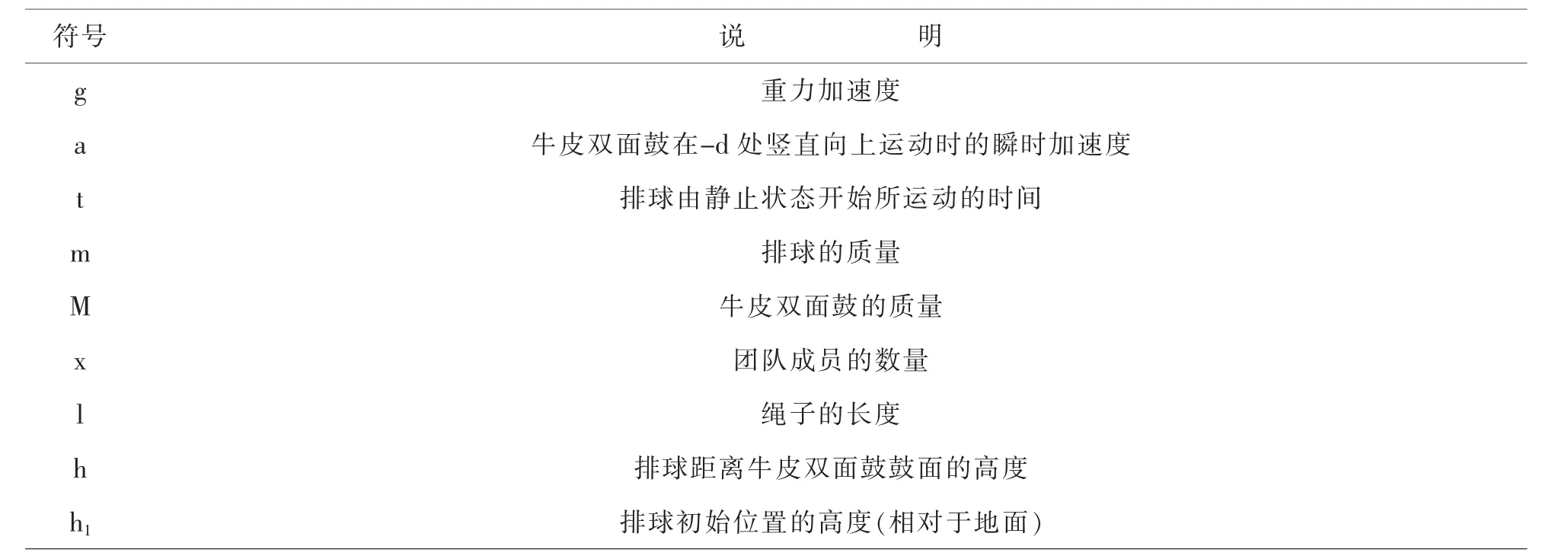
表2 符号说明

符号 说 明h2 排球末位置的高度(相对于地面)d 每位队员发力为80N时所抓绳子末端的位置与牛皮双面鼓之间的竖直高度差d0 牛皮双面鼓处于运动状态中的任一位置与每位队员抓住绳子末端位置的竖直高度差d' 每位队员发力为90N时所抓绳子末端的位置与牛皮双面鼓之间的竖直高度差FN 每位团队成员对绳子所施加的拉力F合 在某个简化的单一方向上的合力W d-d'到d所做的功I排球下落速度与牛皮双面鼓上升速度的冲量v1 排球初始位置的速度v2 排球末位置的速度v3 排球与牛皮双面鼓发生碰撞后排球的瞬时速度v4 排球与牛皮双面鼓发生碰撞后牛皮双面鼓的瞬时速度V2 牛皮双面鼓在d-d'到d之间运动时的速度V3 排球与牛皮双面鼓发生碰撞前排球的瞬时速度V4 排球与牛皮双面鼓发生碰撞前牛皮双面鼓的瞬时速度α每位相邻团队成员所拉的绳子之间的夹角
3 问题分析
3.1 理想状态下鼓与球的运动情况
要研究团队的最佳协作策略,首先要清楚地分析出排球和鼓的运动(受力)情况。在理想状态下,不计空气阻力和排球与鼓面发生碰撞时所产生的摩擦力和弹力,并假设团队成员有8人,绳子长度为1.7m。球从鼓面中心正上方40cm处竖直落下进行自由落体运动(只受重力),鼓在受到人的拉力后上移,碰撞时产生的相互作用力促使球向上移动。而当队员们拉鼓,鼓与球碰撞结束后,使得球能够有最大的初始速度,这样一定会使得球被颠起的高度大于40cm,换言之便是实现尽可能多的连续颠球次数。由于问题涉及到力的方向、时机和力度,所以使用控制变量法转换变量来讨论最佳击球时机,将三维问题降级转换为二维问题来进行解决。
3.2 队员发力存在失误时鼓面的倾斜状态
通过表1中列出的每位团队成员不同的发力时机和力度,计算在0.1s时鼓面所产生的倾角。实际上是通过对鼓在不同状态下的受力分析(力的合成与分解),从而计算出牛皮双面鼓鼓面的倾斜角度。假设人为质点,已知鼓面的初始状态是水平静止的,此时鼓身周围的拉力将会处在一个保持平衡的状态。通过力的合成与分解,先统一每个力都相同,对俯视图中鼓受到的力进行分析,再将鼓受到的力合成竖直平面内的两个力,分别计算这两个拉力与水平方向的夹角。当拉鼓时的一个力发生变化,使用与平衡时的相同方法进行分析,计算出拉力和水平面的夹角后进而可计算出鼓的倾角。
3.3 球的弹跳发生偏移时球在鼓面的碰撞位置
当鼓面发生倾斜时,球的落点就会发生偏移而不会处于鼓面中心,以及鼓面倾斜的角度与队员拉绳子的力成反比。此时就需要队员调整拉绳的策略和队员的用力方向与力度。如果需要将球的运动状态调整为竖直的弹跳状态,需要团队成员调整鼓的位置使球与鼓面中心发生碰撞。当团队成员进行移动或发力去改变鼓的位置以及鼓面的平衡状态时,同时要考虑团队成员的移动速度和发力时机。当所有因素考虑周全且接近于最佳时,球最终将会在鼓面上竖直弹跳。
4 模型的建立与求解
4.1 理想状态下的最佳击球时机
4.1.1 定义最佳击球时机
当排球与鼓的碰撞过程完成后,如果排球获得了较大的上升速度,也就是说,在排球与牛皮双面鼓碰撞时排球能够获得最大的能量,由简单的物理原理,我们可以确定出排球在获取的能量最大时所上升的距离将成为排球可上升的最高高度。因为不同的碰撞时机会影响排球的上升高度,所以牛皮双面鼓的鼓面和排球冲量的改变也不同,由图1所示我们可以考虑牛皮双面鼓的鼓面和排球的碰撞关系。
4.1.2 分析理想状态下使得排球弹回至最大高度的碰撞时刻
图1中,由项目初始状态开始释放排球时,排球由鼓面中心正上方h=29cm处由静止状态开始竖直落下,假设排球的初末位置距离地面的高度分别为h1、h2,排球初末位置的速度分别为v1、v2。重力加速度为g,排球的质量为m,牛皮双面鼓的质量为M,牛皮双面鼓鼓面的弹性系数μ=0,根据动能守恒定律的表达式:

由式(1)可得排球在距离牛皮双面鼓鼓面的高度为h=h2-h1处的瞬时速度为:

同理可得知排球由牛皮双面鼓鼓面中心正上方h2=40cm处由静止开始竖直落下时开始计时,到第t时刻排球的瞬时速度:

又因为在项目开始之前需要每位队员用力拉绳使牛皮双面鼓保持静止状态。假设团队成员人数x=8人,绳子长度l=1.7m,每位队员抓绳子末端的位置与牛皮双面鼓中心的竖直高度差为d(规定牛皮双面鼓中心高于每位队员抓绳子末端位置为正,低于每位队员抓绳子末端位置为负),每位队员对绳子所施加的力FN=80N,每位队员拉的绳子之间的夹角为α。故牛皮双面鼓在项目开始之前处于静止状态下的受力情况俯视图如图2所示,侧视图如图3所示(视牛皮双面鼓为质点):

图2 静止状态下的受力情况俯视图
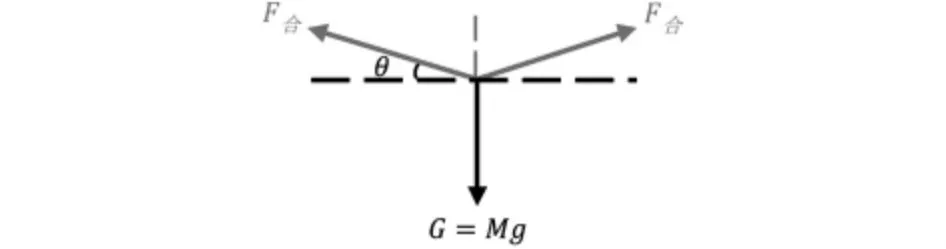
图3 静止状态下的合力受力情况侧视图
并且满足:

每位队员抓绳子末端的位置与牛皮双面鼓中心的竖直高度差:

牛皮双面鼓静止时绳子与水平面之间的夹角(F合为四位队员单侧方向的合力):

项目由初始状态开始释放排球时,排球由鼓面中心正上方h2=40cm处由静止状态开始竖直落下,且每位队员需要在各自作用力的方向上施加力的大小使牛皮双面鼓上升,并使牛皮双面鼓产生了竖直方向向上的加速度。假设当每位员对绳子所施加的力为F'N=90N时,且当牛皮双面鼓静止时,两侧队员的合力大小为:

F'N=90N时每位队员抓绳子末端的位置与牛皮双面鼓中心的竖直高度差d'为:

F'N=90N时牛皮双面鼓静止时绳子与水平面的夹角(F'合为四位队员单侧方向的合力):

假设队员在排球下落时拉绳的力由FN=90N瞬间变为F'N=90N的过程中,牛皮双面鼓在竖直方向向上做加速度逐渐减小的变加速运动,可得当F'N=90N时牛皮双面鼓在-d处竖直向上运动的瞬时加速度为:

当牛皮双面鼓竖直方向向上运动时,牛皮双面鼓在绳子的作用下做加速度逐渐减小的变加速运动,当牛皮双面鼓与每位队员抓绳子末端位置的高度差为d-d'时,牛皮双面鼓将做匀减速运动。故排球在牛皮双面鼓与每位队员抓绳子末端位置的高度差为d-d'到d之间与排球发生碰撞可使排球吸收的能量最大。牛皮双面鼓在d-d'到d之间运动时的速度为V2。设牛皮双面鼓处于运动状态中的任一位置与每位队员抓绳子末端的位置的竖直高度差为d0,可得出牛皮双面鼓在d-d'到d之间的功能关系:

当排球向下运动,且牛皮双面鼓向上运动时,排球下落速度与牛皮双面鼓上升速度的冲量值最大时,排球向上弹回的速度最大。设排球与牛皮双面鼓碰撞前的瞬时速度分别为v3,v4,排球与牛皮双面鼓碰撞后的瞬时速度分别为v'3,v'4。根据动量定理:

得出动量定理表达式:

根据动能守恒定律表达式:

动量定理表达式与动能守恒定律表达式联立,推导得:

进而与设定数据替换:

设牛皮双面鼓竖直向上运动的时间为tp,假设队员在排球下落时拉绳的力由FN=80N变为F'N=90N的过程中在t'时刻所用的力为FN0,由做功关系式:

可以得出队员在排球下落时拉绳的力由FN=80N逐渐变为FN0的过程中的平均作用力:

将式(13)、式(26)联立,可以得出牛皮双面鼓向上运动时在瞬时速度为V4时的时间t'p:

代入得:
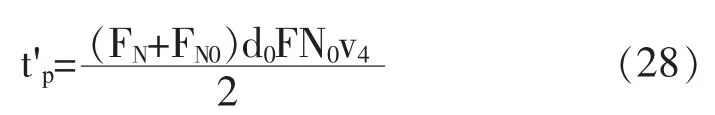
当排球与牛皮双面鼓碰撞后的瞬时速度v'3最大时,碰撞的时刻即为该团队的最佳协作时间。即可确定v3的最佳值,假设排球由项目开始时速度由v0开始计时到v3时的时刻为tq,代入式(3)得:

可推导出:

即当排球发出时开始计时,每位队员在排球发出后tq-t'p时刻同时增加力的大小拉动绳子可使排球弹回到最高点。当排球以v'3的速度弹回时,排球的颠球高度为最高。由速度-位移公式:

代入对应变量可得颠球高度H:

代入式(21)得:
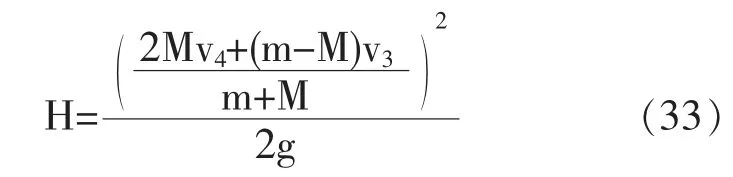
得出由排球发出时开始计时,每位队员在排球发出后的tq-t'p时刻同时增加力的大小拉动绳子可使排球弹到最高点H处。
4.1.3 实现最多的颠球次数的最佳协作策略
综合对排球的运动状态、牛皮双面鼓的运动状态、牛皮双面鼓的鼓面与排球的碰撞关系进行分析,由鼓面处于最佳速度时的运动状态得出排球与鼓面的最佳碰撞时刻t'p(如图4中所示),即为在理想状态下每位队员同时在tq-t'p时刻拉绳使得鼓面向上的速度最大时与排球碰撞后,排球弹回至最大高度以获得更大的重力势能来实现尽可能多的颠球次数。

图4 理想状态下牛皮双面鼓在一个周期内运动的速度-时间图像
4.2 现实情形中队员的发力时机和力度与某一特定时刻鼓面倾斜角度的关系
4.2.1 初始时刻鼓的状态
由于在项目开始前牛皮双面鼓的受力不会发生变化,且团队成员人数x=8,绳子长度l=1.7m,每位队员抓绳子末端的位置与牛皮双面鼓的竖直高度差d'=11cm,假设队员之间的距离均匀分布并且每位队员在项目开始之前对绳子所施加的力为FN=80N,则在初始时刻牛皮双面鼓受力均匀,同时鼓面处于水平静止状态。
4.2.2 特定时刻鼓面倾斜角度的论证
在项目开始时,每位队员各自保持恒定的发力方向拉绳使得鼓面具有向上的加速度,拉绳期间队员在对发力时机或发力大小的控制出现失误便会导致鼓面发生倾斜,并且鼓面的倾斜角度的大小因发力时机和每位队员所产生作用力大小的不同而受到不同程度的影响。由表1中的数据做如下分析:
Step1序号1求解
由式(4)的论证可知队员之间的夹角的为:

由式(5)的论证可知单侧队员的合力为:

由式(7)的论证可得出在项目开始之前牛皮双面鼓静止时绳子与水平面方向的夹角:

当其中一位队员在同一时刻内用力过大至FN=90N导致鼓面发生倾斜,需要对鼓的受力情况进行重新分析,如图5所示。
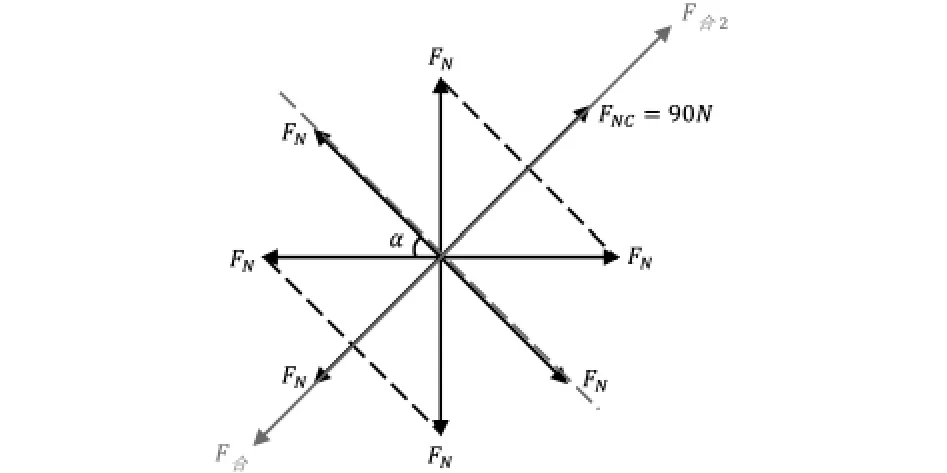
图5 一位队员用力过大至FN=90N导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向FNC方向升高并倾斜,对力进行分析的合力侧视图如图6所示:

图6 一位队员用力过大至FN=90N导致鼓面发生倾斜的合力受力情况侧视图
由受力分析图可得:
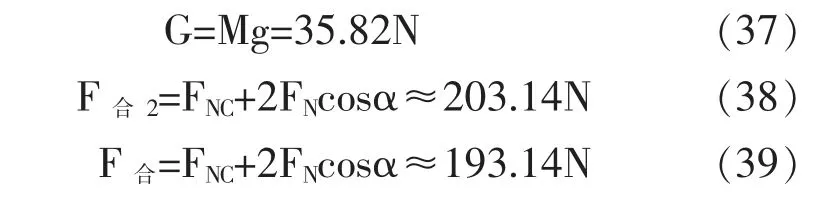
当F合2cosβ'=F合cosθ'且F合2sinβ'+F合sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:

解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向用力过大的队员方向向上倾斜。
Step2序号2求解
当其中两位相邻位置队员在同一时刻内用力过大至FN=90N导致鼓面发生倾斜,需对鼓的受力情况进行重新分析,如图7所示:
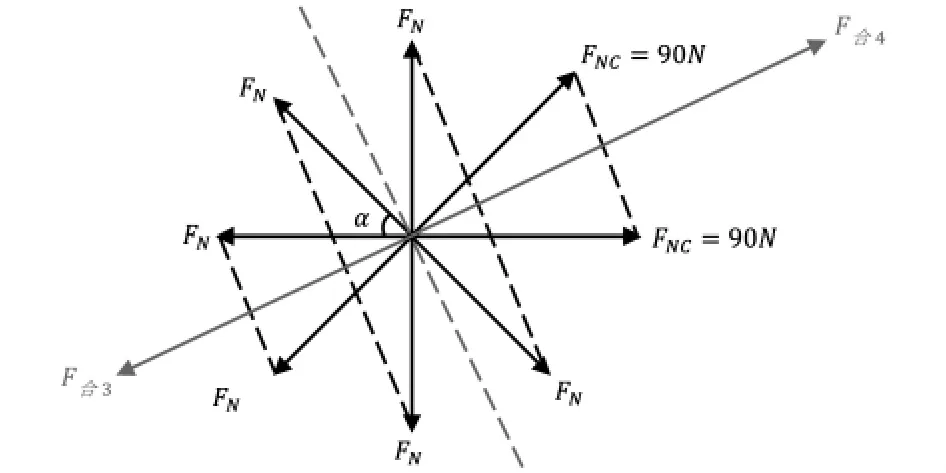
图7 两位相邻队员用力过大至FN=90N导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向F合2方向升高并倾斜,对力进行分析的合力侧视图如图8所示:

图8 两位相邻队员用力过大至FN=90N导致鼓面发生倾斜的合力受力情况侧视图
由受力分析图可得:
当F合4cosβ'=F合3cosθ'且F合4cosβ'+F合3sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:
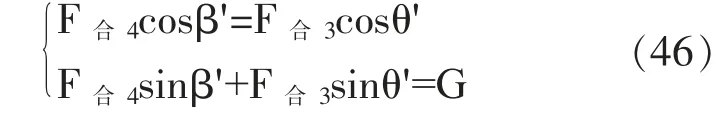
解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向用力过大的两位队员角平分线方向向上倾斜。
Step3序号3求解
当其中两位间二位队员在同一时刻内用力过大至FN=90N导致鼓面发生倾斜,需对鼓的受力情况进行重新分析,如图9所示:
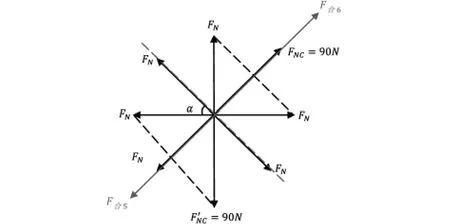
图9 两位间二位队员用力过大至FN=90N导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向FNC与F'NC夹角的角平分线方向升高并倾斜,对力进行分析的合力侧视图如图10所示。

图10 两位间二位队员用力过大至FN=90N导致鼓面发生倾斜的合力受力情况侧视图
由受力分析图可得:


当F合6cosβ'=F合5cosθ'且F合6sinβ'+F合5sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:
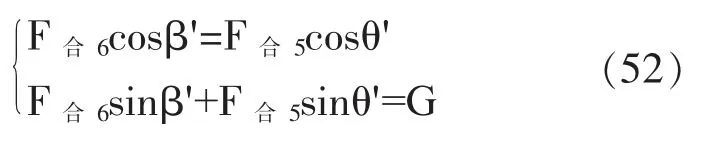
解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向两位队员夹角的角平分线方向向上倾斜。
Step4序号4求解
当其中一位队员在比正常情况下提前0.1s发出80N的力导致鼓面发生倾斜,需对鼓的受力情况进行重新分析,如图11所示:
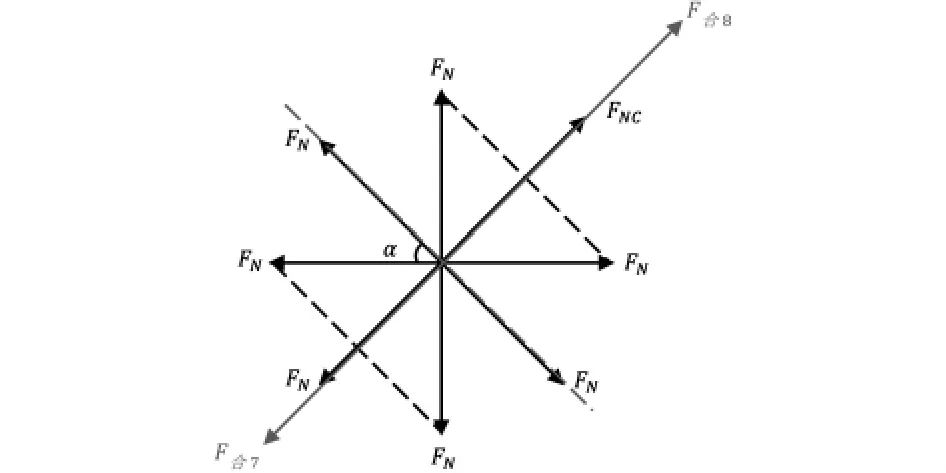
图11 一位队员提前0.1发出80N的力导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向FNC方向降低并倾斜,对力进行分析的合力侧视图如图12所示。
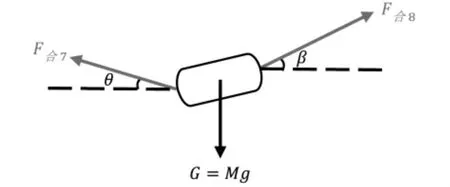
图12 一位队员提前0.1s发出80N的力导致鼓面发生倾斜的合力受力情况侧视图
由受力分析图可得:
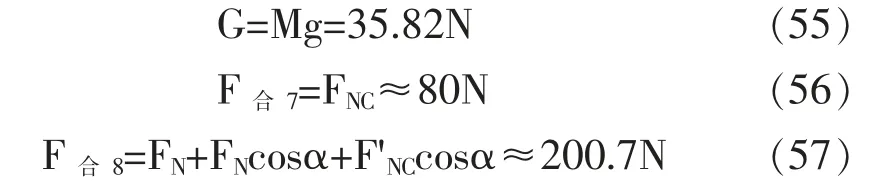
当F合8cosβ'=F合7cosθ'且F合8sinβ'+F合7sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:
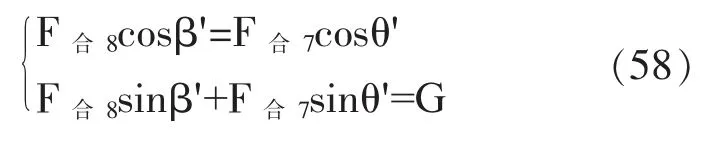
解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向提前出力的队员方向向上倾斜。
Step5序号5求解
当其中两位相邻队员在比正常情况下提前0.1s发出80N的力导致鼓面发生倾斜,需对鼓的受力情况进行重新分析,如图13所示:

图13 两位相邻队员提前0.1发出80N的力导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向FNC方向降低并倾斜,对力进行分析的合力侧视图如图14所示:由受力分析图可得:
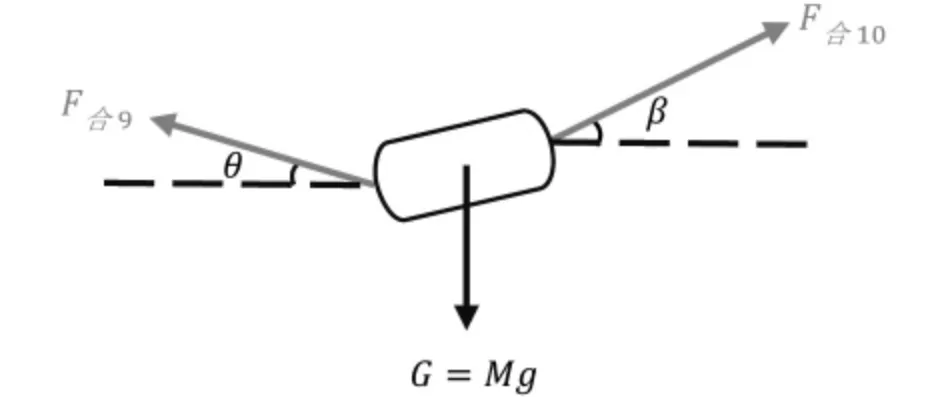
图14 两位相邻队员提前0.1s发出80N的力导致鼓面发生倾斜的合力受力情况侧视图

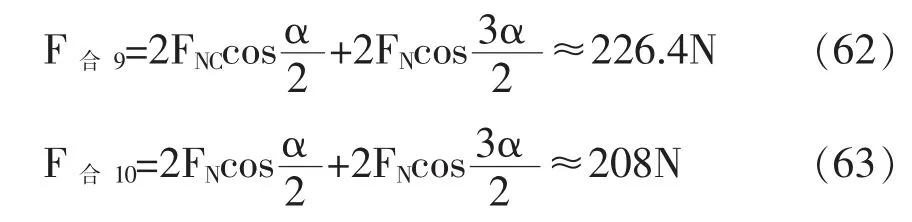
当F合10cosβ'=F合9cosθ'且F合10cosβ'+F合9sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:
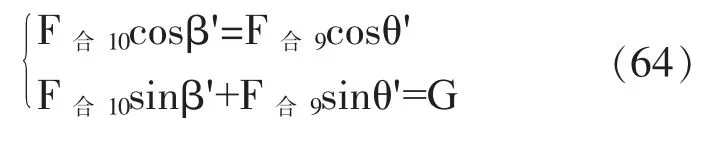
解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向提前出力的队员方向向上倾斜。
Step6序号6求解
当其中两位间二位队员在比正常情况下提前0.1s发出80N的力导致鼓面发生倾斜,需对鼓的受力情况进行重新分析,如图15所示:
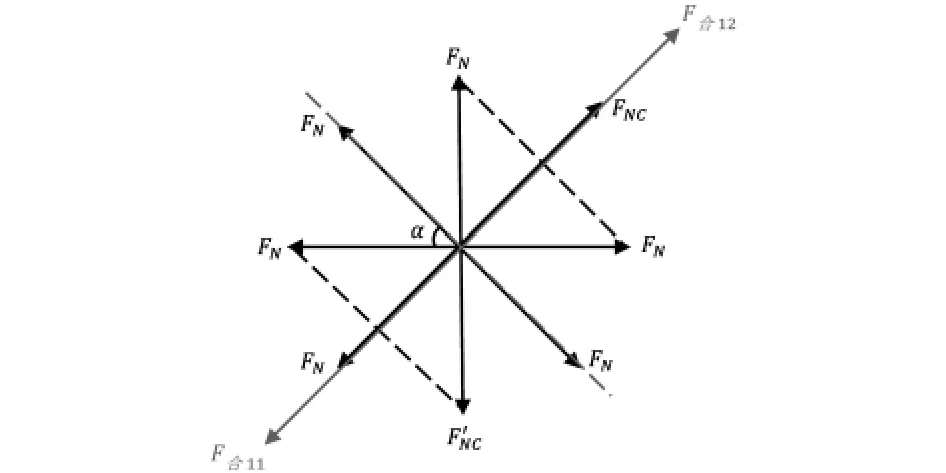
图15 两位间二位队员提前0.1s发出80N的力导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向FNC与F'NC夹角的角平分线方向升高并倾斜,对力进行分析的合力侧视图如图16所示:
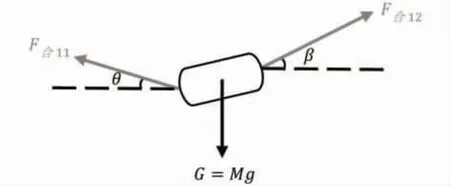
图16 两位间二位队员比正常提前0.1s发出80N的力导致鼓面发生倾斜的合力受力情况侧视图
由受力分析图可得:

当F合12cosβ'=F合11cosθ'且F合12sinβ'+F合11sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:
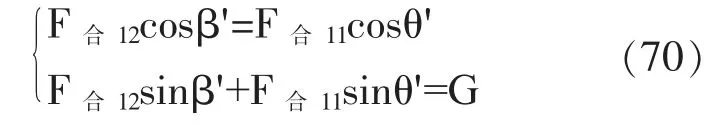
解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向提前出力的两位间二位队员夹角的角平分线方向向上倾斜。
Step7序号7求解
当其中一位队员在比正常情况下提前0.1s且用力过大至FN=90N导致鼓面发生倾斜,需对鼓的受力情况进行重新分析,如图17所示:
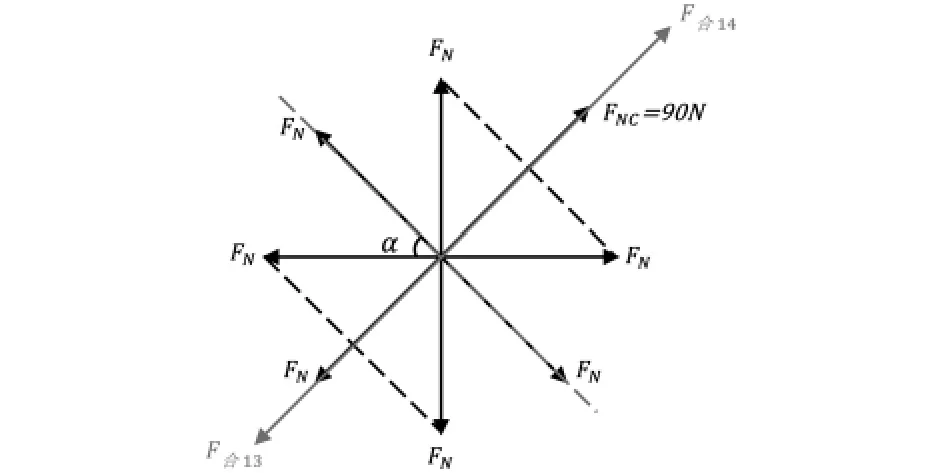
图17 一位队员提前0.1s发出90N的力导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向FNC方向升高并倾斜,对力进行分析的合力侧视图如图18所示:
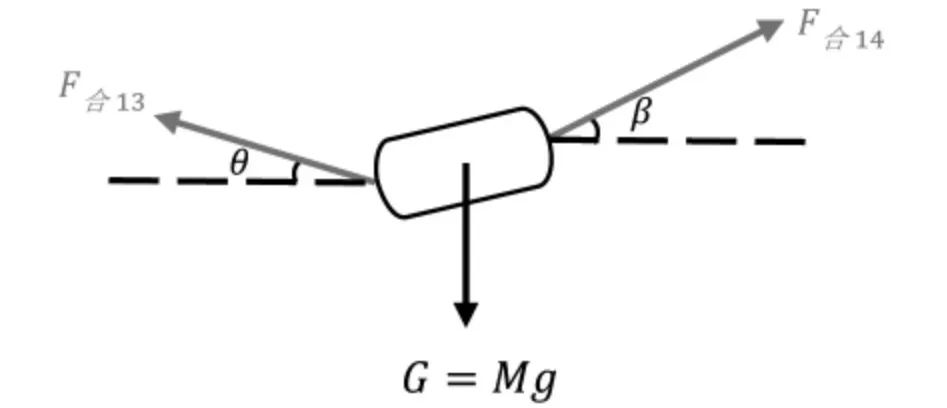
图18 一位队员提前0.1s发出90N的力导致鼓面发生倾斜的合力受力情况侧视图
由受力分析图可得:
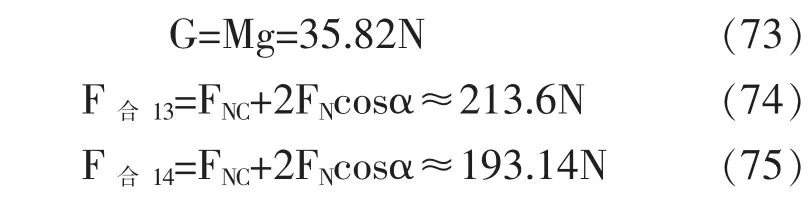
当F合14cosβ'=F合13cosθ'且F合14sinβ'+F合13sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:

解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向用力过大的队员方向向上倾斜。
Step8序号8求解
当其中两位间二位队员在比正常情况下提前0.1s且与之交叉相邻的其他两位队员在比正常情况下用力过大至FN=90N导致鼓面发生倾斜,需对鼓的受力情况进行重新分析,如图19所示:

图19 两位队员提前0.1s用力且交叉相邻的两位队员增加10N导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向F合16方向升高并倾斜,对力进行分析的合力侧视图如图20所示:

图20 两位队员提前0.1s用力且交叉相邻的两位队员增加10N导致鼓面发生倾斜的合力受力情况侧视图
由受力分析图可得:

当F合16cosβ'=F合15cosθ'且F合16sinβ'+F合15sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:

解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向为向F合16方向向上倾斜。
Step9序号9求解
当其中两位间二位队员在比正常情况下提前0.1s且与之对向相邻的其他两位队员在比正常情况下用力过大至FN=90N导致鼓面发生倾斜,需对鼓的受力情况进行重新分析,如图21所示:
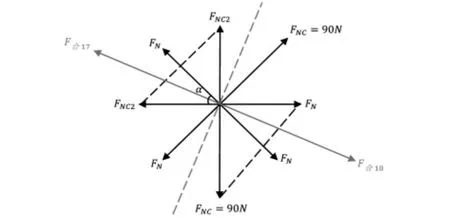
图21 两位队员提前0.1s用力且对向相邻的其他两位队员增加10N导致鼓面发生倾斜的受力情况俯视图
可以得知鼓面向F合16方向升高并倾斜,合力侧视图对力进行分析如图22所示:

图22 两位队员比正常提前0.1s用力且对向相邻的其他两位队员增加10N导致鼓面发生倾斜的合力受力情况侧视图
由受力分析图可得:
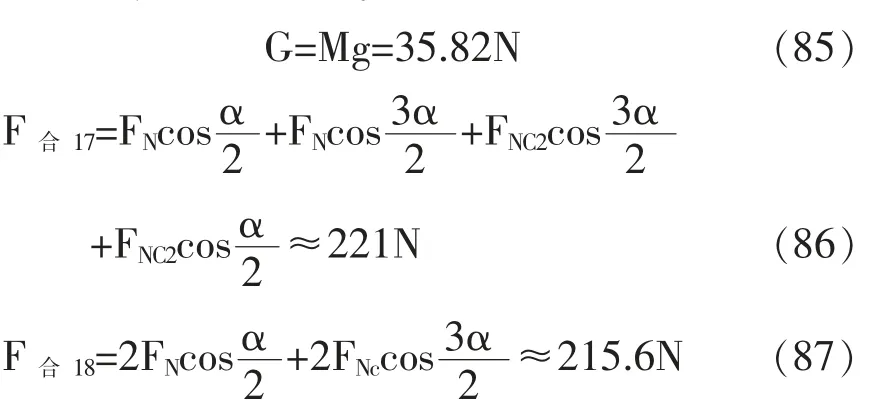
当F合17cosβ'=F合18cosθ'且F合17cosβ'+F合18sinθ'=G时,鼓将会恢复平衡状态,联立上述两式:
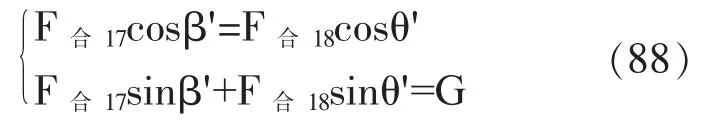
解得:

设鼓面倾斜角为γ,可由β'和θ'计算当有一位队员用力过大时鼓面的倾斜角度:

故在0.1s时鼓面倾斜方向为向F合17方向向上倾斜。
4.2.3 使得鼓面倾斜角度最小的论证结果
通过上述计算及论证得出的结果,在实际情形中每位团队成员在不同的发力时机和发力大小情况下所得出的鼓面倾角如表3所示。
由表3中得出鼓面倾角的数据和图23中的3D颜色映射曲面图可知,在现实情形中团队成员对绳子的控制存在一定误差导致鼓面出现倾斜状态时,当所有队员同时发力并且仅有两位相邻队员增加10N的力时,鼓面产生的倾斜角度最小。

表3 发力时机(单位:s)和用力大小(单位:N)取值得出的鼓面倾角
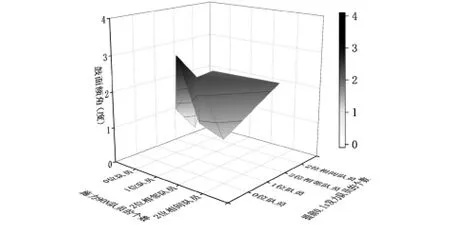
图23 鼓面倾斜角度与不同队员个数出现误差情况时的3D颜色映射曲面图
4.3 鼓在倾斜状态下调整鼓使球保持竖直弹跳状态的策略
4.3.1 排球的弹跳方向发生偏移后鼓的调整策略
当鼓面产生倾斜状态时,排球与鼓面发生碰撞后,排球的跳动方向发生偏移,需要每位队员协作对各自的力进行调整,从而使排球与竖直方向产生夹角。假设参加该项目的团队成员一共有10人,绳子的长度为2m,排球与鼓面发生碰撞后所反弹的高度为60cm,同时产生相对于竖直方向偏移1°的倾斜角。通过队员对各自的发力时机和力度进行控制使鼓面具有与球运动方向相反的偏移方向、让鼓面中心与排球发生碰撞,实现使排球逐渐趋于竖直的弹跳状态最终达到稳定竖直向上弹的效果。
4.3.2 寻找排球与鼓面的位置关系
在排球与鼓面发生碰撞后,排球反弹高度为60cm时排球与鼓面之间的关系如图24所示。
由图24可知,当排球弹回后需调整鼓的位置与角度,需要两名队员施力移动牛皮双面鼓至排球竖直下落中心,使得排球可以获得最大的弹回速度。

图24 发生碰撞后排球高度为60cm时排球与鼓面之间的关系图
4.3.3 鼓面的最佳击球位置
依据对牛皮双面鼓鼓面的弹力示意图可以得出排球下落时与鼓面发生碰撞的最佳位置,如图25所示(颜色越浅表示的弹力越大,即为排球与鼓面的最佳碰撞位置):
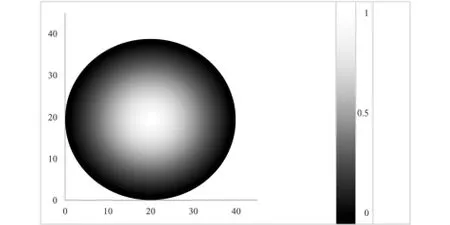
图25 牛皮双面鼓鼓面弹力示意图
当牛皮双面鼓与排球发生碰撞前,牛皮双面鼓在队员的共同作用力下使得鼓面中心与排球发生碰撞时使排球产生最佳上弹速度,同时鼓面向与排球相反的倾斜方向进行倾斜可使得排球逐渐趋向于竖直弹跳的状态,最终达到稳定竖直方向弹跳的效果。
5 总结
通过对排球与鼓面发生碰撞后的运动状态分析,运用基础力学与能量动力学知识,得出在理想状态下控制牛皮双面鼓使排球与鼓面发生碰撞后,产生最佳弹起角度与高度,以此得出对应的拉绳时间以获得最大颠球次数。同时讨论了现实情况下,因队员发力大小和发力时机出现失误时,使鼓面倾角迅速恢复至最小的协作方法,由此使排球的弹跳状态快速恢复到竖直弹跳状态,最终实现最多的击球次数。
——鼓

