基于约束投票极限学习机的在线静态电压稳定评估

汤迎春，晏光辉，张雅婷，刘书池，刘颂凯，张磊

（1. 国网孝感供电公司, 湖北省孝感市 432000；2. 三峡大学电气与新能源学院, 湖北省宜昌市 443002）

0 引言

随着可再生能源的持续增长和现代电力系统的广域互联，电力系统的安全稳定运行面临着前所未有的挑战。由于电压崩溃可能会造成巨大的经济损失，并对社会生活和工业生产产生不可预测的负面影响，因此，实时监测电力系统运行状态，进行即时的静态电压稳定评估已经成为维护系统安全运行的关注热点。

静态电压稳定是指系统受到小干扰后母线电压维持稳定的能力。对于系统运行人员而言，获取电力系统初始运行点到电压崩溃点的“距离”对于静态电压稳定评估尤为重要。通常，这个“距离”可以用电压稳定裕度（voltage stability margin，VSM）表示。目前，存在多种获取VSM的方法，如灵敏度法、奇异值分解法和连续潮流法（continuation power flow，CPF）[1-2]。由于现代电力系统结构愈发复杂，运行规模逐渐增大，传统分析方法需要消耗大量计算时间和计算资源，难以保证静态电压稳定评估的实时性和有效性[3-4]。

随着广域测量系统的发展与应用，电力系统运行数据能被更加快速、精准地采集，这为实现在线静态电压稳定评估提供了极大的便利。因此，一些数据驱动方法被引入了电压稳定评估领域，如人工神经网络（artificial neural network，ANN）[5-6]、支持向量机（support vector machine，SVM）[7]、决策树（decision tree，DT）[8]等。其中，ANN调参过程繁杂，训练耗时较长，模型训练效率较为低下；SVM算法在大规模训练样本上的训练效率制约着其在电力系统领域的进一步发展；DT对于样本数据中的噪声过于敏感，并且容易出现过拟合问题。

近年来，极限学习机（extreme learning machine，ELM）的提出使得单隐藏层神经网络备受关注。ELM在训练过程中随机生成输入-隐藏层权值及神经元偏置项，只需设置适当的隐藏层节点数，即可获得最优输出权值，这使得ELM相较上述算法而言具有高效的学习效率及优异的泛化性能。但是，随机选择网络参数会影响ELM性能。比如在实际应用中，合适的隐藏层节点数往往在一个相对狭窄的范围内，随机设置过多或过少的节点数可能会使得网络模型因结构冗余而过拟合或者因结构简单而无法达到预期的训练效果。

针对上述问题，本文提出一种基于约束投票极限学习机（constrained voting extreme learning machine，CV-ELM）的在线静态电压稳定评估方法，利用类间样本差值构成差向量集，根据选取的差向量计算输入层对隐藏层的权值及隐藏层节点偏置项，由此构造多个独立ELM进行集成学习，并采用多数投票机制进行最终决策。仿真结果表明，本文提出的静态电压稳定评估模型具有良好的泛化能力，并且模型评估精度优于传统机器学习方法。

1 CV-ELM算法

1.1 ELM

ELM本质上是一种广义单隐藏层前馈网络，如图1所示，其包含3层网络结构：输入层、隐藏层、输出层[9]。

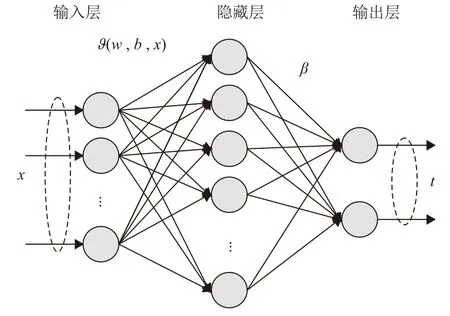
图1 单隐藏层前馈网络结构Fig. 1 Structure of single-hidden-layer feed-forward network

给定一个包含N个样本的训练数据集，其中xj是一个n×1的输入向量；tj是一个m×1的 目标向量；有个隐藏节点的单隐藏层前馈网络的输出函数如式（1）所示

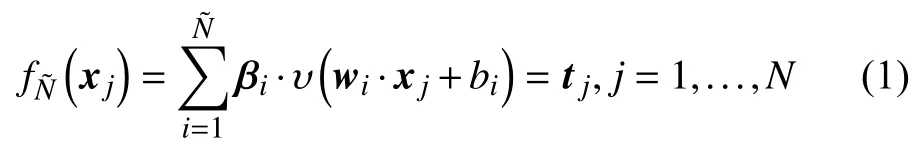
式中：υ为激励函数；wi是连接第i个隐藏节点和输入节点的权重向量；βi是连接第i个隐藏节点和输出节点的权重向量；bi是第i个节点的偏置；wi·xj表示wi和xj的内积。

ELM通过随机选择隐藏节点的输入权重w和偏置b，并直接进行矩阵计算确定输出权重β。根据ELM理论，公式（1）可以被简化为

式中：H代表网络的隐藏层输出矩阵。

在训练数据集上，给定激励函数和隐藏节点数，ELM的学习过程可以概括为3个主要步骤：

1）对于i=1,...,，随机生成输入权重wi和偏置bi；

2）计算隐藏层输出矩阵H；

3）计算输出权重矩阵β=H†T,其中H†是H的穆尔-彭罗斯广义逆矩阵，可以通过奇异值分解计算得到[9]。

1.2 约束参数设定

实际上，输入权值的本质是将样本数据从原始样本空间映射到另一个特征空间，便于模型对样本学习并分类，当输入层到隐藏层的权值矩阵完全随机生成时，样本在新空间中的映射极有可能发生规模化散乱，这将严重影响模型对样本的学习及后续的分类。

根据类间样本组成的差异向量构造隐藏层参数，能够使得样本从原始空间到新特征空间中的映射具有一定规律性，以便提升后续分类精度。

以xl1代 表一个正例样本，其标签为l1；xl2为一个反例样本，其标签为l2 。α为输入层到隐藏层的权值矩阵，可以表达为：

式中：λ为归一化因子。单隐藏层神经网络输入输出关系，可以表达为

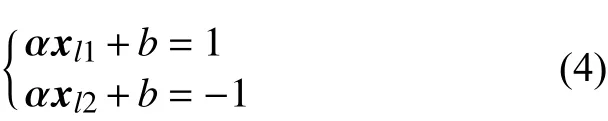
式中：b为 隐藏层节点偏置项，根据α 与λ的关系，式（4）可以进一步表达为：

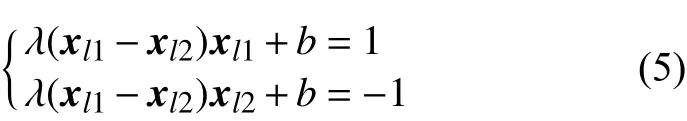
则归一化因子λ和偏置项b可以根据（5）反推得到：

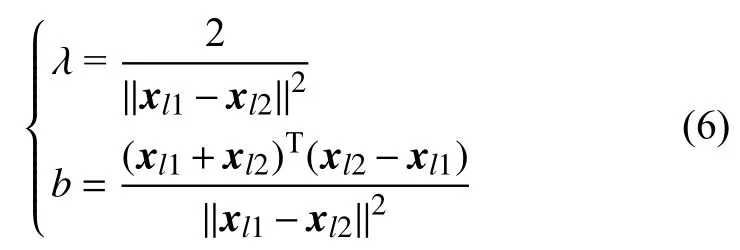
因此，输入层到隐藏层的权值矩阵α可以根据正反例样本的差异向量求取：

根据以上分析所得公式，权值矩阵α通过样本类间差异向量选取，有效避免了样本映射散乱导致的后续分类精度下降问题。基于上述过程，可获得由ELM改进后的约束化极限学习机（constrained extreme learning machine，C-ELM）。

1.3 多数投票机制

改进后得到的单个C-ELM在处理处于分类二值边界附近的样本时存在误分类情况。因此，本文提出CV-ELM集成框架，建立多数投票机制，以有效遏制误分类率，即训练多组C-ELM，对于输出结果存在差异的样本，采用“少数服从多数”机制，选取占比较多的分类结果作为该样本最终的分类结果。

1.4 CV-ELM训练框架

预先设定CV-ELM中C-ELM的数目为M，计算M组样本类间差异向量，每个C-ELM分配一组样本类间差异向量，计算其输入层到隐藏层之间的权值矩阵及隐藏层神经元偏置项，然后遍历所有样本进行学习，最后在测试集上进行测试验证。CV-ELM整体训练框架如图2所示。

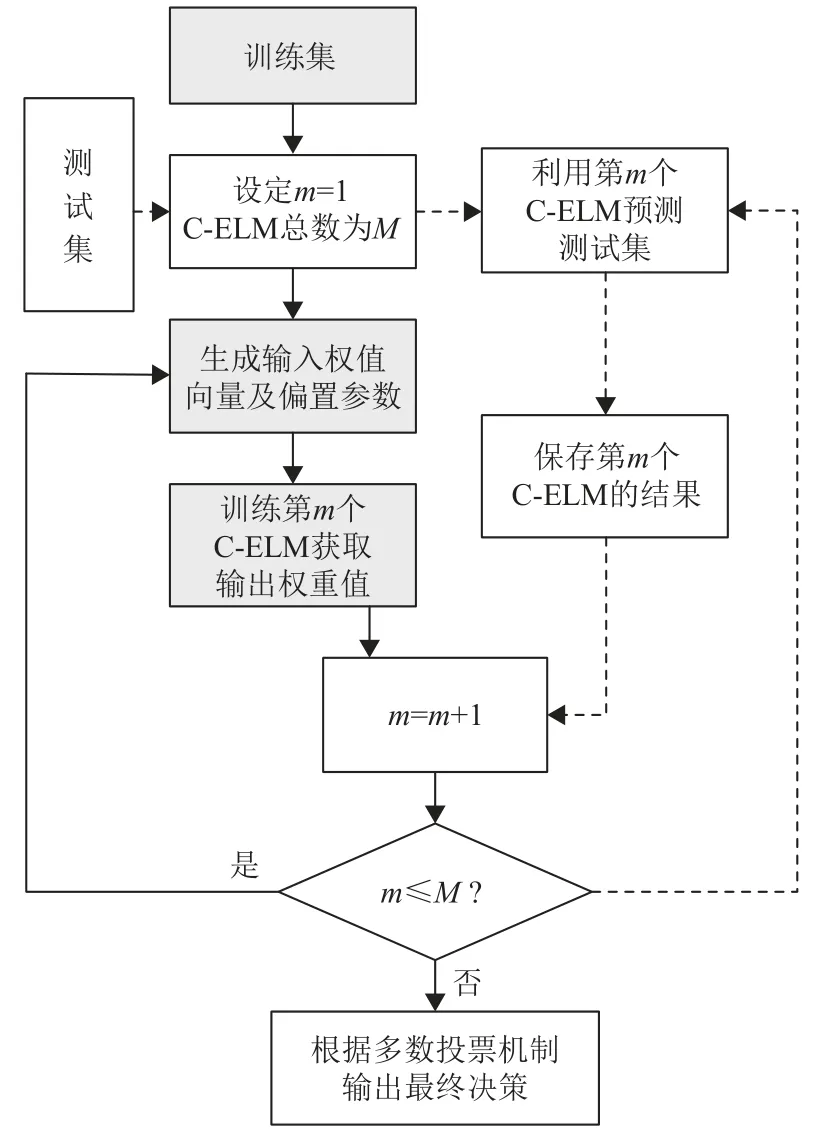
图2 CV-ELM训练框架Fig. 2 Training framework of CV-ELM algorithm

2 在线静态电压稳定评估模型构建

本文所提出的基于CV-ELM的在线静态电压稳定评估流程如图3所示，并主要包含2个阶段：离线训练与在线评估。

图3 在线静态电压稳定评估流程Fig. 3 Flow chart of online static VSA

2.1 静态电压稳定指标

对于静态电压稳定而言，P-V曲线常被用于描述负荷节点电压与负荷有功功率之间的关系。随着负荷需求的改变，负荷节点电压幅值的变化如图4所示。其中：P0代表某一电力系统运行点A的负荷有功功率；Pmax代表电压崩溃点B的最大负荷有功功率。当前运行点A与电压崩溃点B的有功功率差可用ΔP表示，如式（8）所示。

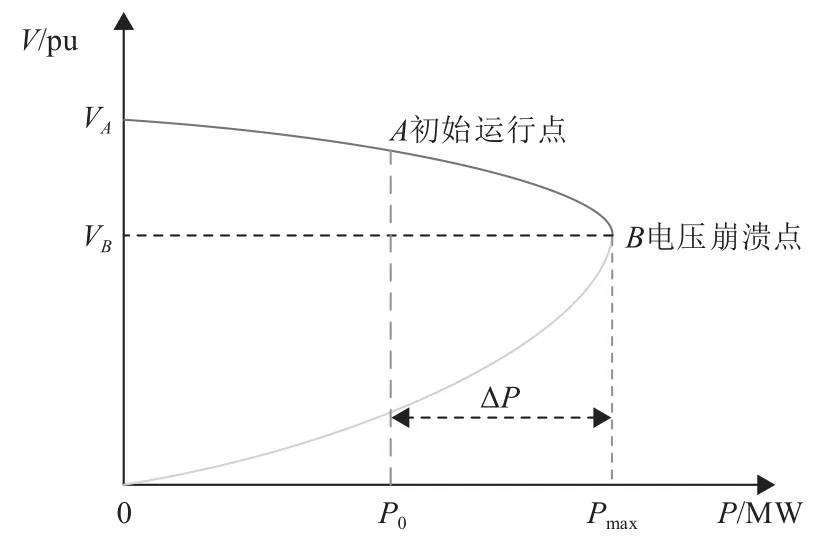
图4P-V曲线示意图Fig. 4 Schematic diagram of P-V curve

当电力系统处于电压崩溃点时，潮流雅克比矩阵奇异，无法收敛，电压稳定达到极限[10-11]。本文基于ΔP定义连续性VSM指标，如式（9）所示。

2.2 离线训练

在离线训练阶段，首先依据VSM指标确定原始数据的标签，结合大量系统仿真/历史运行数据，建立离线数据库。在稳定运行范围内初始化负荷、发电机以及分流器的运行数据，通过连续潮流仿真获取一系列运行点，记录运行点数据，计算其对应的VSM，即可生成一组初始数据。

为处理数据特征量庞大带来的“维数灾”，需要高效的特征选择方法，本文采用基于套袋最近邻预测独立性检验（bagging nearest-neighbor prediction independence test，BNNPT）[12]和 皮 尔逊相关系数[13]的特征选择方法。该方法利用BNNPT分析特征与VSM之间的非线性关系，结合皮尔逊相关系数分析特征与VSM之间的线性关系，综合考虑非线性和线性相关性，筛选出与VSM高度相关的关键特征，以此有效削减样本维度，避免特征过多导致的“维度灾”。根据所选关键特征和相应的VSM建立离线数据库。

利用关键特征和相应的VSM作为训练CVELM的输入和输出，对模型进行离线训练，建立电力系统运行数据与VSM之间的映射关系。

2.3 模型更新

离线训练的模型可能无法适应由于系统中负荷分布变化、发电机出力分布变化、拓扑变化等不确定性因素带来的影响[14-15]。为了提高评估模型的泛化能力，实现精确的在线评估，还须设立模型更新机制应对系统运行工况的潜在变化。

模型更新过程如图5所示。通常，可从电网公司获得故障列表，在离线阶段为每个故障准备一组CV-ELM评估模型。在线应用时，若变更的运行工况已被包含在离线数据库中，则选取对应的训练好的CV-ELM模型代替当前模型进行电压稳定评估；否则将使用离线阶段准备的所有评估模型对新的系统运行工况进行评估。若可以提供较为准确的评估结果，则选取性能最好的评估模型；否则需要基于该故障建立对应的训练数据集训练新的CV-ELM评估模型。需要说明的是，模型更新是一个长期的过程。实际上，根据电力系统日前或小时前调度计划，系统运行人员可以预测未来一段时间内的电力系统运行工况，在此过程中，如若遭遇数据库中未计及的工况变化，系统运行人员有充足的时间根据未计及的潜在运行工况训练相应的CV-ELM评估模型来实现模型的更新。从长远的角度而言，随着模型更新过程的不断执行，离线数据库中未计及的运行工况将不断减少，最终能实现无缝的在线电压稳定评估。

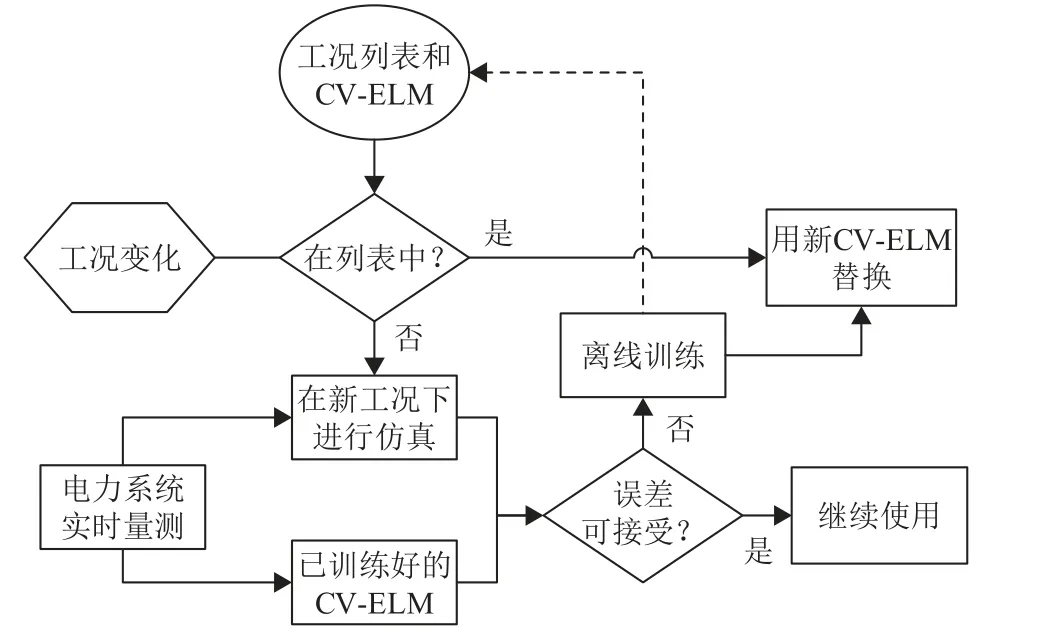
图5 模型更新示意图Fig. 5 Schematic diagram of model updating

2.4 在线评估及评估指标

当广域量测系统（wide area measurement system，WAMS）服务器接收到实时相量测量单元（phasor measurement unit，PMU）的测量信息，关键特征数据将被立即筛选出来并发送到相应的CV-ELM评估模型，模型将实时提供对电力系统当前运行状态的评估结果。

本文采用准确率（P）、召回率（R）及F1评分等性能指标评价所提模型的性能。

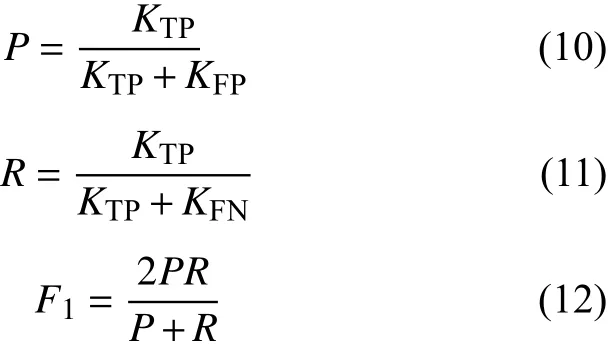
式中：KTP为分类结果中的真正样例；KFP为假正样例；KFN为假反样例；P表示所有被分类为正样例的样本中真正样例所占比例；R表示所有实际正样例中被正确分类的样例；F1综合了二者的结果，当F1较高时，表明分类结果较为理想[16]。

3 算例仿真与分析

为验证本文所提方法的有效性和准确性，以图6所示的新英格兰10机39节点系统作为测试系统，进行仿真测试。

图6 新英格兰10机39节点系统图Fig. 6 Diagram of New England 10-machine 39-bus system

3.1 数据生成

采用基于CPF的数据生成方法，生成大量的样本数据。为了模拟负荷分布的不确定性，将新英格兰10机39节点系统的每个负荷视为一个符合正态分布的概率密度函数的随机变量，设置概率密度函数的标准差为基准负荷水平的15%并多次取值，当所有负荷的初始值确定后，发电机初始输出功率由最优潮流确定。

为了获取更多的样本数据，在发电机初始输出中添加合理的波动，以考虑发电机的出力变化。在功率因数不变的情况下，将负荷初始值在70%~130%范围内改变，模拟负荷水平变化。最终生成了4270个样本。本文采用5折交叉验证法进行下述算例分析。

3.2 模型性能测试

3.2.1 计算耗时对比测试

在电力系统实际运行中，WAMS系统所安装的PMU装置对电网运行数据的采集频率高于30次/s。为了实现实时电力系统电压稳定评估，PMU数据的处理时间必须少于0.033 s。为验证本文所提方法的时效性，将其与传统的电压稳定评估方法（直接法[17]和连续潮流法）进行对比测试，计算时间对比如表1所示。

表1 不同方法的计算时间结果Table 1 Computation time results by different methods

由表中数据可知，使用直接法和连续潮流法进行电压稳定评估所需时间远大于本文所提方法，并且其单个样本计算时间分别为0.034 s和0.218 s，均高于PMU数据采集速度，因此直接法和连续潮流法难以及时有效地处理PMU所采集的数据，无法保证在线电压稳定评估的时效性。相比于直接法和连续潮流法，本文所提方法在计算时间方面具有明显的优势，避免了复杂的迭代潮流计算和非线性方程组求解的过程，总体计算时间仅为1.530 s，且单个样本计算时间远低于PMU数据所需最小处理时间，可快速处理PMU所采集的海量数据。因此，本文所提出的方法可以对电力系统电压稳定状态进行实时评估。

3.2.2 隐藏层节点数量测试

随机选取80%的初始样本对ELM、CV-ELM、C-ELM进行训练，利用剩余20%的样本对3种模型进行测试，隐藏层节点个数设置为20~400，对比结果如图7所示。

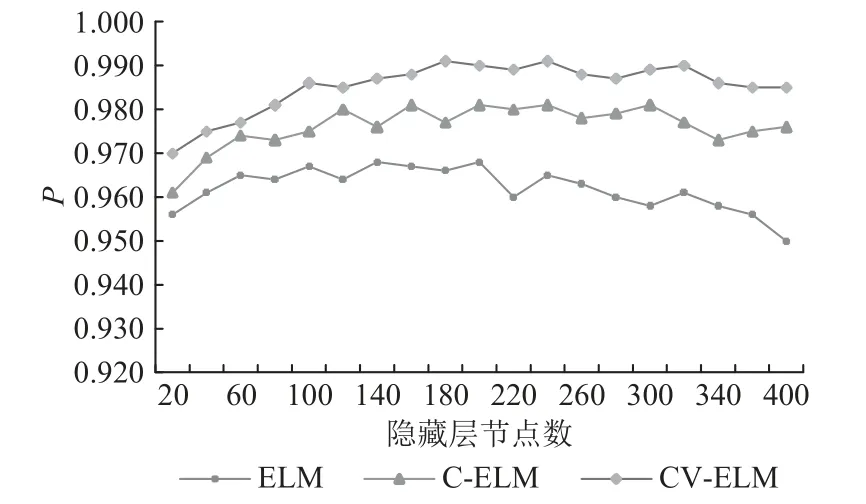
图7 隐藏层节点数对准确率的影响Fig. 7 Influence of the number of nodes in hidden layer on the accuracy

图7中的测试结果表明，当隐藏层节点数在20~200的范围内，ELM、C-ELM和CV-ELM的分类精度总体上随隐藏层节点数量的增加逐渐上升，之后，随着隐藏层节点数量进一步增加，ELM与C-ELM的分类精度均存在下降趋势，其中ELM的下降趋势尤为显著，而CV-ELM在节点数70~350时，其分类结果均有较好的精度，且随着隐藏层节点数量进一步增加，CV-ELM分类精度下降趋势也不明显。可见，在根据类间样本组成的差异向量构造隐藏层参数的前提下，CELM分类精度相较于ELM有显著提升，在多数投票机制与前者的共同促进下，CV-ELM的分类精度进一步得到提升，且多隐藏层节点下的泛化性能相较传统ELM有显著提升。

3.2.3 训练集规模的影响

为测试训练集规模对CV-ELM评估性能的影响，本文利用5种不同规模的训练集（40%、55%、70%、85%和100%的初始训练集）对具有180个隐藏层节点CV-ELM模型进行离线训练，并对同一组测试集进行测试，相应的测试结果如表2所示。

从表2可见，在训练集规模较小时，CVELM的分类精度仍然能保持在相对较高的水平，相比于深度神经网络结构，ELM的单层神经网络不具备复杂的结构，即使在训练样本数据不足的情况下，也不会受到局部离群点或者噪声数据的影响而出现过拟合现象，同时，CV-ELM的集成化结构进一步提升了模型的分类准确率。因此，综上可知，CV-ELM在相对小规模样本数据下依然能够保证较高的分类精度和泛化能力。

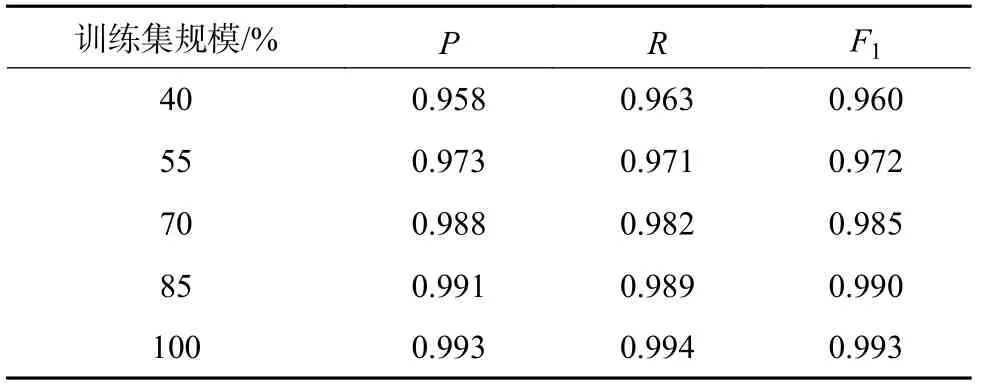
表2 不同训练集规模的测试结果Table 2 Test results of different training set sizes

3.2.4 与其他数据驱动方法的对比

为了进一步验证本文所提方法的优越性，将CV-ELM与传统的ANN、SVM和DT进行性能对比。其中设置CV-ELM隐藏层节点数为180；SVM采用径向基核函数（radial basis function，RBF），惩罚因子C设置为100，核参数设置为4；DT采用C4.5算法，最大深度为10。测试结果如图8所示。

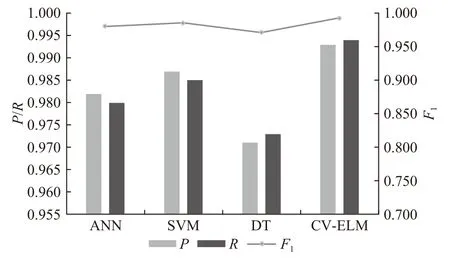
图8 不同数据驱动方法的对比结果Fig. 8 Contrast results of different data-driven methods

由图8可见，CV-ELM较传统的ANN、SVM、DT等算法，在分类准确率(P)、召回率(R)、F1指标等方面均体现出较为显著的优势。

3.2.5 模型抗噪性能对比

考虑实际系统中，样本数据容易产生噪声，本文对CV-ELM与其他传统常规算法进行了抗噪性能试验对比。

基于IEEE C37.118标准，PMU的量测误差应保持在1%的范围以内。通常，20dB的信噪比相当于数据中含有1%的噪声。本文为了验证CVELM在不同数据噪声环境下的鲁棒性，向数据中添加了信噪比范围40~10dB的高斯白噪声，对应 数据噪声范围约为0.01%~3%，其对比结果如图9所示。

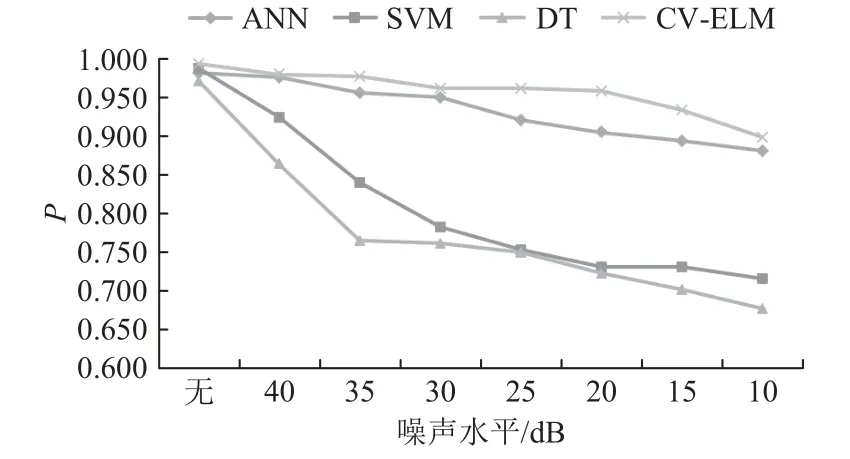
图9 模型抗噪能力对比Fig. 9 Comparison of anti-noise property of different models

由图9对比结果可知，在数据中加入不同程度的噪声后，CV-ELM、ANN、SVM和DT等模型分类准确率均受到不同程度影响，其中，SVM与DT的准确率随着噪声水平增加而下降的趋势尤为明显，ANN对噪声有一定的鲁棒能力，但相比之下CV-ELM对噪声的鲁棒性能更强，尽管CV-ELM仍受到噪声的影响，但其准确率并未出现明显下降，且整体准确率高于其他3种算法。

4 结论

1）基于新英格兰10机39节点系统的测试结果表明，本文所提出的方法可保证在线静态电压评估的时效性。

2）隐藏层节点数对分类精度影响对比显示出CV-ELM较于单个C-ELM在分类精度上有明显提升，并且在多隐藏层节点下，CV-ELM模型泛化性能亦优于前者。

3）即便在数据样本不足的情况下，CVELM也能维持较为可观的分类精度，不会出现严重过拟合现象。

4）随着噪声水平的增加，CV-ELM评估性能相较其他算法更加稳定，显现出更强的鲁棒性。