一种利于工程应用的快速反卷积波束形成方法

张 铮，徐雅南，孔 强

(杭州应用声学研究所，浙江杭州 310023)

0 引言

阵列信号处理作为现代信号处理的重要组成部分，被广泛应用于声呐、雷达中。水平线列阵作为一种基本阵型，是声呐系统中的一个重要组成部分。在传统的声呐系统中，通过常规波束形成(Conventional BeamForming,CBF)处理来获得阵增益，提高目标探测能力。但是，CBF主瓣波束宽度宽、旁瓣级高，降低了其空间分辨能力，在多目标时容易产生混叠，对有强干扰的弱目标检测能力较弱。为了提高空间分辨能力，一批高分辨波束形成算法被提出，比如最小方差无畸变响应法(Minimum Variance Distortionless Response,MVDR)[1]、最大熵法[2]、主模式抑制法(Dominant Mode Rejection,DMR)[3]、多信号分类法(Multiple Signal Classification,MUSIC)[4]、基于旋转不变技术的信号参数估计法(Estimating Signal Parameter Via Rotational Invariance Techniques,ESPRIT)[5]等。但是，这些方法在提高了分辨力的同时，也有其使用限制。如对阵型精度要求高、需要较多数据构建协方差矩阵、计算量大、稳定性差[6]等。

为了获得兼顾高分辨能力和稳定性的波束形成算法，人们开始将其他学科的成果应用到阵列信号处理中来。反卷积算法起初多应用于图像处理领域[7-8]，用于提高图像分辨率，Yang将反卷积算法与常规波束形成结合，提出了一种稳健的高分辨波束形成算法，并通过水平线列阵[9]和圆阵[10]对反卷积波束形成的稳定性、分辨力和处理增益进行了仿真研究和实验验证，结果表明，该方法具有和CBF一样的稳定性，与MVDR等高分辨波束形成算法分辨能力相近，并且提供了一定的处理增益。

尽管文献[9]的反卷积波束形成算法具有稳健、分辨力高和提高处理增益的优点，但在工程应用中还会面临一些实际问题。以水平线列阵声呐为例，通常工作在一个较宽的频带内，而反卷积算法中用到的阵列波束图也可称作阵列的点扩散函数(Point Spread Function,PSF)与频率有关，较宽的频带即意味着需要计算更多频点的PSF，增加了计算量；文献[9]中使用基于Richardson-Lucy(R-L)迭代算法的反卷积波束形成算法，因为信号截断，在波束图的两端会有边界模糊问题。反卷积波束形成可以看成是在CBF的基础上进行反卷积处理的算法，因此其计算量高于CBF。如何降低该方法的计算量，将计算量增加部分控制在一个可接受的范围内，是工程实践中需要解决的实际问题。本文对以上工程应用中的问题进行分析、讨论和优化，提出了一种利于工程应用的快速反卷积波束形成方法。

1 利于工程应用的快速反卷积波束形成方法

1.1 均匀线阵常规波束形成

以一个具有N个阵元的水平线列阵为例，阵元间距为d，声源在远场，声信号以平面波形式到达各阵元，信号的入射方向为θ，如图1所示。入射信号以R=AiPi+Ns表示，其中i为目标计数，Ai为第i个目标信号强度，为第i个目标在各阵元的相移向量，其中p定义如下pin=exp[- jk(n-1)dcosθi] ，n=1，2，...，N，符号 T 表示转置，j表示虚数，k为波数，Ns为噪声。

图1 均匀线阵布阵示意图Fig.1 Schematic diagram Uniform line array

根据常规波束形成理论，定义导向向量S=[s1s2...sN]T，其中，有K个互不相关的随机信号，则波束形成结果为

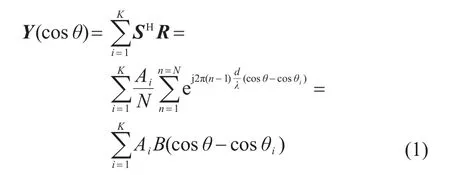
式中：H为共轭转置(具体推导参见文献[9])。由式(1)可以看出，B关于cosθ具有移不变性，即B(cosθ-cosθi)=B(cosθ|cosθi)，|B(cosθ|cosθi)|即为均匀线列阵在θi角度的指向性函数[11]。可将式(1)改写成积分形式：

1.2 反卷积波束形成

由式(1)、(3)可以看出，Bp是一个只与阵元个数、阵元间距和信号波长有关的函数(即均匀线列阵的PSF函数)，即在阵型确定的情况下，是可以提前确定的[12]；S是包含了目标方位信息的δ函数的和，这方位信息即所要求解的目标信息[13]；P作为CBF输出的功率谱，可以由阵接收到的数据获得。因此，由Bp、S和P三者之间的卷积关系可以推出，对P求反卷积即可获得目标的方位信息[13]。

目前，有多种算法可以进行反卷积，比如CLEAN[14]，反卷积波束形成法(Deconvolution Approach for the Mapping of Acoustic Sources Method,DAMAS)[15]，非负最小二乘法(Non-Negative Least squares,NNLS)[16]， Richardson-Lucy(R-L)迭 代 算法[17-18]以及相应的衍生算法[19]。由文献[16]可知，对于均匀线列阵这种PSF具有移不变特性的阵列，RL法相比于DAMAS、NNLS等算法具有更低的计算量，更易于工程应用。

R-L算法是一个基于贝叶斯准则的最优化迭代计算过程，将CBF功率谱结果作为初始值，每次迭代得到的功率谱估计值和CBF功率谱结果差值越小，则认为迭代得到的目标函数越接近真实的声源分布，取得极小值后即可停止迭代。也可直接指定迭代次数，在完成指定次数迭代后停止迭代[20]。具体的迭代公式为

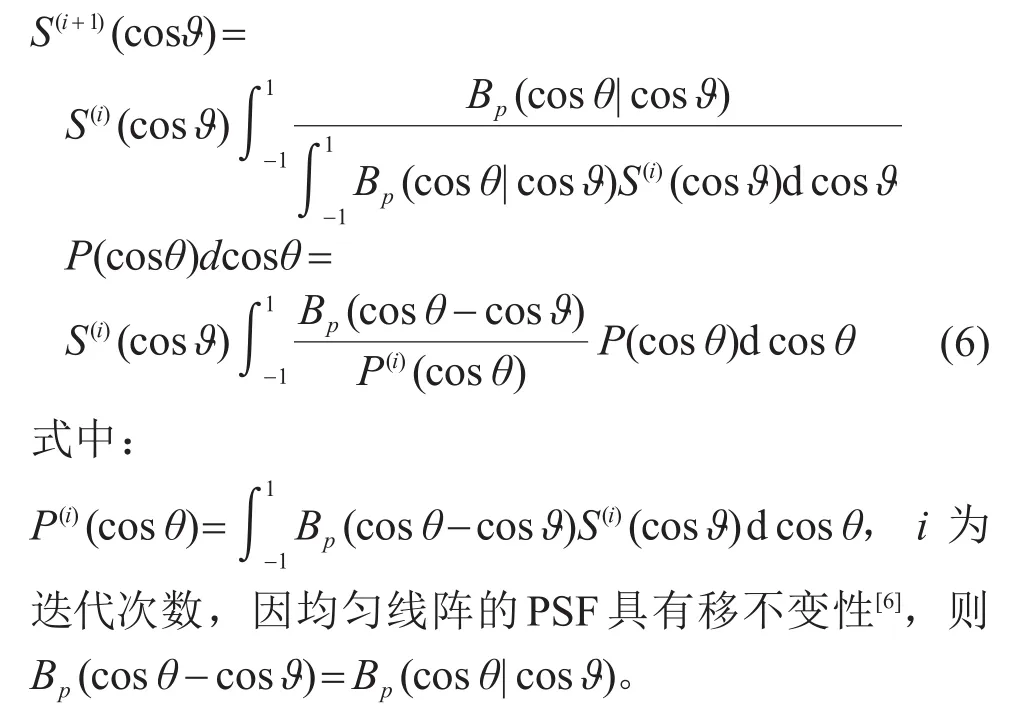
1.3 宽带随机信号处理

在实际的工程应用中，待分析的信号多为宽带随机信号，而由式(4)可知，反卷积算法中用到的PSF是一个与信号频率相关的参数，即：

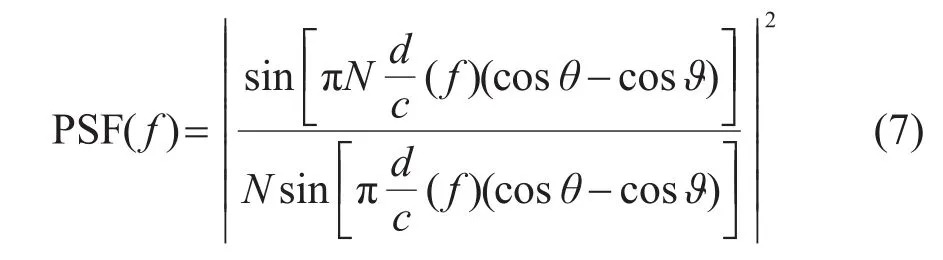
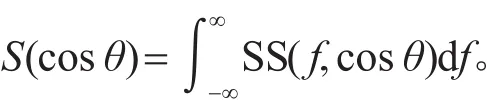
分析式(7)可知，PSF在一个较窄的频带内区别不大，而且频率越高，具有近似PSF的频带越宽。如图2所示。将宽带信号划分成若干个不等宽的较窄频带，每个频带内取一个频点的PSF做近似反卷积计算，这样可以极大地降低PSF和反卷积的计算量。

图2 各频率的点扩散函数Fig.2 PSF at each frequency

1.4 边界模糊问题的解决

人们在用R-L算法对二维图像进行反卷积处理时发现[9]，因为图像数据截止问题，恢复图像边缘部分会出现模糊。同理，对一维的CBF功率谱进行R-L迭代，也会在功率谱边界位置出现模糊现象，对于本文中的均匀线列阵来说，出现在cosθ=±1附近。文献[9]利用波束指向性图的周期性，给出了一种将功率谱积分范围扩展的方法，即将式(3)改写为

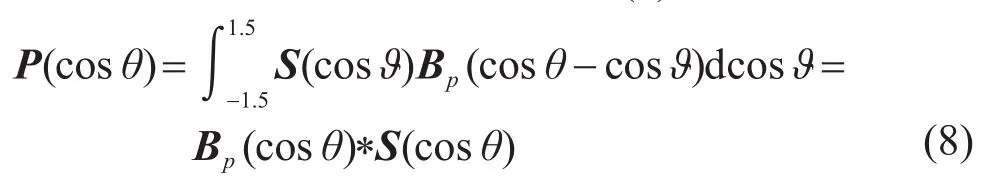
这样就将边界问题移动到cosθ=±1.5附近，在1＜|cosθ|≤1.5范围内会得到一个复数角度，仅参与计算，在具有实际物理意义的|cosθ|≤1范围内不受边界模糊影响。但是，这种边界扩展的方式在解决了R-L算法边界模糊问题的同时，增加了波束形成50%的计算量，尤其当波束个数较多时，这种计算量的增加极大地限制了算法在工程上的应用。

考虑到|cosθ|＞1范围内的波束形成结果，获得的θ值没有实际物理意义，在此花费较多时间计算有些得不偿失，为此，本文提出一种近似的优化方法，在不增加波束形成计算量的前提下，解决反卷积R-L算法带来的边界模糊问题。该方法具体步骤如下：

(1)按式(3)进行M个波束的常规波束形成计算，获得CBF的功率谱PM；

(2)以PM的左右端点为起点向两边各扩展M/4个波束，扩展波束以PM左右端点值为基准取值，获得扩展后的功率谱PkM，k=1.5；

(3)按-1.5≤cosθ≤1.5计算kM个波束的PSF函数；

(4)由PkM和PSF函数做R-L反卷积计算，取中间M个波束作为反卷积波束形成的输出结果。

2 仿真分析

通过计算仿真分析，首先验证了反卷积波束形成高分辨力和提高处理增益的能力。以64元的均匀线列阵为例，按信号频率为6 kHz进行半波长布阵，6 kHz窄带信号在不同信噪比和角度的仿真结果如图3所示。

图3中横轴为以cosθ值表示的角度，纵轴为以dB为单位表示的归一化后波束能量值。图3(a)为-90°方向的单目标，信噪比(Signal to Noise Ratio,SNR)为50 dB，图3(c)为图3(a)中虚线框局部放大，可以清楚地看出，在这种“理想”条件下，反卷积波束形成3 dB主瓣宽度约是CBF主瓣宽度的1/5。图3(b)为31°和33°方位的等强度双目标，SNR为-10 dB，3(d)为其虚线框局部放大，可以看出在这种仿真条件下，CBF已无目标分辨能力，而反卷积波束形成依然可以清楚分辨双目标。对比图中噪声部分，反卷积波束形成噪声能量比CBF低了约10 dB。

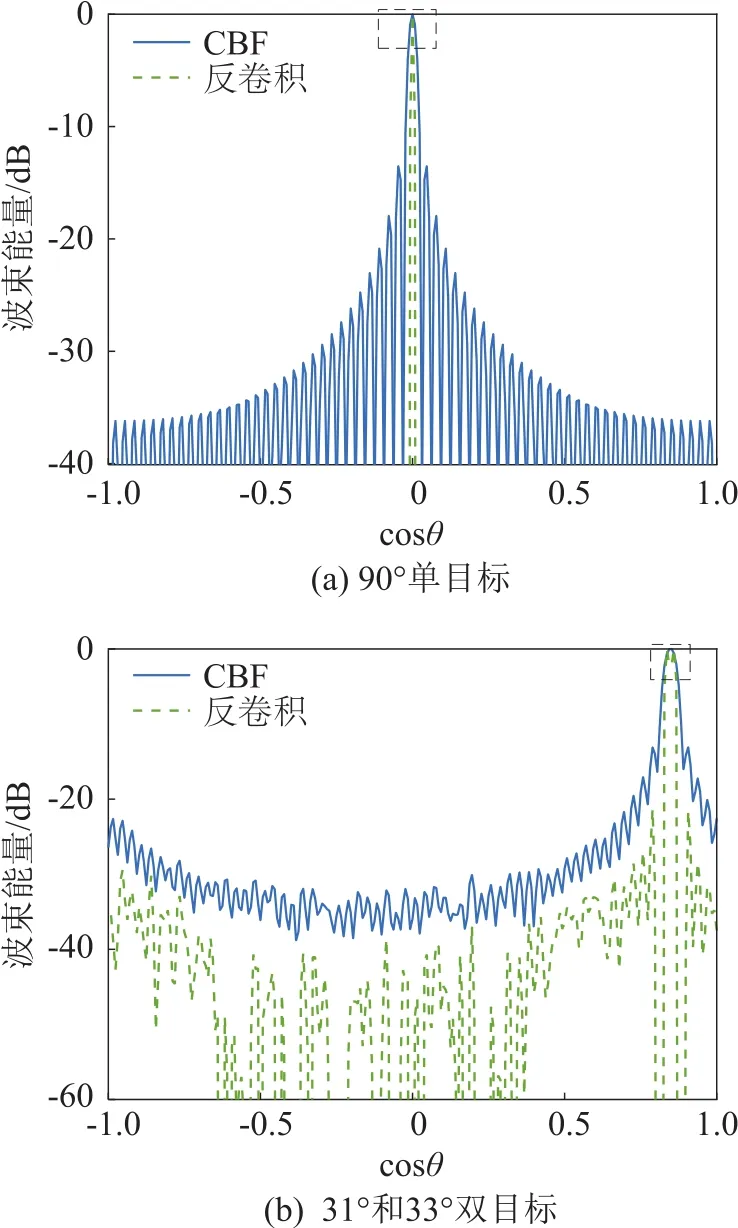
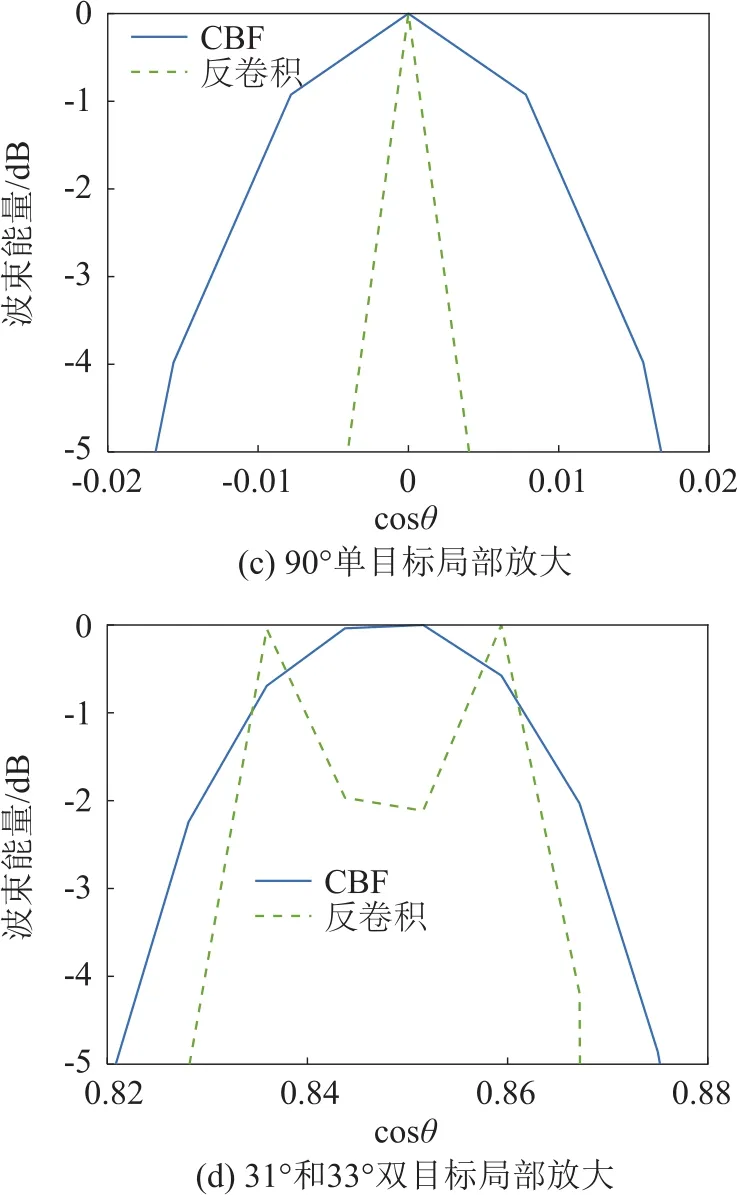
图3 窄带信号反卷积结果Fig.3 Deconvolution results of narrowband signal

以上仿真的单频窄带信号在实际工程应用中比较少见，对于常见的宽带信号，可以看作是多个窄带信号的叠加。以64元、6 kHz半波长布阵的均匀直线阵为例，工作带宽B=6 kHz，由图2可知，各频点PSF不同，即按传统的反卷积波束形成算法，需要对带宽内的所有频点都做反卷积运算，这无疑增加了很多计算量。为了减少不同频点的反卷积运算，利于工程应用，本文提出将宽带拆分的方法，将整个工作带宽B拆分成(0～200 Hz)、(200～500 Hz)、 (500～1 000 Hz)、 (1000～3 000 Hz)和(3 000～6 000 Hz)共5个相对较窄的频带，并取每个频带中心频点的PSF做反卷积波束形成。因各频带仿真结果具有相似性，本文仅给出1 000～3 000 Hz频带随机信号的仿真结果。

图4中横轴为以cosθ值表示的角度，纵轴为以dB为单位表示的归一化后波束能量值。图4(a)中信号SNR为0 dB，图4(b)中信号SNR为-20 dB。对比两图可以看出，因为利用了不同频点的PSF信息，全频点反卷积在性能上优于窄带中心频点反卷积，但在信号SNR较低时，两种方法检测能力和分辨力近似，都优于CBF。对弱目标检测而言，窄带中心频点反卷积具有计算量更小的优势。

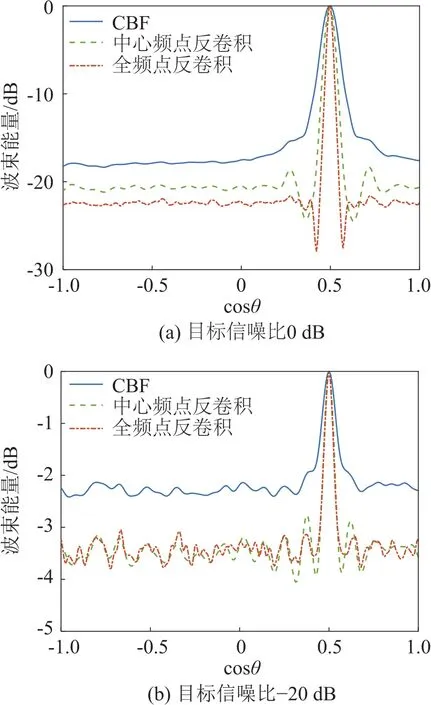
图4 全频点和窄带中心频点反卷积结果Fig.4 Deconvolution results at total frequency points and at the central frequency point of each narrow band

对于R-L迭代算法的边界模糊问题，以64元6 kHz半波长布阵的均匀直线阵进行仿真，SNR为0 dB，目标来波方向分别为90°和10°，仿真结果如图5(a)、5(b)所示。

图5 中横轴为以cosθ表示的角度，纵轴为归一化后波束能量值。图5(c)为图5(a)中虚线框局部放大。图5(d)为图5(d)中虚线框局部放大，由图5可以看出，未作周期扩展的反卷积结果在cosθ=±1附近会出现波形畸变，这会给检测带来虚假目标；当目标出现在边界位置时，会造成目标方位估计误差。与之相对的，进行了周期扩展的反卷积相比于CBF提高了检测能力和分辨力，并且结果准确。

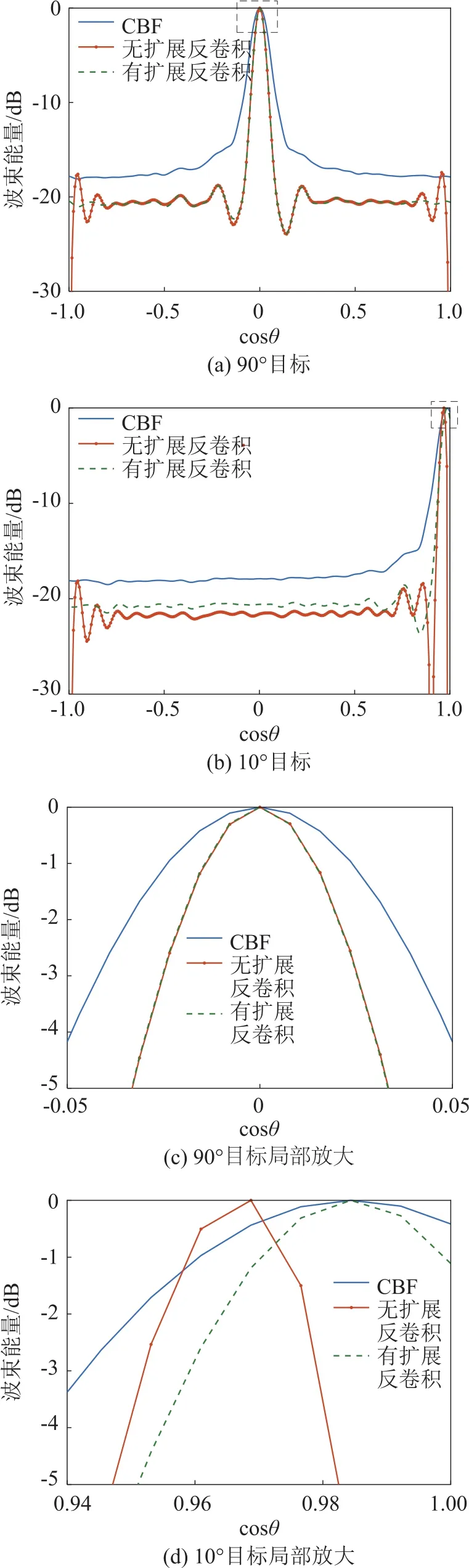
图5 R-L迭代算法的边界模糊问题验证Fig.5 Validation of boundary blur problem of R-L iterative algorithm

由以上仿真可知，利用R-L迭代算法的反卷积波束形成需要进行周期扩展。但是，对波束进行扩展会极大地增加CBF的计算量，为此本文提出一种优化方法，并进行如下仿真：64元6 kHz半波长布阵的均匀直线阵，(1 000～3 000 Hz)宽带随机信号，对CBF的能量谱做边界扩展和反卷积，与对波束进行扩展的反卷积结果进行对比，结果如图6所示。

图6(a)中目标在60°，SNR为0 dB可以看出在较高信噪比条件下，两种反卷积方法检测能力一致，都优于CBF；改变信号SNR为-20 dB，仿真结果如图6(b)所示，对比图6(a)、6(b)可以看出，在不同的SNR条件下，当目标不在边界位置，两种反卷积方法对目标检测能力和分辨力一致，在边界处的噪声有一点差别，但对目标检测来说，基本没有影响；图6(c)为目标在10°，SNR为0 dB的仿真结果，图中虚线框局部放大如图6(e)所示。因为目标在边界位置，对CBF能量谱进行边界扩展时会将目标信号的能量扩展，在做反卷积时，这部分扩展的信号能量会泄露到噪声中，增加了噪声的谱级。对波束扩展，相当于增加了虚拟的角度范围，对cosθ=±1附近的目标不会有影响；改变图6(c)中的信号SNR为-20 dB，仿真结果如图6(d)所示，图中虚线框局部放大如图6(f)所示，与图6(c)、6(e)对比可知，在较低的SNR条件下，目标分辨能力有所降低。由图6(a)～6(e)可知，对波束扩展的反卷积算法不受目标位置影响，能一直保持较好的检测能力和分辨力。对CBF能量谱扩展的反卷积算法的性能会受目标位置影响，当目标不在边界位置时，其具有与波束形成时周期扩展的反卷积算法一样的检测能力和分辨力；当目标在边界位置时，算法性能会有一定下降，但依然优于CBF。另外，考虑实际应用情况，均匀直线阵在cosθ=±1位置附近为检测“盲区”，一般不作为基阵的主要观测方向，以降低“盲区”的部分检测性能换取计算量的大幅下降，CBF能量谱边界扩展的反卷积算法在工程应用上依然有其优势。

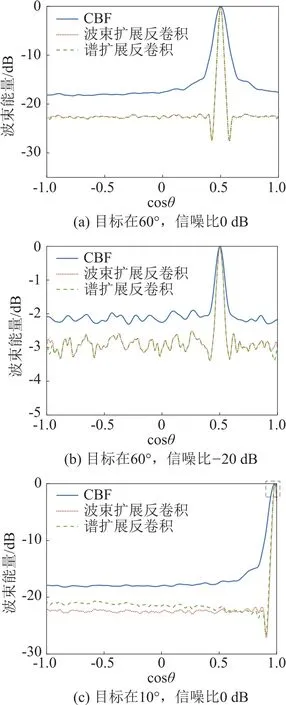
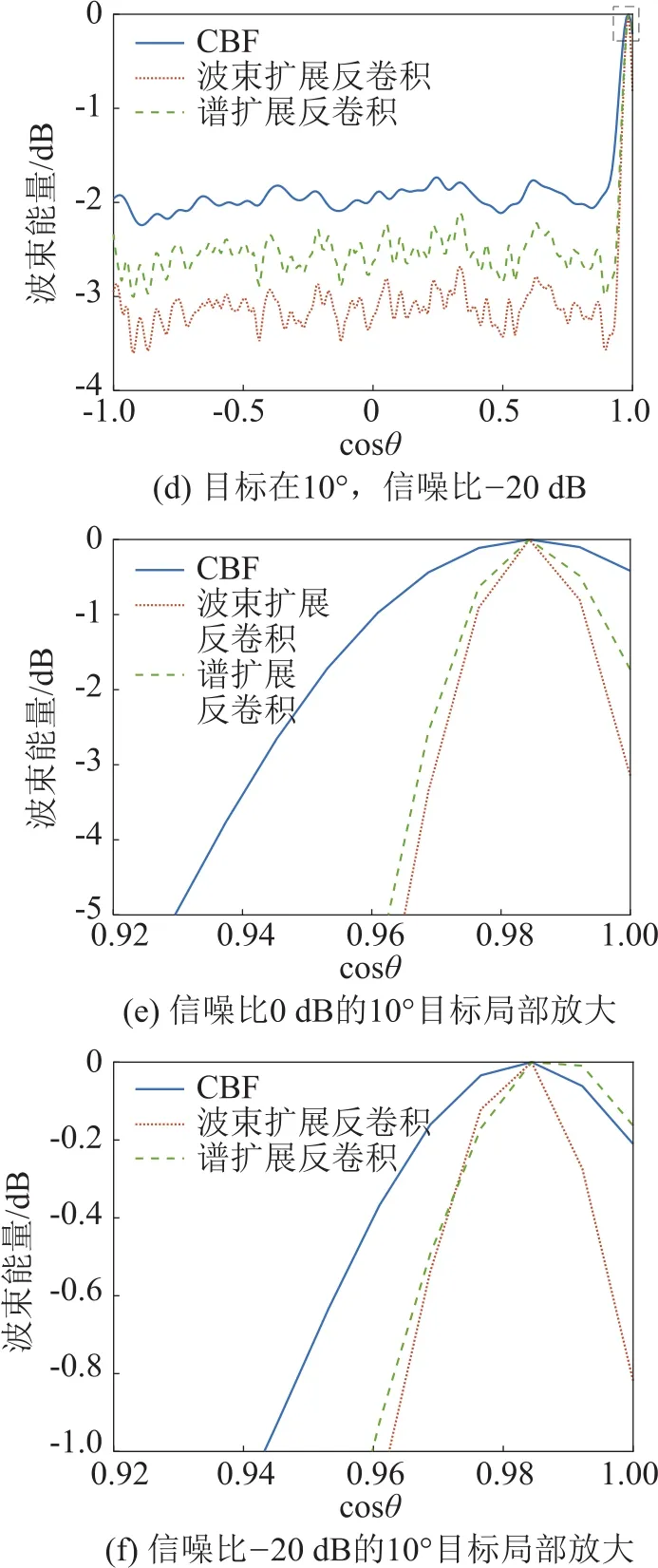
图6 波束扩展反卷积和谱扩展反卷积的处理结果对比Fig.6 Comparison of processing results between beam expansion deconvolution and spectrum expansion deconvolution

综合以上两种计算速度的提升方法，对一宽带随机信号，做129个波束全频点的CBF，周期扩展为193个波束，每12个快拍进行一次能量积分，共1 200个快拍数据，反卷积迭代10次，对本文所提的快速方法与传统反卷积波束形成算法进行了计算速度的对比，记录仿真总时间(PSF计算采用预存方式，不计入总时间)，结果如表1所示(因仿真平台性能差异，此计算时间仅作对比参考)。

由表1中的第2行可以看出，在单频点情况下，两种方法反卷积计算时间一样，计算速度差距主要体现在波束个数上，因传统方法要在波束域做1.5倍扩展，整体计算时间也是本文方法的约1.5倍。传统方法反卷积迭代所耗时间与分析频点个数成正比，本文方法反卷积迭代所耗时间与拆分窄带个数成正比，随着分析带宽的增加，频点个数会远大于拆分窄带个数，传统方法所耗时间的增加也会远大于本文方法所增加的时间。表1所示仿真结果与理论分析一致，即相比于传统方法，本文方法整体计算速度在单频点时提升了约50%。这也是本文方法速度提升的下限，随着分析频点的增多，本文方法的速度提升也随之增大。

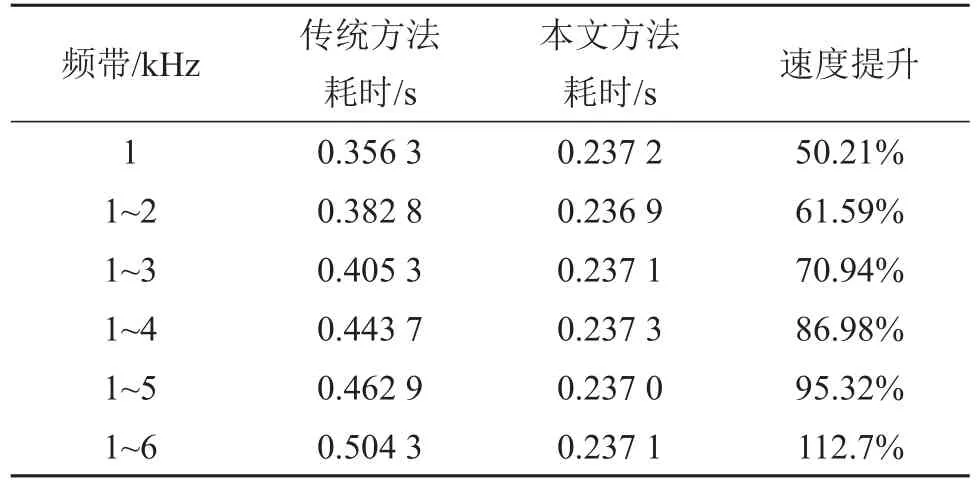
表1 传统的和本文提出的反卷积波束形成方法的计算速度对比Table.1 Speed comparison between conventional and the proposed deconvolution beamforming methods

3 试验验证

选取一段海上试验数据对本方法进行了验证，试验时两艘船在一均匀直线阵正横方向交叉航行，按本文方法将分析带宽划分成多个较窄频带，分别进行CBF和反卷积处理，选取低频和高频两个频段进行对比分析，具体结果如图7所示。

图7中横轴为方位，以cosθ值显示；纵轴为实验的时间批次，1为最早时刻。对比图7(a)、7(b)，可以直观地看出，本文快速反卷积算法处理后的主瓣波束宽度要明显小于CBF，图7(a)中两目标交叉无法分辨时间约380批次，而图7(b)中仅约240批次。从图7(b)中可以看出，在cosθ(0.6～0.75)范围内有一较弱目标，而在图7(a)的相同位置，此目标并不明显，大部分“淹没”在噪声中，由此可以看出，本文中的快速反卷积算法对弱目标的检测能力有了一定提升。图7(c)、7(d)中的高频处理结果，相比于低频，高频时主瓣波束宽度都有明显降低，在图7(c)中两目标交叉无法分辨时间约190批次，在图7(d)中约130批次。图7(c)中两个目标左侧都存在较高的旁瓣，与之相比，图7(d)中的旁瓣被削弱。

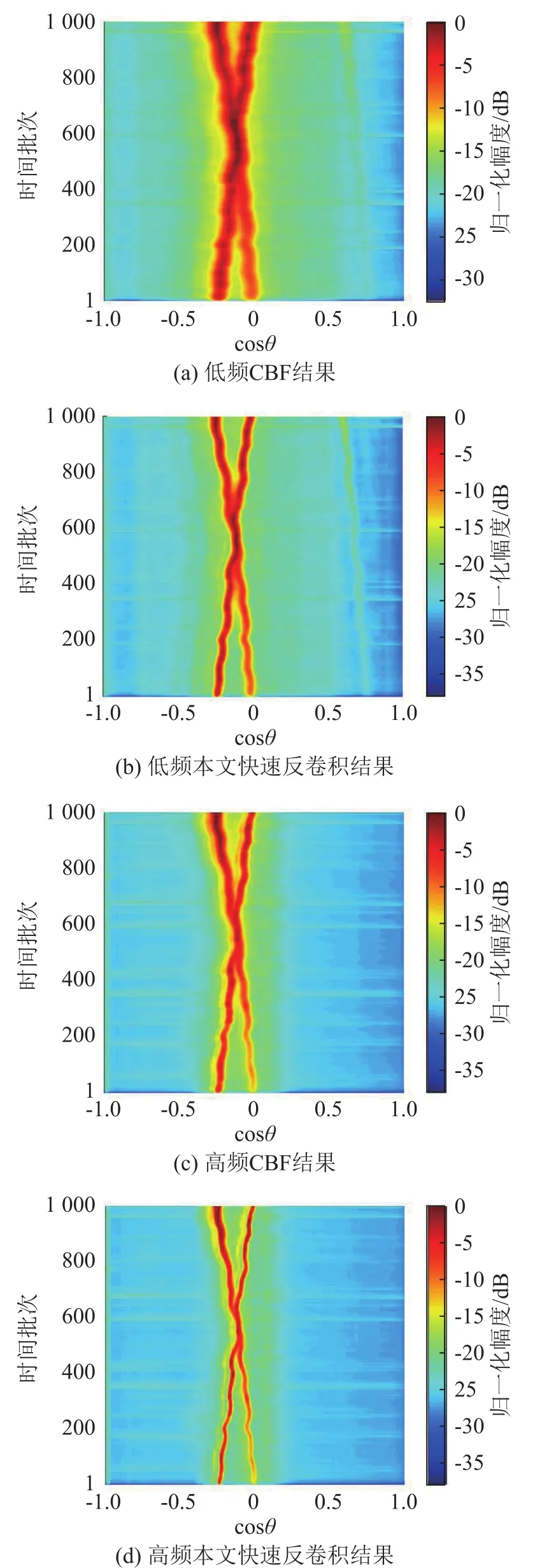
图7 两种方法对实际海试数据的处理结果Fig.7 Processing results of real sea trial data by the two methods

4 结论

相比于CBF方法，反卷积波束形成方法具有更高的分辨力、更高的处理增益和更好的旁瓣抑制能力，但作为CBF的一种后置处理方法，计算量有所增加。对于宽带随机信号的处理，因为利用了不同频率的PSF，全频点反卷积在高SNR条件下性能优于本文提出的窄带中心频点反卷积方法；但在低SNR条件下，两者检测性能相近，而中心频点反卷积方法因其计算量远小于全频点反卷积方法，在工程应用上更具有优势。对于R-L算法的边界模糊问题，本文提出了一种在CBF能量谱上进行边界扩展的方法，相比于在波束角度上进行扩展，既解决了R-L算法的边界模糊问题，又极大地降低了波束形成的计算量，更利于工程实现。综合两种速度提升方法后，本文方法相比于传统反卷积波束形成速度至少提高了50%。

海试数据的处理结果也验证了本方法的有效性。结果显示，本方法具有更高的分辨力，提高了对弱目标的检测能力，对旁瓣级的抑制在5 dB以上。