微纳卫星空间外热流仿真分析

李雅琪

（华北水利水电大学 信息工程学院，河南 郑州 450046）

0 引 言

微纳卫星拥有体积小、重量轻、耗电量少、研发周期短、性价比高等众多优点，近年来，在通信、遥感、导航等方面都得到了迅速的发展，拥有良好的应用前景。绕地微纳卫星在轨运行期间，除了真空、微重力的环境影响外，空间外热流对卫星热环境变化起着直接性的作用。周期性变化的空间外热流使卫星温度场随时间变化，给卫星结构的稳定性和热控措施的选择带来了巨大挑战。因此，对空间外热流进行分析是卫星热分析不可或缺的前提。

很多研究者已经研究了空间外热流的计算流程和建模方法。柏添等利用热仿真软件计算了夏至日和冬至日两个工况下的外热流，为卫星的热设计提供了参考。李志松等综合考虑了卫星的姿态角信息，计算了六面体卫星各个面上所受的外热流的值，并突破了卫星进入阴影期和热平衡方程对真近点角连续积分的技术问题。李运泽等构建了卫星本体质心坐标系，利用太阳向量和地球向量来描述卫星相对地球和太阳的轨道运动，简化了卫星各个面空间外热流的计算。王晓明等将卫星本体简化为球体，分析了星外设备与本体遮挡时，星外部件和卫星本体所受的外热流变化。易桦等分别采用解析法和数值积分法计算太阳辐照热流，和地球红外辐照热流、地球反照热流，极大的简化了计算过程。

本文将综合考虑在轨运动过程中卫星的轨道位置情况，对卫星所受的空间外热流进行建模仿真。在外热流的计算中，选用本体质心坐标系，快速计算了六面体卫星各个面所受的空间外热流，对仿真结果进行了详细的分析讨论，模型具有良好的通用性。

1 理论分析与建模

卫星在轨运行中所受的空间外热流与它和地球、太阳之间的位置直接相关。卫星在轨道平面内，轨道平面围绕地球不断运动，地球作为太阳的行星，绕太阳不断运动，使得卫星、地球、太阳三者之间的相对位置随时间不断变化，空间外热流也随之不断变化。确定卫星的空间外热流分布，首先要确定卫星的轨道运动情况。

1.1 轨道计算

选用李运泽教授提出的本体质心坐标系进行模型的构建：O为卫星质心，x轴指向轨道运动方向，y轴垂直向下，z轴始终指向地心。

卫星在地球轨道上的位置与当前时刻、真近点角和星地距离有关。

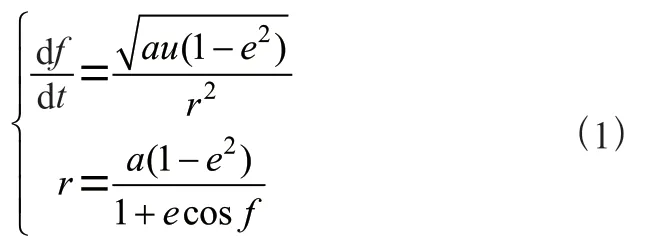
其中，为卫星轨道半长轴，为地心引力常数，为轨道偏心率。在设定的初始值及其在时刻的导数值后，可以使用龙格-库塔法求解上述非线性微分方程。

轨道周期是指卫星环绕地球一周所需要的时间，卫星在一个轨道周期的时长可用下式计算：

其中，为开普勒常数。

卫星进入阴影区时，失去了主要的热量来源——太阳光，将不再受到太阳辐照和地球反照的影响，所受的热量在短时间内会急剧减小；出阴影区时，所受的热量会急剧增加，若无法保证卫星在此刻维持热平衡状态，卫星的剩余寿命将会大大缩短。卫星进入阴影区的临近点为：

其中：R为地球半径，i为太阳光线与轨道面的夹角。当≥时，卫星进入阴影区，反之，当＜时，卫星进入光照区。

1.2 外热流计算

在太空中，大部分的空间都是空荡的，各类天体所占的体积较小，由于空间辐射能力有限，卫星在太空中的环境可以看作黑体辐射环境。绕地卫星处于中、低轨道时，只考虑太阳辐照热流、地球红外辐照热流、地球反照热流带来的影响。准确的计算在轨道周期内空间外热流的瞬时值并探究其变化规律，可以为卫星的热分析提供可靠的初始条件和热边界条件。

1.2.1 太阳辐照热流

太阳辐照热流是卫星表面最主要的热量来源，在一年之内变化最大。在近地轨道和地球静止轨道的高度上，太阳光被认为是均匀的平行光束，当卫星处于光照区时，卫星表面任一微元表面上所受到的太阳辐照热流为：

其中，为单位面积太阳辐照强度，β为卫星外表面微元表面的法线与太阳光线之间的夹角。单位面积太阳辐照强度由式（5）计算。

其中，e为地球绕太阳运行的轨道偏心率，φ为太阳位置，用黄经描述，a太阳与地球之间的平均距离，C为太阳常数。太阳辐照强度在一年之内随太阳黄经有规律的发生变化，范围在1 320～1 420 W/m，在夏至日达到最小值，在冬至日达到最大值。

当卫星处于阴影期区时，卫星外表面将不会直接受到的太阳辐照热流的影响。

1.2.2 地球红外辐照热流

地球表面以红外波长辐射所有的能量，由于地球的温度随时间和地理位置而异，卫星所受到地球红外辐照热流强度也会随时间和其在轨道上所处的位置而变化。因此，对于卫星表面F所受地球红外辐照的计算，如下式计算：

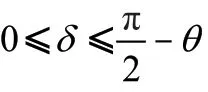
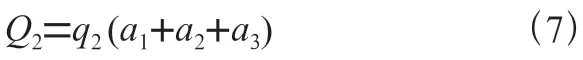
其中，为F表面的法线与地心连线的夹角，为经过F表面的地球切线与地心连线的夹角，由式（8）计算；是单位面积的地球红外辐照强度，由式（9）计算，为对太阳光的反照比，通常取0.3。、和的计算方法由式（10）所示：

其中，R是地球平均半径，是卫星距地心的距离。

1.2.3 地球反照热流

地球反照包括被大气层的分子、微尘等散射的太阳辐射和到达地球表面被地球表面反射的太阳辐射两部分，其数值与地球表面的大气特性和地理经纬度有关。从辐射的类型来看，要比太阳辐照和地球红外辐照的计算复杂。为了方便计算，结合地球红外辐照结果计算地球反照热流。

为单位面积地球反照强度。为卫星、地球和太阳三者之间的夹角。

2 仿真结果及分析

2.1 空间外热流仿真

以某近地轨道六面体微纳卫星为例，选用Java语言编程，运用上述模型进行仿真。卫星的外形、轨道参数和飞行姿态一起决定了卫星各面受空间外热流值的大小，该卫星相关仿真参数如表1所示。该微纳卫星在轨飞行中保持三轴稳定，则仅考虑轨道位置对卫星各表面所受外热流的影响，暂不考虑卫星姿态变化带来的影响。利用公式可求得轨道周期为5 808 s，设置仿真时长为1个周期，仿真日期为春分日，初始位置在近地点，进行在轨卫星的空间外热流仿真，在仿真周期内阴影期为959 s～3 050 s，其余时间卫星处在光照区。

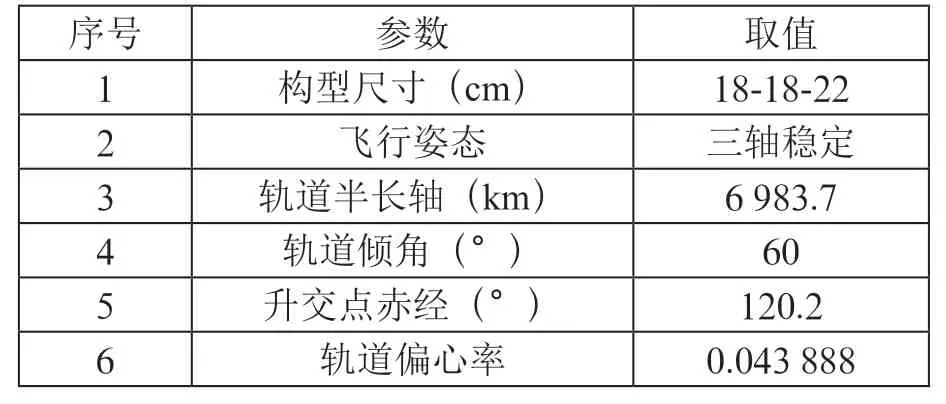
表1 基本参数表

由图1、图2不难看出，卫星所受空间外热流呈周期性变化。在光照区时，太阳辐照热流占比最大，依次是地球红外辐照热流和地球反照热流。在进入阴影期的瞬间，由于失去了太阳光的照射，太阳辐照热流迅速下降。同时，地球反照大部分为到达地球表面而被地球表面反射的太阳辐射，由于卫星-太阳-地球三者之间的相对位置关系，在卫星进入阴影区之前的一段时间内，地球反射的太阳光就无法直接抵达卫星表面，在这段时间内卫星只受地球红外辐照热流的影响。在阴影区内，卫星也只受到地球红外辐照热流的影响。

图1 卫星所受空间外热流

图2 卫星六个面所受太阳辐照热流

在春分日时，卫星的Y2面平行于轨道平面。在光照区，Y2面与太阳光线之间的夹角不变，受到的太阳辐照热流的值是恒定的，而Y1面由于受不到太阳光的照射，所以接收到的太阳辐照值为0。卫星的其他表面在仿真周期内与太阳光的夹角实时变化，所以接收到的太阳辐照热流也是变化的。

2.2 夏至日和冬至日对比

分析该微纳卫星各表面在一年内接受外热流的变化情况，可以得到，太阳辐照在卫星所受的外热流中占比最大，且太阳辐射强度在一年之内变化也最大，在冬至日达到最大值，在夏至日达到最小值。为进行对比，选择夏至日和冬至日卫星各个面所受总外热流进行对比分析，仿真结果如图3所示。

图3 夏至日和冬至日卫星所受空间外热流

计算出的空间外热流结果与参考文献[7]的变化趋势一致，在最大值处略有不同，是由于单位面积辐照强度和面积不同引起的。夏至日时，Y2面在一个周期内都受不到太阳光的照射，其总外热流由于太阳辐照热流的缺失，总外热流较低。在冬至日时，Y1面则无法接受到太阳光的照射。由各个面冬至日和夏至日所受外热流数值上的对比可验证夏至日卫星所受外热流较冬至日低，卫星所受总外热流在冬至日达到最大值，在夏至日达到最小值。

3 结 论

本文针对空间外热流进行仿真分析，得出以下3点结论：

（1）本文分析了卫星、太阳和地球三者之间的空间几何关系，计算了相关卫星轨道参数和轨道运动周期，并判断了卫星进入阴影区的关键点。

（2）根据空间几何关系推导了卫星在轨运动周期内瞬时所受空间外热流的计算公式，建立了空间外热流计算模型，对仿真结果进行了详细的分析和讨论，验证了卫星所受空间外热流的规律。

（3）同时验证了冬至日和夏至日空间外热流分别达到最大值和最小值。