落岩撞击作用下连续刚构桥车-桥耦合振动研究

秦文涛,郭小坤,郭军峰,郝 璐,洪碧武

(西南交通建设集团股份有限公司,云南 昆明 650000)

随着我国交通运输事业的蓬勃发展,中国桥梁建设取得了宏伟成就,高墩大跨桥得到了广泛的应用。车辆通过桥梁时会使桥梁产生振动,桥梁振动又反过来影响车辆振动,车辆与桥梁之间的相互作用称为车-桥耦合振动。近年来,随着我国汽车运输密度、载重和行车速度不断提高,车辆与高墩大跨桥间的耦合振动越发复杂和不确定。过重和过快的车辆将加剧对桥梁的冲击,影响桥梁结构安全,而桥梁过大的振动也反过来影响车辆行车舒适性和安全性。众多学者从理论推导和工程应用两方面对车-桥耦合振动展开了丰富的研究工作。邓露等[1]总结了车-桥系统振动的研究进展,概括了车-桥耦合振动的理论研究和工程应用；陈水生等[2]推导出车辆各轮相干桥面不平顺激励法,并验证了所提方法的可靠性;Wang等[3]研究了强风作用下车-桥动力响应,探讨了风荷载对车-桥系统的影响。也有一些学者研究了不同桥梁结构在不同影响因素下的车-桥耦合振动,得出不同桥型的车-桥耦合振动差异较大的结论[4-6]。

落岩撞击是我国西部山区桥梁经常面临的自然灾害,对桥梁结构安全影响较大。落岩撞击桥梁会产生巨大的破坏力,使桥梁或桥墩产生结构损伤甚至破坏,这一直是工程师们研究的热点。Zhang等[7]研究了落岩撞击桥墩机理,探讨了落岩撞击速度、落岩直径等对桥梁的影响和对桥上车辆的影响；朱俊宇[8]研究了不同落岩撞击下桥面板的力学行为,探讨了动力响应放大系数的变化规律。

我国西部山区修建有大量的高墩大跨连续刚构桥,由于薄壁空心墩高度大且柔性低,车-桥振动尤为突出。目前关于高墩大跨连续刚构桥车-桥耦合振动研究较少[9],而落岩撞击作用对高墩大跨连续刚构桥车-桥系统的影响更是少有提及。基于此,结合已有研究成果,建立了考虑落岩冲击影响的车-桥动力学模型,采用非一致桥面不平顺激励法,探讨了落岩冲击桥墩对大跨度连续刚构桥车-桥耦合振动的影响,并进一步分析了落岩冲击对桥上车辆行车舒适性的影响。

1 落岩撞击作用下车-桥耦合动力学模型

车-桥动力学模型由车辆子系统和桥梁子系统组成,车辆与桥梁之间通过车轮与桥面之间接触点的力与位移的关系相互耦合,车-桥动力学方程可表示为

(1)

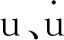
1.1 车辆动力学模型

采用文献[10]中提出的车辆模型,该模型符合中国公路车辆特点,车辆模型和车辆参数分别见图1和表1。

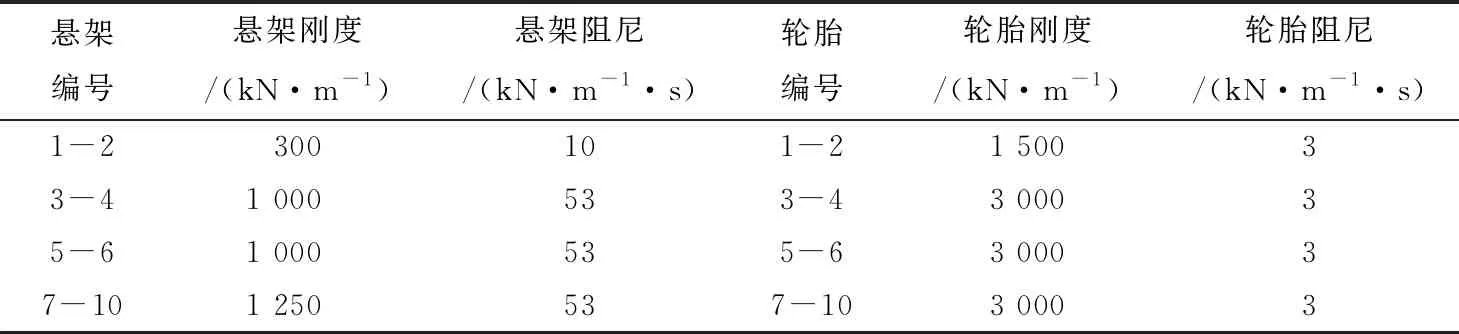
表1 车辆模型参数

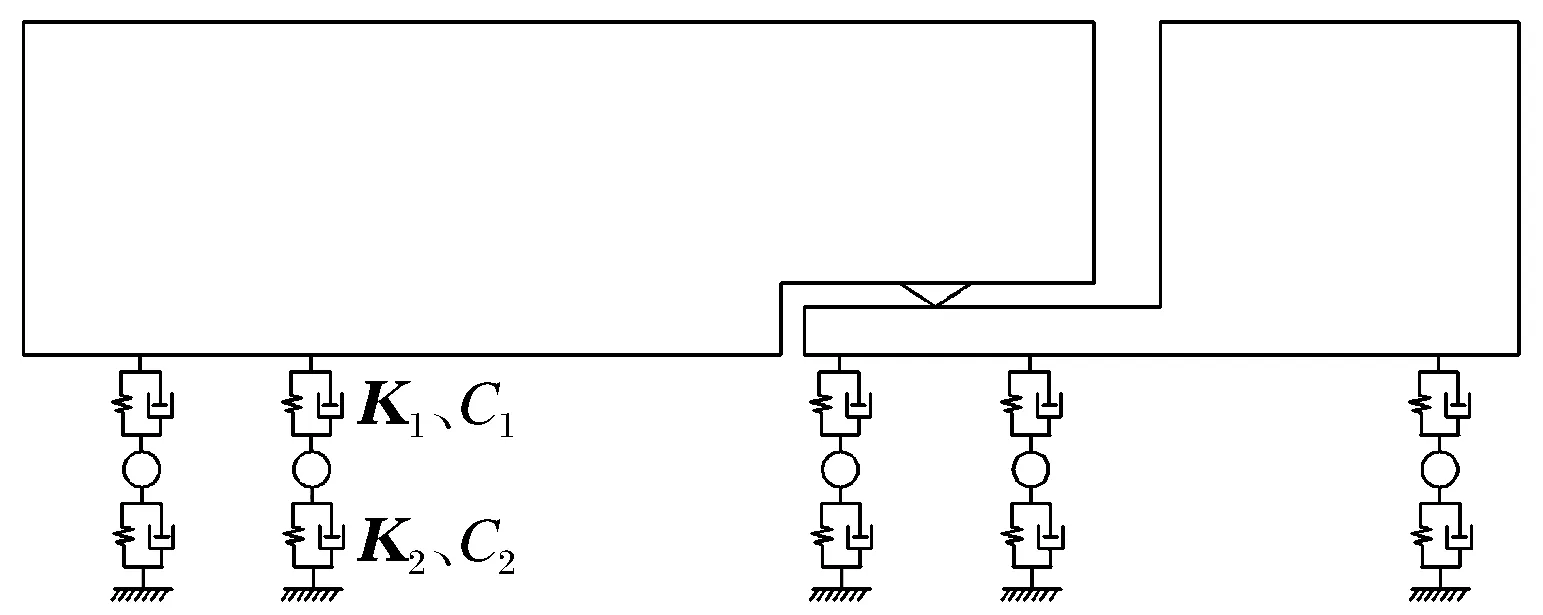
图1 车辆模型

1.2 桥梁动力学模型

采用ANSYS建立全3D桥梁模型,主梁和桥墩均采用实体单元,基础采用弹簧单元,采用Rayleigh阻尼,阻尼比取值2%。

1.3 桥面不平顺

采用功率谱密度函数来计算桥面不平顺,其中三角级数法和Fourier法比较常用。研究选取三角级数叠加法获得了桥面不平整度。由文献[11]可知,非一致桥面不平顺激励能更加准确的反映车-桥耦合振动,参考文献[11]中获得了左右轮非一致桥面不平顺,如图2所示。

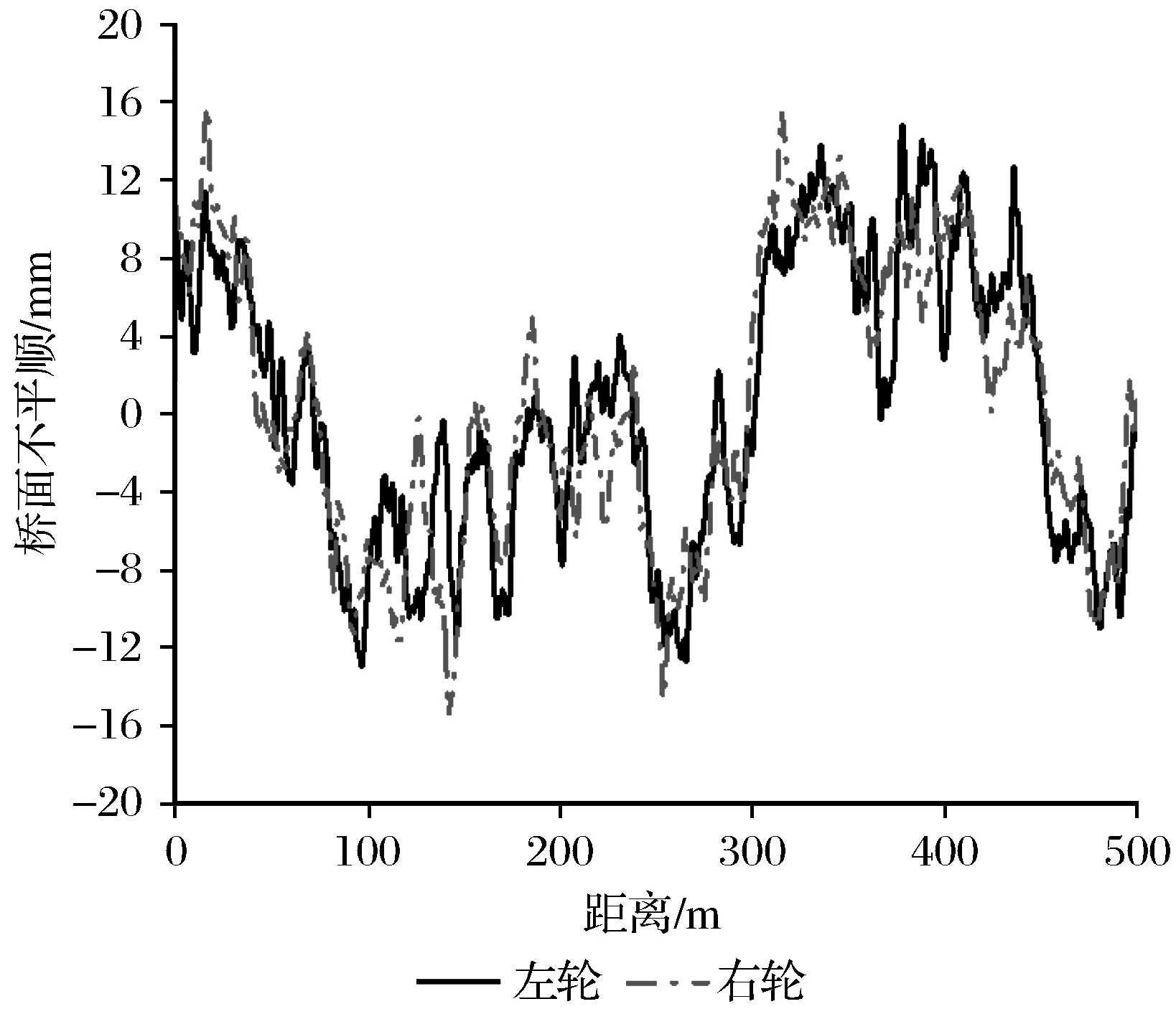
图2 桥面不平顺

1.4 落岩撞击荷载计算

落岩撞击荷载通常由两种方式得到:试验法和数值仿真法。研究采用LS-DYNA建立落岩-桥墩撞击有限元模型,桥梁结构为大跨度连续刚构桥,计算跨径为90 m+170 m+90 m,主梁采用C50混凝土,端部截面梁高10 m,跨中截面梁高3.7 m,桥墩为薄壁空心墩结构,采用C40混凝土,墩高50 m,桥梁截面如图3所示。

建模中将主梁和二期恒载作为附加质量施加在桥墩上,桥墩采用solid164单元模拟,单元尺寸为0.4 m×0.4 m×0.4 m。落岩采用直径为2 m的刚性球体模拟,材料属性见文献[12],落岩网格尺寸为0.2 m×0.2 m×0.2 m,撞击位置为距墩底25 m处。考虑到落岩与桥梁撞击部位的网格尺寸大小直接影响落岩撞击力的精度,桥墩撞击位置处网格尺寸为0.2 m×0.2 m×0.2 m。为了避免落岩与桥墩初始状态发生穿透现象,建模时桥墩与落岩的初始距离为5 m,撞击速度为10 m/s。模型计算过程中,接触类型采用双向接触算法中的面与面自动接触,接触算法为对称罚函数算法。落岩-桥墩撞击模型如图4所示,计算的落岩撞击荷载如图5所示。

2 落岩撞击作用下车-桥系统动力分析

2.1 研究对象

基于前述的车-桥耦合动力学模型,采用图3所示的大跨度连续刚构桥为研究对象,分析落岩撞击作用下车-桥系统耦合振动。当车辆行驶到第二跨跨中时,将计算得到的落岩撞击时程力以外荷载的形式加在2号桥墩上,桥梁有限元模型和车辆行驶位置如图6所示。

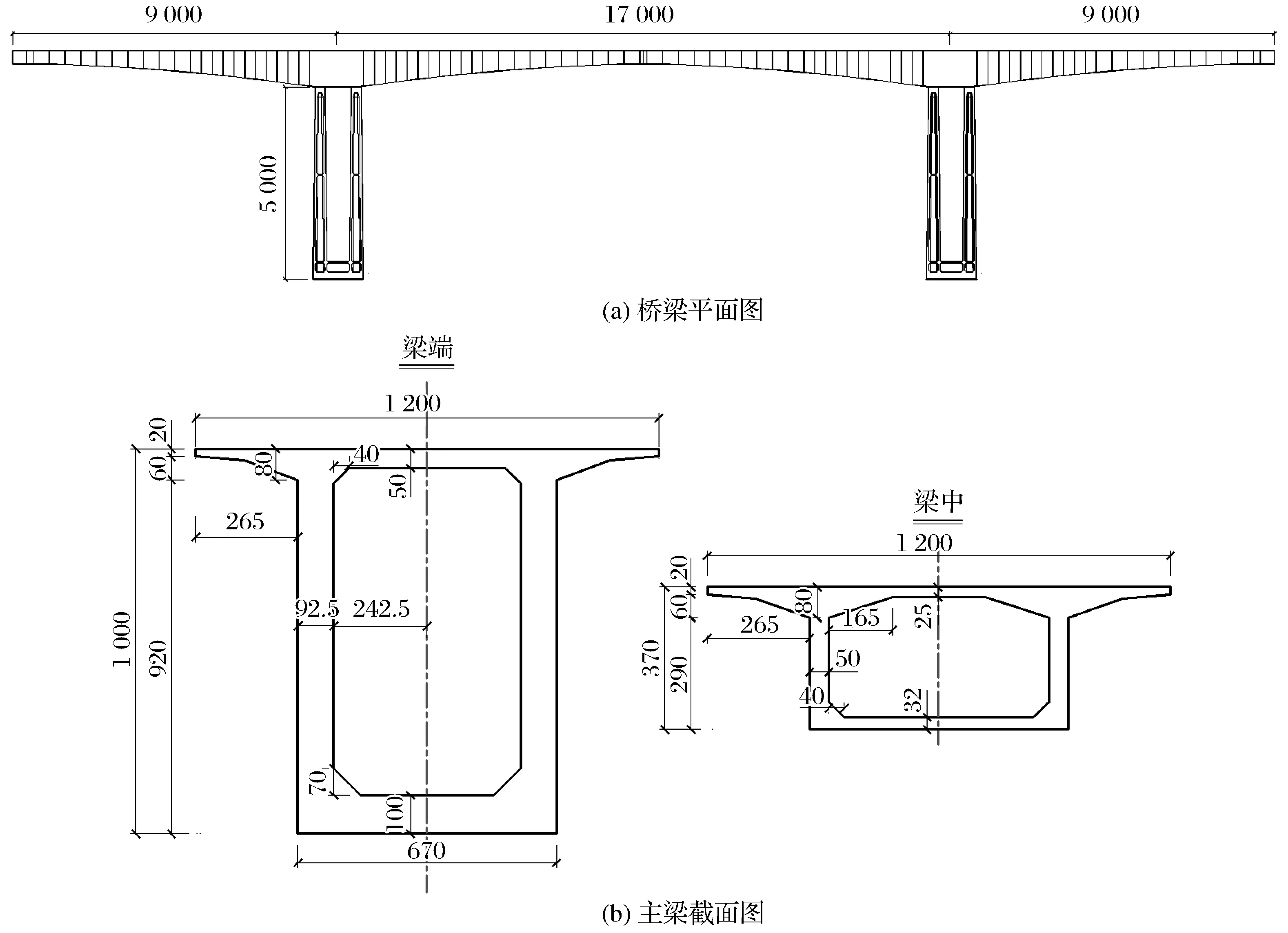
图3 连续刚构桥平面布置(单位:cm)

图4 落岩-桥墩撞击模型

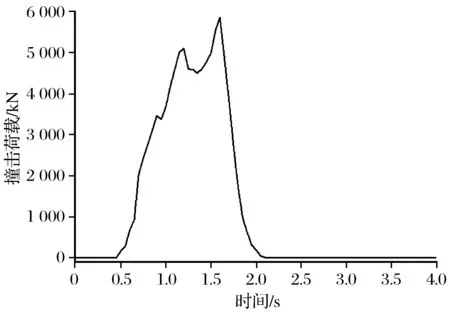
图5 落岩撞击荷载

图6 桥梁有限元模型和车辆加载位置

2.2 落岩撞击对车-桥系统的影响

控制行车速度为80 km/h,采用非一致桥面不平顺激励,分析了有落岩撞击和无落岩撞击两种工况下车-桥耦合振动。由于落岩撞击主要影响桥梁横向振动,此处主要分析车-桥耦合横向振动。桥梁第二跨跨中横向位移和加速度曲线如图7所示。

由图7可知,落岩撞击桥墩对大跨度连续刚构桥横向振动影响较大。在落岩撞击作用下,桥梁横向位移和横向加速度均急剧增大,其中横向位移和横向加速度峰值分别约为无落岩撞击工况的2.05倍和2.71倍。

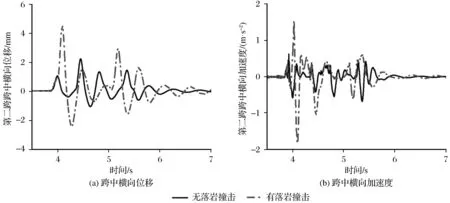
图7 两种工况下车致桥梁横向振动

2.3 行车速度对车-桥系统的影响

为了进一步分析落岩撞击桥墩对车-桥耦合振动的影响,控制桥面不平顺不变,改变行车速度为40 km/h、60 km/h、80 km/h、100 km/h,计算了落岩撞击作用下不同行车速度对桥梁横向动力学的影响,不同时速下桥梁横向位移和加速度如图8所示。

由图8可知,行车速度对落岩撞击作用下桥梁横向振动影响较大。随着行车速度的增加,桥梁跨中横向位移和横向加速度均增大,其中车速100 km/h时的桥梁横向位移和加速度峰值分别为车速40 km/h时的1.38倍和1.43倍。

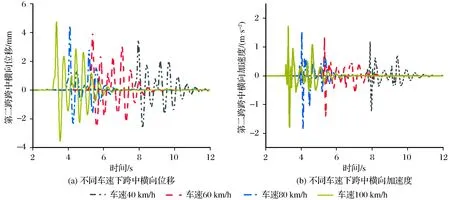
图8 不同车速下桥梁横向振动

3 落岩撞击桥墩对行车舒适性的影响

国际上行车舒适性评价指标主要有ISO2631和Sperling指标,其中Sperling指标依据车辆冲击动力和振动能量的乘积为标准来判断行车舒适性,其表达式为

(2)

其中:Z0为车辆振幅(cm);f为振动频率;a为加速度(cm/s2);F(f)为与振动频率有关的加权系数。

Sperling指标的取值范围如表2所列。

表2 Sperling指标

3.1 落岩撞击对行车舒适性的影响

控制行车速度为80 km/h,采用非一致桥面不平顺激励,计算了落岩撞击桥墩对行车舒适性的影响。两种工况下车体横向加速度和Sperling指标如表3所列。

表3 落岩撞击对行车舒适性的影响

由表3可知,落岩撞击桥墩时,车体横向振动加速度由0.36 m/s2增大到0.68 m/s2,增幅88.9%;行车舒适性变化较大,Sperling指标由1.42增大到3.06,从稍有振动变为振动强。

3.2 车速对行车舒适性的影响

采用非一致桥面不平顺激励,控制行车速度为40 km/h、60 km/h、80 km/h、100 km/h,研究不同车速下落岩撞击桥墩对行车舒适性的影响。不同车速下车体横向振动加速度和Sperling指标如表4所列。

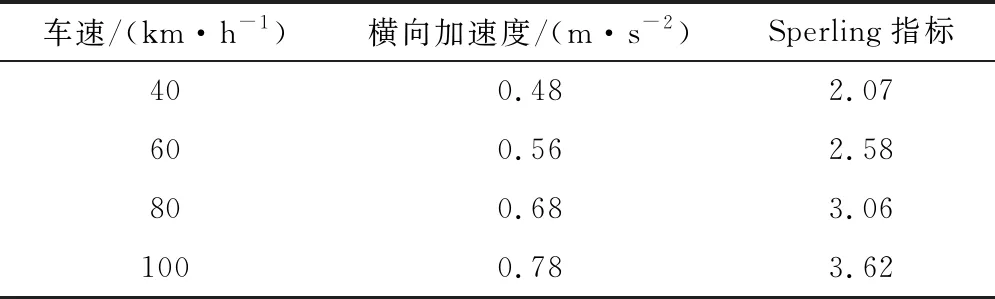
表4 不同车速下行车舒适性

由表4可知,车速对落岩撞击作用下行车舒适性影响较大。随着行车速度的增加,车体横向振动加速度和横向Sperling指标均增大,车速100 km/h的车体横向加速度和横向Sperling指标分别是车速40 km/h的1.63倍和1.75倍,说明车速增加会加剧车辆振动。

4 结论

建立了考虑落岩撞击影响的车-桥耦合动力学模型,采用非一致激励的方法输入桥面不平顺,研究了落岩撞击桥墩对车-桥振动和行车舒适性的影响,得出以下结论:

(1) 落岩撞击桥墩对大跨度连续刚构桥车-桥振动影响显著,落岩撞击下主梁跨中横向位移和加速度分别是无落岩撞击的2.05倍和2.71倍。

(2) 随着行车速度的增加,落岩撞击作用下大跨度连续刚构桥车-桥振动加剧,车速100 km/h时的桥梁横向位移和加速度峰值分别为车速40 km/h时的1.38倍和1.43倍。

(3) 落岩撞击对行车舒适性影响较大,在落岩撞击作用下,行车舒适性Sperling指标由1.42增大到3.06,行车舒适性降低。

(4) 随着行车速度的增加,行车舒适性Sperling指标增大,车速100 km/h的横向Sperling指标是车速40 km/h的1.75倍,表明行车速度对乘车舒适性影响较大。