异构密码系统中无对的混合部分盲签密方案

◆杨喜艳

（塔里木大学信息工程学院 新疆 843300）

随着网络技术的发展，伴随着信息输入，数据传输，网络资源共享等通信安全问题的产生，人们越来越注重信息数据的机密性和认证性。能保证密文的认证性和机密性的最为有效的措施为数字签密[1-2]。目前，签密方案多使用公钥加密技术和对称加密技术，但两种技术分别在加密速度和安全性方面有局限。因此，实际通信时，多采用混合加密[3-4]或者混合签密[5-10]的方法。混合加密包含公钥加密的密钥封装机制（key encapsulation mechanism，KEM）及对称密钥加密的数据封装机制（data encapsulation mechanism，DEM）。2009 年，混合加密技术被Li，Shirase 和Takagi[11]用于构建基于身份签密方案中，同时，还根据BLMQ 方案[12]构建了基于身份签密KEM 实例。2013 年，Li，Shirase 和Takagi[13]将签密TKEM 用于无证书领域，展示了无证书签密方案中可运用混合加密技术。为了证明构造的合理性，他们还根据BF 方案[14]构造出了一个无证书签密TKEM。此后，诸多学者对基于身份的混合签密[15-17]和无证书混合签密[18-21]进行了研究。

但是，在上述的混合签密方案中，用户是处于同一个密码体制中的。随着大数据和云计算的发展，跨平台的应用和操作越来越普遍。因此，适用于在不同密码体制间通信的异构密码系统就需要被考虑。近年来，许多学者研究了异构签密[22-27]。

在上述异构签密方案和混合签密方案中，签名人在对明文签名时是已知明文内容的。但在某些特殊的应用环境中，消息内容对于签名人需要具有盲性。在1982 年，盲签名被Chaum 首次提出。由此以后，诸多学者研究了盲签名[28-33]，一些学者还将盲签名扩展到了盲签密，提出了许多盲签密方案[34-38]。但现在可查阅的盲签密方案中通信双方采用同样的密码体制，这是不现实的。因此，本文构建的方案生成系统主密钥方式灵活，为用户提供了更多可能性。同时，本文方案采用混合签密技术，能够加密任意大消息，另外本文方案是部分盲签密，不仅满足所有盲签密的特性，而且选择部分明文消息进行盲签名，更加有利于实现消息拥有者的隐私保护。并在ROM 下，验证本文方案基于CDH 问题及DL 问题的保密、不可伪造、盲、不可追踪等特性。通过理论分析和数值实验分析，本文方案的计算效率明显更高，通信成本明显更低，所以本文方案具有更高的可行性。

1 基础知识

1.1 困难性假设

定义 1.计算Diffie-Hellman（Computation Diffie-Hellman，CDH）问题，已知 (P,aP,bP)∈G1，对任意未知的a,b∈，计算abP∈G1。

定义 2.离散对数（Discrete Logarithm，DL）问题，已知(P,aP)∈G1，计算a∈。

1.2 安全模型

在基于异构密码系统无双线性对的混合部分盲签密方案中，主要考虑两种攻击者A1,A2：A1对s2是未知的，但能更换用户公钥；A2对s2已知，但不可替换用户公钥。因此，A1,A2分别应具有在选取密文攻击下的不可区分和明文攻击下的不可伪造。

2 具体方案

系统建立算法.设G1,G2均为阶是q的循环群，P为G1的生成元。选择三个hash 函数：H3:{0,1}*→G1。(E,D)为对称加密技术中的加密及解密算法。s1,s2为系统主密钥，PKG 保密s1，并计算，KGC 保密s2，并计算P2=s2P。系统参数为:params={G1,G2,q,P,n,E,D,H1,H2,H3}。

IBC 密钥提取算法.写入用户身份IDA，PKG 产生用户私钥SA=s1QA，其中QA=H1(IDA)。

CLC 密钥提取算法.该算法分为以下三步：

（1）输入用户身份IDB，KGC 计算用户部分私钥DB=s2QB，其中QB=H1(IDB)，最后通过安全方式发给用户；

（2）用户随机选择xB∈；

（3）用户计算公钥PB=x BP和完整私钥SB=x B DB。

部分盲签密.M是消息拥有者，A是部分盲签名者，c*是公共信息，m是待签密的消息，部分盲签密算法如下：

（1）A随机选择r∈，计算R1=rQA，R2=rP，并将 (R1,R2)发送给M；

（2）M随机选择a∈，计算U1=aR1，U2=aR2，U3=a-1QA，h=H2(m,c*,U1,U2)，并将h发送给A；

（3）A计算h*=H2(h,c*,IDA,IDB)，S=(r+h*)SA，并将S发送给M；

（4 ）M计 算S*=a-1S，K=H3(P2QB,P2QB PB)，c=DEM.Enc(K,m)；

（5）M输出密文σ= (c,S*,U1,U2,U3,R1,R2)。

解签密.检验等式P1S*=(R2+Ph*)U3是否成立。若不成立，输出⊥，否则，解签密算法如下：

（1）B计算K=H3(DBP,S BP2)；

（2）B计算m=DEM.Dec(K,c)；

（3）B输出m。

3 安全性分析

3.1 正确性

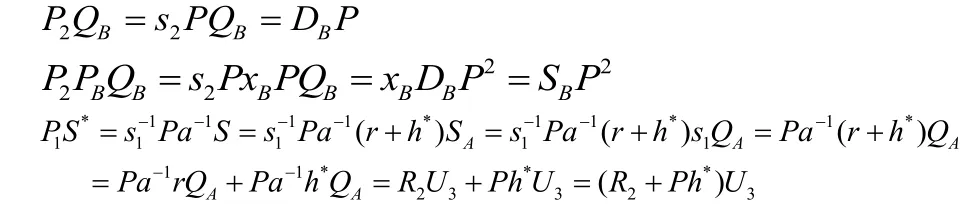
3.2 机密性

假设除了消息拥有者M和接收者B之外的任意第三方（假设是部分盲签名者A）能够从密文c中恢复出消息m。因为在部分盲签密阶段，M给A的是关于m的hash值，A只能通过密文c恢复出m，所以A必须通过计算对称密钥K恢复m。但是A仅仅知道(SA,R1,R2,r,h,S,h*)，而不知道B的秘密值xB，因此A通过K不可能恢复出m，因为A需要解决离散对数困难问题。由此可见，除了M和B外，其他用户不可能知道m。

3.3 不可伪造性

在本文方案中，即使A拥有r和SA，A需解决的困难问题是单向散列函数，所以通过h=H2(m,c*,U1,U2)不能恢复m，且A无法得知M选择的a，因此A不可伪造部分盲签密。

如果B称 (c,S*,U1,U2,U3,R1,R2)是来自M的密文，B想要通过S*=a-1S和S=(r+h*)SA恢复出a和r，并伪造 (U1,U2,U3,R1,R2)，即使B在信道上获取SA和h，但是B不知道公共信息*c，B需解决的是离散对数困难问题和单向散列函数困难问题，所以B不能通过S*=a-1S和S=(r+h*)S A恢复出a和r。因此B不可伪造部分盲签密。

如果M想要伪造一个合法的部分盲签密，首先，M不知道A的私钥SA，其次，M无法得知r，即使M在信道上获取SA，M需解决的是离散对数困难问题，所以M不可通过R1=rQA，R2=rP恢复出r。因此M不可伪造部分盲签密。

如果除M,,A B外的其他人想伪造合法的部分盲签密，即使他在公开信道上截获 (S A,DB,R1,R2,h,S,U1,U2,U3,c,S*)，但他对(s1,s2,x B,S B,r,a)是未知的，因此他不能伪造部分盲签密。

3.4 盲性

盲性指的是部分盲签名者在签密过程中对消息是不可见的。在部分盲签密算法中，M随机选择a∈，计算U1=aR1，U2=aR2，U3=a-1QA，h=H2(m,c*,U1,U2)，并将h发送给A。显而易见，A不知道需要签名的消息内容。

3.5 不可追踪性

不可追踪性指的是部分盲签名者不能通过需要签名的内容追踪到密文。如果B公开部分盲签密的密文(c,S*,U1,U2,U3,R1,R2)，即使A保留原始的签密数据 (R1,R2,h,h*,S)，但是A不能通过密文消息获得数据 (U1,U2,U3,S*,c,K)。因此，方案满足不可追踪性。

4 效率分析

本节通过理论和数值实验对效率进行分析。首先，进行理论分析。文献[34]、[35]、[36]均为盲签密方案，本节将对文献[34]、[35]、[36]及该文提出的方案的效率进行比较，主要比较对运算（P），指数运算（EP），点乘运算（MP），异或运算（OP）。由表1 可知，在签密阶段，文献[34]的方案比本文方案多7 个EP，2 个MP，2 个OP，文献[35]的方案比本文方案多1 个P，4 个EP，1 个OP，但是本文方案比文献[35]的方案多4 个MP。文献[36]的方案比本文方案多1 个P，1 个EP，但是本文方案比文献[36]的方案多1 个MP。在解签密阶段，文献[34]的方案比本文方案多6 个EP和2 个OP，文献[35]的方案比本文方案多3 个P，1 个OP，但是本文方案比文献[35]的方案多5 个MP。文献[36]的方案比本文方案多3 个P，但是本文方案比文献[36]的方案多6 个MP。由此可见，本文方案的计算效率明显比文献[34]、[35]、[36]更高。

表1 计算效率

其次，进行数值实验分析，采用C 语言的PBC 库对本文方案仿真模拟。在模拟过程中，群G1,G2的取1024bit，参数为a型椭圆曲线y2=x3+xmodq，通信者身份及消息取160bit 随机值。模拟环境配置如表2 所示。

表2 环境配置

为比较计算效率，对文献[36]的方案做相同仿真。仿真结果取60次的平均值，如图1 所示。因文献[34]、[35]明显比文献[36]和本文方案的计算效率高，因此无需对文献[34]、[35]做仿真。

由图1 可以清楚看出本文方案的计算效率明显比文献[36]更高，因此本文方案的可行性更高。

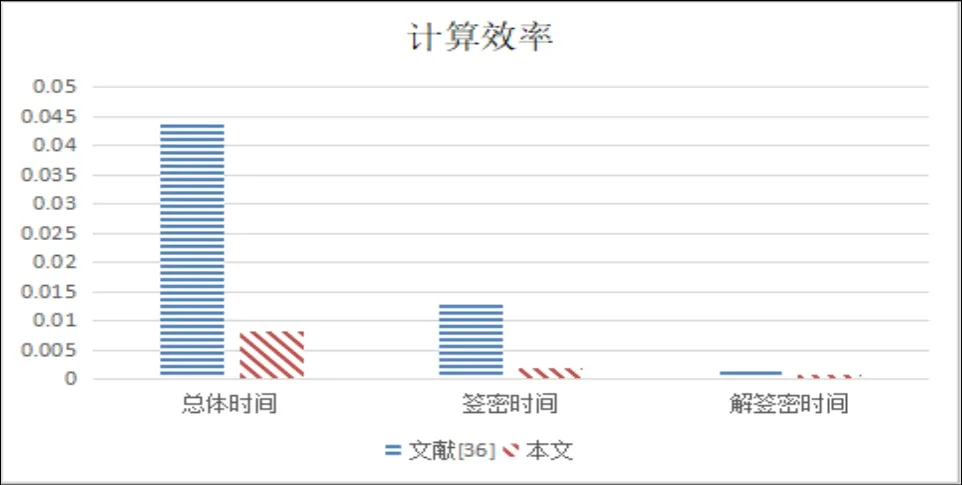
图1 计算效率

5 结论

在本文方案中，在不同密码体制中生成系统主密钥方式灵活，而且本文是部分盲签密，满足所有盲签密的特征。另外，对于任意大消息的签密，本文采用混合签密完成。同时，在ROM 下，本文方案有机密、不可伪造、盲、不可追踪等特性。经理论分析和数值实验显示本文方案更适用于实际环境。