直升机尾传动轴弹击损伤仿真与试验验证
赵思波,万振华,2,王 希
(1.中国航发湖南动力机械研究所,湖南 株洲 412002;2.直升机传动技术国防科技重点实验室,湖南 株洲 412002)
尾传动轴是直升机传动系统的关键动部件之一,其主要功能是将主减速器输出的功率和转速传递至尾桨,使得尾桨产生推力(或者拉力)以平衡主旋翼系统产生的反扭力矩。由于尾传动轴一般采用单传递路径进行设计,一旦尾传动轴失效而无法提供尾桨所需的功率和转速,直升机及其乘员的安全将面临严重的威胁。基于上述原因,国军标中明确要求,直升机尾传动轴需要进行抗弹击等损伤容限设计;第五代军用直升机则明确要求尾传动轴被12.7 mm口径子弹击中后,仍具备继续正常运转30 min的能力。
本文基于LS-DYNA显式动力学分析软件,参考国内外相关弹击研究方法[1-2],结合尾传动轴可能面临的弹击工况,建立了直升机尾传动轴弹击损伤仿真模型,并开展了部分弹击试验验证。同时,结合弹击仿真模型对弹击损伤的主要影响因素进行研究。
1 弹击仿真模型
1.1 几何模型
本文选取某型直升机尾传动轴为研究对象,该尾传动轴的外径为114.4 mm,内径为111.2 mm,长度为2~3 m。考虑到弹击仅对尾传动轴造成局部损伤,为减小计算规模、提高计算效率,本文选取长度为200 mm的尾传动轴轴段作为简化后的研究对象。
子弹一般由壳体、弹芯和弹药组成。由于本文主要研究弹药起爆后子弹弹芯对尾传动轴的弹击侵彻问题,因此主要关注子弹弹芯的几何结构形状,本文选取12.7 mm口径子弹弹芯进行研究,其几何模型[3]如图1所示。
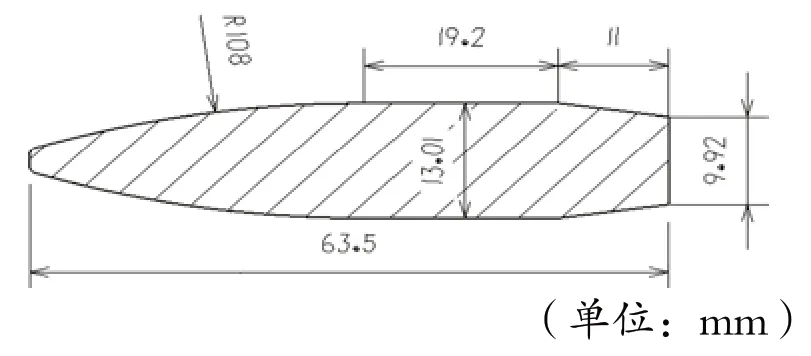
图1 12.7 mm口径子弹弹芯尺寸图
1.2 材料本构模型和失效模型
直升机尾传动轴一般采用机械性能优异且密度较低的铝合金材料。由于铝合金材料在弹击过程中涉及大应变、高应变率及材料失效等问题,因此选取工程中最常用的Johnson-Cook本构模型和失效模型对铝合金材料在弹击过程中的变形行为和失效行为进行描述。
Johnson-Cook本构模型如式(1)所示。

式中,σ为有效屈服应力,A为初始屈服应力,B为应变硬化模量,C为应变率强化参数,n为应变硬化指数,m为热软化参数,T*为相对温度,εp为有效塑性应变,·ε为等效塑性应变率,为参考应变率。
Johnson-Cook失效模型如式(2)所示。

式中,是失效应变,D1~D5是失效常数,σ*=-Rcr,Rcr是应力三轴度,是无量纲塑性应变率,T*为相对温度。
Johnson-Cook模型定义的单元损伤为:

式中:D为损伤参数,初始时刻D=0,冲击过程中当D≥1时材料失效; 为一个时间步的塑性应变增量。
12.7 mm口径子弹弹芯主体为高强度钢材质,考虑到弹芯的刚度和极限强度均远高于铝合金,子弹弹芯采用刚体模型,即在弹击过程中不考虑子弹的变形行为及失效行为。本研究中尾传动轴材料为2024-T3铝合金,高强度钢和2024-T3铝合金的本构模型参数如表1所示[4],2024-T3铝合金的失效模型参数如表2所示。

表1 高强度钢和2024-T3铝合金的本构模型参数

表2 2024-T3铝合金的失效模型参数
1.3 有限元模型
尾传动轴和弹芯均采用六面体单元进行网格划分,尾传动轴网格最小尺寸为0.75 mm× 0.75 mm ×0.55 mm,尾传动轴和弹芯的单元个数分别为128 538个和3 168个,有限元模型如图2所示。
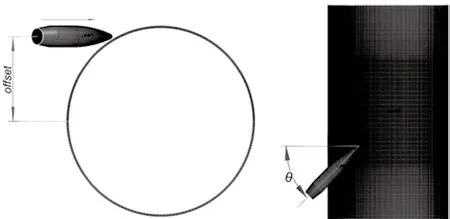
图2 尾传动轴和弹芯有限元模型
图2中offset为子弹弹道与尾传动轴轴线之间的距离,θ为子弹弹道线与尾传动轴横截面的夹角,通过控制offset和θ,可以确定子弹与尾传动轴的所有可能的相对位置关系。
1.4 初始条件及边界条件
在仿真过程中,子弹的初始速度设置为500 m/s。由于采用部分尾传动轴进行仿真,为消除反射应力波对轴段产生的干扰,对轴段两端边界上施加非反射边界条件,对轴段两端进行固支约束。在子弹与尾传动轴之间采用面接触侵蚀算法,轴管表面单元失效后将自动删除,子弹继续与剩余表面单元进行接触。
2 算例及验证
2.1 算例1:45°切边弹击工况
直升机尾传动轴主要承受扭矩载荷,在扭矩载荷的作用下,轴管表面任一点的最大主应力方向与轴线成45°夹角。根据文献分析及理论推导,当弹击后的轴管表面主裂纹方向(速度方向)垂直于主应力方向,则表面裂纹为I形裂纹,在扭矩作用下具有张开的趋势,推测此弹击工况有可能为最严酷工况。算例1中设置θ=45°、offset≈50.85 mm(在50.85 mm附近进行微调,使得弹击工况最严重)对该弹击工况进行模拟,并在轴管静置状态下开展弹击试验验证。
尾传动轴在上述工况下的弹击损伤仿真结果与试验结果如图3所示,弹击损伤仿真结果与试验结果吻合较好,弹击产生的可见裂纹主要集中在子弹入射孔和出射孔附近,弹击后尾传动轴在扭矩作用下很可能由于裂纹张开扩展而断裂。

图3 45°切边弹击损伤仿真结果(上)与试验结果(下)
2.2 算例2:60°切边弹击工况
直升机尾传动轴遭受弹击后继续承载运转时,可能的破坏模式不仅是弹孔周边裂纹扩展断裂,也可能是弹孔导致局部刚度下降使得结构发生屈曲失效。本项目团队的弹击摸底试验结果表明:切边条件(offset≈50.85mm)下,θ值越大,轴管表面破损越严重,其局部刚度下降越剧烈。考虑直升机尾梁对尾传动轴具有一定防护作用,算例2假设尾传动轴弹击工况最大θ=60°,针对该弹击工况进行仿真模拟,并在轴管静置状态下开展弹击试验验证。
尾传动轴在上述工况下的弹击损伤仿真结果与试验结果如图4所示,弹击损伤仿真结果与试验结果吻合较好,弹击损伤缺口相比45°入射工况急剧增大,同时轴管表面存在较大的凹陷和翘曲现象,弹击后继续承载运转时轴管具有局部屈曲使得弹孔两侧有靠近的趋势。

图4 60°切边弹击损伤仿真结果(上)与试验结果(下)
3 弹击损伤主要影响因素分析
3.1 入射偏移量offset对弹击损伤的影响分析
为分析入射偏移量offset对弹击损伤的影响,选取θ=0°和θ=45°两个入射角度,对不同偏移量下的弹击损伤进行统计,统计方法如图5所示,lx表示弹孔轴向尺寸,ly表示弹孔周向尺寸(入射孔与出射孔融为一体时,为方便对比,人为将弹孔划分为入射孔和出射孔区域,并按图5方式进行统计),结果如表3和表4所示。
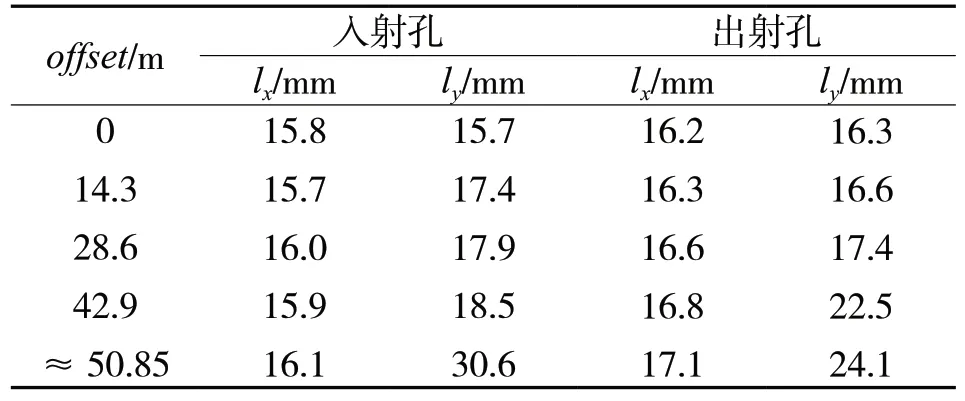
表3 0°入射时不同偏移量下的弹击损伤大小
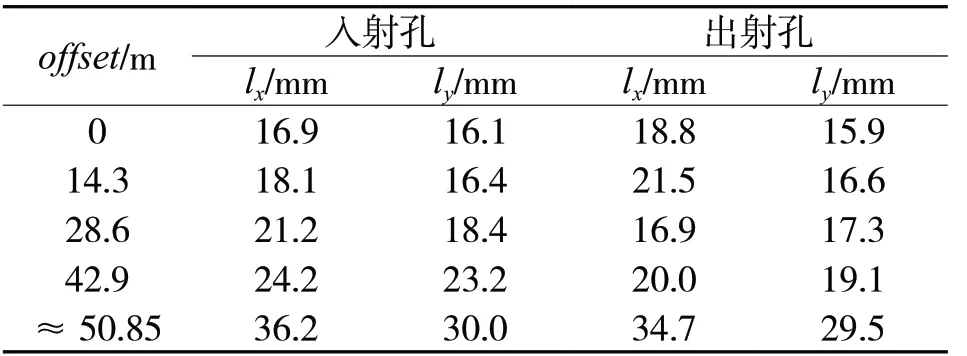
表4 45°入射时不同偏移量下的弹击损伤大小
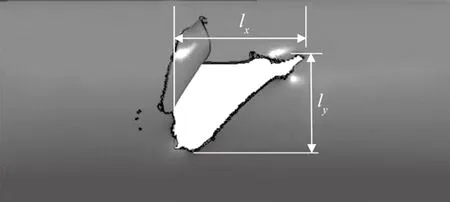
图5 弹击损伤统计方法
从表3和表4可知,弹击位置靠近轴管边缘前,弹击损伤度量值基本相当或略有增加;弹击位置为轴管边缘时,弹击损伤急剧增加,由此可知切边弹击工况相比非切边工况造成更加严重的弹击损伤。
3.2 入射角θ对弹击损伤的影响分析
为分析入射角θ对弹击损伤的影响,选取严酷的切边弹击工况,对不同入射角θ下的弹击损伤进行统计,结果如表5所示。
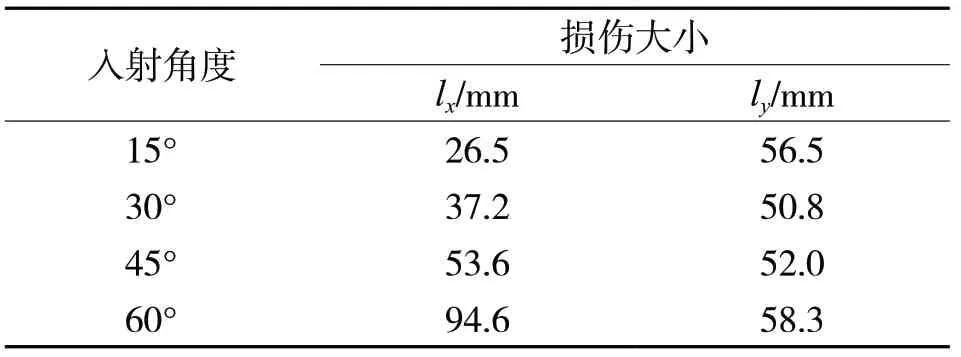
表5 不同入射角下的弹击损伤大小
从表5可知,切边弹击时,弹击损伤度量值随着入射角增加而快速增加,同时弹孔周围的凹陷和翘曲随着入射角增加而更加严重。由此可知切边弹击工况下,入射角θ越大,尾传动轴弹击损伤愈严重。
3.3 入射速度对弹击损伤的影响分析
为分析入射速度对弹击损伤的影响,选取切边45°弹击工况,对不同入射速度下的弹击损伤进行统计,结果如表6所示。
从表6可知,在切边45°弹击工况下,不同入射速度下的弹击损伤大小基本相当,入射速度对弹击损伤影响较小,主要原因是尾传动轴为薄壁结构,子弹穿透尾传动轴所损失的能量较小,因此只要入射速度足够使得子弹穿透轴管且弹道线不发生大的偏移,其损伤大小基本是相同的。
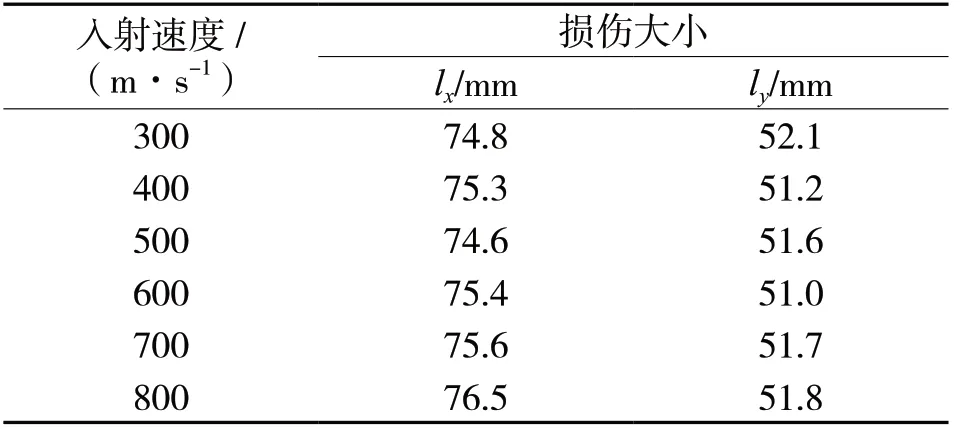
表6 不同入射速度下的弹击损伤大小
4 结束语
本文通过结合有限元仿真方法和试验方法对直升机尾传动轴弹击损伤进行了研究,得到了以下结论:
(1)采用LS-DYNA显式动力学分析方法建立的尾传动轴弹击损伤仿真分析模型可预测所有可能弹击工况下的弹击损伤,实验表明预测结果与试验结果吻合较好;
(2)仿真分析表明:弹击损伤随着入射偏移量增加而逐渐增加,弹击位置处于轴管边缘时损伤达到最大,同时弹击损伤也随着入射角增加而增加,但对子弹入射速度不敏感;
(3)尾传动轴最严酷的弹击工况为切边大角度入射工况,弹击试验及弹击后的承载运转试验应根据此工况进行开展,以保证直升机尾传动轴在极限弹击工况下均满足安全运转需求。考虑到尾传动轴有尾梁蒙皮等保护层,最大入射角需要根据实际情况进行确定。

