航空发动机叶片数控智能磨削加工技术研究

袁 明

(中国航发哈尔滨东安发动机有限公司，黑龙江 哈尔滨 150001)

0 引言

一个国家所具备的航空能力是显示科技发展水平的主要指标之一。对于飞机来说，动力系统是飞行的基础与前提，发动机作为飞机的动力系统，受到了国家的重视。航空发动机由多个部件构成，最关键的部件为叶片，其数量占比达到了40%以上。常规情况下，航空发动机应用叶片对气体进行压缩和膨胀，以最大效率产生动力，帮助飞机完成相应的任务。航空发动机正常作业时，叶片运动形式为高速旋转，承担的载荷较大，这对叶片质量和性能等提出了极高的要求，如耐高温性能和耐磨损性能等[1]。以涡喷风扇发动机为例，其运行总压比约为40，此时，叶片转速能够达到12 500 r/min，燃烧室温度能够达到1 720 K，再加之工作环境较为恶劣，致使叶片失效概率急剧攀升。在航空飞机事故中，叶片失效造成飞机事故概率占比达到了80%以上，而叶片失效主要原因为加工质量存在缺陷，如加工工具精度差和表面粗糙度差等，由此可见，如何提升叶片加工质量是保障航空发动机稳定运行的关键。

随着航空发动机的不断升级与发展，叶片的形状也逐渐变得复杂，这对叶片加工技术造成了较大的挑战。而磨削加工技术是叶片制造过程中不可或缺的环节，其不但可以去除叶片表面刀痕，还可以提升叶片表面质量，以此达到精加工效果[2]。但是已有航空发动机叶片数控智能磨削加工技术无法满足叶片质量与精度的需求，因此提出新的航空发动机叶片数控智能磨削加工技术，制造更加精密的叶片，保障航空发动机的正常运行，降低飞机故障发生率。

1 航空发动机叶片数控智能磨削加工技术

1.1 叶片数控智能磨削加工轨迹规划

对于叶片数控智能磨削加工来说，合理的轨迹规划至关重要，不但可以提升数控计算效率，也能满足叶片磨削加工精度需求。选取参数线法规划叶片磨削加工轨迹[3]，其具备操作简单和运算效率快等优势。在加工过程中，数控车床刀具主要沿着叶片曲面的u线或者v线走刀。在叶片磨削数控智能加工轨迹规划过程中，最关键的环节为走刀步长与加工带宽计算。

其中，走刀步长计算公式为

(1)

L为叶片磨削加工走刀步长；ε为给定的加工误差极限；kf为叶片磨削中插补段沿着走刀轨迹f的法曲率。

加工带宽计算公式为

(2)

d为叶片数控磨削加工带宽；R为数控砂带轮的半径；εh为允许最大残留高度；kb为叶片表面沿轨迹方向b的法曲率。

以计算得到的走刀步长及加工带宽为基础，根据参数线法生成叶片磨削加工轨迹[4]，为叶片数控加工提供支撑。

1.2 叶片磨削加工余量计算

航空发动机叶片刚性较差、壁较薄和易变形等特点，在制作加工后仍然存在超差区域，加工余量分布也不均匀，对叶片后续磨削加工造成了一定的阻碍。因此，为了提升叶片加工精度，需要对叶片磨削加工余量进行提取与计算[5]。

叶片磨削加工余量提取与计算流程如图1所示。

图1 叶片磨削加工余量提取与计算流程

如图1所示，利用三坐标检测方法对叶片表面数据点进行采集，呈现1张曲面网格形式，数据点数量为(m+1)×(n+1)，其中，m+1为截面数量；n+1为截面上的数据点[6]。设置截面线方向与叶身长度方向为u与v，对应次数分别为k与l，以上述数据为基础，重构叶片模型，表达式为

(3)

p(u,v)为重构后的叶片模型；di,j为数据点i与j之间的距离；Bi,k(u)与Bj,l(v)分别为在u与v方向重构的B样条曲面。

依据规划好的刀路轨迹计算刀触点p(r,n)，其中，r为刀触点的径向矢量，n为刀触点的法向矢量。为了方便研究的进行，以叶片理论模型作为参照，其截面线与叶身长度方向表示为X与Y。经过基准重合后，获得经过刀触点，方向为法向矢量方向的直线，表示为

L=r1+δ×n

(4)

L为直线矢量方程；r1为检测坐标系下的径向矢量；δ为辅助系数，与直线长短紧密相关。

将式(3)与式(4)联立即可获得交点p′，通过计算刀触点与交点之间的距离(不为0)，从而确定叶片的磨削加工余量，表达式为

(5)

通过上述过程完成了叶片磨削加工余量的提取与计算[7]，为后续叶片数控智能磨削算法的推出提供精准的数据支撑。

1.3 叶片数控智能磨削算法

上述过程获得的叶片磨削加工轨迹与磨削加工余量只是叶片制作加工的第1步，但是这些数据无法直接应用于数控机床，需要对其进行适当的处理[8]。为了实现叶片的数控智能加工，必须对数控机床加工过程中的运动姿态进行全面控制，推出对应的叶片数控智能磨削算法。

叶片数控智能磨削算法包含3个控制模型，分别为数控机床转轴、直线轴与压力轴运动控制模型。以叶片理论模型为基础，构建工件坐标系，记为OPXPYPZP，使其与数控机床坐标系保持同样的姿态。为了保障叶片刀触点矢量与磨头刀架矢量保持方向相同，需要将卡盘绕X轴旋转A角，绕Y轴旋转B角，并精确计算旋转角，即可完成转轴运行控制[9]。旋转角计算公式为：

(6)

(7)

N0=[nx0,ny0,ns0,0]T为在工件坐标系下，刀触点法向矢量；N1=[nx1,ny1,ns1,0]T为叶片旋转A角后刀触点的法向矢量。

数控机床直线轴控制主要是对旋转变换后刀触点的坐标数值进行计算，其决定着刀具是否能够按规划轨迹进行运作，不但影响着叶片磨削加工精度，也会影响磨削的效率[10]。

假设旋转后工件坐标系中刀触点为R2=[x2,y2,z2,1]T，依据数控机床坐标与工件坐标系的关系，通过坐标转换计算刀触点在数控机床中的坐标，计算公式为

(8)

航空发动机叶片磨削加工实质上是一种柔性抛磨过程，为了保障材料具有一定的去除率，必须对叶片施加一定的法向接触压力w，这也是压力轴的运行控制重点[11]。随着磨削加工余量的变化，相应地施加载荷也存在着较大的不同。为了满足叶片加工精度的需求，应该根据刀触点磨削加工余量确定磨削参数，以此为基础，调节数控机床压力轴的接触压力[12]。

在叶片磨削加工过程中，材料去除率为

rk=Cg·(Vb)x1·(Vw)x2·(F)x3

(9)

rk为材料去除率；Cg为磨削过程中，修正常数、阻力系数与耐用度系数的乘积；Vb为砂带线速度；Vw为叶片进给速度；F为刀触点p的法向压力；x1、x2和x3为辅助计算参数。

以式(9)计算结果为基础，确定磨削压力计算公式，即

(10)

x0为辅助计算参数，取值范围为0～1。

上述过程完成了数控机床运行姿态的全面控制，为叶片磨削加工提供良好的控制性能[13]。

1.4 叶片加工反变形误差补偿

由于环境、器械等多种因素的影响，叶片磨削加工存在着些许误差，导致叶片发生一定的弯曲变形，如叶片向上或者向下偏移、叶根偏移量较大等[14]。上述情况均会影响叶片的加工质量，故需要对其进行反变形误差补偿，常规情况下，叶片在加工去除余量后，叶冠会发生δ变形，此时为了补偿δ变形[15]，刀位点应该向相反方向进行偏移补偿，还需要满足叶片表面光滑性，因此需要满足下述条件，即

a-x≥δ

(11)

a为单步加工量；x为刀位点偏移补偿量；a-x为实际磨削深度。

特别地，对叶片进行进一步精加工时，为了确保实际磨削不会超过理论数值[16]，还需要满足下述条件，即

a-x≤d

(12)

d为当前时刻叶片余量。

通过上述过程完成了航空叶片数控智能磨削加工，有效地提升了叶片制作加工的精度。

2 实验与结果分析

2.1 实验准备阶段

为了验证本文技术的应用性能，选取七轴联动数控砂带磨床作为实验设备，并配备海克斯康三坐标测量机、TR200粗糙度仪等装置。实验关键设备——七轴联动数控砂带磨床主要技术指标如表1所示。

表1 七轴联动数控砂带磨床主要技术指标

依据上述实验设备技术指标，结合实验需求，对设备参数进行科学、合理的设置，并进行测试，在测试合格后，应用该设备进行航空发动机叶片数控智能磨削加工实验。

2.2 实验方案制定

为了避免航空发动机叶片磨削加工过程出现干扰因素，对叶片进行适当的区域划分，具体划分结果如图2所示。

图2 叶片区域划分

依据叶片材料的特性，需要对其进行多次的测试磨削，确定最佳叶片磨削线速度。由于叶面每个磨削区域的纹理以及余量存在着较大的不同，也需要进行相应的工件进给速度设置。

2.3 实验结果分析

以上述选取的实验设备、划分的实验区域为基础，利用P180红色尼龙砂带进行粗磨削加工，利用P240蓝色尼龙砂带进行细磨削加工，在加工后对其误差进行一定的补偿，获得航空发动机叶片。采用三坐标测量机对其加工精度进行检测，以此显示本文技术的应用性能。

通过实验获得叶片型面磨削加工前后示例，如图3所示。

图3 叶片型面磨削加工前后示例

由图3可知，在磨削加工后，叶片型面粗糙度得到了极大的改善，测量粗糙度数值为0.4 μm，满足叶片磨削加工需求。

叶片边缘磨削加工情况，需要通过OGP边缘投影仪来检测。以获得的投影图像为基础，计算叶片边缘磨削加工误差，如图4所示。

图4 叶片边缘磨削加工误差

由图4可知，叶片1与叶片2磨削加工误差结果较为相近，在标准误差限值范围内。

叶片根部磨削加工过程较为复杂，对磨削线速度的要求较高。根据已有文献研究可知，最佳叶片根部磨削线速度为20 m/min。为了验证本文技术的应用效果，对叶片根部进行随机点位采样，对其粗糙度进行测量及比较，具体结果如图5所示。

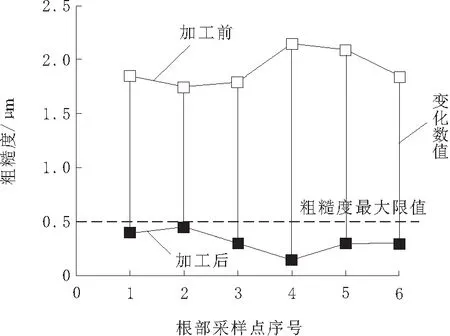
图5 叶片根部粗糙度

由图5可知，经过磨削加工后，叶片根部粗糙度得到大幅度降低，并且低于粗糙度的最大限值。

上述实验数据表明，应用本文技术后，叶片型面、边缘与根部均满足加工精度需求，充分验证了本文技术应用效果较佳。

3 结束语

为了满足现今叶片质量与精度的需求，开展了航空发动机叶片数控智能磨削加工技术研究，并通过实验验证了本文技术的可行性与有效性，为叶片制作加工提供技术支撑，也为航空领域发展提供助力。