一种应用于法兰盘装配的定位方法

杨泽伟，祁宇明，2

（1.天津职业技术师范大学机器人及智能装备研究院，天津 300350；2.天津职业技术师范大学天津市智能机器人技术及应用企业重点实验室，天津 300350）

随着信息科学通信技术的发展及在制造业中的广泛应用，工业制造相关生产正朝着智能化、自动化的方向发展[1]，工业机器人在其中起到了重要作用。传统的工业机器人只能按照已规划好的轨迹运行，主要应用于一些结构化情景，在喷涂、抛磨、装配等非结构化场景中，仍需人工配合作业，自动化程度不高[2]。而机器人结合视觉传感器后，可以对目标工件进行定位，提高了机器人在装配等作业场景中的自动化程度。现阶段，在工业领域中应用的定位方法主要有基于点特征类算法[3-5]、基于模板匹配算法[6-7]和基于深度学习类算法[8]。近年来，基于深度学习的目标检测与定位算法成为主流方法，此类算法常用的有R-CNN、Fast-RCNN、Faster-R-CNN、YOLO、SSD等，这些算法与传统方法相比，虽然精度高，对遮挡、噪声、光照有较强的鲁棒性，但是训练时计算机所需内存空间大，检测效率低，定位精度依赖于训练模型的精确度，这极大地限制了其应用[9]。针对法兰盘的形状特点，本文提出一种基于单目相机的定位方法。该方法可以快速地对法兰盘进行定位，解决了当法兰盘在传送带上随意摆放时法兰盘的定位问题，同时为法兰盘和圆盘类工件的定位问题提供了思路。

1 图像预处理

1.1 工件图像二值化

工业相机采集到的图像为RGB彩色图像，对三通道依次进行处理耗时较长。为了满足系统的实时性，采用均值加权法将原始图像灰度化为单一通道的图像。因需使用连通域分析对法兰盘的孔洞特征进行提取，故先将图像进行二值化处理。Qtsu自动阈值算法对灰度直方图为双峰分布的图像分割效果较好，且计算量较小，故本文采用Qtsu自动阈值法对图像进行二值化。Qtsu自动阈值法将0～255的每个整数值先假设为阈值，首先计算这256个值作为阈值时，前景与背景的灰度级方差，然后计算前景方差与背景方差的加权和，加权和最小的灰度值为该图像的分割阈值[10]。二值化后的图像中存在一些小的弧形连通域，会对孔洞特征的提取造成误差，故将二值化的图像做开运算，将一些小连通域消除，减少面积较小的连通域对连通域分析的干扰[11]。预处理的结果如图1所示。其中，图1（d）为对二值化进行开运算后的图像，是将图1（c）中的细小连通域去掉的结果。

图1 图像预处理

1.2 工件图像边缘检测

常用的像素级边缘提取算法有Sobel算子、Canny算子、LOG算子、Robert算子等。其中，Canny算子是一种满足最有准则的边缘算子，其检测结果包括了更多的边缘信息[12]。使用Canny算子提取到像素级边缘，为了提高定位的精度，需要对得到的边缘进一步处理得到亚像素边缘。目前，亚像素边缘提取的方法主要有矩方法、曲线拟合法、插值法。其中，矩方法的精度较高，本文使用矩方法中的Zernike矩进行亚像素边缘细化。亚像素边缘阶跃模型如图2所示。图2中：h为背景的灰度值；k为阶跃灰度；l为圆心与边缘的垂直距离；Φ为x轴与边缘垂线的夹角。

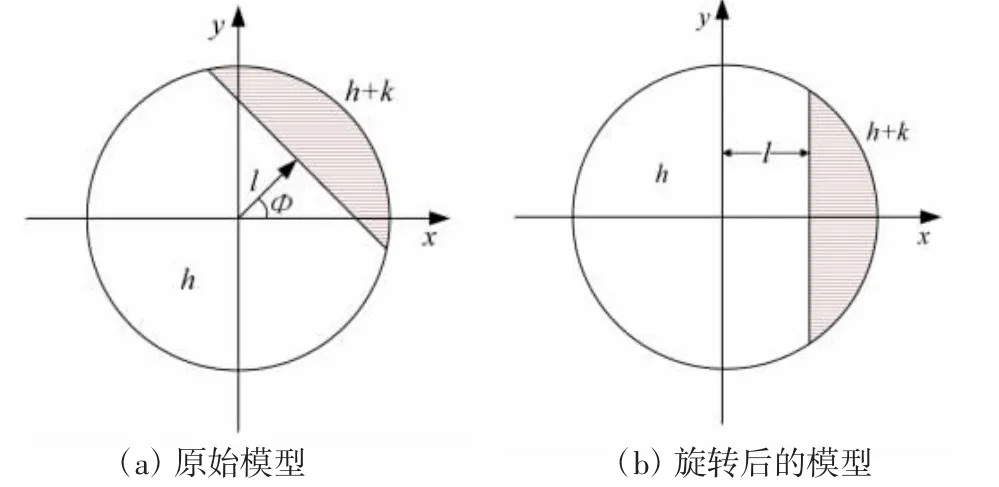
图2 亚像素边缘阶跃模型

Zernike的掩模为5×5，根据文献[13]的方法，计算出h、k、l、Φ等参数后，通过式（1）选择满足条件的边缘点

式中：μ1为第1类中k的平均值；μ2为第2类中k的平均值；μ为所有k的平均值。

计算类间方差

当σ取得最小值时，得到的阈值为最佳阈值，也就是ε的最佳取值。由于模板的放大效应，单位圆的半径变为N/2，修正后的亚像素边缘坐标为

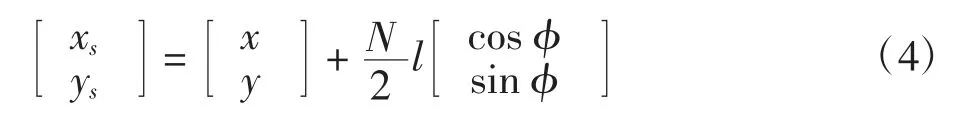
式中：（xs，ys）为亚像素边缘；（x，y）为Canny算子提取的边缘；N为模板的大小。

亚像素边缘提取的结果如图3所示。

图3 亚像素边缘

1.3 孔洞特征提取

先对二值化后的图像进行连通域标注，得到所有连通域后，通过面积作为阈值得到法兰盘的孔洞区域。连通域标记算法主要有像素标记法、区域增长等。本文采用八邻域连通域标注[14]，连通域标注的结果如图4（a）所示。将通过面积阈值得到的孔洞区域设为ROI区域，在每个感兴趣区域内提取轮廓，根据轮廓点集分别计算它们的细长度。细长度是基于区域的形状描述，使用旋转卡壳法[15]得到ROI区域轮廓的最小外接矩形如图4（b）所示。

图4 孔洞特征提取

用其长边除以短边得到细长度。圆孔的细长度接近1，而长圆孔的细长度＞1，因此可以通过比较细长度识别法兰盘上的圆孔与长圆孔。

通过预处理得到工件的二值化图像，对二值化图像进行边缘提取后，得到法兰盘的亚像素边缘，提取的边缘用于最小二乘拟合，并对图像的孔洞特征进行提取，得到的孔洞特征用来对法兰盘的旋转角度进行粗定位。

2 工件定位

2.1 坐标系转换

为了实现机械臂分拣装配工件的任务，需要进行摄像机标定。将投影到相机平面的像素坐标点投影到三维世界坐标系中，确定相机坐标系与世界坐标系的相互转换关系。本文相机标定的模型为针孔模型，像素坐标与世界坐标系的映射关系为

式中：ZC为尺度参数；u、v为像素坐标；XW、YW、ZW为世界坐标；fx、fy、u0、v0均为相机内参数；R为旋转矩阵；T为平移矩阵；R与T均为相机的外参数矩阵。

法兰盘的厚度是已知的，故此时ZW相当于已知。先将参数矩阵合并为

再将ZW提取出来，得到

此时等式两边向量的维数相同，在等式两边乘以参数矩阵的逆矩阵得到像素坐标中的点对应的世界坐标。

2.2 位置检测

由于法兰盘突出法兰的边耳轮廓会对圆的拟合造成误差，需要将边耳轮廓去除。先使用Shi Tomasi角点检测算法[16]将法兰盘边耳轮廓处的4个拐点检测出来，拐点提取如图5所示。

图5 拐点提取

检测出4个拐点后计算其中1个拐点与其他拐点之间的距离，然后对求出的距离进行排序，计算其中距离排在中间的点与该点之间连线的直线方程，直线方程为

对轮廓中的像素点进行约束，约束条件为

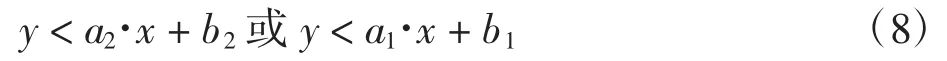
式中：（x，y）为轮廓里像素点的坐标。

将不满足上式的像素点删除，即将2条直线包围区域内的像素点去除掉，得到的轮廓如图6所示。

图6 去除边耳后的轮廓

圆拟合常用的方法有霍夫圆检测法、最小二乘拟合法、代数拟合法等。霍夫圆检测法虽然可以检测出圆，但其存在计算量较大，检测精度不高等缺点。代数拟合法虽然精度较高，但计算量较大，难以满足实时性的要求。基于最小二乘法圆拟合算法可以较好地提取圆信息[17]。因此，本文使用最小二乘法对边缘像素进行圆拟合。圆的一般方程为

式中：a、b、c为3个待求的未知量。

待拟合的点集为1.2节通过Zernike矩方法得到的轮廓像素点集（xi，yi），i∈（1，2，3…n），n为边缘轮廓像素点的个数。残差平方和F（a，b，c）可以表示为

为了得到使残差平方和最小的a、b、c 3个参数，对3个未知参数求偏导，并令其值为0，其计算式为

将式（9）代入式（10）中，得

将拟合点集即边缘点集（xi，yi）代入式（11）中，得到a、b、c参数的三元一次方程，将其求解得到a、b、c未知参数的值，再通过式（12）求得圆心和半径的值为圆拟合的结果如图7所示。

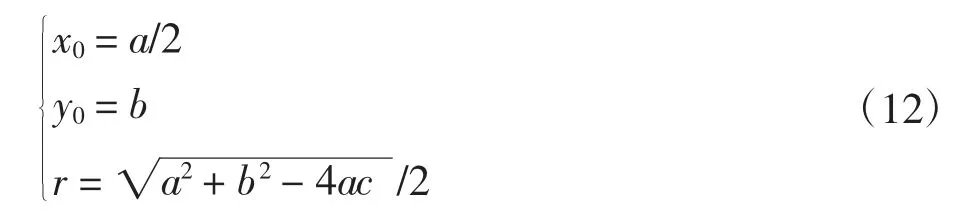
图7 最小二乘拟合结果

得到中心点坐标后，通过2.1节中的坐标转换得到法兰盘中心点在世界坐标系中的坐标位置。

2.3 旋转角度检测

为了使机械臂将工件放置在正确位置，需要获取工件的姿态信息，由于法兰盘的形状对称，水平地放置在传送带上，故只需获取法兰盘绕其中心轴的旋转角度，其具体步骤如下。

（1）旋转角粗定位

在1.3节已识别出长圆孔区域，长圆孔中心位置的坐标值通过统计特征矩计算，长圆孔的中心即其重心，重心的计算公式为

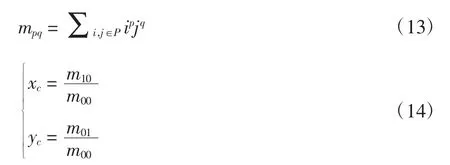
式中：mpq为像素点横坐标p次方与像素纵坐标值q次方的积分；P为长圆孔区域的像素点集；xc、yc分别为长圆孔重心的横、纵坐标。

根据重心坐标计算通过2个重心直线的倾斜角度，该倾角为输出法兰盘旋转角度的粗定位。倾角θ的计算公式为

式中：（xc1，yc1）、（xc2，yc2）分别为2个长圆孔重心的横、纵坐标。

（2）旋转角精定位

本文使用基于区域灰度值的模板匹配对输出法兰盘的旋转角度精定位，该方法具有较高的鲁棒性，是将模板从左到右，从上到下与待检测图片中与模板重合的部分进行相似度计算。本文采用归一化互相关算法——NCC算法，NCC算法对光照强度的线性变化适应性强，抗干扰性能较好[18]，其计算公式为

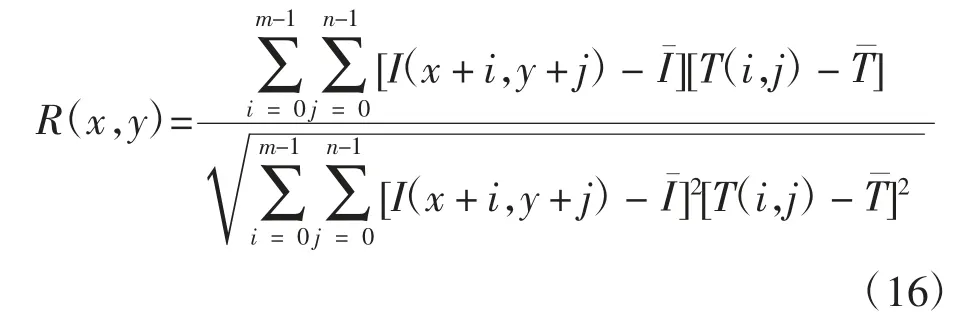
式中：R为待检测图像与模板重合的部分与模板图像的相似度；（x，y）为待检测图像中被模板覆盖区域左上角的像素点；n、m为模板图像的高与宽；I（x+i，y+j）为待检测图像中像素点（x+i，y+j）的像素值；T（i，j）为模板图像中像素点（i，j）的像素值；I¯为待检测图像被模板图像覆盖区域的平均像素值；T¯为模板图像素的平均值。

该方法较明显的缺陷是当工件发生旋转时，模板图像不能准确地匹配出待检测图片中要匹配的位置，造成机械臂无法抓取到工件，从而使算法失效。因此，对该算法进行改进，将输出法兰盘的灰度图像旋转[θ-1°，θ-0.9°，θ-0.8°，…，θ+0.9°，θ+1°]，图像旋转的步长为0.1°，步长太大会影响定位的精度，而步长太小会增加计算量和系统处理时间，故选择步长为0.1°，θ为上节中得到的直线倾角，然后将旋转得到的20张图像再与水平位置子图进行匹配，水平位置子图如图8所示。

图8 水平位置子图

匹配后每幅图像都会得到一个最大的R值，将得到的20个R值进行比较，R值最大的图像就是与水平子图匹配结果最好的图像，其角度β就是工件与水平位置的角度，即工件绕其中心轴的旋转角度。模板匹配结果如图9所示。

图9 模板匹配结果

对法兰盘进行定位得到法兰盘中心的空间坐标及法兰盘绕轴心的旋转角度，从而得到工业机器人的抓取位置及放置时机械臂末端工具的旋转角度。

3 实验

本文选用型号为MH2520S的工业镜头，该镜头焦距为25 mm，工业相机为大华12CG-E面阵彩色相机，相机的分辨率为1 280×960。相机固定在拍摄位置时，拍摄法兰盘平面的视野为80 mm×60 mm，此时相机的拍摄精度为0.25 mm/pixel。使用Intel Core CPU，16 GB RAM的计算机平台对图像进行处理，软件测试平台为Pycharm及OpenCV4.4库。为验证本文提出的基于单目相机的定位方法的有效性，将工件分别旋转至-90°、-45°、0°、45°、90°，并摆放在不同位置，通过工业相机采集工件在这5个角度的图像。通过对图像进行处理得到工件中心位置和绕主轴的旋转角度，将其与工件的实际旋转角度和位置进行比较，算法有效性验证如表1所示。

表1 算法有效性验证

由表1可知，旋转角度最大误差为0.1°，平均误差为0.08°，中心位置的定位误差＜0.3 mm可以满足工件装配的精度。根据表1中程序运行时间可知程序5次运行的平均总时间为377.54 ms，说明本文的方法能够快速定位，并获得法兰绕主轴的旋转角度，满足了机械臂对法兰盘抓取和装配的速度要求。

为了验证本文所提方法的稳定性，将法兰盘随意摆放在传送带上，采集50张处于不同位置的法兰盘图像，使用采集到的图像对其进行定位，得到的算法稳定性验证如表2所示。

表2 算法稳定性验证

由表2可知，在多次测试后，平均定位误差均较小，说明算法的稳定性能较高。

4 结语

本文提出一种基于单目相机的快速识别及位姿估计方法。该方法可以对传送带上任意摆放的法兰盘进行快速定位：首先对法兰盘进行亚边缘像素提取，然后使用最小二乘法对法兰盘边缘进行圆拟合，实现了对法兰盘中心的精确定位；通过模板匹配法获得法兰盘绕主轴的旋转角度。本算法计算量小，位姿检测用时少，精度高。本文所使用的方法还可以应用到处理不同的法兰盘和圆盘形工件上。需要指出的是，由于单目相机只能提取较少的图像信息，下一步的研究将使用基于双目视觉的位姿估计算法，利用本文提取出的特征点对法兰盘的6D位姿进行估计。