基于确信可靠度的离子推力器可靠性分析和试验设计

李 婧，陈世舜，贾艳辉*，李 娟，陈娟娟，张兴民，孙小菁

（1.兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000；2.北京航空航天大学，北京 100191）

0 引言

离子电推进是目前小行星探测应用的主要电推进技术之一。由于离子推力器的推力较小，必须稳定运行较长时间才能满足任务总冲。相比于现行任务指标参数，小行星探测用离子推力器服役时长要求成倍提升，长寿命、高可靠需求日益迫切。另外，由于探测器的飞行轨道距离太阳远近不一，太阳帆板输出功率也不相同。为了与不同太阳距离下太阳帆板输出功率的大小相适应，离子推力器功率须能在指定功率范围内进行多工作点调节[1]。再者，受研制周期和研制成本的限制，只能采用1~2台离子推力器产品进行地面长寿命验证试验，且传统1∶1试验的方式由于发射前可能无法完成试验已不再适用。因此，多工况模式、高可靠寿命、极端小子样条件下离子推力器可靠性评估与长寿命地面试验验证成为当前亟需攻克的关键技术之一。针对上述研究现状，结合离子推力器服役过程中性能退化的不确定性，本文基于确信可靠度理论进行LIPS-300离子推力器的可靠性评估建模和试验验证方案的设计。

1 确信可靠度理论与FPMA方法

1.1 确信可靠度理论

确定可靠度定义为系统的状态变量处于可行域中的机会。在可靠性工程中，状态变量通常是指可以通过试验、物理模型或在线监测得到的物理量，可行域是指使系统功能不完全丧失的状态变量的取值空间[2]。确信可靠性理论以概率论、不确定理论、机会理论为数学基础，基于可靠性科学原理，建立确信可靠性度量框架，实现对于功能、性能与不确定性的有效度量。

为了定量描述产品的性能变化与故障规律，确信可靠性理论遵循可靠性科学最基本的三个原理：裕量可靠原理、退化永恒原理和不确定性原理。裕量可靠原理：客体的性能裕量决定着客体的可靠程度；退化永恒原理：客体性能沿退化时间进行不可逆的退化；不确定性原理：客体的退化过程与性能裕量是不确定的。三个原理可以用三个方程表示：

式中：G(·)和F(·)表示特定函数关系。裕量方程表明，裕量M本质上是性能特性参数P到性能阈值Pth的距离，裕量大于0则产品可靠。退化方程描述了产品的确定性的退化规律，给出了产品性能特性P与系统内在属性X、外在属性Y、物理时间t以及退化时间T的函数关系。度量方程用概率测度、不确定测度等数学测度μ综合度量产品的各类不确定性，最终给出产品的可靠度R。

1.2 FPMA

FPMA是一种有序地对产品功能、性能及裕量进行分析的形式化方法。其分析流程如图1所示。

图1 FPMA分析流程图Fig.1 FPMA analysis process

根据性能参数的重要性等级，确定推力、比冲和放电损耗为推力器的关键性能参数，而离子推力器工作推力、比冲和放电损耗均与屏栅电流（功率）相关。根据失效模式、机制及影响分析，加速栅小孔溅射刻蚀引起的电子反流失效为影响屏栅电流输出最大的损耗型失效模式，也是当前已明确的LIPS-300离子推力器的主要失效模式。针对电子反流失效，电子反流极限电压可作为表征电子反流失效的可靠性性能参数（为作区别，后文中性能参数均指可靠性分析用性能参数，与推力器性能参数含义不同），该参数有明确的退化规律和可检测阈值（加速栅电压），因此可作为关键性能参数。

确定关键性能参数后，必须对其参数特性及性能阈值进行分析。关键性能参数分为望大（Larger-The-Better，LTB，性能参数低于失效阈值时发生失效）、望小（Smaller-The-Better，STB，性能参数超过失效阈值时发生失效）或者望目（Normal-The-Better，NTB，性能参数低于下限或超过上限时失效）三类，根据电子反流极限电压的特征将其归为望大类参数，如表1所列。

表1 关键性能参数类别Tab.1 List of key performance parameter attributes

2 裕量、退化和可靠性建模

2.1 裕量建模

由于电子反流极限电压为负值，当电子反流极限电压的绝对值超过加速栅电压时，即认为发生了电子反流失效，基于上述分析，可得推力器的裕量模型为：

式中：Va为加速栅电压；Vm为电子反流极限电压；MVm为电子反流极限电压的性能裕量。

接下来须建立电子反流极限电压的性能方程，明确电子反流极限电压与推力器各参数之间的关系。加速栅负电位的作用是防止中和器发射的电子进入推力器内部，而加速栅最低电位出现在加速栅中心孔处，称为加速栅鞍点电势。因此，应先从加速栅鞍点电势的角度建模，构建电子反流极限电压的性能方程。

考虑空间电荷影响的加速栅鞍点电势为[3]：

式中：da为加速栅直径；ta为加速栅厚度；Vbp为下游等离子体电势；ld为等离子体电势面到加速栅的距离；Vdp为放电室等离子体鞘层电势；le为束流离子的有效加速距离；ΔV为空间电荷产生的电势降。各参数的表达式如下。

（1）空间电荷产生的电势降ΔV为[4]：

式中：Ibs为单个加速栅孔内的离子束电流；ε0为真空介电常数；db为加速栅孔内的离子束直径，MXe为氙原子质量；e为电子电荷量；Vsp为不考虑空间电荷影响的加速栅鞍点电势。

考虑最严苛的情况，假设加速栅中心孔处的离子束电流密度值最大。根据Child-Langmuir定律[5-6]，对于氙离子推力器，加速栅孔内的最大电流密度为：

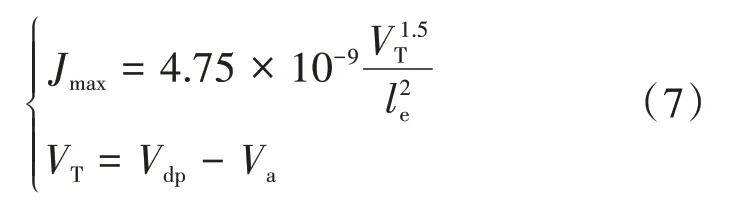
式中：Jmax为最大电流密度；VT为净加速电压。

离子束的直径越大，空间电荷的影响就越大，推力器越容易发生电子反流。考虑最严苛的情况，可认为加速栅中心孔的离子束直径保持为0.8倍的加速栅孔径[4]，由此可得加速栅中心孔内的离子束电流为：

（2）放电室等离子体鞘层电势为：

式中：Vd为阳极电压；Vs为屏栅电压。

对于氙离子推力器，下游等离子体电势可由式（10）计算[7]：

式中：Vf为漂浮电势；Ted是下游电子温度，eV。其中，Vf的大小取经验值10 V[8-9]，Ted会随着屏栅电流的增大而升高，根据已有的30 cm氙离子推力器的下游电子温度实际测量值[10]，通过线性拟合可得：

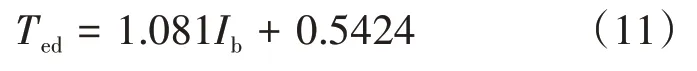
式中：Ib为屏栅电流。

在栅极组件聚焦正常的情况下，靠近加速栅下游表面的孔可能会受到下游产生的电荷交换（Charge-Exchang，CEX）离子造成的溅射刻蚀，因此靠近加速栅下游表面的孔壁刻蚀较为严重，这一结论也与仿真结果相符[11]，因此可以认为轴向距离为ta处的中心电势即为鞍点电势的位置。

（3）在栅极组件的模型中，束流离子的有效加速距离为[4]：

式中：lg为屏栅与加速栅的热态间距；ts为屏栅壁厚度；ds为屏栅孔直径。

由于lg无法实际测量，本文基于J series、NSTAR和LIPS-300离子推力器屏栅-加速栅热态间距最大减小量和放电室功率的数据[12]得到：

式中：Δlgmax为屏栅-加速栅热态间距最大减小量；g(·)表示函数关系；Pd=VdId为放电室功率。

计算时考虑最严苛的情况，即设定屏栅-加速栅的热态间距始终为最大减小量：lg=1-Δlgmax。等离子体电势面到加速栅的距离ld可根据LIPS-300推力器的下游电场环境仿真结果取4 mm[13]。

假定中和器发射的电子能够进入推力器内部时鞍点电势的临界值为0 V[14-15]，电子反流极限电压Vm的性能方程为：

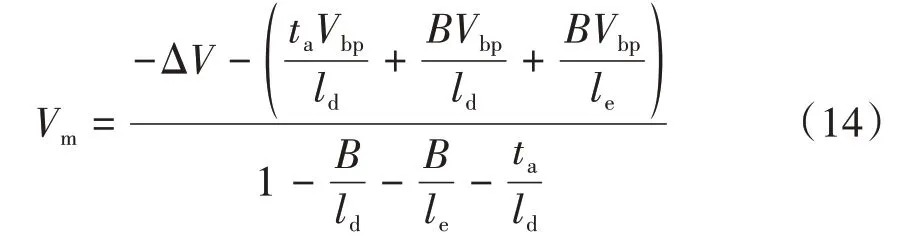
结合式（4）和式（14）可得，推力器的裕量MVm方程为：

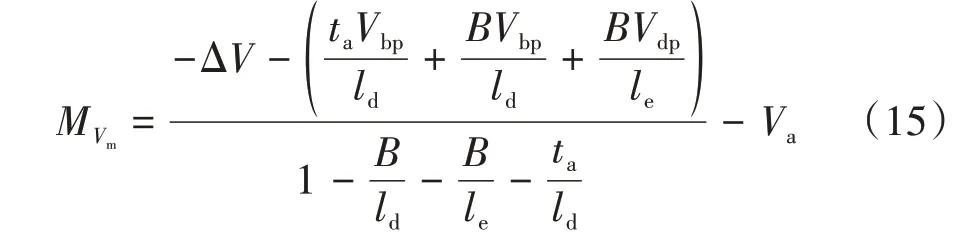
2.2 退化建模

在推力器服役过程中，离子推力器的性能裕量会逐渐随时间退化，必须分析其退化的原因及机制。研究发现，导致性能裕量随时间退化的原因为推力器CEX离子的溅射刻蚀。当CEX离子轰击加速栅孔壁时，宏观上使加速栅孔径增大，孔中心阻止电子反流的势垒变小，从而使推力器发生电子反流失效，推力器工作性能下降，寿命降低，严重时甚至会寿命终结[16]。

加速栅中心孔上游的离子密度最大，因而其附近的CEX离子数量最多，溅射刻蚀也最为严重。因此，针对加速栅中心孔进行退化建模，研究加速栅中心孔的孔径随时间的退化过程。由于加速栅孔刻蚀速率没有可用的实测数据，粒子网格蒙特卡洛碰撞（Particle in Cell-Monte Carlo Collision，PIC-MCC）方法无法脱离仿真而实际统计离子碰撞数，本文利用响应面分析结合仿真试验的方法建立加速栅孔径的退化代理模型。响应面分析是一种拟合输出与输入之间关系的试验设计方法，在响应面分析中，通过设置特定的试验方案，拟合得到响应与影响因素之间的函数关系[17]。通过响应面分析制订试验方案，利用仿真程序得到各参数配置下的响应结果，最终建立加速栅孔径刻蚀速率的代理方程。

在进行响应面分析之前，首先要确定影响加速栅孔壁刻蚀速率的关键影响因素，并明确其在推力器工作时的变化范围。根据这些影响因素对CEX离子的数量、能量或撞击角度是否有显著影响、在离子推力器的实际运行中是否有较为明显的变化以及是否为仿真可控的输入参数的选取原则，最终确定加速栅孔壁刻蚀速率的关键影响因素为屏栅电压Vs、加速栅电压Va、屏栅-加速栅热态间距lg、加速栅中心孔上游离子密度Nm以及加速栅直径da。响应面分析采用Box-Behnken Design（BBD）方法，利用Design-Expert软件进行试验设计。基于选取的关键影响因素及其在推力器服役过程中的变化范围，对各关键影响因素进行归一化处理，并制订试验验证方案，最终利用各参数配置下仿真的加速栅孔壁最大刻蚀速率平均值v̇damax拟合退化方程如下：

进一步对拟合出的退化方程进行误差统计分析，对均方差、可信度、相关系数、调整的相关系数、精确度等参数值进行了计算，如表2所列。

表2 误差统计分析Tab.2 Statistical analysis of errors

多元相关系数R2越大，说明相关性越好；信噪比（Adeq Precision）大于4视为模型合理。通过误差统计分析可以看到，拟合的加速栅孔径退化方程符合上述检验性原则，适应性好。

2.3 可靠性建模

2.3.1 不确定性分析与量化

在退化过程中，推力器的性能裕量会受到各类不确定性的影响，因此在研究确定性性能退化规律的同时，还须对其不确定性进行分析和量化。

（1）不确定性分析

生产制造过程带来的产品个体差异是不确定性的主要来源之一。但是，离子推力器不是批量生产的产品，实际执行任务的离子推力器各项物理属性都是确定的，鉴于此，产品个体差异带来的不确定性不是主要原因，此时的不确定性主要为工作过程中屏栅-加速栅热态栅间距的不确定性和上游离子密度的不确定性。

屏栅-加速栅热态间距lg会随着推力器的启动而变化。由式（13）可知，最严酷情况的热态间距与放电室功率相关。其中，阳极电压保持不变时，热态间距的不确定性转移为阳极电流的不确定性。

此外，由于电离过程中的离子碰撞具有不确定性，栅极组件上游的离子密度也具有不确定性。上游离子密度Nm可由式（17）确定[18]

式中：k为玻耳兹曼常数；Teu为放电室电子温度，K；As为屏栅面积；Ts为屏栅透明度。

考虑放电室电子温度最严酷的情况，并将上游离子密度的不确定性转移为屏栅电流的不确定性。另外，在离子推力器的实际工作中，部分电参数，如屏栅电压、屏栅电流、阳极电流和加速栅电压，会在一定范围内波动。基于以上分析，具有不确定性的参数为Vs、Va、Id、Ib。加速栅直径的不确定性由刻蚀速率的不确定性来表征，同样也可以反映到电参数的不确定性上。

（2）不确定性量化

由上述不确定性分析可知，量化离子推力器的不确定性也就是量化电参数的不确定性。根据设计要求，假设LIPS-300离子推力器电参数均服从正态分布且容差范围为±5%。基于3σ准则[19]，可得到电参数的标准差为：

式中：μele为电参数的均值。

由此可得屏栅电压、加速栅电压、阳极电流和屏栅电流的分布形式为（上波浪线表示考虑了不确定性的参数）：

2.3.2 可靠度度量方程的建立

完成不确定性分析与量化后，结合式（15）和式（16），即可得到推力器的可靠度度量方程：

式中：R为离子推力器的可靠度；P为概率测度；t为推力器的工作时间。

3 试验方案设计

建立可靠性模型后，须通过实际试验对加速栅刻蚀速率模型进行更新，具体是修正栅极刻蚀速率仿真模型来获得更为准确的栅极刻蚀速率数据，以更新加速栅刻蚀退化方程。由于可供试验的样本只有一个，导致试验获得的信息有限，因此为了准确地认知退化规律，确保可靠性与寿命预测的准确性，必须通过试验设计控制试验中的不确定性，保证试验数据的有效性。

3.1 确定试验约束

试验约束条件如表3所列。

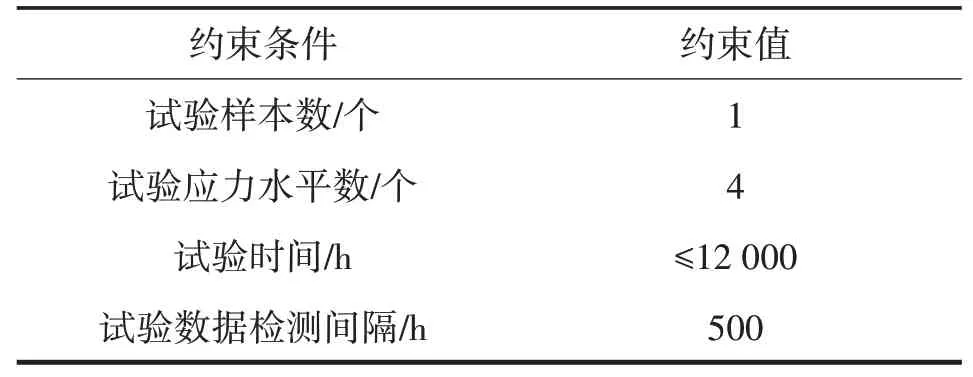
表3 试验约束条件Tab.3 Constraints of test scheme

LIPS-300离子推力器共有23个工况点TL01~TL23，其中TL01~TL02工况不需验证，TL03工况可能会出现在验证任务序列中，验证时长不超过3 000 h。应力水平的选择空间较大，导致直接进行试验设计的计算量较大，因此必须对工况进行初步筛选，最终选取最严苛工况TL23以及不同屏栅电压下对应最大、最小屏栅电流的工况点TL20、TL15、TL14、TL06和TL03对应的应力水平作为备选应力，从中选择试验的4个应力水平，附近的工况点向4个备选应力水平上游合并，即高应力覆盖低应力，这样得到的评估结果更保守。

测试的最短时间间隔为500 h。为了保证在各应力水平下获得足够的信息，每个应力水平应至少测量三次，即每个应力水平对应的最短试验时间为1 500 h。当试验的4个应力水平确定后，各应力水平的试验时长按照总冲分配的原则确定，具体的分配原则为：

设第i（i=1，2…4）个工况点在实际任务时的推力为Fi，总冲为Zi。由于TL23为最严苛的工况，对该工况下推力器的工作情况进行验证是必要的，因此默认TL23工况对应应力为4个应力水平之一，剩下的三个应力水平在TL20、TL15、TL14、TL06和TL03中选择，设试验选择的应力水平从大到小为TL23、TLB、TLC和TLD，其中B、C、D分别代表选定的工况编号。通过是否将TL03工况纳入地面试验考核进行分类讨论。

（1）TLD不为TL03，则有式（21）。

（2）TLD为TL03，则有式（22）。

分配各应力水平的试验时长后，再对试验时长进行调整，使得每个应力水平的时长均为500的倍数且大于1 500 h。

3.2 优化目标

为了保证可靠性与寿命预测的准确性，必须选取合适的优化目标控制试验中的不确定性，保证可靠性模型能够得到正确验证与更新。在本项目的可靠性模型中，退化方程最容易受到试验数据的影响，也是最需要试验验证的，验证并更新退化方程是本次试验的关键目标。

为了更好地验证退化方程并对其进行更新，按照“试验得到的数据点应与理论模型越接近越好”的原则建立优化目标，其中理论模型为不考虑不确定性时LIPS-300离子推力器的退化模型。为了量化考虑不确定性的试验数据点与理论模型的贴合程度，在退化模型中引入模型参数，利用试验数据点对退化模型进行重新拟合，拟合时保留退化模型的原始模型 形式，引入的模型参数an（n=1，2…9）如式（23）：

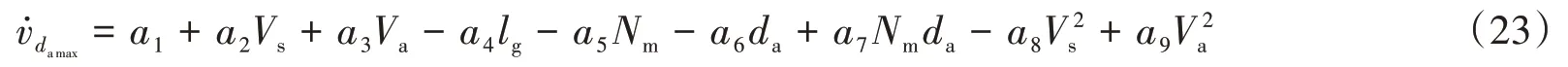
拟合完成后，即可得到新的退化方程：

式中：v̇damax,k为第k个试验方案条件下的加速栅孔直径磨损速率；fk为由第k个试验方案条件下的试验数据点拟合得到的退化方程。

再利用理论模型和拟合模型计算离子推力器实际运行时每个工况结束后的加速栅孔直径增量，并将优化目标设定为由理论模型和拟合模型计算的加速栅孔直径增量的误差平方和：

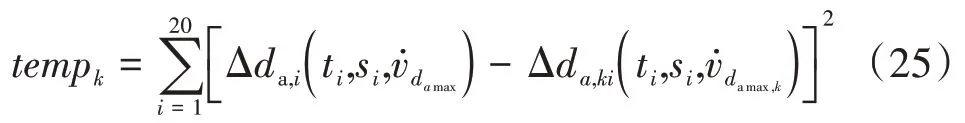
式中：tempk为在第k个试验方案下的拟合模型与理论模型在每个工况结束后计算的加速栅孔直径增量的误差平方和；i为离子推力器实际运行时的工况序号；Δda,i(·)为第i个应力水平下由理论模型计算出的加速栅孔的直径增量；si为第i个应力水平；ti为第i个应力水平的工作时间；Δda,ki(·)为由在第k个试验方案下的拟合模型的第i个应力水平计算出的加速栅孔直径增量。

tempk越小，说明由第k个试验方案得到的试验数据点拟合的退化模型与理论模型越接近，证明该试验方案可以更全面、充分地描述退化规律，能更好地验证退化模型并对其进行更新，得到的可靠性和寿命预测结果置信度更高。

3.3 确定试验方案

基于以上的分析和讨论，本文的试验设计采用的优化目标为：

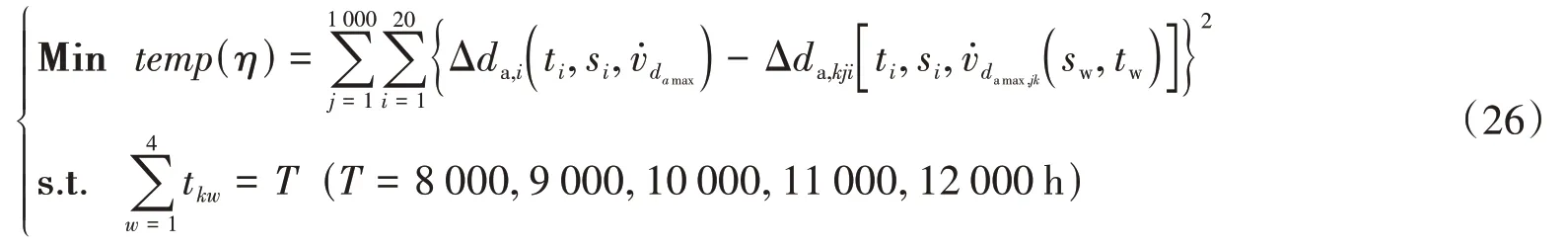
式中：Min和s.t.分别表示目标函数和约束条件；η为试验方案编号；temp(η)为在试验方案确定的情况下，拟合模型与理论模型在每个实际工况结束后的加速栅孔直径增量误差平方和，并将试验重复1 000次得到的误差平方和总和；j为仿真试验次数序号；Δda,kji()·为第k个试验方案条件下由第j次试验的拟合模型在第i个应力水平计算得到的加速栅孔直径增量，tkw为第k个试验方案条件下各工况的试验时长。

参照temp值较小的试验方案，基于实际工程经验，为最严苛工况TL23分配更长的试验时间加以验证，确定了9个试验方案作为备选的最优方案，根据上述优化目标计算各个试验方案的temp，如表4所列。

根据最终的temp结果，表4中序号1的试验方案对应的temp最小，可靠性和寿命预测结果置信度最高。因此，本文将表4中序号为1的方案作为本文选取的最优方案。

为了进一步验证最优试验方案的优越性，选取表4中3个不同temp的试验方案序号1、序号4和序号6进行对比验证，分别计算出对应的加速栅中心孔退化过程的预测结果及电子反流极限电压的预测结果，如表5所列。

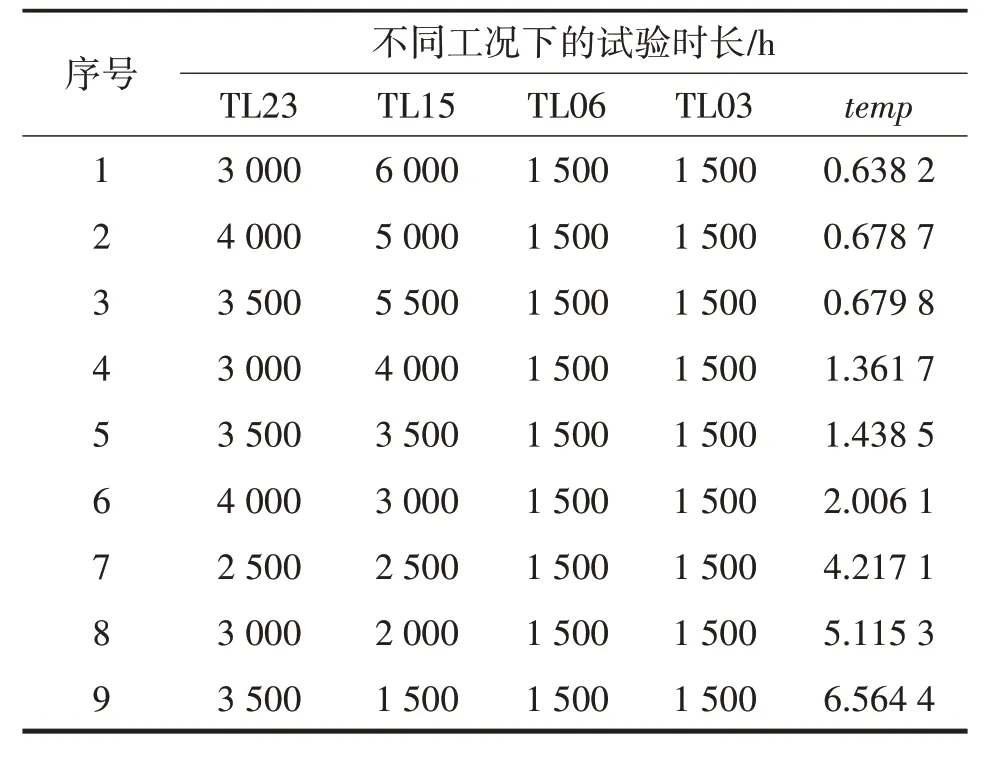
表4 备选试验工况及其时长分配表Tab.4 Alternative test conditions and time allocation

从表5可以看出，试验方案的temp值越小，95%置信度下的预测范围越窄，预测精度越高。此外，理论模型在36 000 h的加速栅中心孔直径为1.684 7 mm，电子反流极限电压为-98.935 6 V，本文选取的试验方案的预测均值与理论模型的实际结果最为接近，预测准确度高。

表5 各试验方案预测结果Tab.5 Prediction results of each test scheme

最终得到的最优试验方案如表6所列。根据试验方案的预测结果，结合式（20）计算，最终完成36 000 h任务的可能性大于0.999 9。

表6 最优工况及其时长Tab.6 Optimal test conditions and time durationcorresponding to the conditions

4 结论与展望

本文基于确信可靠度理论建立了极端小子样、退化不确定情形下的离子推力器可靠性评估模型，并结合任务总冲需求设计了可靠性模型验证试验方案，有效地解决了LIPS-300离子推力器子样数据匮乏、退化过程不确定、1∶1完全试验难实现的问题。为了对LIPS-300离子推力器可靠性评估和试验设计做出更为全面的研究，后续工作可以从以下几个方面展开：

（1）在后续试验基础上，收集相关试验数据，进一步完成可靠性评估的模型验证和校准工作；

（2）针对小行星探测任务需求，更加充分地识别制约离子推力器多模式长寿命的故障机制，从而准确地评估影响长寿命的多种因素及各因素的复杂相关性对推力器可靠性的影响；

（3）尝试建立多工作模式下离子推力器可靠性评估规范，进一步完善评价流程。