不同水沙条件下弯道河床冲淤与漫滩洪水特性研究

王 奇，单钰淇，刘 超*，刘兴年

(1.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2.四川大学 灾后重建与管理学院，四川 成都 610065)

弯曲河道中，水沙运动特性较顺直河道差异显著，河床演变更加复杂[1-2]。部分河流边滩两侧地势险峻、地表风化层厚，物源补给丰富，汛期暴雨频发，洪水陡涨漫滩，洪水与泥沙协同作用，易发生洪沙灾害[3-4]。研究不同水沙条件下弯曲河道河床冲淤规律与漫滩洪水特性有助于揭示弯曲河道水沙灾害形成机制，对减轻弯曲河道洪水灾害有重要意义。

国内外学者对弯曲河道水流运动、泥沙输移及河床冲淤演变展开了大量研究。Blanckaert等[5-6]通过193°急弯水槽试验研究发现，弯道二次环流受弗劳德数Fr影响很小，其强度在较大曲率比（H/R）下饱和且不再随之增大，增加凹岸粗糙度可显著增强弯道中心区域输沙能力。弯道离心力会引起弯道水面由凸岸向凹岸升高，学者们建立了弯道水面横比降和横向超高的计算公式[7-9]。马淼[10]和Li[11]等的数值研究表明，随着弯道弯曲度的增加，弯道水面超高增大，主流更加集中，二次环流逐渐增强。李志威等[12]总结了弯道推移质输移的典型规律，同岸输移大于异岸输移、输沙成带性，形成横向底坡和床沙横向分选。Yen等[13]通过试验发现流量变化越剧烈，弯道泥沙横向分选越显著，凹岸冲深越明显。许栋等[14]研究了流量和弯曲度对连续弯道河床形态的影响，指出流量与床面形态变化呈非线性关系，随着弯曲度增大，床面形态变化更复杂。通过野外观测，Dietrich等[15]发现弯道凸岸浅滩发育促使水流偏向凹岸，影响凹岸及下游河道的河床形态。上述成果揭示了弯曲河道水沙运动特性和河床演变规律，不足的是未考虑来沙条件变化对弯曲河道水沙运动与河床演变的影响。

以往学者主要采用原型观测、水槽试验和解析模型研究弯曲漫滩河道水沙运动和滩槽演变。Constantine等[16]考察亚马逊流域发现，泥沙补给加快了弯曲河道的横向迁移速率，促进了河漫滩地形的重塑。Harrison等[17]结合原型观测和数学建模发现，河漫滩地形受洪水大小、河道曲率、滩地床沙性质、河岸植被阻力等因素控制。相比未漫滩弯道，漫滩弯道中二次环流结构更复杂，离心力和滩槽水流交换共同影响二次环流[18-19]。洪水漫滩后，相对水流未漫滩时，主河道水流流速降低、推移质输沙率减小；随着漫滩水深增加，推移质输沙率逐渐增大[20]。蔡金德等[21]采用概化模型探讨了连续弯道滩槽演变规律，认为过渡段长宽比接近3时，可提高枯水期过渡段浅滩冲沙能力，有利于维持通航水深。基于水流连续方程和动量方程，Liu等[22-23]提出了弯曲漫滩河道水流流速空间分布计算模型。上述成果揭示了弯曲河道中漫滩洪水各项特性并提出了计算方法，但欠缺不同来沙条件下弯曲漫滩河道冲淤演变、洪水位变化等方面的深入研究。

水沙条件变化是驱动弯曲河道河床演变的主要原因之一[24]。水流与来沙条件变化改变河道原有泥沙输移过程，促使河道发生冲淤演变。近年来，长江上游梯级水库陆续建成投运，三峡水库下游泥沙补给大幅减少，改变了坝下游部分弯曲河道河床演变规律，弯曲河道河床由“凸淤凹冲”转变为“凸冲凹淤”[25-26]。另外，弯曲河流中，水沙条件突变可能加剧洪水灾害。王协康等[3]指出排洪输沙能力较弱的弯曲河道为山洪易灾区，主要表现为超量泥沙补给下河道淤堵、洪水水位陡增致灾。基于上述分析，本文通过水槽试验，揭示不同水沙条件下弯曲河道河床演变规律与漫滩洪水特性。

1 水槽试验布置

概化模型试验在90°弯曲河道中进行，水槽布置见图1所示。

图1 弯曲水槽布置Fig. 1 Layout of the curved flume

河道由主槽和边滩组成，主槽宽B1=0.3 m，深0.3 m，距槽首2.5 m处往下游方向主槽凹岸为边滩，宽B2=0.5 m。主槽和边滩横向水平，床面纵向比降为S=1%。弯道主槽轴线半径r0=1.2 m，中心角θ=90°，径宽比r0/B1=4。弯道进出口分别与长3 m和1 m的顺直段连接。主槽铺有中值粒径d50=2 mm的非均匀天然沙，其级配曲线见图2，河床坡降为1%，滩地及直立边壁用水泥浆抹面。水槽末端设置与铺沙厚度等高的挡板控制侵蚀基准面，尾部接沙框可收集主槽输移的推移质泥沙，采用电磁流量计测量流量。本文试验不考虑河道内桥梁、涵洞等涉水建筑物对水沙输移的影响。

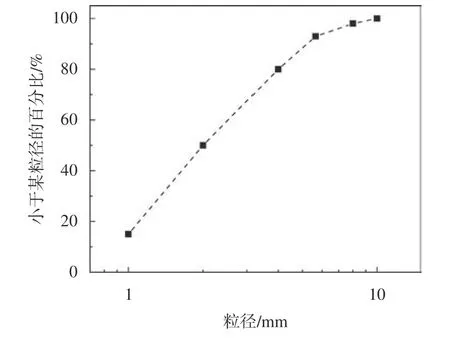
图2 试验沙级配Fig. 2 Particle size of bed material

本文设计了A、B和C共3个系列试验，试验参数详见表1。对于A、B两组试验，河床冲淤稳定后，用测针分别测量弯道凹凸岸水位及河床高程、上游顺直段水位及河床高程。90°弯道每间隔10°设置1个测量断面，在凹岸、凸岸附近各选取1个测点测量水位，每个点测3次。停水晾干后，测量弯道各断面河床高程，各断面选取6～10个测点。测量水槽上游顺直段距槽首1.0、1.5和2.0 m处3个断面的水位及停水后的河床高程，每个断面选取5个测点，每个测点测3次。C组试验除了不测弯道各断面凹凸岸水位，其余测量内容与A、B组试验一致。另外，采用LGY-Ⅱ型智能流速仪测量C组主槽中心线和弯道边滩水流流速纵向分布，测点布置如图1中“×”所示。

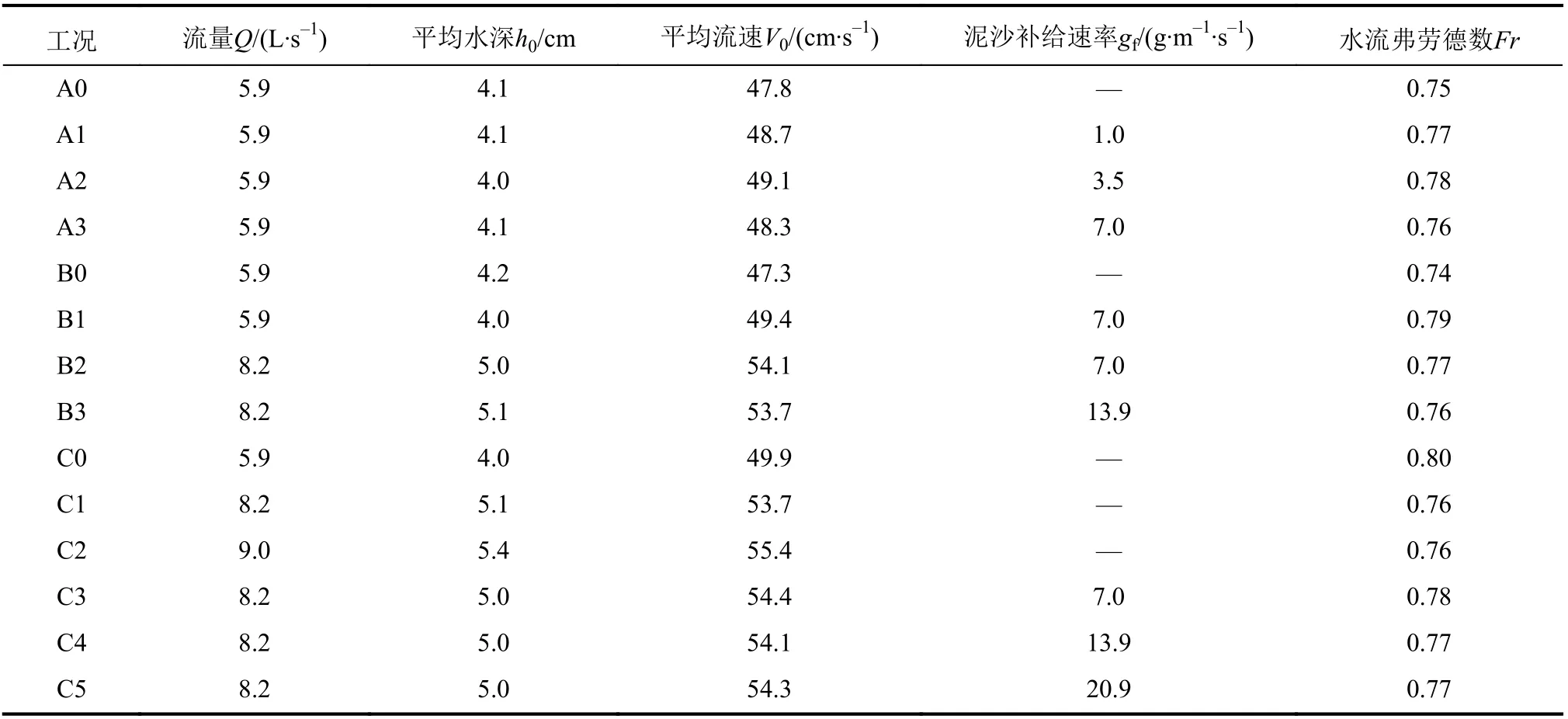
表1 各工况试验参数Tab. 1 Experimental parameters

弯曲水槽模型试验步骤如下：首先，将床沙搅拌均匀，按照预设基准线铺于主槽，释放小流量使床沙密实，之后，缓慢增大流量至设计值开始试验。A组试验铺沙厚度为14.0 cm，各工况水流均不漫滩。B组和C组试验铺沙厚度为16.5 cm，每个工况水流均漫滩。每组试验第1个工况为清水冲刷，当推移质输沙率小于0.2 g/(m·s)时[27]，认为主槽河床已形成稳定粗化层，随后在粗化层上开展不同水沙条件下河道演变试验。A组试验流量不变，泥沙补给量依次增大。工况A1～A3的加沙率分别设定为小于、3倍和6倍的弯曲主槽平衡输沙率。在流量5.9 L/s下，主槽平衡输沙率由预试验测定，当上游加沙量与下游接沙量一致时，得到gt(0)=1.2 g/(m·s)。工况B1与B0流量相同，来沙量为6倍主槽平衡输沙率；工况B2、B3流量增大，上游来沙依次为6倍和12倍的主槽平衡输沙率。工况C0～C2为流量逐渐增大的清水冲刷河床粗化试验，水流均漫滩。在工况C2冲刷形成的河床粗化层上继续开展工况C3～C5，工况C3～C5流量相同，泥沙补给分别为主槽平衡输沙率的6、12和18倍。在工况C3～C5加沙进行1和2 h及河床冲淤稳定后，分别测量主槽中心线和边滩各测点的水流纵向流速。对于加沙工况，加沙时间为3 h，距槽首1 m处每20～30 min加一次沙，补给泥沙与床沙级配相同。所有工况每隔1 h收集1次主槽接沙框内的泥沙，将其晾干、称重，得到每小时推移质输沙量。各工况水流流态均为缓流，上游顺直河段水流近似为恒定均匀流。

2 试验结果

2.1 不同水沙条件下弯道水面超高

水流由顺直段进入弯曲段后，水体受离心力作用，弯道水面出现横比降，凹岸水位高于凸岸水位，其水位差称为水面超高。本文讨论弯道水面横向超高沿程最大值ΔH，其通常出现在弯道环流充分发展区，一般在弯顶断面以下[8]。

图3给出了弯道最大水面超高与流量和泥沙补给的变化关系。

图3 最大水面超高与流量和泥沙补给速率的变化关系Fig. 3 Water surface superelevation versus flow discharge and sediment supply rate

由图3（a）可知：流量越大，弯道水面超高越大；然而在相同流量下，不论水流是否漫滩，弯道水面超高并不相等，这表明除流量外，来沙变化也影响弯道水面超高。从图3（b）可知，弯道水面超高随泥沙补给增加而增大，因为泥沙补给造成河床淤积抬升，进而影响弯道水面超高。

由于河床演变影响弯道水面超高，如何对其进行准确预测是一个难点。以往弯道水面超高计算公式大多基于弯道水流受力分析推导得出，表示如下：

基于工况A0～A3和B0～B3的水面超高ΔH实测数据，图4对比了兰运长公式[7]、张红武公式[8]和毛佩郁公式[9]对水面超高ΔH的计算值。结果发现，兰运长公式[7]计算结果最佳（平均相对误差小于5%），其余两个公式计算值均较实测值偏低。这是因为：兰运长公式中的经验系数a0利用大量原型和模型资料率定得到，包含了流速分布不均与河床演变对水面超高的影响[7]；张红武公式未充分考虑水深沿河宽的变化及流速分布不均对水面超高的影响，故计算结果相对较差[8]；毛佩郁公式中的a0值仅依据少量物理模型数据，适用范围有限[9]。天然弯曲河流几何形态不规则、弯道河床形态有差异，需更多原型和试验资料，针对不同特征的弯曲河道率定经验参数，提高水面超高计算精度。

图4 水面超高的公式计算值与实测值对比Fig. 4 Comparison between predicted and measured water surface superelevation

2.2 不同来沙条件下未漫滩弯道河床演变

图5给出了恒定流量不同来沙条件上游顺直河段的河床冲淤变化，河床高程值为相对初始铺沙河床的地形变化值，正值表示淤积，负值表示冲刷，下同。由图5可知：随着工况A0～A3泥沙补给逐渐增大，上游顺直段河床冲刷深度明显减小、河床淤高。以工况A1为例，上游顺直段泥沙补给速率为1 g/(m·s)，泥沙补给总量约3.2×103g。与工况A0相比，工况A1上游顺直段淤积泥沙为1.2×103g，约占补给泥沙量的38%；被水流输运至槽尾的泥沙为1.3×103g，占泥沙补给量的40%；弯曲河段有少量淤积，淤积量约为0.5×103g，约占泥沙补给量的16%。类似地，工况A2与A3中分别有35%和25%的补给泥沙沉积在上游直段，主槽泥沙输移量分别占补给泥沙的39%和42%，仅约10%的补给泥沙淤积在弯曲河段。少量补给泥沙沉积在弯道段，对弯道段河床演变的影响有限。

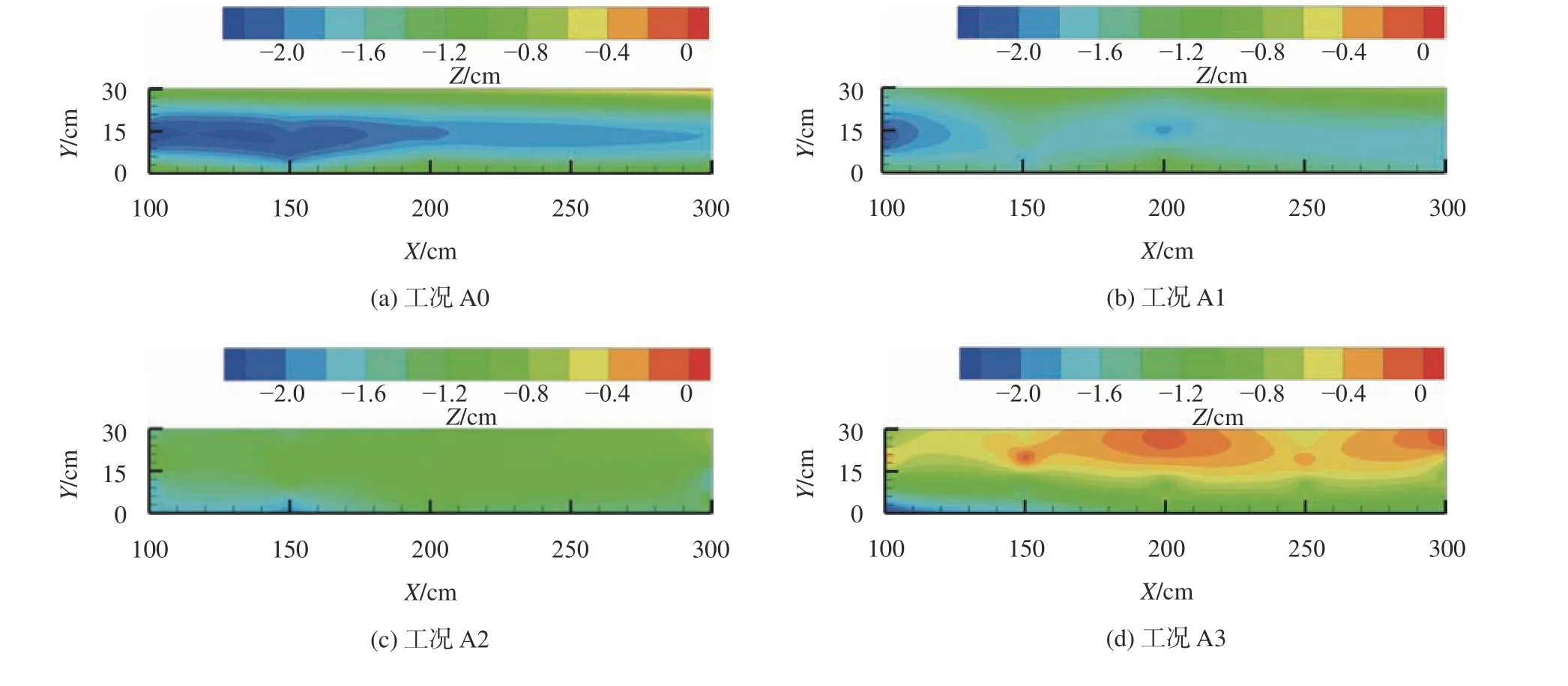
图5 工况A0～A3上游顺直河段河床冲淤变化Fig. 5 Bed topography of upstream straight reach in case A0～A3

图6给出了恒定流量不同来沙条件未漫滩弯曲河道的河床冲淤变化。由图6可知：当泥沙补给小于河道输沙能力时（工况A0和A1，对应图6（a）和6（b）），弯道河床高程变化很小，这是因为少沙条件下河床表层粗化层相对稳定。随着泥沙补给量增大，工况A1～A3的弯道凹岸区域冲刷深度几乎相同，而凸岸淤积高度和范围随泥沙补给增加而小幅增大（图6（b）～（d））。具体来讲，随着泥沙补给从1 g/(m·s)增加至7 g/(m·s)，凸岸淤积高度仅由2.7 cm增大为3.4 cm。这是因为大部分泥沙淤积在上游顺直河段或被输运至水槽末端，仅有少量泥沙（10%～16%）沉积在弯曲河段。因此，即使泥沙补给量增大为弯道平衡输沙量的6倍，弯道河床整体冲淤变化不大。

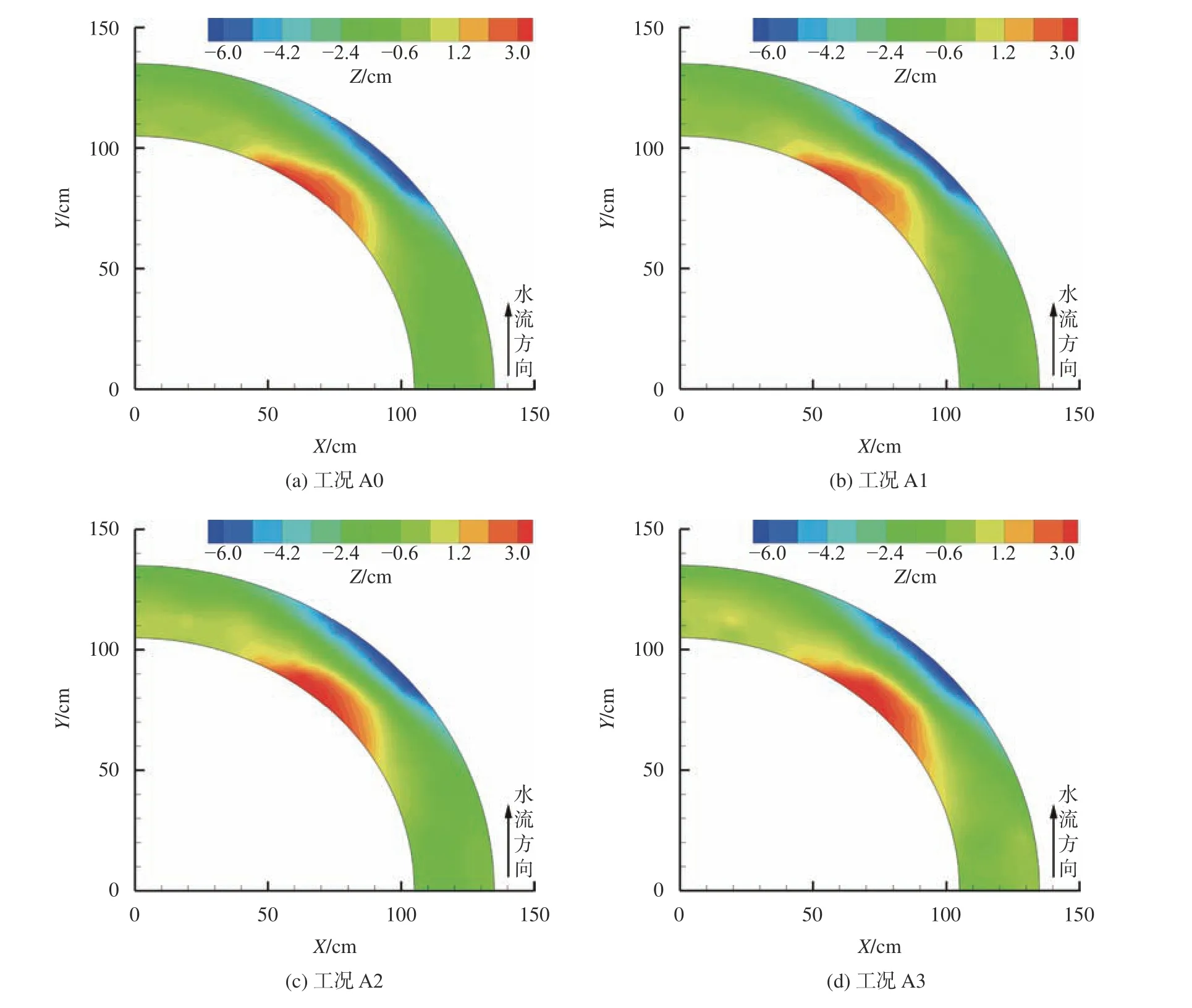
图6 工况A0～A3未漫滩弯曲河道河床冲淤变化Fig. 6 Bed topography of meandering channel with bankfull flows in case A0～A3

不同泥沙补给下，弯曲河道水位沿程变化不明显。图7给出了工况A0～A3弯道凹岸水位的沿程变化，随着泥沙补给速率增加，工况A0～A3凹岸水位并未发生显著变化，工况A3（绿色线）较工况A1的水位上升不到水深的10%。相似地，凸岸水位也未发生显著变化。因此，对于弯曲未漫滩河道，上游泥沙补给变化虽影响凸岸河床淤积，但对弯道段水位提升影响不大。

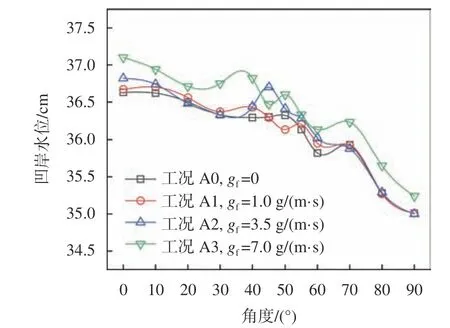
图7 工况A0～A3弯道凹岸水位沿程变化Fig. 7 Water surface elevation along the outer bank of the channel bend in case A0～A3

2.3 不同水沙条件下漫滩弯道河床演变

相比A组试验，B组试验铺沙厚度更厚，河床基准面变高，以使工况B0流量刚好漫滩。在工况B0形成的河床粗化层上开展工况B1～B3（流量、泥沙补给量均增大）探究弯曲段河床形态及水位变化。

图8给出了工况B0～B3上游顺直段河床冲淤变化。由图8可知：相比工况B0，工况B1流量不变，泥沙补给为6倍弯道平衡输沙率，顺直段泥沙淤积导致河床高程稍有增加。相对工况B1，工况B2和B3增大流量和泥沙补给后，上游顺直段河床先冲刷后保持稳定（图8（b）～（d）），河床冲淤程度最终与工况B0相同。计算可知，工况B1～B3中，上游顺直段河床淤积量分别为5.2×103、5.9×103、1.3×103g，占补给泥沙的23%、26%、3%；弯道河床淤积量约2.0×103、3.0×103、1.8×103g，占补给泥沙的9%、13%、4%。这表明B1～B3工况中，大部分（61%～93%）补给泥沙经弯道输运至下游。

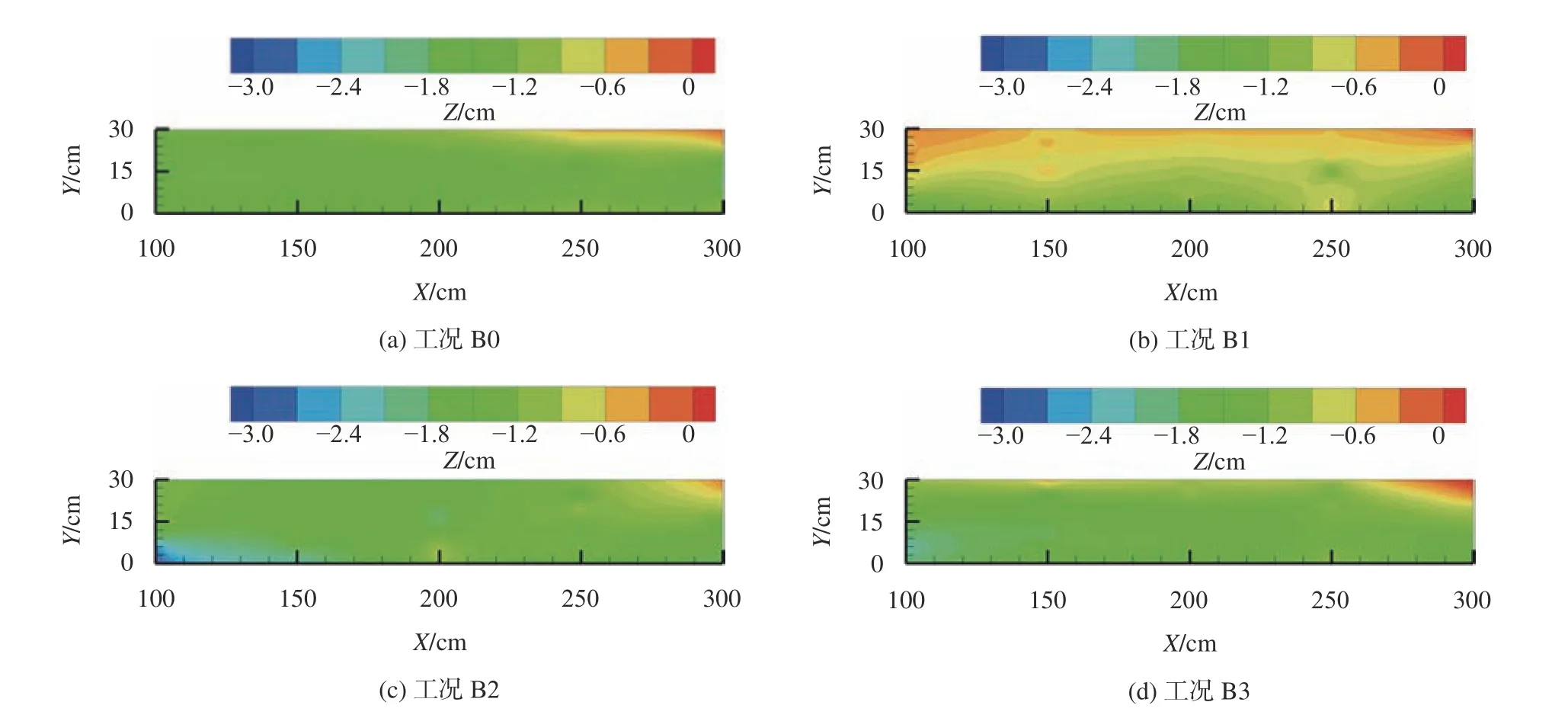
图8 工况B0～B3上游顺直河段河床冲淤变化Fig. 8 Bed topography of upstream straight reach in case B0～B3

图9给出了漫滩洪水下弯曲河道主槽的河床冲淤变化。由图9可知，工况B1与B0比较，弯道河床高程整体略微抬高，但变化不明显。工况B2泥沙补给不变、流量增大，除了凸岸中心断面淤积高度降低，河床高程整体均升高，表现为凹岸冲坑范围减小，弯道下半段淤积增加。这是因为水流强度增大将上游补给泥沙冲向下游弯道，水流漫滩后弯道输沙能力降低[20]，导致推移质泥沙淤积。随着来沙量增大（泥沙补速率为工况B2的2倍），工况B3弯道河床高程相比工况B0整体抬升约45%。

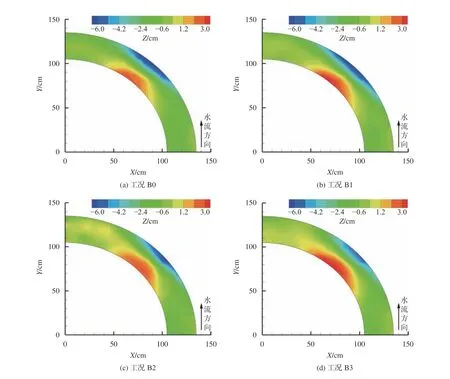
图9 工况B0～B3漫滩弯曲河道主槽冲淤变化Fig. 9 Bed topography of main channel in bend with overbank flows in case B0～B3

图10给出了水流漫滩工况B0～B3弯道凹岸水位的沿程变化。 由图10可知，工况B2与B3增大流量后，凹岸水位明显增加，相比工况B0、B1，工况B2和B3水位上涨约30%。然而，泥沙补给增大并未对沿程水位产生明显影响。例如，工况B2与B3的流量相同，泥沙补给分别为7 g/(m·s)和13.9 g/(m·s)，但两工况沿程水位变化几乎相同。

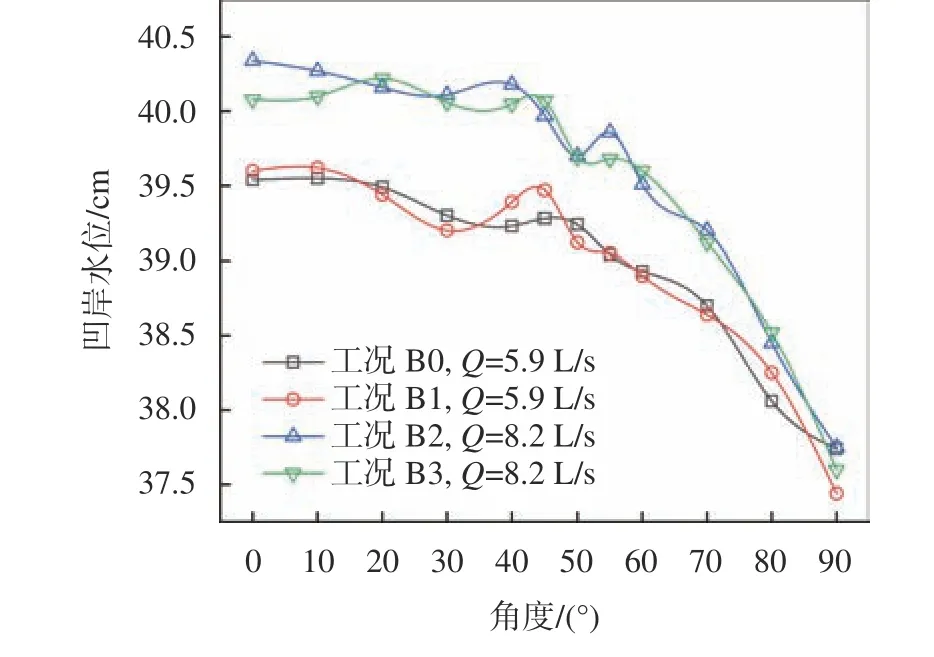
图10 工况B0～B3弯道凹岸水位沿程变化Fig. 10 Water surface elevation along the outer bank of the channel bend in case B0～B3

综上，对于弯曲漫滩河道，上游泥沙补给对河床淤积、水位提升均有影响，但流量增大是弯曲河道漫滩洪水水位升高的主要原因。

2.4 弯道漫滩洪水流速沿程分布

A、B 2组系列试验研究了弯道上游不同水沙条件对弯道河床演变、水位抬升的影响。C组试验铺沙厚度与B组一致，各工况水流均漫滩，重点关注不同水沙条件下，弯曲河道主槽和滩地流速沿程分布。C组各工况与B组各工况的流量和泥沙补给量相似，因此，C组各工况河床演变特征与B组极为相似，这里不再赘述。图11为C组各工况滩槽水流流速的沿程分布，横坐标表示到原点的距离及对应弯道断面的角度，即以弯道0°断面为原点所在断面，平行于顺直河段指向下游为横轴X正方向，将弯道各流速测点对应弧长拉直作为X轴上的横坐标值，横坐标上方标明各测点所在断面的弯道角度。

试验过程中，不同时刻（加沙1、2 h及河床稳定后）河道流速数值和变化趋势十分接近，表明河床冲淤变化对水流流速影响较小，此处选用河床稳定后的测量流速开展分析。由图11可知，图11（a）和（b）分别表示不同来流条件（工况C0～C2）和不同来沙条件下（工况C3～C5）主槽中心及弯道边滩的水流流速沿程分布，其中MC代表主槽，FP代表凹岸滩地。分析图11可知，不同工况中，主槽水流纵向流速沿程变化遵循同样的规律：上游顺直段流速基本不变；水流进入弯道后，流速随角度增加先减小后增大，在50°断面附近达到最小值（约为0.6倍上游流速），在弯道出口处恢复至上游流速。由于弯道边滩分流作用，边滩水流流速沿程先增大后减小，在50°断面达到峰值，流速峰值超过上游来流流速（约为1.3倍上游流速）。需注意，在30°～60°断面，弯道边滩水流流速大于弯道主槽和上游来流流速。这表明弯曲河段30°～60°区域边滩漫滩水流流速较上游来流更大，可能造成滩地洪水灾害。

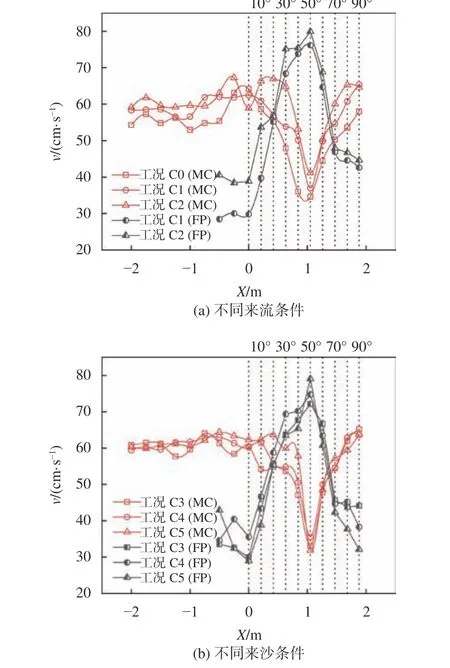
图11 主槽中心线及凹岸滩地纵向流速分布Fig. 11 Longitudinal velocities along the centerline of the main channel and the floodplain

综上，上游来流量是弯道河床地形演变、水位变化和滩地流速变化的关键，而泥沙补给对弯道河床冲淤演变的影响相对较小。洪水漫滩后，90°弯曲河段中断面（30°～60°）附近边滩水流流速增大。

3 结 论

不同水沙条件下，对比前人公式对弯曲河道水面横向超高最大值的计算结果，发现兰运长公式能较好预测河床冲淤稳定后的弯曲河道水面横向超高最大值。

水流不漫滩时，上游泥沙补给对弯道河床地形和水位影响均较小。流量不变，增大泥沙补给仅造成弯道凸岸少量淤积。

洪水漫滩时，上游来流量是影响弯道水位和滩地流速的主要因素，上游泥沙补给是次要因素。流量增大造成弯道沿程水位明显抬升。洪水漫滩后，90°弯道凹岸中断面（30°～60°）附近边滩水流流速显著增大，最大值出现在50°弯道断面，约为上游平均来流流速的1.3倍。