考虑激励相容的含风电电力市场价格机制研究＊

郝如海，包广清，周治伊，冯文涛，郝培良

（1.国网甘肃省电力公司电力科学研究院，甘肃 兰州 730070；2.兰州理工大学电气工程与信息工程学院，甘肃 兰州 730050）

1 引言

随着风电渗透率的大幅提高，增加了系统供需平衡压力，需要通过市场机制设计充分挖掘系统灵活调节潜力，保障电力电量平衡。因此，在经济性、可靠性以及价格体系之间取得最优权衡是一个至关重要的问题。价格机制在电力市场的建设中发挥着重要的作用，目前发展较为完善的电力市场，如美国PJM电力市场、得克萨斯州、加利福尼亚州、纽约州，以及英格兰地区为代表的电力市场，主要采用节点边际电价机制（Locational Marginal Pricing，LMP）进行日前市场出清[1]。在首批8个电力现货试点中，广东、甘肃等电力日前市场也采用LMP电价机制。在该机制下，发电商参与电力市场，向系统运营商（Ind-ependent System Operator，ISO）申报成本，由ISO建立日前市场模型，对日前市场出清并生成LMP[2-3]。

对于采用LMP机制进行日前出清的电力市场，只有在市场完全竞争的假设下，才可以促使发电商真实报价，实现系统总成本最小化[4]。从博弈论的观点来看，电力市场交易属于不完全信息动态博弈，发电机组作为理性个体，其目的是通过参与市场使自身获利最大化[5]。因此，发电商有动机向市场运营商提供不同于其真实边际成本的价格，以此改变市场出清价格，谋求自身利益。文献[6]证明发电商可以通过保留容量或提高边际成本来提高电价，这种策略行为可能会导致资源错配，降低市场效率。为解决LMP机制的这种缺陷，迫切需要对满足激励相容准则、促进市场成员提交真实成本的电力市场电价机制进行研究。

在现有市场机制设计理论中，Vickrey-Clarke-Groves（VCG）是一种激励市场成员申报真实信息的出清方式[7]。在VCG机制下，每个市场成员获得的支付取决于给市场带来的经济价值，已经在电力市场机制设计中得到了初步应用。针对常规发电商，文献[8]提出了电力市场VCG竞争机制，根据其市场贡献度进行价值分配和价格结算。文献[9]应用风电聚合商对风电机组进行利益结算，通过VCG机制激励风电机组申报真实的发电概率分布函数，从而获得最大市场盈余。文献[10]证明了在输电线路无拥塞时，VCG节点平均电价始终高于LMP，但在日前市场出清建模过程中未考虑风电机组的渗透率因素。文献[11]提出含风电竞标的日前市场VCG出清电价机制，激励发电机组申报真实发电成本及风电功率概率分布函数，然而该VCG价格机制存在收支不平衡问题。

综上，虽然VCG机制可以激励发电商真实报价，保证各区域的自治性，但是关于风电渗透率对日前市场出清电价的影响以及收支平衡等问题尚缺乏深入研究，因此本研究提出了基于资金再分配策略的改进VCG（Improved VCG，IVCG）。首先，建立考虑风电不确定性的日前市场出清模型；其次，基于VCG机制设计理论，定义发电机组获得的支付为该机组参与日前市场出清前后总成本的变化量，对该机制需要满足的激励相容、个体理性以及系统成本最小化等特性进行理论证明，并通过不同风电渗透率场景分析，建立一种可以实现系统收支平衡的市场分配策略；最后，以IEEE 24节点为例验证了该日前市场出清电价机制的有效性。

2 日前市场出清机制

2.1 日前市场出清模型

建立日前市场出清模型之前先做如下假设：（1）假设线路无拥塞且常规能源的生产成本函数为线性函数；（2）不考虑沉没成本，由于风电的可变运行成本低，风电的生产成本近似为零；（3）采用直流潮流模型出清日前市场，不考虑无功功率及其网损；（4）各节点电力负荷刚性；（5）发电商的策略行为不受风力发电量影响。

考虑风电出力的随机波动性，本研究根据不同发电场景对日内市场的运行情况进行预测，并建立两阶段随机规划模型实现日前市场出清，目标函数为最小化日前总发电成本与日内期望调整成本。

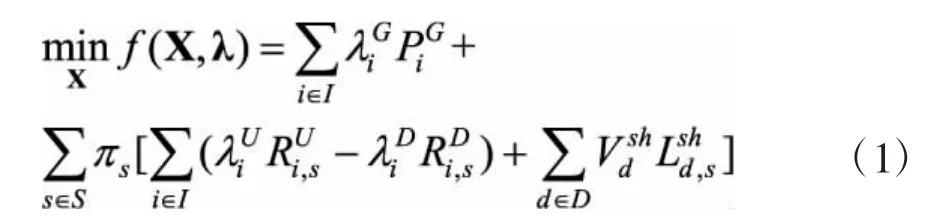
式中：决策变量用向量X表示，可分为与场景独立的日前决策变量XDA和与场景相关的日内决策变量XRT。日前决策变量XDA包含常规发电机组i的出力，风电机组l的出力和节点n处的电压角δnDA。日内决策变量XRT则由常规发电机组i向上/下调整功率/，系统对负载d的切负荷功率，风电机组l的弃风功率以及节点n处的电压角组成。λ为常规发电机组申报的成本，包含发电成本λiG以及向上/下功率调整成本λiU/λiD。表示系统运营过程中切负荷成本。约束条件：

1）功率平衡约束

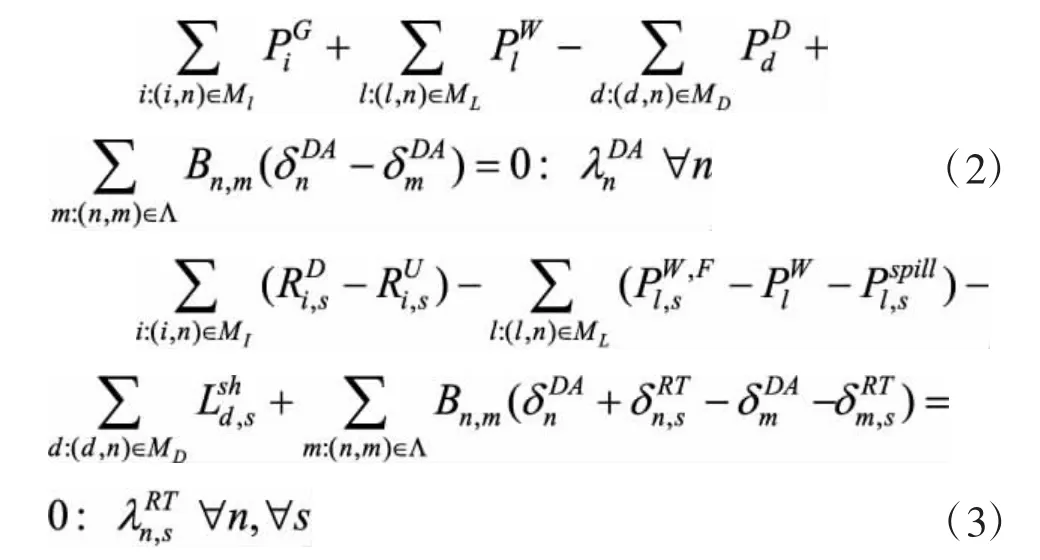
（2）式为日前市场各节点功率平衡约束，（3）式表示日内市场各节点功率平衡约束。式中：M1，ML，MD为常规机组、风电机组、需求集合向系统节点集合的映射，A表示输电线路集合。为场景s下风电机组l的实际发电量。Bn，m为节点n，m之间线路的导纳。和分别表示（2）式和（3）式的对偶乘子。

2）输电线路功率约束

为防止输电线路超载，需要满足线路有功潮流约束。

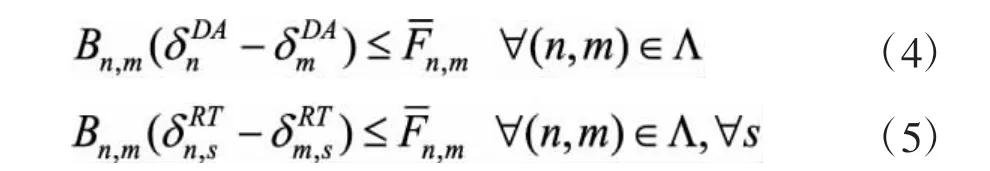
3）常规机组出力约束

4）风电机组出力约束

在日内市场，受风电出力不确定性的影响，调度中心首先通过调用常规发电机组的备用功率保证系统安全可靠运行。当常规发电机组预留的备用功率无法保证输电网络安全运行时，即：

5）常规机组上/下调备用功率约束

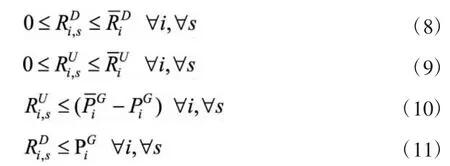
6）风电机组弃风功率约束

7）系统切负荷约束

上述约束条件中式（2）、（4）、（6）和（7）与日前市场出清阶段相关，式（5）、（8）、（9）、（12）和式（13）包含与日内市场出清相关的决策变量，而其余约束条件关联了日前出清与实时出清两个阶段。因此，上述考虑日内场景的日前市场出清模型是一个两阶段随机规划问题。通过YALMIP[12]调用CPLEX[13]优化求解上述模型，即可得到常规机组最佳发电量及储备量，以及风电机组的日前市场出力计划。

2.2 节点边际价格机制（LMP）

节点边际电价机制LMP表示负荷增加一个单位时电网运行成本的增量，等于系统节点负荷平衡约束的对偶乘子[14]，在日前市场中，节点n的边际电价λnLMP为：

处于同一节点的发电机组以相同的价格进行结算。系统运营商在日前市场中支付给常规发电机组i及风电机组的费用分别为：

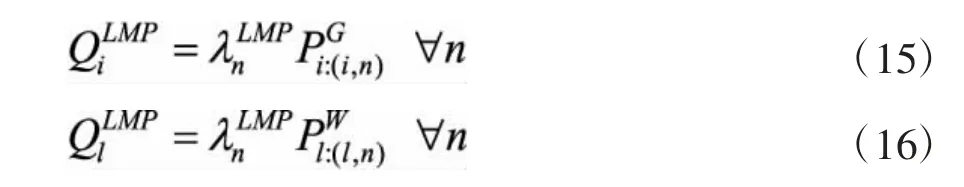
在完全竞争的电力市场中，市场出清电价对于市场参与者而言是参数而非变量，LMP机制能够保证系统总成本最小。然而，实际电力市场难以达到完全竞争的状态，发电商为谋求自身利益，通过策略性报价改变出清价格，提高自身收益，降低市场效率，无法实现系统成本最小化。

3 VCG机制设计

为激励各发电商申报真实成本，实现系统总成本最小化，本研究基于VCG理论，提出适应高比例风能参与的日前市场价格机制设计。

3.1 设计目标

机制设计理论提出了相关标准化的性质与条件，用于分析价格机制的优劣。本研究重点关注系统成本最小化（Cost Minimization，CM）、个体理性（Individual Rationality，IR）、激励相容（Incentive Compatibility，IC）以及收支平衡（Budget Balance，BB）。

3.1.1 成本最优

在电力市场框架下，系统成本最优是指各常规机组与风电机组按照日前市场出清模型求解得到出力计划时，能够达到各自真实成本最小化目标。

当所有常规机组按真实发电成本向市场运营商申报时，在日前市场出清模型中，系统总成本最小化的性质自动成立。若存在常规机组向系统运营商提供策略性报价时，则导致系统常规机组和风电机组的出力计划难以实现市场出清总成本最小化。

3.1.2 个体理性

个体理性是市场成员通过参与市场来获得激励，即参与市场的行为是出于自愿的[15]，这也是市场成员的参与约束。在电力市场框架下，即确保发电商参与市场的利润不为负。

3.1.3 激励相容

每个参与者都能根据自己的真实偏好来实现机制目标，那么这种机制被称为激励相容机制。在电力市场中，当参与市场的所有发电商均真实申报发电成本时，能够实现自我利益最大化，则该价格机制满足激励相容。

3.1.4 收支平衡

收支平衡表示系统运营商从负荷侧征收的费用与向发电侧支付的金额相同。

3.2 设计方案

在LMP机制下，日前市场出清价格等于系统节点负荷功率平衡约束条件的对偶变量，这对同一传输节点内的所有参与者均相同。VCG机制则根据每一位生产者为市场做出的贡献来进行支付，位于同一节点的任意两个市场参与者所获得的系统支付价格可能不同，因此VCG机制能够有效区分位于同一节点的两个生产者的生产价值。例如，假设某节点存在A与B两个发电商，仅发电商A具有预留的灵活性容量。在电力市场日前出清计划中，发电商仅根据其电能产量获得报酬。虽然发电商A和B都可以生产同质同量的电能，但在风电日内实际出力与日前计划出现偏差时，缺少发电商A可能会导致电力系统出现切负荷或弃风的情况。因此，发电商A应比发电商B获得更多的支付，而在LMP价格机制中，发电商A的价值并未在电价上得到体现。在VCG价格机制下，常规发电商的价值可以对应获得的支付QJVCG为：

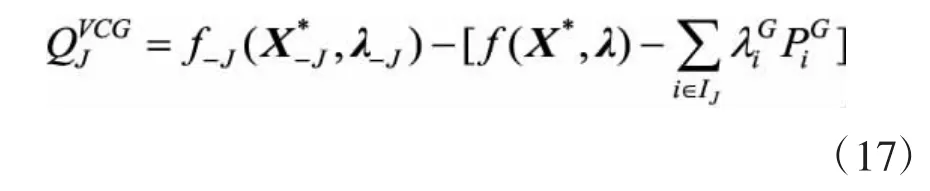
式中：f-J（·）表示常规发电商J不参与市场时的系统成本函数，X*-J为J不参与市场时其他发电商的最优调度计划，X*是所有发电商参与市场时，系统最优调度计划。IJ是J常规发电机组集合。因此，第一项f-J（X*-J，λ-J）表示发电商J不参与市场时，其他发电商的总成本。第二项f（X*，λ）-表示J参与市场时，其他发电商的总成本，即系统J总成本减去常规发电商J的成本。

同理可得，对于风力发电商K，其获得的支付为：

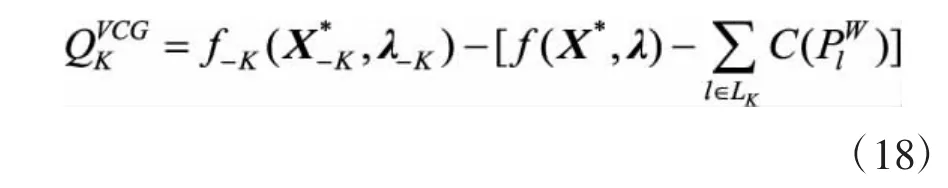
本研究基于VCG理论的电价机制设计具有典型的经济学意义，从而实现市场成员个体利益最大化与市场出清总成本最小化的一致性。

3.3 性质证明

已有研究验证LMP机制可以实现个体理性和收支平衡性质，但对于激励相容以及系统总成本最小化的性质，无法始终满足。通过证明本研究机制满足激励相容、个体理性以及系统成本最小化性质，提出一种新的不平衡资金分配策略，以满足收支平衡。

3.3.1 激励相容

对于常规发电商，在VCG机制下的收益来自系统运营商的支付。由式（17）可知，J为追求自身利益，向系统运营商提供优化后的策略报价，而非其真实发电成本。为确保J的最优报价，其目标函数为：

此时J净利润实现最大化，即从系统运营商处获得的收益与其发电成本的差额最大。

将式（17）带入式（19）中可得：

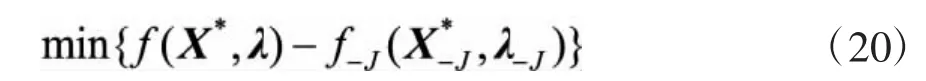
在式（20）中，第二项f-J（X*-J，λ-J）表示常规发电商J不参与市场时，其他发电商的总成本，即非常规法电商总成本可与发电商J的决策相互独立。此时，目标函数只剩第一项f（X*，λ）即所有生产商参与电力市场时系统的发电总成本。因此，系统总发电成本最小化目标与常规发电商J的优化目标，其占优策略必然是向系统运营商提供真实发电成本，该行为会使系统总发电成本最小。同理可得，对于风电商而言，提供真实发电成本是其占优策略。

由此看出，基于VCG机制的价格结算方式能够消除发电商利用市场力量虚报发电成本的能力，满足激励相容。

3.3.2 个体理性

上节证明了基于VCG理论的价格结算机制满足占优策略激励相容，因此，所有发电机组将向系统运营商申报真实发电成本。同样以常规发电商为例，根据式（17）和式（19）可得，常规发电商J的净利润为发电商J不参与市场时，其他发电商的成本之和，减去所有发电商参与时的系统总发电成本。f-J（X*-J，λ-J）等效于在所有机组参与的日前市场出清过程中，将属于发电商J的常规发电机功率均置为0，即在出清模型中增加约束条件。因此，出清模型优化可行域缩小，目标函数值不小于所有发电商参与出清计划时的目标函数值。即

同理可以得出风电商在该价格机制下参与市场时，满足个体理性。

3.3.3 成本最小化

由上述证明可知，在基于VCG机制的价格结算中，发电商追求自身最大利润的目标与系统总发电成本最小的目标相一致，因此，出清模型式（1）～式（13）自然满足系统成本最小化。

3.3.4 收支平衡

VCG价格机制之所以能够激励发电商真实报价，原因在于这种机制令发电商自身报价的效用与其他因素施加的成本和产生的收益趋于一致，整个系统容易达到稳定和纳什均衡。在发电侧，对于任意一组给定的需求曲线，基于VCG机制的单位电价总是高于LMP。如果采用VCG价格机制向发电侧支付费用，会造成系统运营商向负荷侧收取的费用小于向发电侧支付的金额，具体数学描述为：

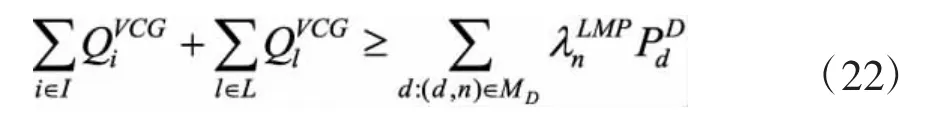
不等式左侧等于系统运营商以向参与市场的常规机组和风电机组支付的总费用，不等式右侧是向所有的负荷收取的金额。基于VCG机制的价格结算方式不满足收支平衡，其中的不平衡资金应该通过市场参与者的额外付款来补偿。然而，正如Myerson-Satterthwaite定理证明[16]，不同的补偿方式可能会导致市场效率或个体理性有所降低。

本研究提出的基于资金再分配策略（IVCG），具体分为两步执行。首先降低向发电侧的支付，即在原有的支付金额上扣减一部分金额。发电商J扣减后获得的系统支付如下：

式中：γJ为扣减费用。γJ需满足如下约束：

该不等式左边表示对发电商J的扣减费用，右边表示发电商J的净利润，表示扣减后发电商J仍自愿参与市场，申报真实发电成本。这意味着扣减费用γJ与发电商J的报价无关，不影响发电商个体理性与激励相容。

然后通过提高电价，向负荷侧收取额外费用来达到系统收支平衡，因为扣减后市场出现了新的不平衡资金△QBI：

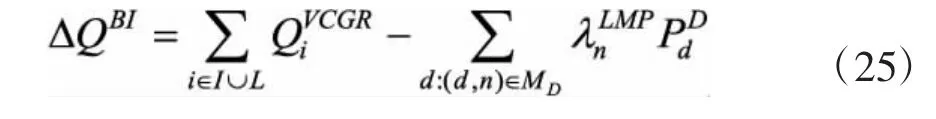
若△QBI≤0，则满足收支平衡；若△QBI＞0，需要通过提高电价向负荷侧征收额外的费用，以消除系统运营商的预算赤字。该费用可解释为，负荷侧作为发电侧真实报价的获益者，为激励发电侧真实报价而支付的信息费用。该费用产生的电价如下：

因此，将系统亏损资金分摊后的节点电价为：

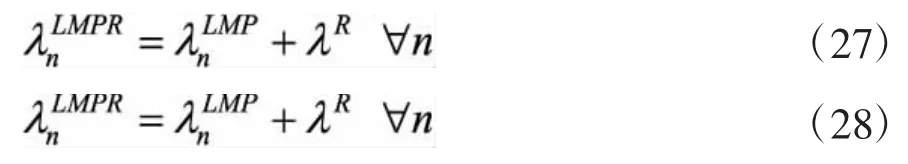
需要注意的是，本研究采用电力负荷平均分摊亏损资金的方法，实际中可以考虑按照电压等级与负荷分类和电量占比等方式进一步细分，由于篇幅的原因，在此不做展开讨论。

3.4 机制对比分析

3.4.1 算例说明

以图1所示两节点系统为例，对节点边际价格LMP和IVCG结算价格进行比较。图中发电机组G1，G2，G3，G4的真实发电成本分别为λ，3λ，3λ，2λ，节点1的负荷D1容量为2D，四台发电机的出力范围均为[0，2D]，节点1和节点2之间的线路容量为D。

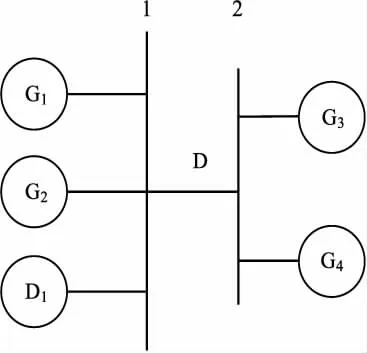
图1 两节点网络

3.4.2 实施流程

对LMP机制与IVCG机制的实施流程进行对比，可以看出IVCG价格机制只是调整了结算方式，并未改变现有电力市场基于报价的交易模式。因此，有效延续了现有的市场交易模式，具有可操作性，如图2所示。

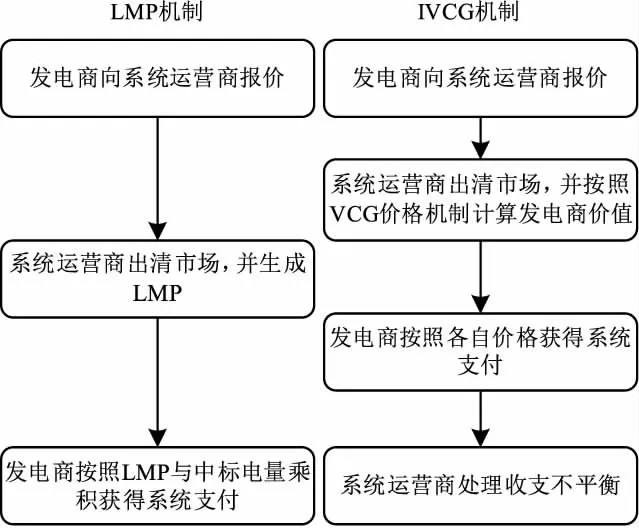
图2 LMP机制与IVCG机制的实施流程对比

3.4.3 对比分析

1）LMP机制

当各发电机组均向系统运营商申报真实发电成本时，根据模型（式（1）～式（13）），求解日前市场出清模型所得的出力计划为：

式中：X*（λ）表示4台发电机组提交真实发电成本λ=[λ，2λ，3λ，2λ]T时的最优发电出力计划向量。此时，节点1的电价为λ，4台机组的净利润均为0。然而，若发电机组G1和G4串谋，同时申报3λ-ε（ε为一极小正常数），发电机组G2和G3仍然申报真实发电成本。系统优化所得的出力计划为：

由此可见，在LMP机制下，发电机组有动机通过揣测未中标机组的价格，提供策略报价，抬高边际价格，获取更大利润。导致发电出力计划偏离最优调度运营方式，降低市场效率。因此，LMP机制难以保证系统成本最小化。

2）IVCG机制

以发电机组G1为例，当发电机组G1和G4串谋，同时申报3λ-ε时，发电机组G1和G4计划出力均为D，其余两台机组出力为0。此时除发电机组G1以外，系统其他机组的总发电成本为：

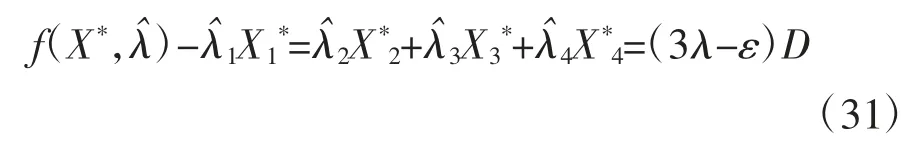
去除发电机组G1后，发电机组G2参与出力，此时，发电机组G2、G3和G4的总发电成本为：

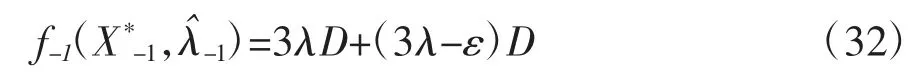
根据式（19），发电机组1的净收益为：

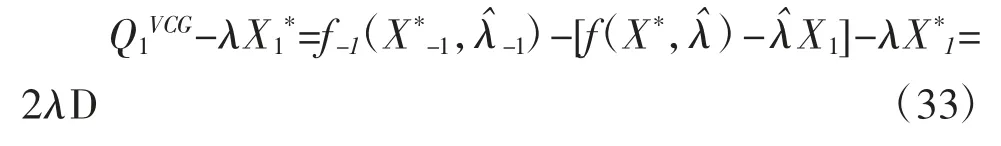
若发电机组G1选择申报真实成本λ，机组G4仍然申报3λ-ε，此时发电机组G1受系统调度出力为2D，其余不出力，除发电机组G1以外其他机组的总成本为0。当发电机组G1不参与市场时，发电机组G2和发电机组G4受调度计划出力均为D，此时系统总发电成本等于3λD+（3λ-ε）D。由此可得发电机组G1的净收益为λD+（3λ-ε）D，因为ε≤λ始终成立（否则机组G4无法中标），λD+（3λ-ε）D＞2λD关系成立。因此，对于机组G1而言，为获得更多的利润，申报真实成本为其占优策略。

4 案例仿真研究

4.1 参数设置

本研究基于IEEE-24节点系统进行案例分析。发电侧包含常规发电机组9台（即G1-G9）（表1），发电机数据被市场投标数据替代。除常规机组外，发电侧设置一处大型风电场，风电出力场景从β分布中取样[17]，形状参数（α，β）=（5，1）。初始生成500个风电机组出力场景，然后使用K-均值聚类将其缩减为3个[18]。考虑不同风电渗透率，即预测风电量除以总负载（2 200 MW）的范围为13%～53%。负载侧由7个负载组成，切负荷成本为200$/MWh。假设线路没有拥塞，不考虑输电线路电阻和无功功率。算例测试环境为HPEnvyI5-8250U笔记本电脑，编程软件为matlab R2018a，潮流计算求解器采用matpower 7.0。

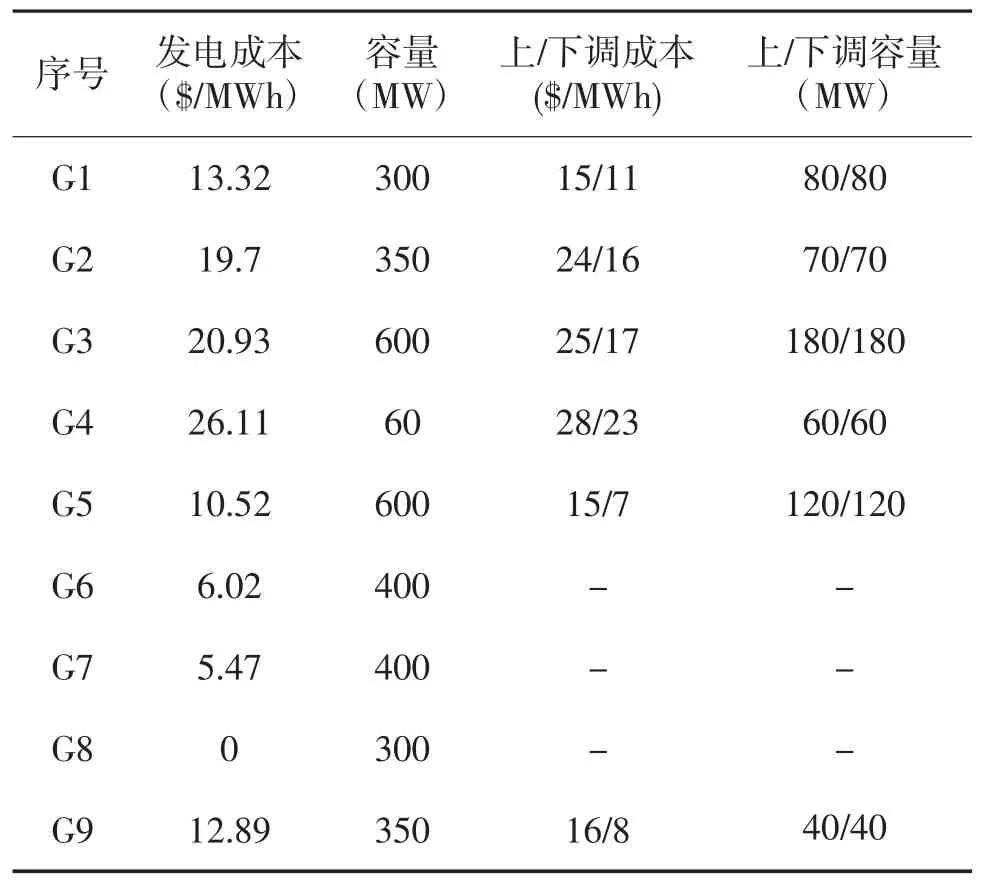
表1 IEEE-24节点系统发电机组参数

4.2 风电出力对日前出清结果的影响

根据本研究的电价机制，一台发电机组获得的支付等价于该机组参与市场时对市场中其他机组的替代效应。因此，不同于LMP机制，即使在输电网络无拥塞的情况下，电力市场也没有唯一的日前市场价格。为便于说明，本研究采用加权平均电价来进行分析，加权平均电价等于各发电商电价乘以各自出力与系统总功率之比的总和，对于常规发电商而言，加权平均电价等于λVCG，G：

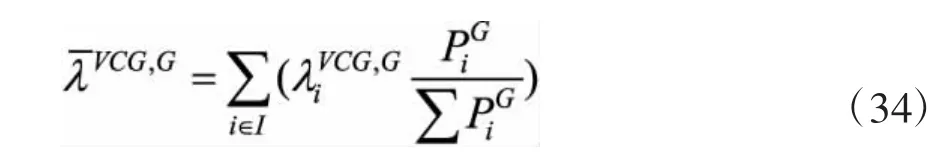
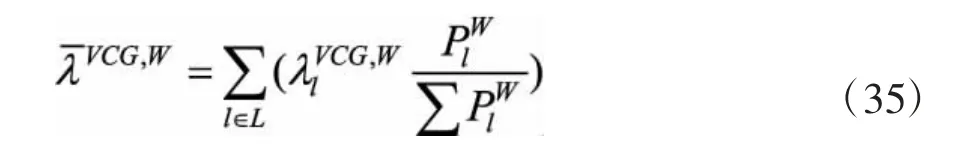
式中：风电机组l在获得的日前市场出清电价为λ1VCG，W，该机组在日前市场出清计划中的计划出力为。

图3提供了不同风电渗透率下各市场参与者的日前市场出清价格，其中负荷侧不参与竞价，采用LMP进行结算。由于负荷侧不参与竞价，负荷侧电价可视为完全竞争下的LMP，在系统不存在阻塞时，所有发电商与负荷以同样的边际价格进行出清。从图中可以看出，所有常规发电商和风电商的日前市场出清价格均大于负荷侧电价，与完全竞争情况下的边际价格相比，VCG价格产生更高的电价，这正是系统收支不平衡的潜在来源。另外，在VCG价格机制下，传统发电商的平均电价与风电渗透率并无明显的相关性，而风电商日前市场出清价格的平均值随风电渗透率的提高有所降低，这是因为VCG价格机制是根据市场成员间的替代效应定义其价值，并按照该价值结算。表2所示的分析结果验证了负荷侧电价由边际发电商决定，随着风电渗透率提高，负荷侧电价呈下降趋势，最终导致系统运营商的预算赤字增加。

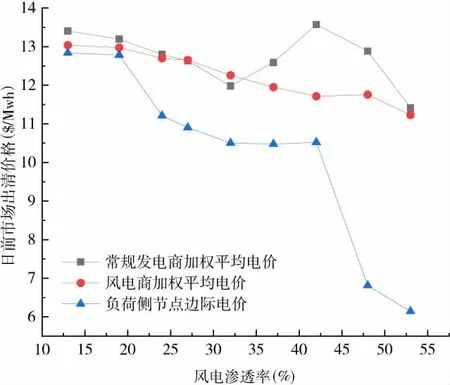
图3 不同风电渗透率下的日前市场出清价格

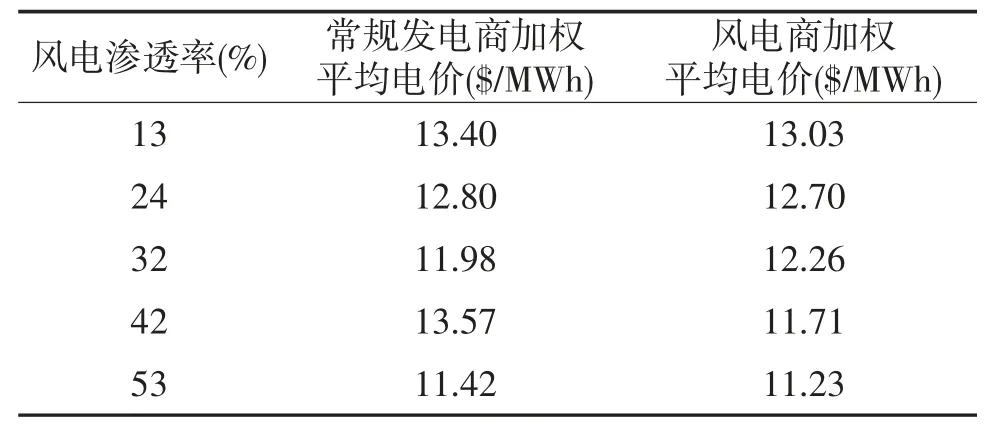
表2 风电渗透率对不同发电商加权平均电价的影响对比

图4是不同风电渗透率下各常规机组的净利润。所有参与市场的常规发电商，利润均非负，说明VCG价格机制可以实现发电商成本回收，满足个体理性。并且随着风电渗透率的提高，常规机组获得利润的总体水平有所下降。

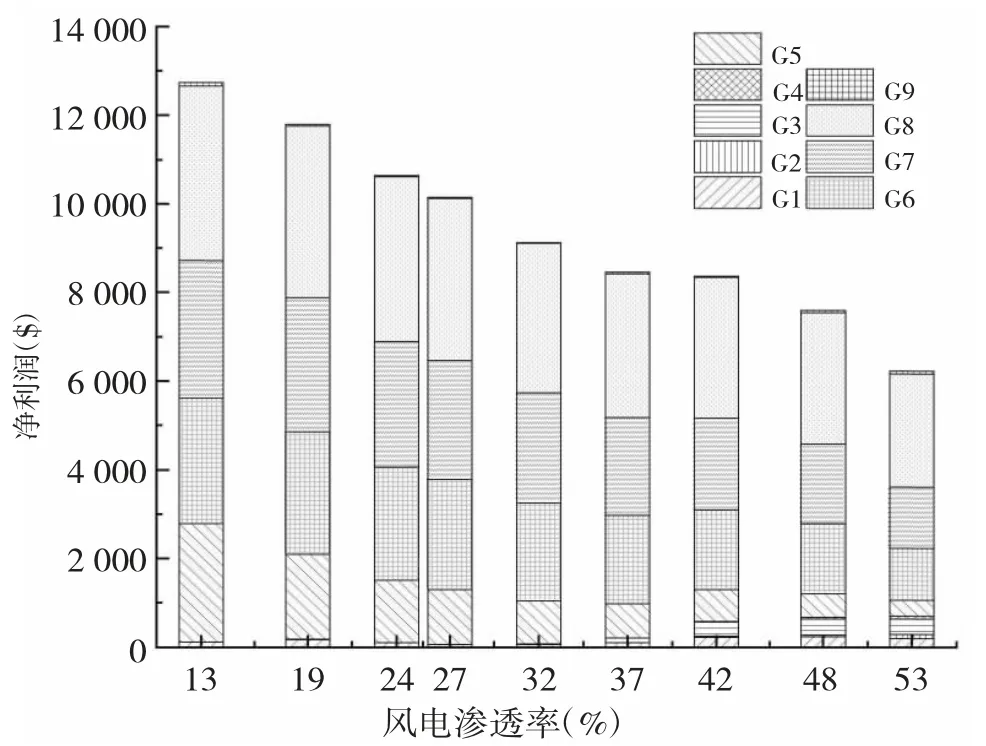
图4 不同风电渗透率下各常规机组净利润

4.3 收支平衡分析

不同风电渗透率下系统收支费用如图5所示，当风电渗透率为13%，系统边际电价为12.83 $/MWh，总负荷水平为2 200 MW，因此，从负荷侧收取的费用总和为28 226 $，而需要支付给发电机组的总金额为29 370$，比负荷侧收费高出4.05%。而随着风电渗透率的不断提高，系统运营商的预算赤字将不断增大。表3为不同风电渗透率下，系统运营商的收支比。

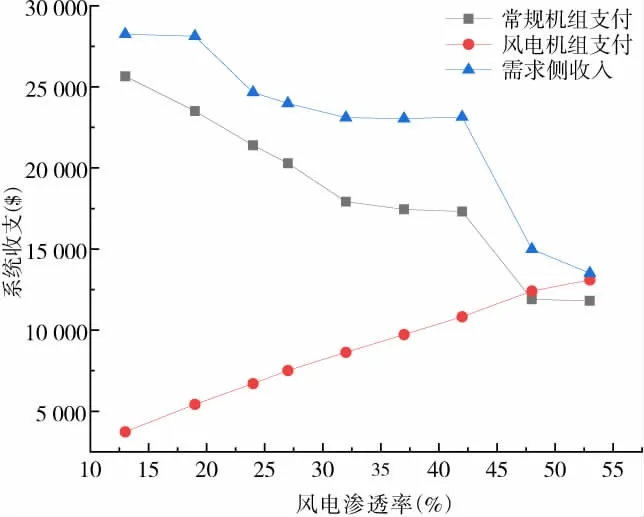
图5 不同风电渗透率下系统收支费用

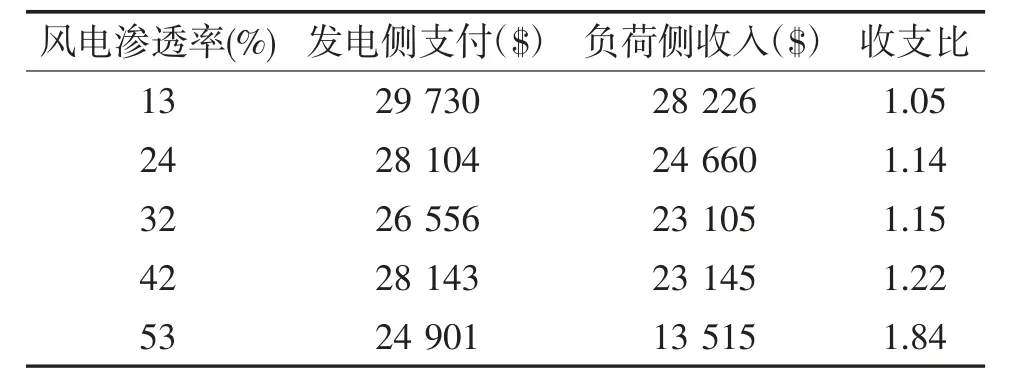
表3 风电渗透率与系统运营商的收支比关系

本研究提出的IVCG采取一种可行收支平衡策略，每个发电商的收益减去一个常数，该常数可选择上限为各发电机组净利润的最小值。当风电渗透率等于13%时，发电机组G2，G3，G4不参与日前市场出清计划。发电机组G9净利润为81 $，在所有参与出清的发电机组中最低。本算例选择该净利润的百分之八十作为扣减费用，即向每一台发电机组的支付费用扣减64 $。扣减后系统向发电侧支付的总费用为28 986 $。然而，系统运营商从发电侧收取的费用总和为28 226 $，仍无法满足收支平衡。根据负荷侧分摊策略，将剩余系统亏损资金向负荷侧进行分摊，分摊后负荷侧的节点电价为13.84$/MWh+0.35$/MWh=14.19 $/MWh。此时，系统满足收支平衡。

5 结语

本研究提出的IVCG电价机制具有两阶段市场出清特征，该电价机制满足激励相容、个体理性以及系统总成本最小化性质，并且在IEEE 24节点算例中进行验证分析，结果表明：（1）在本研究IVCG电价机制下，所有发电商参与市场的占优策略是申报其真实发电成本；（2）参与日前市场的所有发电机组净利润均大于等于0，说明该机制满足个体理性；（3）日前市场出清电价与风电渗透率具有相关性。随着我国“碳达峰、碳中和”发展目标的提出，电力市场建设需要考虑的因素更加复杂。本研究通过开展电价机制研究，从电力市场角度为提升新能源消纳水平提供了理论依据。