基于离散粒子群算法的复杂曲面微小零件切削参数优化研究
吴昊,江洁
红河学院工学院
1 引言
随着信息化和工业化的迅速发展,制造业有效带动了国民经济发展,数控加工技术成为制造业的是重要分支,数控加工以机床为基础,根据工件图纸要求,发挥计算机、自动化及柔性制造等技术优势,并通过合理选择切削参数获得最佳切削效果,实现机械加工全过程的连续性。切削参数直接关系到加工零件的质量,现如今机械制造材料趋于轻量化,加工零件更加高端和精细,但微小零件曲面结构复杂,机床和刀具获取的数控切削加工参数有限,还需操作人员依靠经验获得,导致缺乏有效的切削数据库支撑,加工后的微小零件难以满足实际设计需求。因此,对复杂曲面微小零件切削参数优化进行研究,对优选加工工艺的切削参数、减少微小零件切削时间、提升材料去除速率以及缩短辅助工时具有重要意义[1]。
现阶段,微小零件切削参数相关研究已取得较大进展,包括数字化处理微小零件的加工要求和加工条件,将切削参数优化问题转换为条件极值问题,综合考虑不同的约束条件(微小零件的材料信息和加工特征等),沿走刀路径对切削加工动力学进行建模,预测切削过程的物理量(振动、切削力、扭矩及功率等),描述物理量与机床刀具几何参数、切削条件之间的经验公式,形成优化的数控加工切削参数数据库[2]。
常规切削参数优化方法存在零件加工表面粗糙度较高且零件加工工序总工时较长的问题,零件表面质量和加工效率得不到充分保障,为解决这一问题,结合以上理论,提出基于离散粒子群算法的复杂曲面微小零件切削参数优化方法。
2 基于离散粒子群算法的复杂曲面微小零件设计切削参数优化方法
2.1 计算切削参数优化目标函数
选择复杂曲面微小零件待优化的切削参数,确定切削参数优化的目标方向。在微小零件切削加工过程中筛选可操控变量,从中挑选持续变化的变量,最后选择切削速度和进给量作为待优化切削参数。建立提高生产效率的目标函数,计算微小零件切削时间T2为
(1)
式中,A为刀具头数;a为刀具转数;c为切削速度;B为刀具模数;C为切出长度;b为切入长度;e为走刀数量[3]。
每道工序平均换刀时间T3为
(2)
式中,F为刀具磨损的换刀时间;g为刀具耐用度系数;c为刀具直径;G为刀具齿数;H为刀具纵向的每齿进给量;d为切削宽度;h为切削深度。
批量生产微小零件,确定完成微小零件加工过程的工序用时,其计算公式为
T1=T2+T3+T4+T5+T6
(3)
式中,T1为一个零件加工过程总时间;T4为零件装夹时间;T5为空行程时间;T6为辅助时间。
建立降低生产成本的目标函数,计算一道工序的工艺加工成本D1为
(4)
式中,D2为微小零件毛坯成本;D3为单位时间人力成本;D4为单位时间机床损坏成本;D5为刀具成本[4]。
引入相关参数f,将式(3)和式(4)表示的两个优化目标转换为单个目标进行优化,变换后的切削参数优化目标函数表达式为
(5)
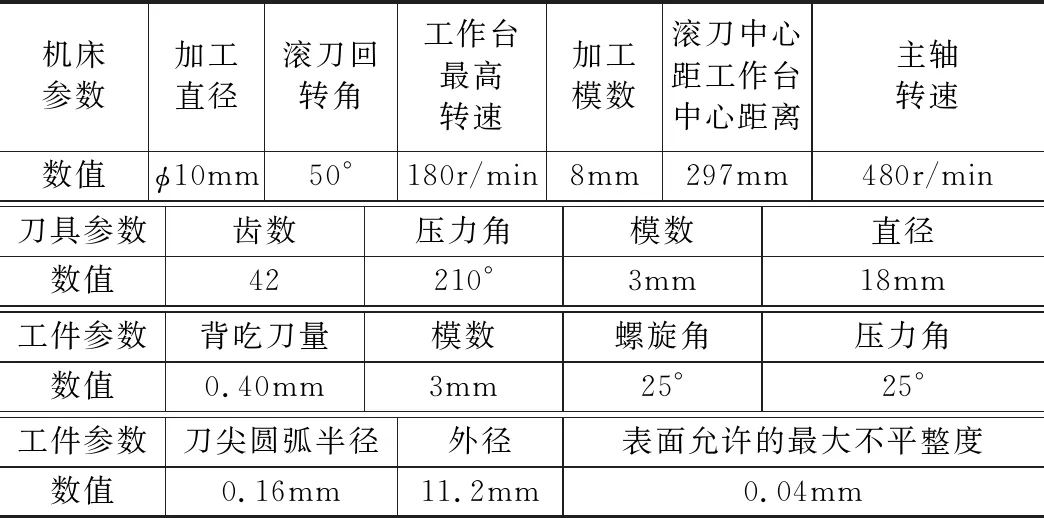
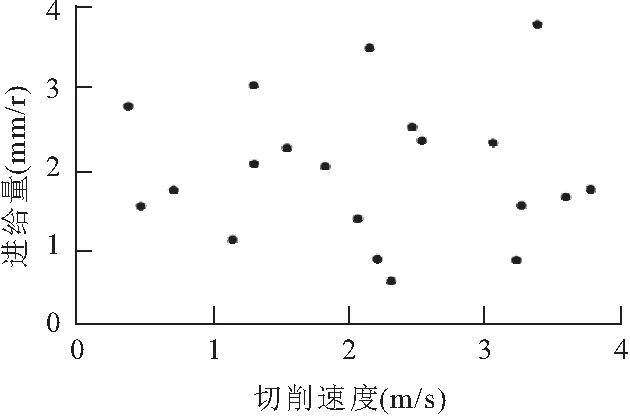
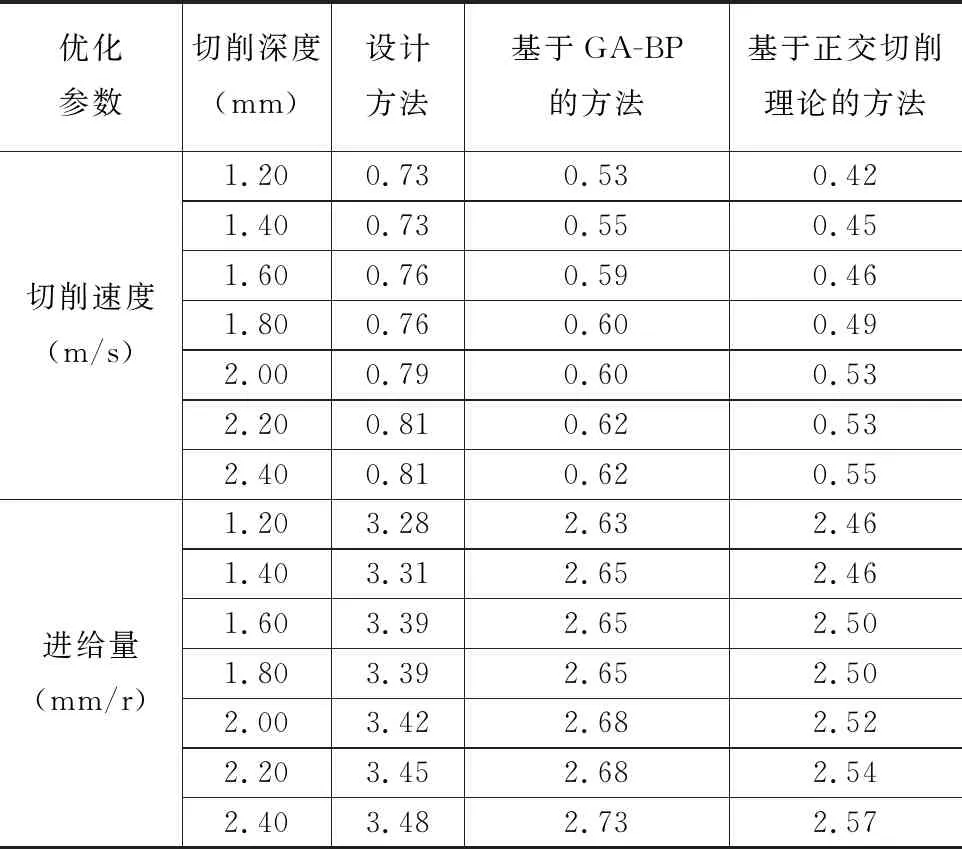
式中,当f=1时,提高生产效率为变换目标函数的优化方向;f=0时,降低生产成本为变换目标函数的优化方向;0 选择与微小零件切削参数优化结果密切相关的影响因素,令切削参数满足各影响因素符合实际的约束条件。约束切削过程中的主轴功率,令其不超过机床主轴额定功率,约束条件为 Ic-JPmax≤0 (6) 式中,I为刀具在主运动方向上的力;c为切削能耗;J为机床运行速率;Pmax为主轴功率最大值。 对切削零件的作用力进行约束,令施加的切削力在机床主轴允许范围内,以降低机床磨损程度,此过程需满足 I-MLmax≤0 (7) 式中,Lmax为主轴最大切削力;M为进给速度。 微小零件切削时间延长情况下,判定刀具会磨钝,且将影响零件表面质量和切削效率,甚至完全不能工作。根据刀具寿命的最大值和最小值,建立刀具寿命对切削参数选择额的约束条件,确保切削参数不超过机床有效范围,其约束条件为 (8) 式中,dmin,dmax为切削宽度极值;hmin,hmax为切削深度极值;Mmin,Mmax为进给速度极值;Nmin,Nmax为刀具转速极值[5];N为刀具转速。 约束零件切削过程中的进给量,令其满足机床进给约束,有 (9) 式中,n为微小零件工件直径;P为刀具每齿进给量。 约束零件加工表面粗糙度,有 (10) 式中,qmax为粗糙度最大值;O为刀尖圆弧半径。 设主轴最大扭矩为pmax,约束切削扭矩,有 (11) 由式(6)和式(11)组成切削参数优化约束条件。 利用目标函数和约束条件对参数优化问题进行建模,通过粒子群算法求解模型。设第i个约束条件为Ri,i=1,2,…,6,模型表达式为 (12) 将约束条件融入参数优化目标函数,在目标函数上附加一个惩罚项,得到非线性方程表达式为 (13) 式中,ri表示约束条件是否满足,当Ri(c,P)<0时,ri=0,当Ri(c,P)>0时,ri=1;Q为罚因子。 采用离散粒子群算法搜索非线性方程的全局最优解并定义粒子属性,利用粒子位置表示切削速度和进给量的一个潜在解,将式(13)作为评价函数,利用评价值比较各粒子位置的好坏,利用粒子速度确定粒子飞行情况,移动区域内的粒子并改变粒子位置。由多个粒子组成一个种群,对种群进行多次迭代,不断改变各个粒子的位置、速度和评价值,找到整个群落中评价值最高的粒子。通过罚因子Q惩罚违反约束的粒子,设置每个约束条件的可行域宽度。当粒子位置与可行域距离过远时,增加粒子评价函数的罚因子,使粒子受到较大惩罚,促使粒子飞行至可行域移动;当粒子靠近可行域边界时,适当减小罚因子的取值,减小粒子受到的惩罚力度,使满足约束条件的粒子均能够存活。初始化可行域内的粒子评价值极值,比较各个粒子评价值,得到种群全局极值,更新粒子属性,其计算公式为 (14) 式中,St,St+1分别为t时刻、t+1时刻的粒子速度;u为权重初始值;U1,U2为加速度参数;Wt,Yt分别为粒子个体、种群全局的评价值极值;Xt,Xt+1分别为t时刻、t+1时刻的粒子位置;s1,s2为[0,1]区间内的随机常数。 计算更新后粒子的评价值,令每个粒子产生相邻粒子,计算相邻粒子评价值,比较粒子与相邻粒子的评价值大小,留下加高评价的粒子状态,继续更新粒子和种群的评价值极值。重复以上流程,将目标函数作为迭代终止标准,当粒子位置满足终止标准后,停止离散粒子群的循环,输出切削速度c和进给量P的最优解。至此完成复杂曲面微小零件最优切削参数的求解,实现基于离散粒子群算法的复杂曲面微小零件切削参数优化方法设计。 将此设计方法与基于GA-BP的切削参数优化方法、基于正交切削理论的切削参数优化方法进行对比试验,比较三种优化方法作用下的零件加工表面粗糙度和零件加工总时间。 待加工的复杂曲面微小零件为滚齿加工,工件材料为Q235普通碳素钢,毛坯为40.0mm×38.0mm×21.0mm(长×宽×高),齿数为42。选择YKS3120A立式加工中心,主轴电机最大功率为34kW,最大主轴转速为16000r/min。刀具为镶齿盘铣刀,刀具材料为YG6硬质合金,刀片数为2,悬长为80mm,转位2次,刀具耐用系数为0.83,主偏角为70°,刀粒数为70。由生产数据和生产工艺方案可知,毛坯成本为28元,单位时间劳动成本为0.3元/min,刀具成本为220元,单位时间机床磨损成本为2.3元/min。机床、刀具和工件的技术参数具体如表1所示。 表1 滚齿加工技术参数 滚齿加工试验在VMC高速加工中心上进行,零件加工环境如图1所示。 图1 毛坯加工过程 采用外圆纵车加工,且加工过程不用切削液,选择表1所示的技术参数作为基础工艺参数,齿轮毛坯经一次滚齿加工完成,加工余量为0.8mm。 根据VMC高速加工中心的实际情况,分析生产效率和生产成本所占比例的权重,确定优化相关系数f=0.3,构建参数优化数学模型。编写并运行离散粒子群算法程序,设置最大迭代次数为250,U1,U2为1.82673,u为1.3。随着迭代次数的增加,u递减至0.3,罚因子为10,滚齿加工的粒子群优化过程如图2所示。 (a)第0代粒子分布 由图可见,第0次迭代时,粒子分布在约束条件的可行域范围内,切削速度位于[0,4],进给量位于[0,4],粒子分布散乱,没有汇聚倾向;第50次迭代时,切削速度位于[0,2],进给量位于[0,4];第100次迭代时,切削速度位于[0,1],进给量位于[2.5,4];第150次迭代时,粒子汇聚于一点,该点即为切削速度和进给量的最优解。 改变齿轮毛坯的切削深度,用三种方法分别计算不同切削深度下的切削参数最优解,优化结果如表2所示。 表2 齿轮毛坯切削参数优化结果 3.3.1 表面粗糙度测试 分别应用三种方法优化的切削参数对齿轮毛坯进行加工,测试齿轮加工表面粗糙度。由于齿轮粗糙度与齿轮使用寿命关联紧密,粗糙度越低,齿轮间隙越小,运转时受到的冲击负荷越低,齿轮磨损程度就越低。使用表面粗糙度轮廓仪,手持2μm金刚石触针,沿着滚齿表面缓慢滑行,记录并显示被测表面轮廓曲线,得到粗糙度测量结果,各类切削深度分别测量20个滚齿。三种方法实验对比结果见图3。 要求该批次的滚齿表面粗糙度小于0.7μm,由图3可知,三种方法优化后的加工零件粗糙度普遍满足设计要求,其中,本文设计方法的滚齿表面粗糙度均值为2.1μm,基于GA-BP的切削参数优化方法粗糙度均值为5.0μm,基于正交切削理论的切削参数优化方法粗糙度均值为6.4μm,平均粗糙度分别减小了2.9μm,4.3μm,且零件表面更加平滑,加工精度更高。 图3 滚齿加工表面粗糙度实验对比结果 3.3.2 总工时测试 针对每类切削深度,采用三种方法分别连续加工20个齿轮毛坯,得到滚齿成品,记录每个齿轮加工总工时。零件加工总时间实验对比结果见图4。 图4 零件加工总工时实验对比结果 由图可知,优化设计方法后,齿轮的平均加工总工时为34s,另外两种方法平均加工总工时分别为65s,79s,优化设计方法齿轮的加工总工时分别缩短了31s,45s。 综上所述,优化设计方法的齿轮加工表面粗糙度较另外两种方法有所减小,缩短了齿轮加工总工时,提高了滚齿的表面质量和生产效率,更好地促进了齿轮切削加工作业。 充分发挥离散粒子群算法的优势,设计了一种复杂曲面微小零件切削参数优化方法,获得最优切削速度和最优进给量,提高了加工精度和加工效率。但此设计方法仍存在一些不足,在今后的研究中,为准确预测零件切削过程中的物理现象,需考虑工件具体结构,细化和扩展微小零件的加工特征,对加工特征进行建模,计算出更符合实际情况的优化切削参数。2.2 计算切削参数优化约束条件

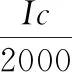
2.3 求解最优切削参数
3 优化案例分析
3.1 加工参数
3.2 设计方法优化过程

3.3 实验结果分析


4 结语

