基于钻孔数据的盾构隧道纵向结构参数化计算

李霖皓, 陈 珂, 胡云华, 龙 凡

(1. 华中科技大学土木与水利工程学院, 湖北 武汉 430074; 2. 华中科技大学人工智能研究院，湖北 武汉 430074; 3. 武汉市政工程设计研究院有限责任公司, 湖北 武汉 430023)

0 引言

随着城市地下空间建设的需求不断提升，长距离、大直径的盾构隧道建造技术逐步成为地下工程的一个重要发展方向[1]。然而，长距离隧道通常穿越软硬不均的地层，有时还会存在超载及大坡度区间，其纵向不均匀沉降与变形差异问题日渐凸显[2]。盾构隧道结构计算的主要目的是根据外部荷载条件与结构尺寸参数，验算其结构变形是否处于设计规范容许范围内。其中，影响结构性能的参数有管片宽度、衬砌厚度、接头数量等，荷载条件包括土压力、水压力、地面超载、结构自重等。

为了在隧道设计中充分考虑覆土埋深对纵向结构的受力与变形影响，结构计算模型需要从二维向三维过渡，以输出更精细的设计结果。另外，考虑到隧道的纵向结构呈狭长带状分布[3]，其与地质体具有强关联性，因此永久荷载除结构自重外还包含来自周围的土压力与水压力。然而，土/水压力值的计算依赖于对地质勘察中地质钻孔信息的选取，具体取值受限于设计人员的经验，通常采取就近原则或假定最不利条件进行考虑。因此，隧道纵向结构计算需要对钻孔数据进行高效挖掘，确保设计可靠。

近年来，参数化设计在隧道结构设计中受到国内外研究人员的广泛关注。Caetano等[4]介绍了国内外对参数化设计的定义，肯定其在建筑工程项目中有助于确定设计约束。Ninic等[5]将参数化隧道模型和数值模型整合在一起，对盾构施工过程进行仿真分析。Luo等[6]根据盾构衬砌的几何特征结合参数化设计方法，形成了盾构隧道自动建模和管片排版工具。Sharafat等[7]将一系列算法引入到隧道信息模型中，以适应不同的隧道设计。Peng等[8]利用参数化数字模型将盾构施工过程中的隧道结构信息反馈给各个参与方。Song等[9]将参数化设计与信息管理技术相结合，实现对隧道工程各阶段、各专业设计的高效管理。Zhou等[10]利用参数化设计方法开发了基于IFC的管片拼装系统，支持盾构施工信息传递。相比于传统计算机辅助设计，参数化设计可以提升复杂构件建模、修改和出图的效率，现阶段设计人员主要利用其进行管片建模、排版[11]与线路设计[12]，却忽略了结构构件计算与设计结果的可靠性分析，因此参数化设计仍有大量提升空间。

盾构隧道的参数化设计在结构验算方面仍需开展进一步研究应用，特别是针对纵向结构，需要解决的关键问题在于： 如何将地质数据与结构模型进行关联，继而通过参数化手段驱动结构计算。因此，本研究: 1)基于地勘钻孔数据建立地层数据库，并按需输出对应隧道区间的约束条件与荷载参数； 2)基于参数化建模方法确定隧道纵向结构计算模型； 3)将地层数据库与纵向结构模型建立引用关系，实现隧道纵向结构的参数化计算； 4)以武汉市两湖隧道(东湖段)项目为设计实例，对所提出的方法进行应用验证。

1 地层数据库的建立

1.1 集成钻孔数据

地质勘察通常是按照钻探、采样等确定性的方法来认识地质环境，并将钻孔样本和勘测数据作为依据。为了解决钻孔密度受限与地质变异性等问题，国内外许多学者采用克里金法、贝叶斯推理框架、模糊推理系统、K最近邻算法(KNN)等方法来解决地质不确定性预测、地质物理反演、地质灾害敏感性评价以及钻探预测模型建立等问题[13-16]。其中，KNN能基于已知钻探结果对未知或不确定钻探结果进行预测；克里金法能通过协方差函数进行高程预测(插值)。因此，本研究基于已有的地质钻孔数据，利用KNN进行地质解析; 利用普通克里金(ordinary Kriging)算法进行水位高程预测。钻孔数据的编译、存储、传递通过Python中Pandas工具包的DataFrame(数据框，下同)函数进行，即以目标空间内地质钻孔中土层分布数据与水位高程数据为学习样本，推断未钻探地区的地层边界与高程，并对推断结果建立数据框格式的地层数据库。地质解析过程主要包括以下步骤：

1)细分地勘钻孔数据，整理形成数据框D。原始钻孔数据的采集格式如表1所示。

表1 地勘钻孔数据的格式

对于Dzk，同一个地勘数据钻孔有不同的土层分布，从上到下依次填写每一钻孔下各土层的上界面和下界面的高程以及土层代码。对以上表格内的数据进行一定间隔的细分，生成分布更规律、更密集并带有土层代码的点，最终形成新的地勘钻孔数据n行5列数据框，即

2)提取数据框D中的三维坐标点(D[:,1]，D[:,2]，D[:,3])导入到参数化建模软件(如Rhino & Grasshopper)中进行钻孔点云建模P，即

3)读取划分单元的地勘钻孔土层代码D[:,4]，分析出总共出现的土层种数，并对每种土层进行标签设定。土层种数分析和土层类型的标定算法如下：

算法1根据输入每个钻孔下的土层分布分析总共出现的土层种数并进行标定

输入:每个钻孔的土层分布，D[:,4]

输出:土层类型list，SoilList

1. 给SoilList对象赋予空列表

2.foriinrange(D[:,4]的长度):

3.ifSoilList中D[:,4][i]对象出现的次数为0：

4. 给SoilList添加D[:,4][i]对象

5.returnSoilList

4)依次对目标空间中每个单元网格节点V和钻孔点云模型P进行最小距离计算，利用KNN推断出每个网格节点的最大似然土层种类，并赋予相应的标签，生成带有土层信息标签的V′，即

式中V为n行3列数据框，包含n个单元网格节点中的坐标信息。

用于分析每个网格节点所属最大似然土层种类的算法如下：

算法2基于KNN的土层分类

输入：点云模型,P； 对应点云模型的土层信息列表,D[:,4]；网格节点列表，V； KNN参数，k(必须为奇数)

输出:带有土层信息的网格节点数据框V′

1.foriinrange(V的列表长度):

2.forfinrange(P的列表长度)：

3. 求解V[i]与P[f]的距离

4. 挑选在P中与V[i]距离最小的k个点

5. 确定这k个点在D[:,4]对应的土层信息，并返回重复频率最高的土层名称

6. 将该土层名称添加入V′[i]

7.returnV′

1.2 水位面高程分析

水位高程预测过程主要包括以下步骤：

1)从地勘钻孔数据中单独提取水位线高度的空间坐标，整理形成数据框W，即

式中h为水位线高程值。

2)调用Python中Pykrige工具包，导入数据框W进行普通克里金模型训练。训练得到的模型将利用Pickle工具包进行储存。

3)确定目标空间内某点位的平面坐标(x，y)后，将其输入已训练的普通克里金模型中并输出预测的水位高程h，记为水位点(x，y，h)。

1.3 任意剖面下土层参数与水位标高输出

基于钻孔数据，对目标空间建立数据框形式的地层数据库，然后按照设计要求确定具体需要解析的盾构断面位置，依照该位置的平面坐标和训练得到的普通克里金模型可以推测出该断面的水位标高； 同时，依照该位置的空间参数(距离、位置)对目标空间进行精确剖切，计算出剖切面中每种土层下z坐标(V′[:,2])的高程范围，最终输出该断面下每种土层的平均厚度与排列顺序。确定该断面土层厚度的算法如下：

算法3计算某地层断面中分布的各土层厚度

输入:某地层断面中带有土层信息的网格节点数据框，V′

输出:该断面沿z坐标从高到低方向上每种土层的厚度，SoilDepthList

1.计算V′中z轴坐标最高的10个点的z坐标平均值，并以该值为地表高度，A

2. 计算V′中每组土层中z轴坐标值最低的10个点的z坐标平均值，并按升序排列入表格，List

3.SoilDepthList= [ ]

4.foriinrange(List的长度):

5. SoilDepthList.append(List [i]-A)

6.A=List[i]

7.returnSoilDepthList

为了进一步让设计人员对解析和预测结果有更直观的理解，本方法可以根据地质标签赋予相应的颜色参数RGB值，然后在参数化建模软件中进行网格节点着色处理，同时对水位点进行嵌面拟合生成水位面，最终实现地层数字化和可视化。

1.4 水土压力计算

水压力和土压力作为地层因素影响隧道结构，是隧道结构设计中必须考虑的准永久荷载。一般来说，计算水土压力有水土分算与水土合算2种方法。前者适用于砂质土地层，将水压力分离出来，根据地下水位高程将土压力按照干重度和饱和重度分开计算；后者适用于黏性土地层，将水压力作为一种新的土压力进行考虑。同时，作用在隧道结构体的水土压力分为垂直方向和水平方向。水平土压力的大小由垂直土压力乘以土的侧压力系数K0确定；而水压力的水平和垂直方向可视为近似相等。

根据规范GB/T 51438—2021[17]，对于埋深小于2倍外径的浅埋隧道和软土盾构隧道可采用全覆土压力计算。

H=∑Hi+∑Hj

；

(1)

pe=∑γiHi+ ∑γjHj

。

(2)

式(1)—(2)中：H为该点的总覆土埋深，m；Hi为第i层土的厚度，m；Hj为第j层土的厚度，m；pe为垂直土压力，kPa；γi为第i层土的天然重度，kN/m3；γj为第j层土的天然重度，kN/m3。

对于目标空间内任意一点的水压力可以采用静水压力计算，则有：

pw=γwHw

。

(3)

式中：γw为水的重度，kN/m3；Hw为隧道结构以上地下水位高程，m；pw为水压力，kPa。

2 隧道纵向结构力学模型

2.1 等效刚度梁

隧道纵向结构内力计算一般采用2种模型，即纵向梁-弹簧模型和纵向等效刚度梁模型。后者与前者相比，具有模型简单、参数较少等优点[18-19]。纵向等效刚度梁模型主要是将环间接头因素转化为刚度折减，并用折减后的等效刚度均匀梁进行替代；结构的约束条件需引入地层弹簧来模拟结构与地层间的相互作用；外部荷载主要考虑垂直方向上的水土压力，其模型简图如图1所示。

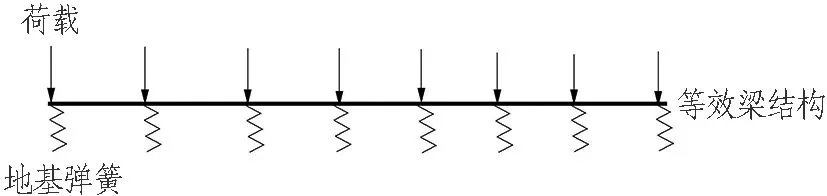
图1 等效刚度梁模型简图

通过该方法既能考虑接头对隧道结构性能的影响，也可以将不连续的隧道结构连续化。其中，地层弹簧的弹性刚度用岩土体的垂直基床系数来替代，折减后的等效抗压刚度为

(4)

折减后的等效抗拉刚度为

(5)

折减后的等效抗弯刚度为

(6)

(7)

式(4)—(7)中：Es为管片环的弹性模量，GPa；As为管片环的断面面积，m2；Kj为环间接头轴向弹簧系数的总和，kN/m；ls为管片宽度，m；φ为中位轴位置的角度，rad；Is为管片环的断面惯性矩，mm4。

2.2 基于Karamba 3D平台的参数化有限元结构建模

为了实现高效的参数化有限元结构分析，本方法利用Karamba 3D 2.2.0进行隧道纵向结构计算。Karamba 3D可以用编程的方式实现结构计算与结果可视化[20]，其计算流程如图2所示。其中，结构模型导入可以直接调用Rhino & Gasshopper所生成的geometry对象，节点数据导入可以利用Python语言进行编译和传输。组建模型完成后输出的计算结果是以单元节点顺序排列的树形数据框结构。

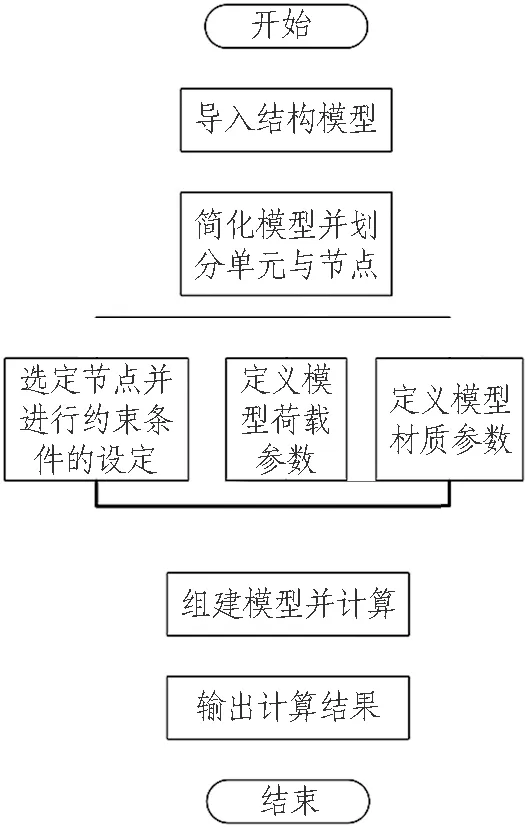
图2 Karamba参数化结构计算操作步骤

对于组建隧道纵向结构的计算模型，其参数输入过程主要包括以下步骤：

1)根据Luo等[6]提出的隧道管片参数化建模方法利用Rhino & Grasshopper输出隧道三维中心线模型。该模型是由等长度的线段依次首尾相连而成，每条线段可视为每环管片的中心轴。在结构计算中，每条线段将视作一个梁结构单元，线段的首端点与末端点作为梁结构模型的节点。

2)对每个节点施加荷载。由于隧道纵向结构计算主要针对沉降变形问题，所以荷载仅考虑垂直土压力与垂直水压力。每个节点由于所处空间位置不同，水土压力大小也会有区别。所以每个节点的荷载需要参考算法3输出的断面土层参数并根据式(1)—(3)求得。

3)对每个节点施加土弹簧。土弹簧的上端与梁单元节点刚性接触，下端完全固定。每个土弹簧所属的地质标签通过算法2求得。每个弹簧的弹性刚度可以根据地勘报告中对应的岩土体设计参数建议值(垂直基床系数Kv)选取。

2.3 将结构模型与地层数据库建立引用关系

将每个节点所施加的约束条件与地层数据库建立引用关系，即基于算法2和算法3通过执行循环依次计算出每个梁单元节点的总荷载与地基弹簧刚度，再依次输入进Karamba 3D结构模型中，从而使约束条件可以根据地层数据的改变而变化。具体算法如下：

算法4计算目标空间下结构各节点的荷载与地基弹簧刚度参数

输入:目标空间下结构节点的坐标数据框，N

输出:该结构每个节点的土弹簧弹性刚度、垂直土压力、垂直水压力的分布数据框，C

1. 创建N行4列空的数据框，C

2.foriinrange(len(N[:,0])):

3. 将节点(N[i,0]，N[i,1]，N[i,2])代入算法2求得所属土层名称

4. 根据地勘报告并输出该土层的地基弹簧刚度，K

5. 匹配节点(N[i,0]，N[i,1]，N[i,2])所在盾构轴线的里程并对该里程的盾构断面进行剖切，生成V

6. 将V代入算法2求得V′

7. 用V′代入算法算法3求得该节点垂直方向的各土层厚度SoilDepthList与地下水位高程Hw

8. 提取SoilDepthList中的参数代入式(1)—(3)求得pe、pw

9.将K、pe、pw赋予数据框C[i,0],C[i,1],C[i,2]

10.returnC

3 案例验证

为了验证本方法的有效性，引入武汉市两湖隧道东湖段某100 m区间隧道为验算对象，并与现有方法(基于SAP84软件)的计算结果进行对比。

两湖隧道东湖段位于武昌中心城区南北向中轴线位置，是当前世界上规模最大的城市湖底、双层超大直径盾构隧道。其中，位于东湖路接线的QXK6+300～+400区间(100 m)穿越软硬不均的强/中风化岩层，且由于风光堤的存在导致地面荷载变化较大。依据该项目第三方审查单位的建议与规范要求，有必要对该区间隧道进行纵向变形和强度分析。

借助Python中的for循环与Grasshopper Cycle执行算法2和算法3，每隔1 m自动输出水土压力参数，同时对该隧道区间下每隔10 m的地质纵向剖面进行可视化处理，结果如图3所示。隧道中轴线穿越了强/中风化岩层、粉质黏土，与地勘分析结果一致。

图3 QXK6+300～+400区间数字化地层剖面图

图4展示了2种方法构建的结构计算模型，单元划分精度为1 m(环宽2 m)，土弹簧每隔1 m布置1个。相比SAP84软件使用的计算方法，本方法所提出的参数化结构计算模型不仅能保持隧道轴线的三维线性特征，而且荷载与约束条件也能根据编程命令自动设定。其中，结构单元参数统一设置为： 管片直径14.5 m、厚度600 mm、弹性模量34.5 GPa、剪切模量14.4 GPa、比重24.5 kN/m3。环间接头采用36个8.8级斜螺栓(M36)。根据式(4)—(7)计算出等效抗拉刚度折减系数和等效抗弯刚度折减系数分别为0.021和0.056。

(a) 本文方法

图5比较了2种结构计算模型的荷载与约束条件，图6展示了2种方法计算出的结构纵向位移结果。由于本方法通过算法4自动计算并导出的约束与荷载参数与SAP84软件基于人工经验和最不利条件确定的参数存在区别，导致二者计算结果存在一定偏差，但本方法计算结果更接近实际。根据规范GB 50446—2017中对管片结构沉降累计值的要求，2种结果都在10 mm范围内。根据本方法的计算结果，利用Rhino & Grasshopper中的curve curvature分析工具计算其纵向变形曲率半径最小为16 487.02 m， 大于结构安全控制指标15 000 m。

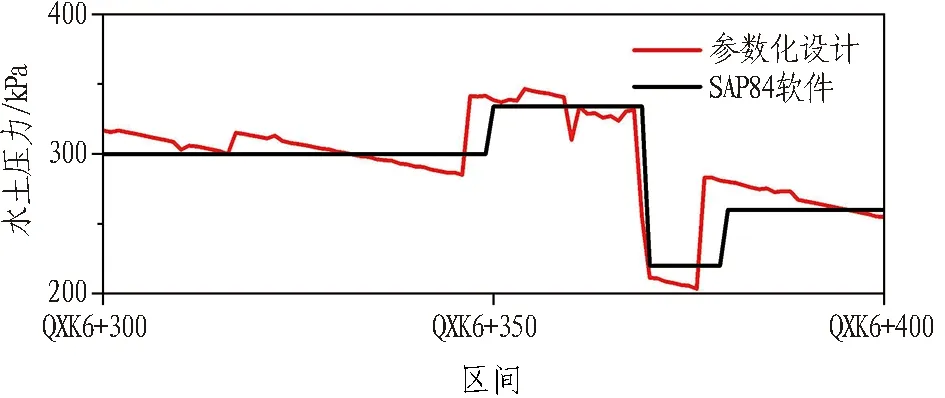
(a) 盾构区间内水土压力分布

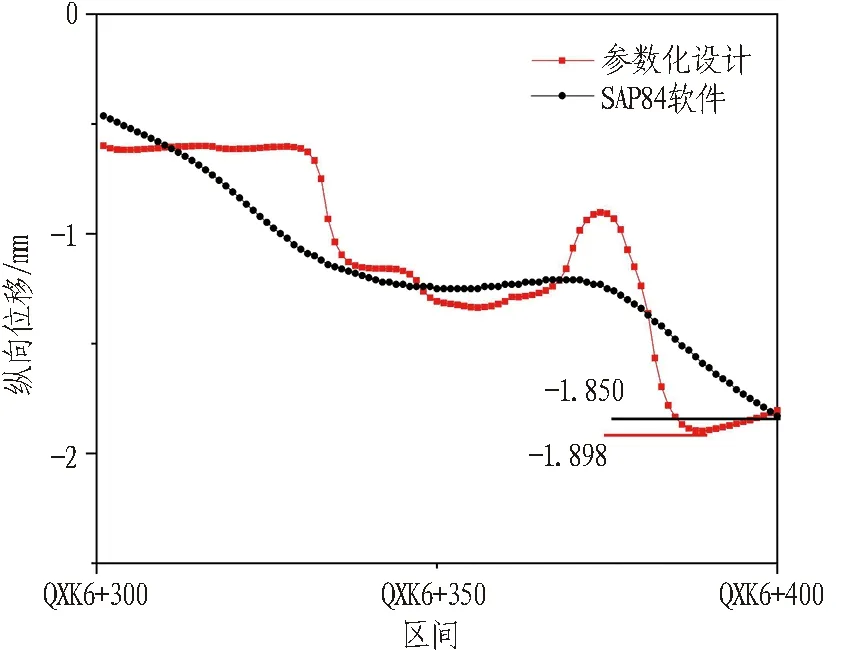
图6 隧道结构的纵向位移比较

根据本方法计算出的结构轴力结果对隧道数字模型进行渲染并输出云图(如图7所示)，每环管片的受压和受拉情况清晰可见，其最大正弯曲应力为0.056 7 MPa。根据等效抗拉刚度，求得最大环缝张开量约为0.154 6 mm，满足规范GB/T 51438—2021[17]对环缝张开量的要求(≤2 mm)。

图7 隧道结构的弯曲应力云图(单位： MPa)

最后，本研究将2种方法的耗时(包括建模与计算过程)进行对比，结果如表2所示。本方法在建模和设定约束条件方面分别可以节省80%和50%以上的耗时；在计算方面，本方法可以在2 s内完成计算。因此，本方法能有效支持后续设计迭代和不同区间的计算需求。

表2 结构计算模型耗时比较

4 结论与讨论

1)本研究提出了利用地质钻孔数据驱动隧道结构计算的思路。该方法在两湖隧道(东湖段)工程设计案例中得到应用，并与现有计算方法的结果进行对比，验证了本方法既能满足盾构隧道纵向结构设计的规范要求，又能与盾构隧道参数化自动建模方法进行衔接，从而提高地下空间工程数字化设计水平。

2)本方法基于钻孔数据与参数化建模能构建更精细的结构模型与荷载布置； 同时，其利用参数化设计方法大大减少了隧道纵向结构设计中的手工建模、人工评估、参数设定等工作量，耗时明显缩短，且后期能支持不同区间的验算需求与优化迭代，显著提升了设计效率。

3)本研究为盾构隧道施工时的结构沉降变形分析提供了工作基础，下一步研究可在盾构施工过程中模拟沿隧道纵向有堆载(或局部地表卸载)的情况，继而开展风险评估以支持盾构施工安全管控。