努森真空泵内部流导的蒙特卡洛模拟
*王范宇 柯杰坤 谭丽萍 卢苇
(广西大学机械工程学院 广西 530004)
微机电系统(MEMS)的兴起要求真空泵逐步向微型化发展,结构简单且无运动部件的努森泵逐渐成为一种具有竞争力的微型真空泵[1]。Vargo and Muntz[2]定性研究了努森泵的运行特性,并且证实了将努森泵用作微尺度和宏观尺度真空泵的可行性。Kugimoto等[3]指出需要多级串并联提高泵送性能。考虑努森真空泵抽速问题,通常采用多个微通道并联或者多孔膜来增加真空泵的抽吸能力。
流导对于真空系统有着重要意义。鉴于努森真空泵内部的微通道中也存在流导,可见其流导性能也是此类真空泵固有的重要参数。王博韬等[4]研究热流逸效应抽真空特性后发现,微通道的流导在很大程度上影响着抽气时间、抽速等性能指标。当前大多运用半经验公式来计算流导,场合不同,修正系数也要随之校正,使得计算结果较复杂且容易受其他因素产生较大影响。故尝试采用蒙特卡洛方法计算流导,或将有助于我们更深入地认识这类真空泵的运行机制,进而为其优化设计及应用提供指导。
1.努森真空泵内部流导的蒙特卡洛模拟建模
(1)模拟对象
图1为努森真空泵的结构示意图,当微通道的特征尺寸与气体分子平均自由程度相当或更小且沿壁面切线方向存在温度梯度时,内壁周围的气体分子会自发地向温度升高的方向进行蠕动,随着流动的发展,热端与冷端形成压差后又产生由热端流向冷端的压力驱动流,这一现象称为热流逸效应。根据该效应,当微通道冷端连接密闭空间而热端连接外界(可以是大气、也可以是另一空间)时,密闭空间内的气体分子会源源不断被抽出,从而使其内的压力不断降低而形成真空。

图1 努森真空泵的结构及热流逸效应
微通道的流导是影响努森真空泵效率的一个重要因素。当热流逸效应发生时,气体流动处于稀薄状态,分子之间的碰撞可以忽略,此时计算相对较为简单。
本文只考虑矩形截面微通道内气流的几何要素,气体的温度和压力等其他非几何要素折合为管口入口流导Cmk处理[5]。这样便能够把几何要素和非几何要素分别研究。矩形微通道管口流导就是气体分子通过微孔的流导,即:

式中,Aa为微通道的截面积,m2;k为玻尔兹曼常数,k=1.380649×10-23J/K;Tavg为微通道的平均温度,K;m为气体分子的质量,kg。
几何要素包括微通道的特征尺寸和气体分子的几何运动。气体分子的流动区域与微通道特征尺寸相关,根据努森数Kn来划分。Kn定义为:

式中,λ为气体分子平均自由程,m;Lr为微通道的特征尺寸,m。
微通道内气体运动达到平衡时两端的压力和温度关系可参考文献[6]。
(2)蒙特卡洛模拟过程
参考图2,入射点为入射面XOZ上的随机一点,对应坐标(x0,0,z0);分子入射遵循余弦定律;μ1、μ2、μ3分别代表分子入射方向向量在X、Y、Z轴上的向量分量;L、W、H分别为微通道截面矩形的长、宽、高;①②③④分别为矩形微通道的4个壁面。
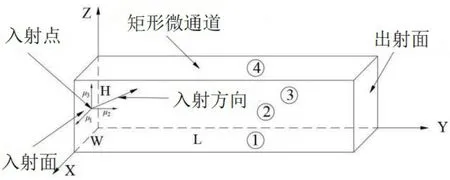
图2 气体分子碰撞模型及其入射参数
对于上述入射参数,建立如下随机数量关系:x0=Wδ1,z0=Hδ2;μ1=sinδ3·cosδ4,μ2=sinδ3·sinδ4,μ3=cosδ3,式中的δi均为[0,1]区间的随机数。再根据x1=x0+α1μ1,y1=y0+α1μ2z1=z0+α1μ3(α1为第一次运动步长)计算出第一次运动后的碰撞点(x1,y1,z1)。如此时y1≥L,则说明未产生碰撞直接从出口面射出。否则,再以此点作为新的入射点,建立新的入射方向向量,模拟一次新的运动,以此类推,直至yi超出[0,1]的区间。
图3为模拟流程,取模拟分子总数N= 100000;n为射出出口面的分子数;k为射入入口面的分子数;Cmk为管口入口的流导,m3/s;Cm为矩形微通道的流导(自由分子流下),m3/s。第一次运动气体分子有4种碰撞情况未从出口面射出,第二次运动及往后均有3种情况,因此经过M次运动每个分子一共有4×3M-1种情况。
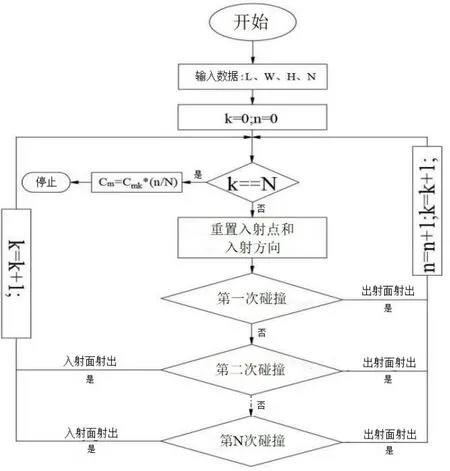
图3 模拟流程
2.微通道流导的模拟结果分析
(1)矩形微通道流导的模拟结果分析
蒙特卡罗模拟仅与微通道的相对尺寸相关。本文取微通道的W为定值,以微通道的L/W和H/W作为变量进行分析。
不同长宽比下矩形微通道高宽比对流导的影响见图4,若L/W一定,随着H/W的增大,矩形微通道的流导也将基本趋于线性增大。例如,当L/W=20时,取H/W=1到10的区间,其流导增长率为4.60×10-24m3/s。此外,随着L/W值越大(即管路越长的时候),流导虽然也会随着H/W增大而增大,但是增长率却越来越小,如在L/W=800时,流导的平均变化率仅为2.45×10-25m3/s。

图4 矩形微通道高宽比对流导的影响
不同高宽比下矩形微通道长度对流导的影响见图5,矩形微通道的流导随L的增大而减小;当L较小时,H/W越大流导越小,但随着L的增大,H/W对流导的影响越小。如以L=20nm为例,当H/W=1、5、100时,其流导分别为5.39×10-23m3/s、5.07×10-23m3/s、9.71×10-24m3/s,取H/W=1为参照,H/W=5和H/W=100时相对于参照的变化率约为-6.02%和-81.99%。若以L=800nm为例,当H/W=1、5、100时,其流导分别为1.91×10-24m3/s、1.84×10-24m3/s、1.17×10-24m3/s,取H/W=1为参照,H/W=5和H/W=100时相对于参照的变化率约为-3.51%和-61.40%。

图5 矩形微通道长度对流导的影响
因此由流导性能作为切入点,增大努森真空泵微通道的截面积能更好地提升流导性能;且在截面积相同的情况下令H/W尽可能接近1,此时短微通道具有显著优势。
(2)不同形状微通道流导的模拟结果对比分析
三种截面形状下微通道长度对流导的影响见图6。可见无论何种截面形状的微通道,流导都随着L的增加而减小且变化率基本一致;圆形截面的流导性能要优于椭圆形和矩形,但随着L的增加截面形状对流导的影响越小。如L=20nm时,矩形和椭圆形微通道的流导与圆形微通道的流导分别相差约1.13×10-23m3/s和1.44×10-23m3/s;而L=800nm时,矩形和椭圆形微通道的流导与圆形微通道的流导分别相差仅约5.70×10-25m3/s和1.40×10-25m3/s。

图6 三种截面形状下微通道长度对流导的影响
因此在设计努森真空泵时,应采用圆形截面微通道。
(3)模拟结果与计算结果对比分析
矩形微通道流导模拟结果与计算结果对比见图7。微通道长度Lx=10-9m时,蒙特卡洛模拟结果与公式计算结果相对误差仅仅为1.31%,但是在微通道长度Lx=3×10-8m时,模拟结果与公式计算结果相对误差为9.58%。这是因为蒙特卡洛模拟是一种概率统计的模拟,这种误差会随着模拟分子数的增加而减小,但模拟无限个分子仅限于理想理论假设,是无法实现的,故本身就会存在固有误差;其次,在短微通道的流导计算中,微通道的管口效应是不可忽略的,且短微通道的流导计算只能用近似方法进行计算,无明确公式。可见两种结果之间还存在一定的误差,但是模拟结果与公式计算结果的趋势基本相同且误差在允许范围之内,因此蒙特卡洛模拟方法用于研究微通道流导是可行的。
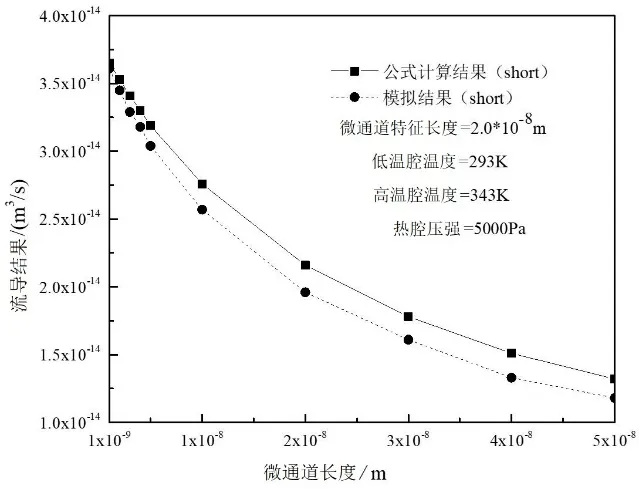
图7 模拟结果与公式计算对比
3.结论
本文研究了矩形微通道高宽比和长度对其流导的影响,比对了三种截面形状流导性能,并验证了蒙特卡洛模拟方法计算微通道流导的可行性。主要结论如下:
(1)长度一定时,流导会随着高宽比的增大而近乎线性增大,但随着长度增大,其变化率越小;高宽比一定时,流导会随着长度的增加而衰减,但随着长度增大,由高宽比对流导产生的影响越来越小;此外,无论何种形状截面的微通道,其长度对流导的影响趋势基本一致;蒙特卡洛模拟结果与公式计算结果还存在一定误差,但变化趋势大体相同。
(2)运用蒙特卡洛模拟方法求微通道流导是可行的;短微通道较长微通道的流导性能更优,增大截面积并尽可能令高宽比等于1可显著提升流导性能;三种截面形状对比下圆形截面微通道的流导性能总是最佳。

