基于耦合纯无网格方法时间分数阶下孤立子波碰撞过程的数值模拟研究*

李 悦，蒋戎戎，蒋 涛

（扬州大学 数学科学学院，江苏 扬州 225002）

（我刊编委赵景军推荐）

引 言

非线性耦合偏微分系统在流体力学、固体物理等领域具有重要的应用价值，其中耦合非线性Schrödinger 系统(CNLS)[1-4]常用来系统描述两个相互作用非线性孤立子波的碰撞过程.近年来，受分数阶算子[5-8]影响的耦合非线性Schrödinger 系统受到广泛关注，其与整数阶情况下的物理现象截然不同，比如受分数阶影响出现了孤立波的塌缩现象[9].

关于分数阶CNLS的数值研究，由于受非线性Schrödinger 方程中非线性项以及分数阶的影响，很难通过解析的手段得到其理论解.因此关于分数阶的数值模拟方法[10-13]成为了重要的研究手段，其中大部分是基于网格类的，如有限元法[10]、有限差分法[11]、无单元Galerkin 法[12]等，这类基于网格的方法在处理局部加密以及非均匀分布时较为复杂，很难实现，而无网格方法[13]能弥补上述缺点，但对无网格方法的研究尤为罕见.

基于上述分析，本文针对TF-CNLS 方程给出一种耦合纯无网格有限点集法(CFPM)[14-15].该方法的基本思想是：首先，基于Caputo 分数阶高精度差分格式对时间分数阶项进行离散；其次，基于Taylor 展开和加权最小二乘思想，并引入双曲余弦核函数对空间项进行离散求解，从而得到一种能够准确数值预测TF-CNLS 方程的CFPM.数值研究结果展示了本文提出的CFPM 能够准确地求解一维TF-CNLS 方程且具有近似二阶收敛精度，并将其数值模拟结果与有限差分结果作对比，表明CFPM 能够有效预测TF-CNLS 方程的孤立子波非弹性碰撞过程波的复杂传播现象.

1 时间分数阶耦合非线性Schrödinger (TF-CNLS)方程

耦合非线性Schrödinger (CNLS)方程[3]常被用来模拟离散保守系统中两个相互作用的非线性波包.本文考虑一维情况下时间分数阶耦合非线性Schrödinger 方程：

初始条件为

边界条件通常为周期边界或如下边界条件：

其中uk(k=1,2)是两个极振中的复值波振幅，i=是虚数单位，η是线性双折射的归一化强度，参数 λ描述了群速度色散，β是跨相位调制.

分数阶导数[16]的定义有很多种，其中Riemann-Liouville 和 Caputo 分数阶导数是近年来最常用的两种分数阶微积分方法，本文主要采用Caputo 分数阶导数.

定义1设 α是一个正实数，令q-1＜α＜q,q为一个正整数.函数f(t)定 义在区间 [a,b]上，其 α阶Caputo 分数阶导数形式为

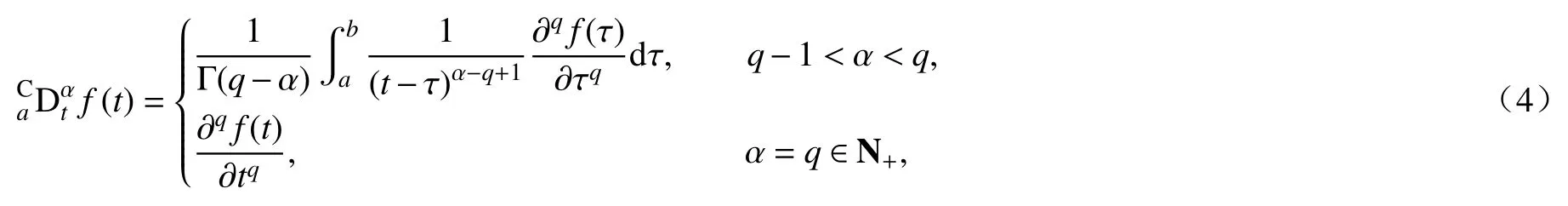
其中t∈[a,b].易知

其中算子 Γ(·)是Gamma 函数，即为广义的阶乘，且允许取非整数及复数值.

2 CFPM 离散格式

本文针对TF-CNLS 方程的模拟研究，基于Caputo 分数阶高精度差分格式与FPM 离散格式进行耦合，给出一种具有较高精度和稳定性的CFPM 来模拟TF-CNLS 方程.其思想是：首先，应用3 -α精度的Caputo 导数形式对时间项进行处理；其次，采用具有较好稳定性的双曲余弦核函数[17]推广应用FPM 对空间导数项进行二阶显式离散.

2.1 基于Caputo 导数时间分数阶离散格式

根据文献[18-19]，目前针对基于Caputo 分数阶导数的差分格式常见的有：“2-α”(L1 型)和“3-α”(L1-2 型).本文采用精度较高的L1-2 型格式，并与显式FPM 耦合求解TF-CNLS 方程.在本小节中，引入时间项误差为O(Δt3-α)的L1-2 型格式.

设tn=nΔt,tn+1/2=(tn+1+tn)/2，其中n=0,1,2,···,Δt是时间步长.定义差商算子：

u(t)∈C1[0,tn](n≥0) α(0＜α＜1)

假设，根据定义可知，对于任意的有

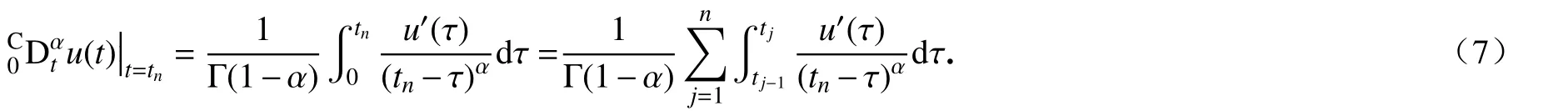
设插值函数Π1,ju(t)=由线性插值理论可知

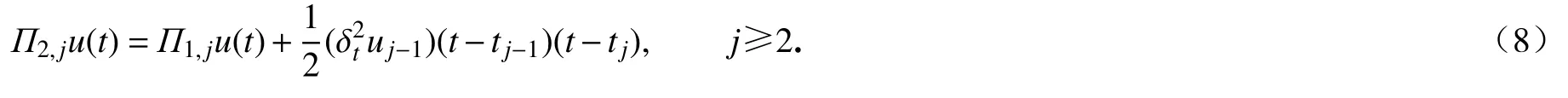
对于函数u(t)，我们可以得到一个新的α (0＜α＜1)阶Caputo 分数阶导数的数值近似，形式如下：

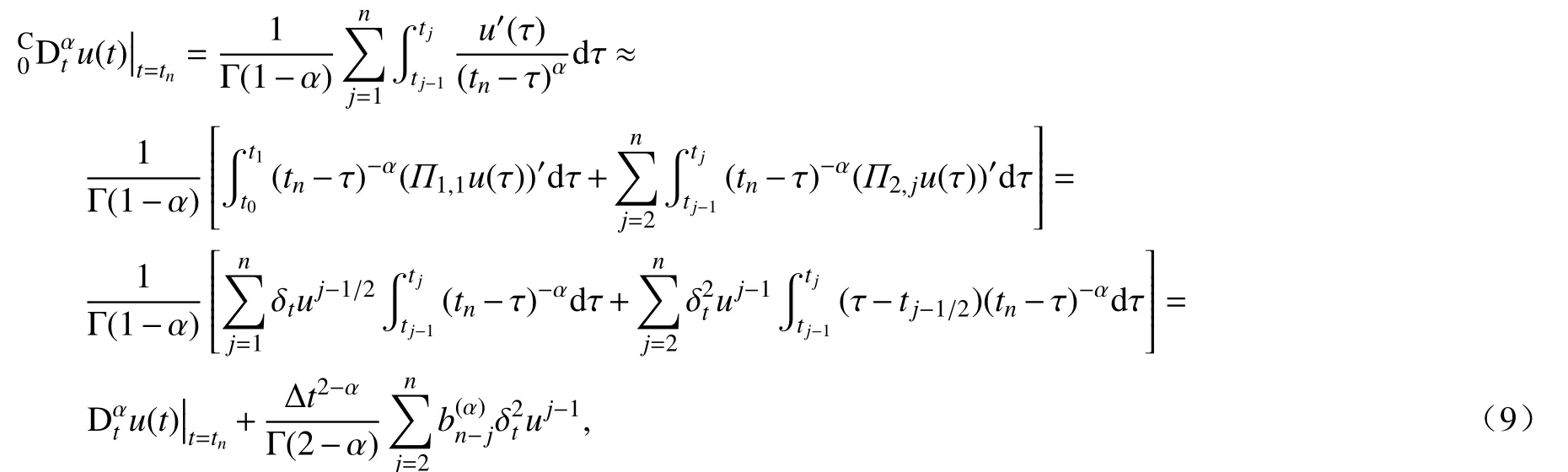
其中系数

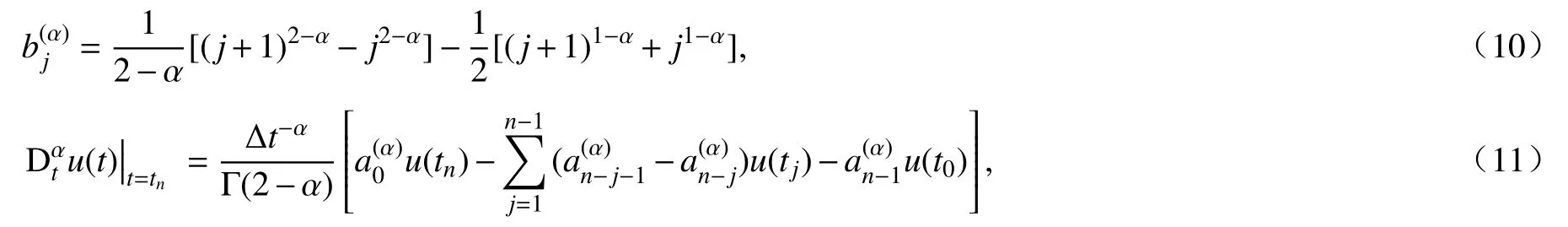
引理1[19]对于任意α (0＜α＜1),设

近似格式(7)可以写成

其中

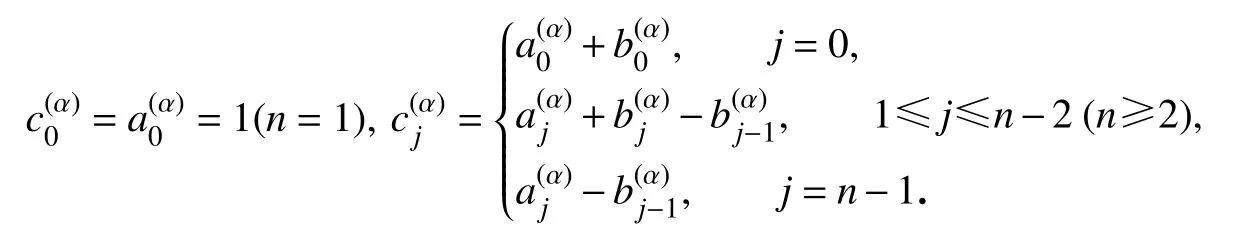
系数{}满足以下性质.

引理2[19]对于任意 α(0＜α＜1)，式(15) 中(0≤j≤n-1,n≥3)，则

2.2 空间导数FPM 离散格式

FPM 常被用来求解方程(1)，直接应用基于Taylor 展开和加权最小二乘思想[18-19]的显式FPM 对一、二阶空间导数项进行离散求解.设未知函数为u(x)，求解区域为Ω ⊂Rd(d=1)，区域内的任意节点为xi(i=1,2,···,N)(N为节点总数)，引入加权最小二乘对函数在x处的一、二阶导数进行离散近似.加权最小二乘中选取双曲余弦核函数[17]，其形式如下：

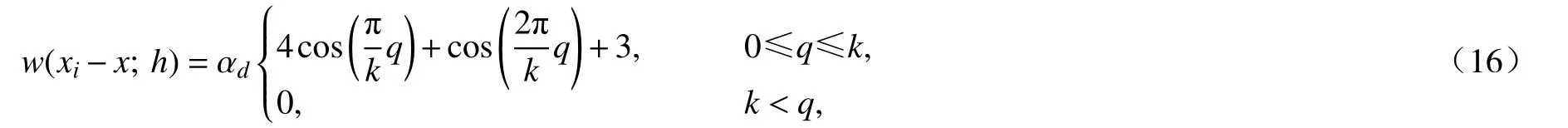
其中q=rij/h,rij=|||xi-xj|||，αd是正常数，一维情况下αd=1/(6kh)，h为光滑长度，此处取h≈0.95×d0(d0为初始距离)，支持域范围是以2.5h为半径的圆.

考虑支持域内相邻节点xi(i=1,2,···,m)在x处Taylor 展开，可得

其中ei是Taylor 展开式的误差余项.式(17)可化为

其中

dxi分别表示xi-x(i=1,2,···,m).

通过误差ei加权最小二乘法对未知函数u的一、二阶导数进行求解，可得

J=(Ma-b)TW(Ma-b)Ww1w2···,wm

式(19)可以写成，其中为对角矩阵，对角线元素为，,.

根据J的极小值原理，得到

式(20)涉及2×2 局部系数矩阵，函数的一、二阶导数值可通过其近似求得.

为保证数值方法的稳定性，本文选取的时间步长 Δt≤0.1d02(d0为节点初始距离)通常满足限制性条件(见文献[15,20]).

由此可得方程(1)的CFPM 离散格式为

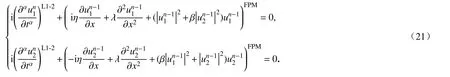
注1在CFPM 离散过程中，空间层采用Taylor 展开以及加权最小二乘思想，其截断误差具有近似二阶精度[14]；时间层采用精度较高的Caputo 分数阶导数L1-2 型格式，具有3 -α阶精度[15].

3 数值收敛性分析

本节采用带解析解的一维二分量时间分数阶非线性Schrödinger 方程，对本文提出的CFPM 求解TFCNLS 方程的数值精度和收敛性进行了分析讨论.

定义均方根误差(ERMS)和收敛阶(Cr)为

其中ui,Ui分别为第i个节点的数值结果和解析解，d1,d2为不同节点的初始间距.

考虑区域Ω=[0,2π]上具有周期边界的非齐次TF-CNLS 方程[21]，对应的方程为

iDαt u(x,t)+iux+uxx+u+v+2(|u|2+|v|2)u=f1(x,t),

iDαt v(x,t)-ivx+vxx+u-v+4(|u|2+|v|2)v=f2(x,t),

初值条件为u(x,0)=0,v(x,0)=0，相应的强制性项为

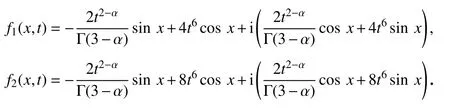
对应该方程的解析解为

u(x,t)=t2(cos(x)+isin(x)),v(x,t)=t2(cos(x)+isin(x)).

通过对算例的模拟，图1和表1～3 体现了本文给出的CFPM 模拟TF-CNLS 方程的数值收敛速度以及灵活可靠性.图1展示了 α=0.7，均匀分布情况下，时间步长为Δt=10-3，不同时刻下CFPM的数值模拟结果，并与解析解作对比，可以看出CFPM的数值模拟结果与解析解一致.表1和表2分别列出了不同α（α=0.9,0.7），t=1.0 时刻不同节点数情况下，三个不同物理量的RMS 误差和收敛阶.从表1和表2可以看出，所给的CFPM 数值模拟TF-CNLS 方程是趋于二阶精度收敛的.

图1 α=0.7，不同时刻下Re(u)，Im(u)的解析解与数值解Fig.1 The exact and numerical solutions of Re(u) and Im(u) with α=0.7 at different moments

表1 α=0.9，t=1.0 时刻下的RMS 误差和收敛阶Table 1 The RMS errors and convergence rates with α=0.9 at t=1.0

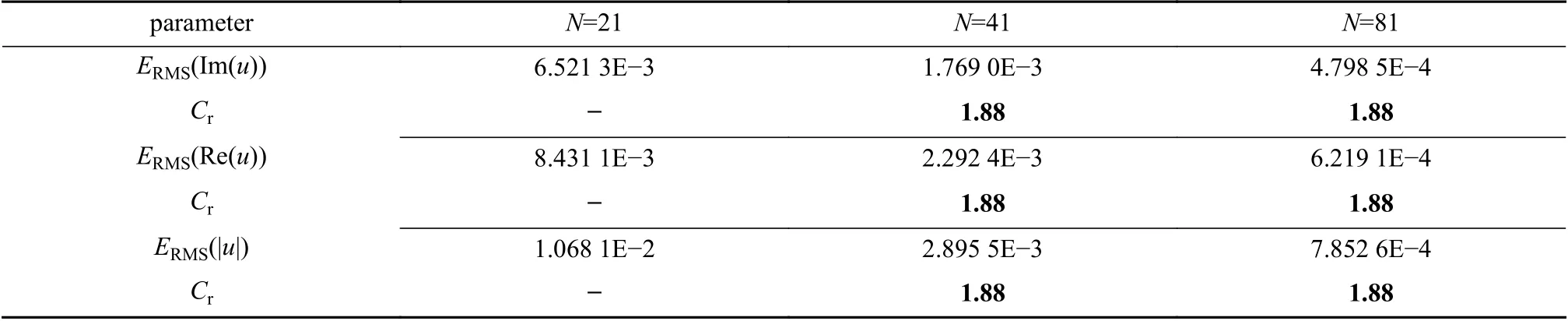
表2 α=0.7，t=1.0 时刻下的RMS 误差和收敛阶Table 2 The RMS errors and convergence rates with α=0.7 at t=1.0

在[0,π/5],[9π/5,2π]处节点局部加密，使得该区域的空间步长为粗节点分布处的一半，其余区域仍采用节点均匀分布方式，时间步长为Δt=10-4，两种分布方式的临界点光滑长度为h≈0.5×(0.95×d1+0.95×d2).表3列出了 α=0.7时，部分时刻下均匀分布与局部加密分布情况下的RMS 误差.由表3可知，节点均匀分布的误差稍大于局部加密时的误差.因此，给出的CFPM 易推广到局部加密情况，具有较好的灵活推广应用性.

表3 α=0.7 时，不同时刻下均匀分布与局部加密情况下的RMS 误差Table 3 The RMS errors of uniform distribution and local refinement with α=0.7 at different moments

4 时间分数阶下孤立波非弹性碰撞过程数值预测

本节主要研究了两种不同边界条件下(周期边界和Dirichlet 边界)，无解析解TF-CNLS 方程描述孤立子波的非弹性碰撞过程，对其进行了数值预测，并与有限差分方法(FDM)进行对比，以验证数值预测的可靠性.所采用的有限差分方法具有二阶精度(详见文献[22]).

4.1 周期边界下TF-CNLS 方程

考虑区域Ω=[-40,40]上的TF-CNLS 方程[2]，其对应的方程为

iDαt u+βuxx+[λ1|u|2+(λ1+2λ2)|v|2]u+γu+Γv=0,

iDαt v+βvxx+[λ1|v|2+(λ1+2λ2)|u|2]v+γv+Γu=0,

初值条件为

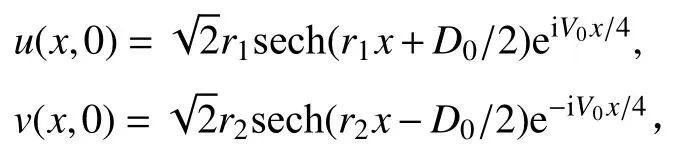
其中系数 β=1,λ1=1,λ2=2,γ=Γ=0，r1=r2=1,D0=20,V0=1.周期边界条件为u(x,t)=u(x+80,t)，v(x,t)=v(x+80,t).

本小节运用CFPM 对该算例进行了数值预测，图2给出了t=30时，不同α下，CFPM 和FDM的数值模拟结果.从图2可以看出，分数阶情况下的孤立子波的峰值减小并变宽，且CFPM 与FDM的数值结果拟合.因此，给出的CFPM 能够准确模拟预测TF-CNLS 方程.

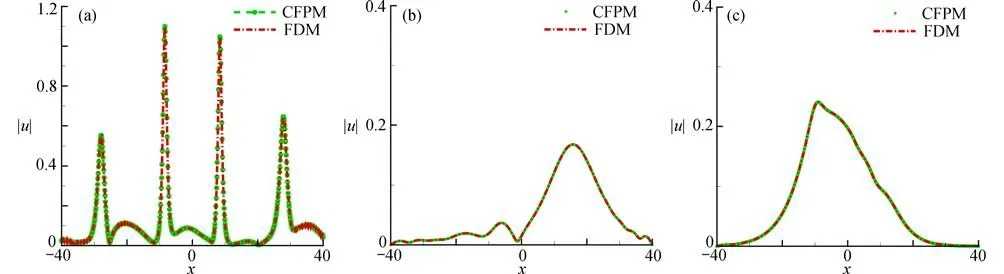
图2 t=30 时孤立波函数|u|的数值结果对比： (a) α=1.0；(b) α=0.9；(c) α=0.7Fig.2 Comparisons of the numerical results of isolated wave function |u| at t=30: (a) α=1.0; (b) α=0.9; (c) α=0.7

图3给出了CFPM的数值模拟结果，时间步长为Δt=10-6，其中图3(a)是整数阶情况下的数值结果，图3(b)、图3(c)分别是α=0.9,α=0.7时的CFPM 数值模拟结果.由图3所有数值结果可以看出，时间整数阶下在碰撞之后出现了四个孤立波，分数阶情况下的孤立子波在非弹性碰撞过程中出现了复杂的传播现象，该现象与文献[9]中波的塌缩现象类似，且与整数阶现象截然不同.

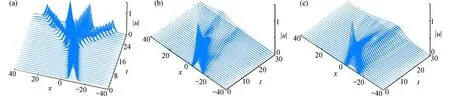
图3 CFPM 对孤立波函数|u|的数值结果：(a) α=1.0；(b) α=0.9；(c) α=0.7Fig.3 Numerical results of the CFPM for isolated wave function |u|: (a) α=1.0; (b) α=0.9; (c) α=0.7

4.2 Dirichlet 边界下TF-CNLS 方程

为体现提出的CFPM 求解带Dirichlet 边界TF-CNLS 方程的准确性，本小节考虑区域Ω=[-40,40]的一维二分量TF-CNLS 方程，其对应的方程[3]为

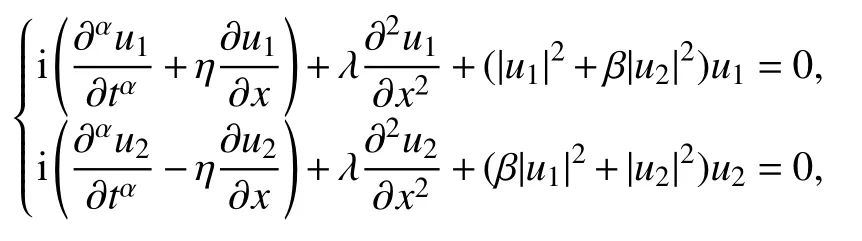
初值条件为

其中 η=0,λ=1,β=2/3,V0=1.3,D0=25,r1=r2=1.

本小节采用提出的方法对该算例进行了数值预测，图4给出了不同α下，t=30时，CFPM 和FDM 对孤立波函数 |u1|的数值模拟结果.从图4可以看出，CFPM 与FDM的数值结果一致，由此表明本文的数值研究是可靠的.

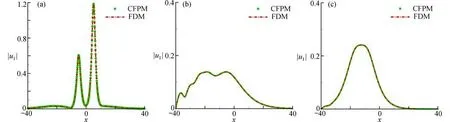
图4 t=30 时刻下，孤立波函数|u1|的数值结果对比： (a) α=1.0；(b) α=0.9；(c) α=0.7Fig.4 Comparisons of the numerical results of isolated wave function |u1| at t=30: (a) α=1.0; (b) α=0.9; (c) α=0.7

图5和图6给出了CFPM的数值模拟结果，时间步长为Δt=10-6，其中图5是不同α 下孤立波函数 |u1|的数值预测结果，图6是不同α下孤立波函数 |u2|的数值预测结果.图5和图6展示了整数阶和时间分数阶TFCNLS 方程的孤立波传播现象，可以看出两种情况下的现象是显然不同的，整数阶下波在碰撞后出现了两个孤立波，而时间分数阶下出现了波的塌缩现象，其现象相较于整数阶更为复杂.

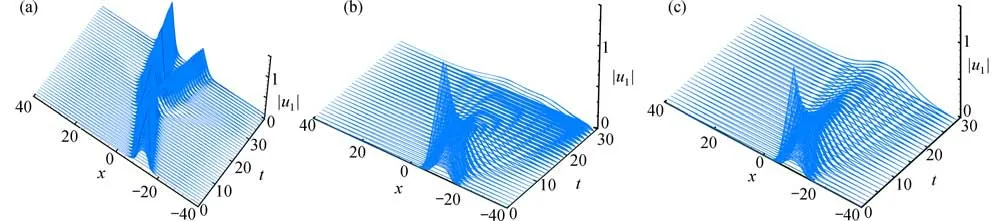
图5 CFPM 对孤立波函数|u1|的数值结果：(a) α=1.0；(b) α=0.9；(c) α=0.7Fig.5 Numerical results of the CFPM for isolated wave function |u1|: (a) α=1.0; (b) α=0.9; (c) α=0.7

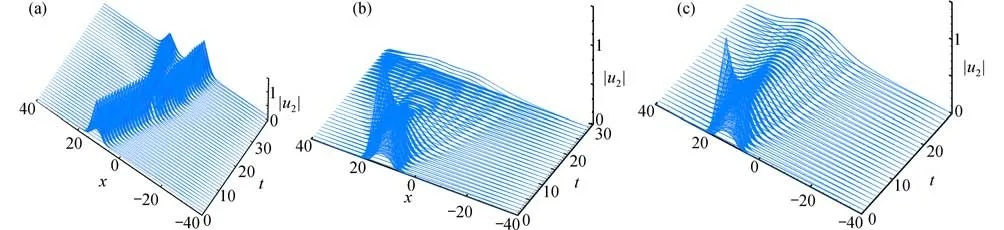
图6 CFPM 对孤立波函数|u2|的数值结果：(a) α=1.0；(b) α=0.9；(c) α=0.7Fig.6 Numerical results of the CFPM for isolated wave function |u2|: (a) α=1.0; (b) α=0.9; (c) α=0.7

由此可见，耦合非线性Schrödinger 方程在时间分数阶下出现了波的塌缩现象，整数阶下出现了多波现象，这两种现象截然不同；且CFPM 模拟预测TF-CNLS 方程的现象与有限差分结果相吻合.因此，给出的CFPM 模拟预测TF-CNLS 方程是准确的.

5 结 论

本文针对时间分数阶耦合非线性Schrödinger 方程的数值预测，首次将Caputo 分数阶导数的一种高精度差分格式和FPM 离散格式进行耦合，提出了一种能够准确预测TF-CNLS 方程下孤立子波非弹性碰撞过程的纯无网格方法(CFPM).数值研究中，首先对提出的CFPM的数值收敛速度进行了验证和分析，并体现了该方法在非均匀分布情况下易实施的优点.然后，对受时间记忆效应影响的孤立子波非弹性碰撞过程进行了数值预测，并与FDM 结果作对比.通过数值模拟可知：

1) 给出的CFPM 对一维TF-CNLS 方程的求解具有近似二阶精度；

2) 对局部加密与均匀分布两种情况下的数值误差进行了讨论，表明所提出的纯无网格方法在区域离散上具有灵活推广应用的优点；

3) CFPM 预测时间分数阶下孤立子波非弹性碰撞过程出现的波塌缩现象与时间整数阶下截然不同，并与FPM 结果比较，表明本文的数值预测结果是可靠的.

因此，本文所提出的CFPM 能够准确、可靠地预测TF-CNLS 方程下孤立子波非弹性碰撞过程中的复杂传播现象，也为时间记忆效应下孤立子波非弹性碰撞过程的纯无网格法模拟提供了依据.