Qplus传感器工艺误差影响的仿真分析*

李 磊, 张明烨, 冷兴龙,3,4, 张凌云, 夏 洋,3,4, 刘 涛,3,4

(1.中国科学院大学,北京 100049； 2.中国科学院微电子研究所,北京 100029； 3.北京市微电子制备仪器设备工程技术研究中心,北京 100176； 4.集成电路测试技术北京市重点实验室,北京 100084)

0 引 言

原子力显微镜(atomic force microscope,AFM)是纳米形貌表面分析的重要工具,基于Qplus传感器的非接触式原子力显微镜(non-contact AFM,NC-AFM)是AFM家族的重要成员[1]。相对于传统NC-AFM中所采用的硅悬臂传感器,基于石英的Qplus传感器的悬臂弹性系数显著提高,使得针尖振幅可以达到亚埃量级,极大提高了AFM的分辨率[2]。Qplus传感器的基本原理是利用单晶石英的压电特性进行自激励、自检测,其相关特性可以通过有限元分析方法求解偏微分方程近似解获得。目前的文献几乎都是对各种石英传感器的理想模型进行分析。例如,Dagdeviren O >E[3]和Higuchi S等人[4]通过有限元分析方法对不同的石英传感器理想模型进行了相应的力学特性分析,Oria R[5]和González L等人[6]通过建立石英传感器的电激励理想仿真模型对石英传感器的机电特性进行了分析。但在实际加工过程中会存在许多工艺误差,例如湿法刻蚀误差、双面光刻对准误差、切向误差等,这些误差会对传感器的结构和性能产生重要影响[7]。

本文采用基于COMSOL的多物理场有限元数值分析方法建立了包含工艺误差的Qplus传感器仿真模型,分析了几种典型的工艺误差对Qplus传感器的本征频率、弹性系数和品质因子等性能指标的影响。仿真结果对传感器设计模型的优化具有指导作用,使制备出的传感器性能参数更接近于预期设计值。

1 模型建立与相关特性求解方法

1.1 Qplus传感器工作原理

早期Qplus传感器的结构类似于将石英音叉的一个臂固定,另一个臂自由振动,后期逐渐发展成一种非对称式的结构[8,9]。相对于石英音叉,Qplus传感器能够避免粘在悬臂上的针尖以及针尖与样品间的相互作用力,破坏两个悬臂的对称性,导致传感器品质因子的降低以及出现其他模态等问题[10]。图1为基于Qplus传感器的AFM探头示意图。通过在电极上施加电激励,利用石英晶体的逆压电效应使悬臂以本征频率振动。同时,利用石英晶体的压电效应产生感应信号。当针尖靠近样品表面时,针尖与样品间的相互作用力会使感应信号发生变化,进而分析出样品表面形貌。

图1 基于Qplus传感器的AFM探头

Qplus传感器的关键性能参数主要有本征频率、品质因子以及弹性系数。对于悬臂宽度为W,厚度为T,长度为L的Qplus传感器,其弹性系数k及本征频率f0可以分别用式(1)、式(2)表示。其中,E和ρ分别为石英单晶的杨氏模量及密度

(1)

(2)

品质因子Q被定义为每个振荡周期的存储能量与损失能量之比,可以通过谐振响应曲线利用式(3)进行求解[11]。其中,f0为传感器的本征频率,Δf为带宽,即谐振曲线的半高宽

Q=f0/Δf

(3)

1.2 Qplus传感器加工工艺误差

图2(a)为采用微纳加工工艺制备出的Qplus传感器,其主要加工工艺有双面光刻、薄膜沉积、湿法刻蚀,具体工艺流程如图2(b)所示。其中,双面光刻工艺需要进行2次,即一次双面光刻(第b3步)及二次双面光刻(第b7步)。其中,一次双面光刻的作用是形成传感器结构的光刻胶图形、二次双面光刻的作用是形成传感器正反面电极的光刻胶图形。由于双面光刻存在一定的对准偏差,因此,双面光刻后会使石英基片正反面光刻胶图形产生错位,从而导致传感器结构及正反面电极发生错位,图2(c1)即为一次双面光刻对准偏差导致的传感器结构错位,使传感器侧壁产生台阶面。第(b8)步工艺石英湿法刻蚀的作用是实现石英基片的图形化,形成Qplus传感器结构。该步工艺误差主要来源于石英晶体各组晶面的腐蚀速率不同导致的刻蚀后石英侧壁出现晶棱,如图2(c2)所示。同时,由于传感器结构复杂,会导致拐角处难以腐蚀干净,如图2(c3)所示。

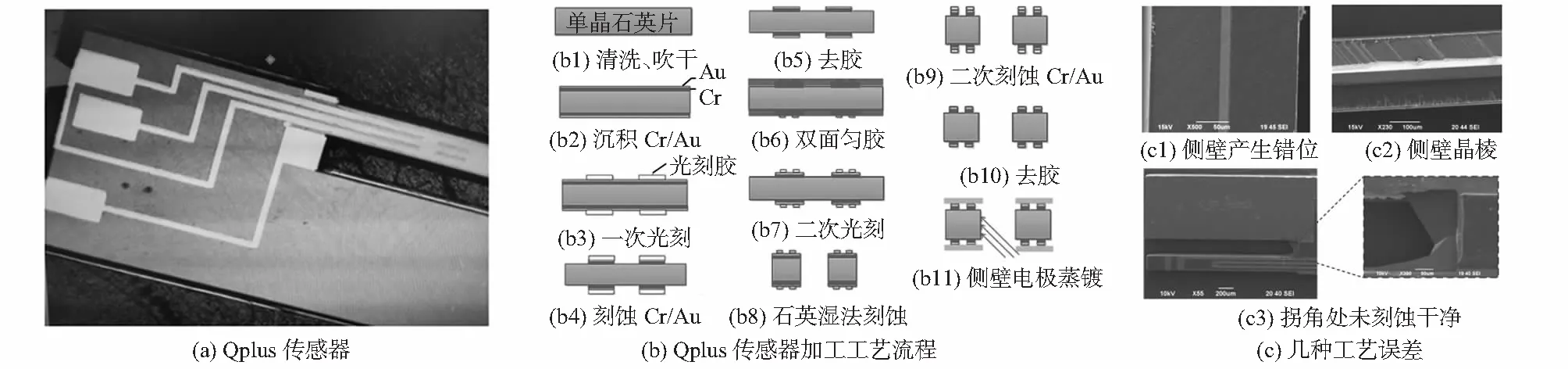
图2 Qplus传感器加工工艺流程及几种工艺误差

1.3 Qplus传感器仿真模型建立

利用COMSOL多物理场仿真平台对Qplus传感器进行建模,图3(a)为Qplus传感器理想模型的几何结构及相关尺寸。采用自由四面体网格对仿真模型进行网格划分,图3(b)为模型网格划分情况,为了提高计算的准确性,在悬臂及电极边界处增加了网格密度。文献[12]中所测量的石英晶体的弹性、压电以及介电系数,添加COMSOL软件材料库中压电模块下的Quartz LH(1978 IEEE)作为传感器模型的材料,材料的密度为2 651 kg/m3,材料的弹性系数如下所示

(4)

材料的压电常数能够反映压电传感器力学及电学特性之间的关系,在COMSOL中用如下耦合矩阵来表示

(5)

图3 模型几何结构、尺寸及网格构建

结合1.2节对Qplus传感器的工艺误差分析,在理想模型的基础上建立包含工艺误差的Qplus传感器仿真模型,如图4、图5所示。图4为根据湿法刻蚀误差建立的仿真模型几何结构,在悬臂两侧构建三菱柱作为刻蚀后侧壁产生的晶棱,同时在拐角处构建四面体作为拐角处的刻蚀残留。图5为根据一次双面光刻误差建立的模型几何结构,将悬臂分割成上下两部分并进行位置平移模拟一次光刻对准偏差导致的结构错位。同理,调整传感器正反面电极的位置模拟二次光刻对准偏差导致的正反面电极错位。

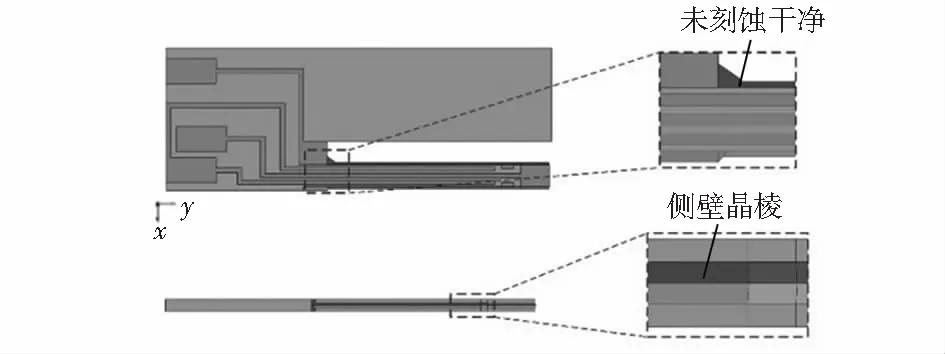
图4 刻蚀误差模型几何结构

图5 一次双面光刻误差模型几何结构

1.4 Qplus传感器相关特性求解方法

Qplus传感器相关特性的求解包括本征频率、弹性系数、品质因子三个方面。其中,传感器本征频率的求解是通过对仿真模型进行特征频率研究得到。弹性系数是通过公式k=F/Δx计算得到,其中,F为在固体力学物理场中对传感器悬臂顶端施加的边载荷,Δx为对模型进行稳态研究得到悬臂顶端的位移。品质因子的求解是通过在电路物理场中对传感器施加电激励,利用自适应频率扫描研究得到电流谐振响应曲线根据式(3)求解得到。其中,电路物理场中的电路组成如图6所示。

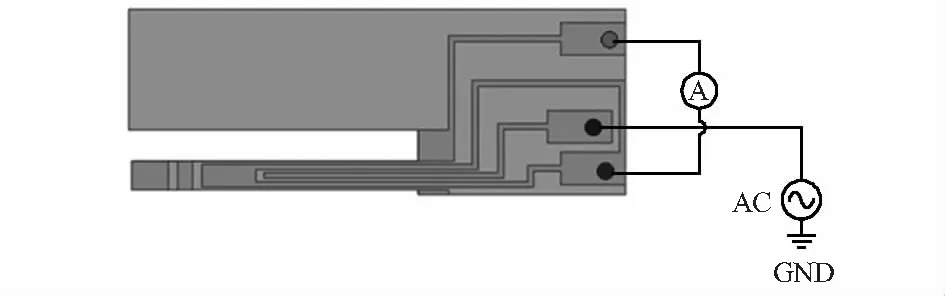
图6 传感器激励检测电路

2 仿真结果分析

2.1 理想设计模型特性求解

采用1.4节所述传感器特性求解方法对理想设计模型相关特性进行求解,图7为求解得到的Qplus传感器理想设计模型的四种不同相邻振动模态及其所对应的本征频率。其中,第二种振动模态(图7(b))为Qplus传感器在AFM中工作时所需要的振动模态,其本征频率为30 698 Hz。图8(a)为悬臂自由端在x方向上的位移大小随力F的变化关系,其斜率的倒数即为传感器的弹性系数,能够求得传感器弹性系数k为1 602 N/m。图8(b)为仿真计算出的感应电流谐振响应曲线,当频率达到30 698 Hz,即传感器本征频率时,感应电流达到最大。该谐振响应曲线半高宽为2.13,根据式(3),可以求得传感器的品质因子为14 412。

图7 Qplus传感器振动模态

图8 悬臂自由端位移随力F变化及仿真计算谐振响应曲线

表1为仿真求解结果与相同结构尺寸的S1.0B型Qplus传感器的实测值[10]对比,其中,二者的品质因子均是在真空环境下计算与测量。由于传感器制备过程中的工艺误差,实际制备出的传感器的弹性系数及本征频率高于理想模型的仿真结果,下文将对工艺误差对传感器性能的影响进行分析。

表1 理想模型仿真值与实测值对比

2.2 湿法刻蚀工艺误差仿真分析

对1.3节所建立的刻蚀误差仿真模型进行数值求解,得到不同误差下传感器的本征频率、弹性系数及品质因子分别如图9及表2所示。由1.2节可知,湿法刻蚀后侧壁产生的晶棱会使传感器悬臂的宽度增大,根据式(1)、式(2)可知,悬臂宽度的增大会导致传感器弹性系数及本征频率的上升。从图9(a)中能够看出,弹性系数随着侧壁晶棱宽度的增大具有明显的上升趋势,且上升幅度逐渐增大,随着晶棱宽度从0增大到50 μm,传感器的弹性系数增大1 200 N/m。图9(b)的结果表明,本征频率随着侧壁晶棱的增大近似呈线性增大,斜率约为119。表2中的结果表明,侧壁晶棱的存在对传感器的品质因子影响较小,随着侧壁晶棱宽度的增加,传感器的品质因子变化幅度在9 %以内。表3为晶棱宽度20 μm时的仿真值与相同结构尺寸的S1.0B型Qplus传感器的实测值对比,二者相对误差仅为3.7 %,体现了仿真方法的有效性及仿真结果的准确性。

图9 晶棱宽度对传感器弹性系数、本征频率的影响

表2 不同晶棱宽度下的传感器品质因子

表3 晶棱宽度20 μm时仿真值与实测值对比

2.3 双面光刻工艺误差仿真分析

对一次双面光刻及二次双面光刻误差仿真模型进行求解得到不同误差下传感器的本征频率、弹性系数及品质因子分别如图10、图11及表4所示。

图10 不同对准偏差对传感器本征频率影响

图11 不同对准偏差对传感器弹性系数影响

表4 不同对准偏差下的传感器品质因子

一次光刻的对准偏差会使刻蚀后传感器结构产生错位,侧壁产生台阶面,导致传感器悬臂整体宽度的增加。二次双面光刻的对准偏差主要是造成传感器正反面电极的错位。图10、图11的结果表明：1)传感器的本征频率及弹性系数与一次双面光刻对准偏差近似呈线性关系,随着对准偏差的增大,本征频率及弹性系数逐渐升高；2)随着二次双面光刻对准偏差的改变,传感器的本征频率及弹性系数没有发生明显变化,变化幅度分别在0.005 %和1.1 %范围内。另外,从表4中能够看出,品质因子受一次及二次双面光刻对准偏差影响均较小,随着对准偏差的增大,变化幅度分别在3.8 %和3.4 %以内。

3 结 论

本文采用基于COMSOL Multiphysics的多物理场有限元数值分析方法,将Qplus传感器加工工艺中的湿法刻蚀及双面光刻工艺所带来的工艺误差引入到了Qplus传感器的仿真模型中,评估了上述工艺误差对Qplus传感器性能参数的影响。结果表明：湿法刻蚀后悬臂侧壁所产生的晶棱会使Qplus传感器的本征频率及弹性系数明显提高,一次双面光刻对准偏差也会导致传感器的弹性系数及本征频率具有一定的提升。因此,在实际设计过程中,可以通过增大悬臂长度、减小悬臂宽度、降低传感器的弹性系数及本征频率,从而减小加工出的传感器性能指标与预期设计值的偏差。除此之外,传感器的品质因子受上述工艺误差影响较小,整体变化幅度在10 %以内。仿真结果有助于理解工艺中的关键因素,为传感器的设计优化提供参考。此外,本文也可以对其它基于石英的MEMS传感器的仿真设计提供借鉴。