基于BDS/GPS融合的精密单点定位解算策略与实测精度

张 怀，聂兆生*，刘 刚，熊 维，刘格格，黄健德，王东振，倪乙鹏

(1. 中国地震局地震研究所,湖北 武汉 430071; 2. 武汉大学 测绘学院, 湖北 武汉 430079)

0 引 言

GNSS精密单点定位(Precise Point Position,PPP)技术采用单台全球卫星导航系统(Global Navigation Satellite System,GNSS)接收机，利用国际GNSS服务组织(International GNSS Service,IGS)提供的精密星历和卫星钟差可实现毫米级到分米级定位精度，具有无需设置地面基准站、机动灵活、可单机作业、定位不受距离限制等特点，在高精度定位导航、地震大地测量学和地球板块运动与动力学研究等方面具有突出优势。全球定位系统(Global Positioning System,GPS)用于导航定位的技术已非常成熟，但是观测条件较差时其定位精度和卫星可用性均有所下降，无法满足需求。2020年，北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)全面组网完成，该系统是中国自主建设运行的全球卫星导航系统。目前，北斗卫星导航系统在轨卫星45颗，包括北斗二号卫星15颗，北斗三号卫星30颗，可为全球用户提供高精度定位、导航和授时服务。国内外学者利用多系统实验(Multi-GNSS Experiment,MGEX)跟踪站数据，分析了BDS、GPS等系统精密单点定位性能，得出BDS/GPS双系统可提高可视卫星数,从而改善卫星的空间几何分布、提高定位精度、增强结果稳定性的结论。

中国地震地质灾害频发，西南地区更是地震地质灾害的重灾区，近几年破坏性较大的地震地质灾害中超过2/3发生在该地区。四川石棉地区位于川滇菱形块体东部边界中段，是鲜水河断裂、安宁河断裂、小金河断裂、大凉山断裂等多条断裂汇聚的“三岔口”，贡嘎山在此隆起至7 500 m，大渡河流经该处最低不足1 000 m，地形起伏剧烈，高差巨大。中国地震局地震研究所在石棉地区布设了GNSS地壳形变监测网，用于研究鲜水河断裂的震间构造变形。受限于交通和地形，观测网主要布设在近EW向峡谷中，SN向遮挡比较严重，大部分流动测站的BDS可视卫星数远多于GPS。

此前研究大多基于MGEX跟踪站数据，模拟较差的观测条件，且GPS可视卫星数与BDS相当，与四川石棉地区实际观测情况相差较大，针对实际观测环境下的单系统与多系统精密单点定位精度及可靠性有待进一步研究。基于此，本文基于四川石棉地区GNSS地壳形变监测网实测数据，利用GREAT程序进行精密单点定位的静态、动态解算，评估BDS、GPS单系统和BDS/GPS双系统在实际恶劣观测环境下的定位精度、收敛速度、稳定性、历元利用率和几何精度衰减因子(GDOP)等。

1 BDS/GPS解算方法及实验方案

1.1 时空基准统一

GPS与BDS的时间系统和坐标系统存在一定的差异。其中，GPS时间是GPS进行定位导航的时间基准，秒长与原子时相同，不闰秒，起始历元是协调世界时(UTC)1980年1月6日0时，GPS时间与UTC的时刻相一致，之后随着时间的积累，GPS时间与UTC的差异为秒的整倍数。UTC最近一次闰秒是在2016年12月31日23点59分59秒，闰秒后GPS时间与UTC之间累积的差异已达到18 s。其表达式为

=+18 s

(1)

式中：为GPS时间；为协调世界时。

BDS的时间基准为北斗时。北斗时采用国际单位制(SI)秒为基本单位连续累计，不闰秒。起始历元为UTC 2006年1月1日00时00分00秒。北斗时通过UTC(NTSC)与国际UTC建立联系，北斗时与国际UTC的偏差保持在50 ns以内。因此，北斗时与GPS时间的秒级偏差约为18 s。其表达式为

=-18 s

(2)

式中：为北斗时。

GPS坐标系统采用WGS-84，BDS采用中国2000大地坐标系(CGCS2000)。两坐标系统所定义的原点、尺度、定向及定向演变的尺度均相同，均对准于国际地球参考框架(ITRF2014)。WGS-84优化后的精度可以达到2 cm，与ITRF2014精度相差无几，而CGCS2000与ITRF2014的一致性约为5 cm，因此，WGS-84和CGCS2000的差异在厘米级。对于导航定位来说，WGS-84和CGCS2000坐标系统被认为是相容一致的，无需进行转换。

1.2 BDS/GPS融合算法

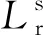
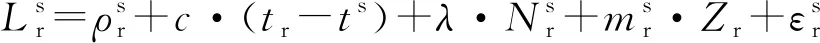
(3)

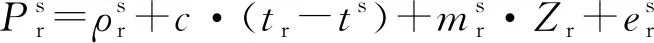
(4)

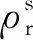
为了削弱电离层对定位精度的影响，本文使用双频无电离层线性组合观测值来消除电离层延迟一阶项影响。考虑到BDS、GPS两系统之间的时间偏差和频间偏差，可得到BDS/GPS双系统无电离层相位和伪距组合模型。其表达式为

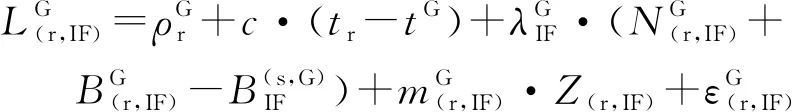
(5)

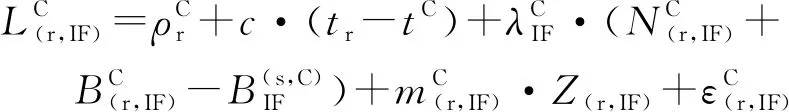
(6)

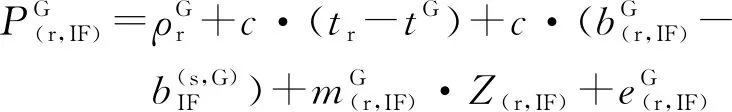
(7)

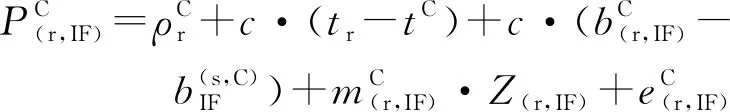
(8)

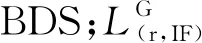
为了充分阐述BDS在BDS/GPS双系统精密单点定位中的作用，本文将BDS、GPS两系统观测值的权重设为等权。对于不同卫星观测值定权，本文采用较为常用的高度角定权模型，将观测值精度()表达为以高度角为变量的函数。具体随机模型为

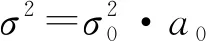
(9)

(10)

式中：为观测值的先验精度；与高度角相关，即高度角小于30°时观测值权重降低，大于等于30°时则等权。

1.3 实验数据及方案

针对四川石棉地区观测环境较为复杂的实际情况，探究在复杂实际观测环境中不同定位模式的定位精度，本文选取石棉地区GNSS监测网中10个流动测站为实验对象(图1)，选取2021年DOY 107、DOY 108两天的流动测站观测数据为处理资料，采样间隔为30 s。所有流动测站均配备了Trimble NetR9 GNSS接收机，可以同时接收BDS B1/B2和GPS L1/L2双频数据。

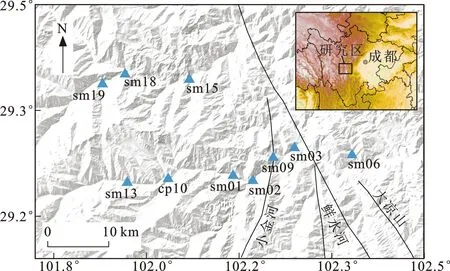
图1 四川石棉地区流动测站位置分布Fig.1 Location Distribution of Station in Shimian Area of Sichuan

利用GREAT程序对每个流动测站进行BDS、GPS单系统以及BDS/GPS双系统精密单点定位的静态解算和动态解算。将DOY 107、DOY 108两天的单日解平均值作为参考值，对比分析每个流动测站0.5、1、2、4、8、12、18、24 h等8个时段的精密单点定位结果。另外，模拟更加恶劣观测环境将高度截止角分别设为10°、20°、30°和40°，分析不同高度角下3种定位模式的定位性能。

2 结果分析

本文基于GNSS地震监测网流动测站观测数据，分别进行了精密单点定位的静态解算和动态解算。GNSS地壳形变监测一般分为地壳长周期形变监测、地震发生前后的地表同震位移观测、地震发生时地壳三维坐标随时间的变化监测以及地震预警中的连续测站位置实时监测。在地壳长周期形变监测和地震发生前后的地表同震位移观测中，由于地壳处于相对稳定状态，所需监测精度较高，一般需要达到毫米级；而在地震发生时，地壳随时间发生较剧烈的位移变化，需要对地表位移变化进行动态监测，监测精度一般需达到厘米级。

静态解算一般用于周期性监测地表位置的长周期运动变化以及当发生地震后利用静态解算获取因地震导致的地表位移。动态解算一般用于分析地震发生时地表位移随时间的变化以及地震预警中地表位置实时监测，以便从中提取地震波到时、水平峰值位移等信息。

2.1 精密单点定位的静态解算

对10个流动测站进行精密单点定位的静态解算，所有流动测站定位精度、可视卫星数以及几何精度衰减因子如图2、3所示。从图2可以看出：BDS单系统在水平方向上大部分流动测站精度优于1.5 cm，垂直方向优于7 cm；GPS单系统在水平方向精度优于1 cm，垂直方向优于5 cm；BDS/GPS双系统精度最高，水平方向优于0.5 cm，垂直方向大部分流动测站优于1 cm。由图3可以看出，单系统可视卫星数较少，几何精度衰减因子偏大，表明流动测站实际观测环境较差。BDS/GPS双系统可有效解决单系统可视卫星数较少的问题，保证有充足的卫星参与解算，并可改善卫星空间几何结构，提高定位精度。BDS单系统精度相比GPS单系统要差的主要原因有两方面：其一，目前BDS跟踪站数量分布不均、数量较少，导致由此计算得到的BDS卫星精密星历和精密钟差精度比GPS低；其二，目前BDS卫星没有提供精确的天线相位中心偏移(PCO)和天线相位中心变化(PCV)改正信息，在解算过程中带入了噪声，导致BDS定位精度比GPS稍差。

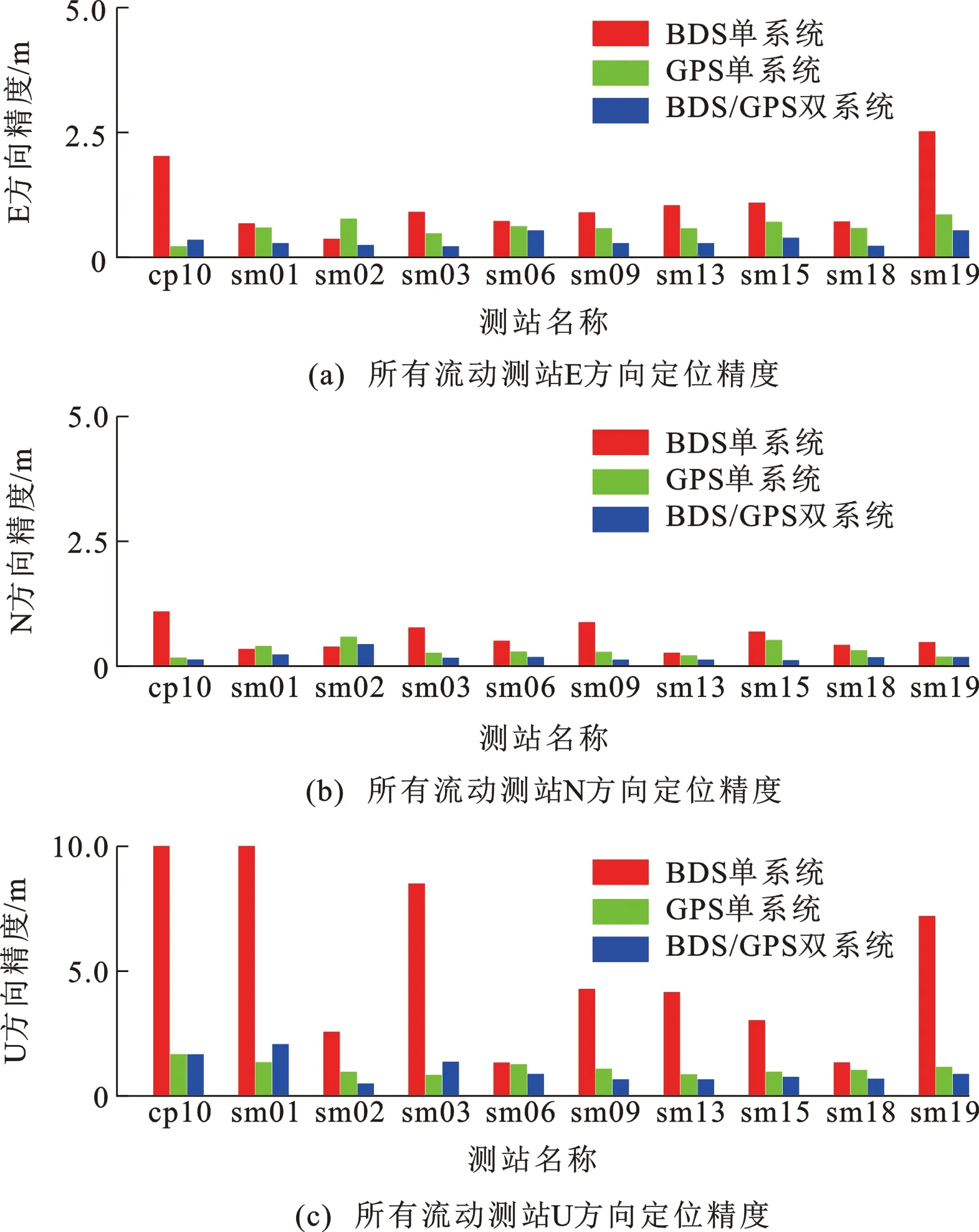
图2 3种定位模式下所有流动测站静态精密单点定位精度Fig.2 Static PPP Positioning Accuracies of All Stations Under Three Positioning Modes

图3 3种定位模式下所有流动测站平均可视卫星数和几何精度衰减因子Fig.3 Average Number of Visible Satellite and GDOP of All Stations Under Three Positioning Modes

为进一步分析3种定位模式的定位收敛速度，本文统计了所有流动测站不同时段长度(0.5、1、2、4、8、12、18、24 h)下BDS、GPS单系统和BDS/GPS双系统的平均定位精度(图4)。由图4可知，GPS单系统的收敛速度要比BDS单系统快，GPS单系统经过约1 h的水平方向定位精度可收敛至10 cm以内，而BDS单系统达到相同精度需要2 h左右；GPS单系统经过2 h的水平方向定位精度可收敛至5 cm以内，而BDS单系统达到相同精度需要约4 h。BDS/GPS双系统收敛速度最快，经过约20 min收敛，E、N、U等3个方向精度即可收敛至10 cm以内，经过约60 min精度即可达到5 cm以内。BDS/GPS双系统可有效缩短收敛时间，相对于BDS和GPS单系统，BDS/GPS双系统收敛到10 cm以内的时间分别减少了83%、80%，收敛到5 cm以内的时间分别减少了75%、50%。

图4 2021年DOY 108所有流动测站不同时段静态精密单点定位平均精度Fig.4 Static PPP Average Positioning Accuracies of All Stations in Different Time on DOY 108, 2021

为评估3种定位模式在更加恶劣环境中的定位性能，以期满足各种工作环境需求，本文进一步将高度截止角分别设为10°、20°、30°、40°进行精密单点定位的静态解算。以sm02测站为例，图5给出了该流动测站DOY 108的BDS、GPS单系统以及BDS/GPS双系统的卫星星空图。BDS、GPS单系统以及BDS/GPS双系统24 h分时段平均定位精度如图6所示。每个流动测站详细解算数据统计结果见表1。从图5可知：卫星星空图在近EW向可视卫星数较多，与图1所示观测环境相一致；与BDS、GPS单系统相比，BDS/GPS双系统可显著改善卫星空间几何结构。

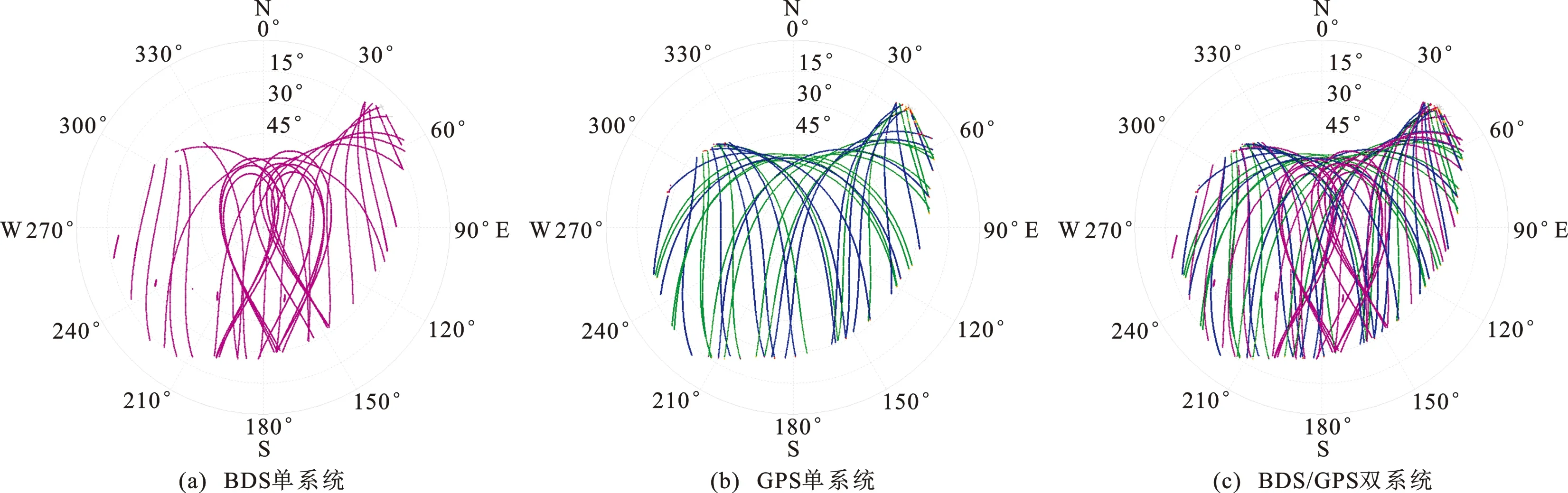
图5 sm02测站3种定位模式下的卫星星空图Fig.5 Skyplots for Station sm02 Under Three Positioning Modes

结合图5、6及表1可知：随着高度角不断增高，GPS历元数和可视卫星数减少，几何精度衰减因子急剧增加，定位精度显著降低；BDS历元数基本保持不变，可视卫星数减少，几何精度衰减因子增加，精度降低；BDS/GPS双系统大大增加了可视卫星数，即使在40°高度角时历元利用率仍为100%，可视卫星数保持在12颗左右，几何精度衰减因子有所增加，但仍保持较低值，其定位精度和收敛速度都明显优于单系统。

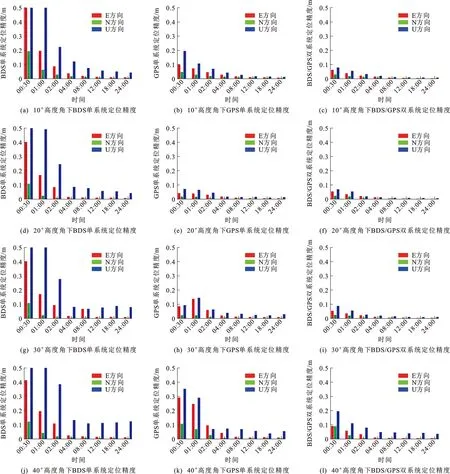
图6 BDS、GPS单系统及BDS/GPS双系统在不同高度角下的静态精密单点定位精度Fig.6 Static PPP Positioning Accuracies of BDS, GPS and BDS/GPS at Different Altitude Angles

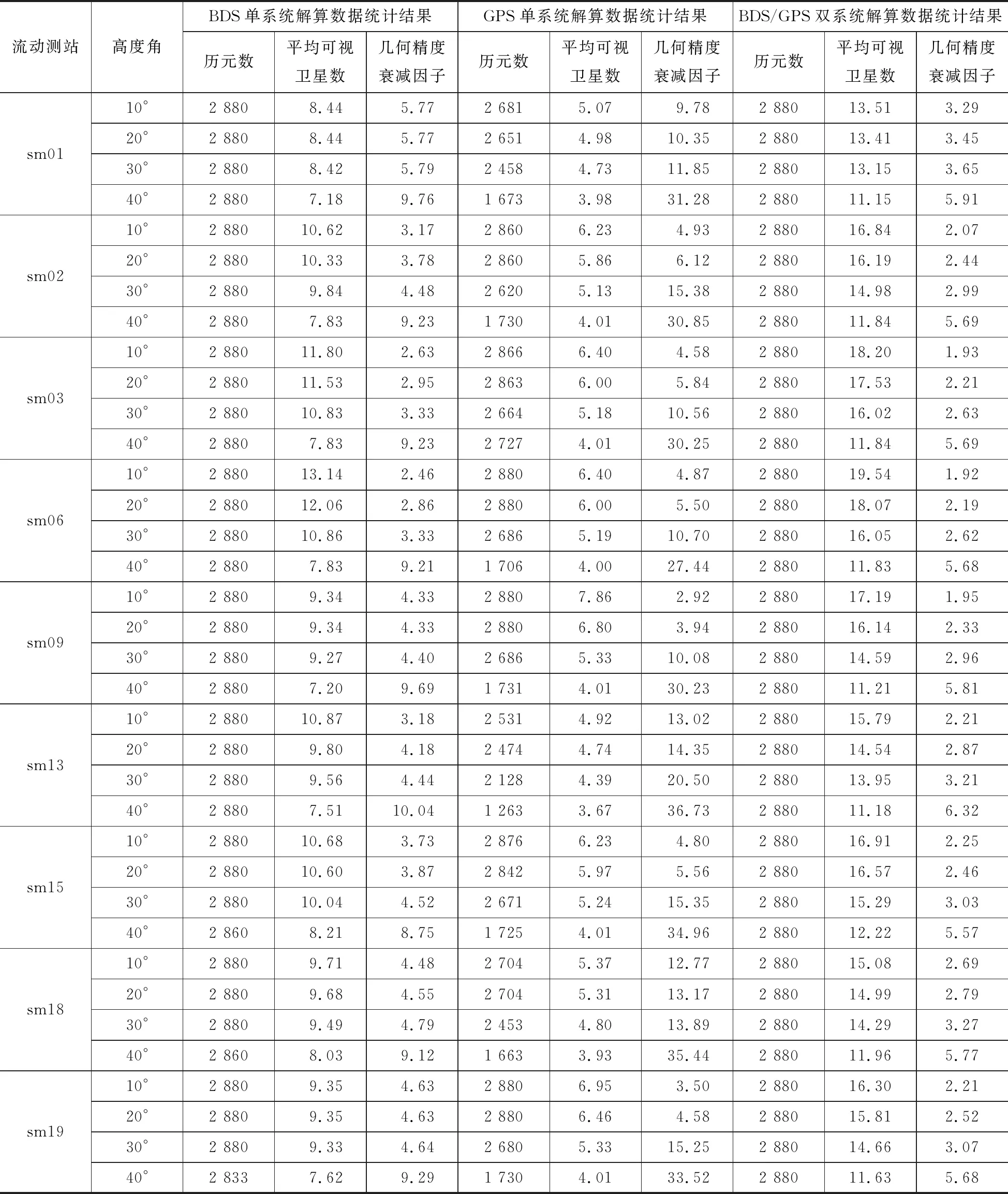
表1 所有流动测站不同高度角下解算数据统计结果

2.2 精密单点定位的动态解算

使用与静态解算相同的处理策略和实验数据进行精密单点定位的动态解算，评估在实际较差观测环境下BDS、GPS单系统和BDS/GPS双系统动态定位性能。所有流动测站动态解算结果如图7所示。从图7可以看出：GPS单系统在E、N、U等3个方向的平均定位精度为0.119、0.150、0.322 m，多个流动测站水平方向定位精度超过0.2 m；BDS单系统在E、N、U等3个方向的平均定位精度为0.019、0.014、0.069 m；BDS/GPS双系统在E、N、U等3个方向的平均定位精度为0.022、0.022、0.086 m，平均精度比BDS单系统低，这是由于GPS单系统精度过低，降低了BDS/GPS双系统精度。

以sm02测站为例，图8给出了BDS、GPS单系统以及BDS/GPS双系统等3种定位模式在不同高度角下精密单点定位的动态解算结果以及高度角为10°时的GPS单系统可视卫星数。从图8可以看出：随着高度角的增加，BDS、GPS单系统定位精度和稳定性逐渐降低，发生定位中断时间和频率也有所增加，且GPS单系统定位精度及稳定性随高度角变化更明显；BDS/GPS双系统精密单点定位的动态解算定位精度和稳定性与GPS单系统相比显著提高，且受高度角影响较小。在山区GNSS地壳形变监测观测环境较差时，通过BDS/GPS双系统融合可弥补单系统存在的缺陷，保证较高的可视卫星数以及定位连续性，显著提高定位性能。BDS/GPS双系统精密单点定位的动态解算抗差力更强，在地震同震形变监测、地震预警等应用中更具优势。

从图3可知，DOY 108的GPS可视卫星数最低为4颗，并没有低于4颗的情况，但是在精密单点定位的动态解算时出现了定位中断。为此，本文分析了所有流动测站BDS、GPS观测数据质量(表2)，发现GPS在某些时段只能接收到单频观测值，MP1值、MP2值为测距码的多路径误差。图8(k)给出了接收到GPS单频观测值的时刻以及该时刻的可视卫星数，定位中断的时刻均是接收到单频观测值的时刻，且该时刻可视卫星数较少。此外，全天都有可能接收到单频观测值，当观测条件较差时，接收到单频观测值会严重影响定位结果。因此，为保证定位精度及定位连续性，可视卫星数最好有6颗或6颗以上，BDS/GPS双系统可显著提高可视卫星数，保持较高的定位精度及稳定性。

根据表2可知，在四川石棉地区特殊观测环境下(在近EW向的狭长山沟中，SN向遮挡相对较严重)，GPS较BDS存在更多的周跳、卫星失锁和信号丢失，且GPS多路径误差更大。频繁的卫星失锁和信号丢失会导致观测弧段不连续，导致模糊度解算不准确产生系统性粗差，从而影响精密单点定位的动态解算精度。此外，大量周跳和较大的多路径误差也会对定位精度产生负面影响。单频观测值、周跳、卫星失锁以及信号丢失这些因素共同导致了GPS精密单点定位的动态解算精度降低。

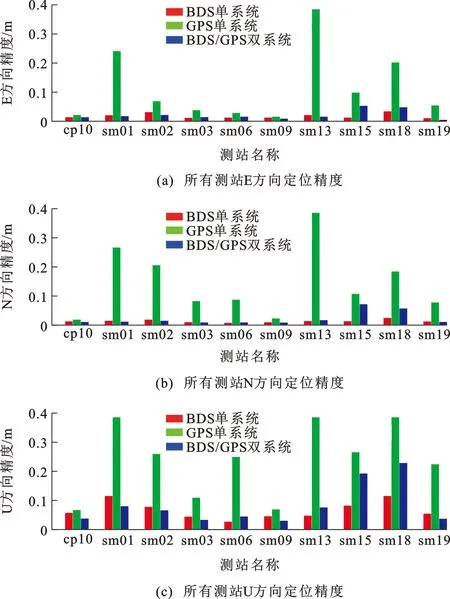
图7 BDS、GPS单系统和BDS/GPS双系统动态精密单点定位精度Fig.7 Dynamic PPP Positioning Accuracies of BDS, GPS and BDS/GPS

3 结 语

本文针对实际GNSS地壳形变流动观测中遇到的观测环境较差、GPS可视卫星数较少等问题，提出采用BDS/GPS双系统进行观测。利用GREAT程序进行精密单点定位解算，对比分析其定位精度、收敛速度以及数据质量。

在峡谷特殊环境下，BDS/GPS双系统精密单点定位的静态解算精度在水平方向优于0.5 cm，垂直方向大部分流动测站优于1 cm；精密单点定位的动态解算精度在水平方向优于2.5 cm，垂直方向优于9 cm，可满足地壳长周期及震时形变监测精度需求。BDS/GPS双系统与BDS、GPS单系统相比，静态定位性能显著提高，定位精度可提高20%～50%，收敛速度可提高50%～80%；BDS/GPS双系统可大大增加可视卫星数，改善卫星空间几何结构，降低几何精度衰减因子，保持较高的历元利用率。因此，在高差较大、地形起伏剧烈等复杂观测环境中，BDS单系统可在地壳形变监测中发挥重要作用，BDS/GPS双系统因其优越的定位性能具有更好的应用价值。

改变高度角模拟更加恶劣的观测环境，发现单系统定位性能急剧降低，多系统则保持较高精度，稳定性较强。随着高度角升高，GPS单系统定位精度降低，几何精度衰减因子显著增高，历元利用率急剧降低。BDS/GPS双系统稳定性较强，在40°高度角时，历元利用率仍为100%，可视卫星数保持在12颗左右。BDS/GPS双系统可消除单系统在精密单点定位的动态解算中由双频观测值缺失导致的定位中断，显著提高定位精度和稳定性，表明BDS/GPS双系统精密单点定位的动态解算在地壳形变监测以及强震预警等方面的应用更具优势。

表2 GPS与BDS观测数据质量统计结果

在精密单点定位的动态解算方面，观测条件受限导致GPS观测值中包含更多的卫星失锁、信号丢失和周跳以及较大的多路径误差，可能导致GPS动态解算过程中包含了粗差。此外，接收单频观测值会降低可视卫星数，从而严重影响定位性能，因此，可视卫星数需有6颗或6颗以上才能保证连续动态的精密单点定位。BDS/GPS双系统融合解算可以大大提高可视卫星数，保持较高历元利用率，有效解决观测条件较差时可视卫星数较少导致的定位中断问题。

图8 BDS、GPS单系统及BDS/GPS双系统在不同高度角下动态精密单点定位精度Fig.8 Dynamic PPP Positioning Accuracies of BDS, GPS and BDS/GPS at Different Altitude Angles

BDS/GPS双系统精密单点定位精度可满足四川石棉地区地壳形变监测精度要求。当观测环境更差导致BDS/GPS双系统解算无法满足地壳形变监测精度要求时，可考虑同时接收BDS/GPS/GLONASS/Galileo四系统观测值，并通过四系统融合精密单点定位解算提高定位精度以满足地壳形变监测需求。

野外数据采集工作者付出了大量辛苦,武汉大学李星星教授提供了GREAT程序,武汉大学卫星导航定位技术研究中心提供了多系统精密轨道和钟差产品，在此一并表示感谢！