水平大定源回线瞬变电磁任意点一维正反演

石金晶，薛国强,4*，陈卫营，武 欣

(1. 中国科学院地质与地球物理研究所 中国科学院矿产资源研究重点实验室，北京 100029; 2. 中国科学院地球科学研究院，北京 100029; 3. 中国科学院大学 地球与行星科学学院，北京 100049; 4. 西北有色地质矿业集团有限公司，陕西 西安 710054)

0 引 言

回线源瞬变电磁法(TEM)回线装置分为中心回线、重叠回线、分离回线、大定源回线等。中心回线装置由于其理论计算的准确性和对复杂工作环境的适应性被广泛应用于地下水和环境调查，并可作为煤炭和金属矿产的勘探工具。在回线装置中心某一区域接收到的信号没有明显的差异，因此，可以观测大回线中心位置一定范围内的瞬变电磁响应，这被称为改进的中心回线装置。对于改进的中心回线装置，视电阻率的求取通常是利用中心回线装置的公式进行近似计算。然而，这种处理方式往往会导致计算出现系统性的误差而变得不适用。事实上，不仅线框内部有感应场出现，线框外部也有。为进一步提高探测效率，最好的解决方式是实现在一个大的固定回线框内外的任意位置接收信号，即实现大定源回线装置任意点测量。

大定源回线装置一般采用较大边长的矩形回线作为发射装置。相较于中心回线装置和重叠回线装置只在中心点观测的特点，大定源回线装置一旦铺设好回线装置后，可以多台接收机同时工作，不用频繁挪动线框，工作效率较高。而且，大定源回线瞬变电磁探测技术成熟，已经在瞬变电磁正反演研究方面取得了相当大的进展，尤其是一维正反演。在早期关于瞬变电磁的正演研究中多使用圆形发射装置模拟野外多边形(通常是矩形)发射线框。为方便计算，Singh等利用超几何分布函数简化了圆形发射装置的电磁场表达式中的贝塞尔函数，从而得到了任意点圆形发射框的频率域电磁场表达式。Xue等将积分范围分段近似，利用双贝塞尔函数得到了圆形发射回线内外电磁场的表达式。

对于矩形发射线框，圆形线框的公式不再适用，尤其是计算早期响应的时候，因此，必须考虑发射回线形状给出新的计算方法。事实上，无论回线的形状如何，回线内任意一点的电磁场都可以看作回线各边在该点的电磁场之和。为方便计算电磁场，需要对回线源进行剖分，以满足水平电偶极子近似条件，即剖分后的线源到观测点的距离远大于剖分后线源本身的长度，再将水平电偶极子进行数值积分就可得到整个线源的电磁场。Poddar利用电磁互易原理和磁偶极子源得到了频率域电磁场表达式，并对水平电偶极子的频率域响应进行反汉克尔变换，然后将结果进行傅里叶反变换转化为时域。Raiche首先采用嵌套内插值方法得到了一个频域多边形回线发射装置的电磁场表达式，然后通过Gaver-Stehfest变换推导出相应的时域电磁场表达式。Goldman等得到了水平电偶极子源双层介质表面的电磁场表达式，但利用水平电偶极子近似矩形回线时的场表达式比较复杂。此外，国内学者也在电偶极子近似方面做了不少工作。例如，华军等将贝塞尔函数的积分区间分成两段，分别用不同的数值方法进行求解，明显提高了对贝塞尔函数积分的计算效率；李建慧等沿用偶极子合成回线源的思想，获得了大回线源的瞬变电磁响应；李展辉等利用水平电偶极子合成原理，发展了一种适应于任意形状水平接地导线源瞬变电磁法的一维正演方法。赵越等利用贝塞尔函数展开法计算了大回线源非中心点垂直分量与水平分量的电磁响应，对于框外存在过渡区“双解”及“无解”的问题，提出了相应的解决方案。

大定源回线装置虽然提出已久，但是目前国内实际生产中主要还是利用中心回线装置，或者改进的中心回线装置，观测区域局限于发射线框内中间区域的一定范围内，少有对大定源回线框外响应特性及其反演效果的研究。基于此，本文利用毕奥-萨法尔(Biot-Savart)定理计算了大定源回线的一次场，利用偶极子叠加原理计算了均匀半空间大定源回线框内外的二次场响应，通过二次场响应发现晚期段二次场的分布趋于均匀，从而得出在实际观测中可以选择在框内外一定范围观测二次场；在考虑发射框的形状和观测的实际位置情况下，使用该方法对一个三层地质模型进行正反演，获得较好的效果；最后，将该方法应用到湖北省荆州市某机场的大定源回线勘探数据中，取得了较好的效果，反演结果与已有资料具有较好的一致性。

1 理论背景

1.1 一维正演

对于具有一定尺寸的矩形回线发射源，可以采用偶极子叠加的方式来计算其产生的电磁场。叠加方式一般有两种：一种是采用磁偶极子源进行面积分；另一种是采用电偶极子进行线积分。由于采用电偶极子源沿发射线框进行线积分更易于模拟矩形线框，故本文采用这种叠加方式。

图1给出了大定源回线装置电磁响应计算的示意图。回线框的中心在(0，0)处，在方向和方向上的边长分别为2和2，接收装置可以位于回线框的内部或者外部的任意位置。回线框的4个顶点分别用、、和来表示。

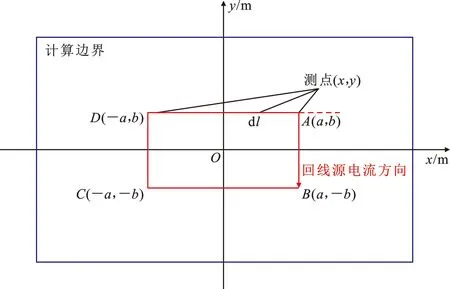
图1 大定源回线装置电磁响应计算示意图Fig.1 Schematic Diagram of Electromagnetic Response Calculation of Large-loop Fixed Source Device

纳比吉安给出了水平电偶极子在均匀层状介质的大地表面上的频率域垂直磁场分量(())表达式。其表达式为

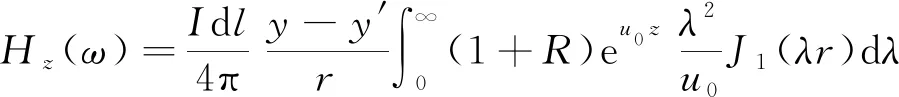
(1)

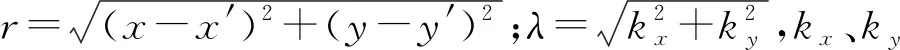
将式(1)进行积分，可以求得长度为2的线源垂直磁场分量为

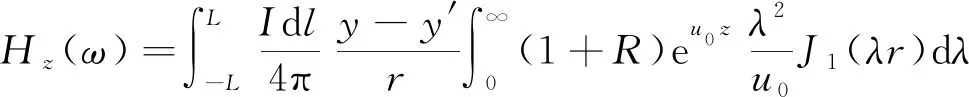
(2)

式(2)为关于贝塞尔函数的无穷积分，无解析解，必须使用数值方法求解。选用滤波系数法求其数值解，将积分形式转化为累加形式。其表达式

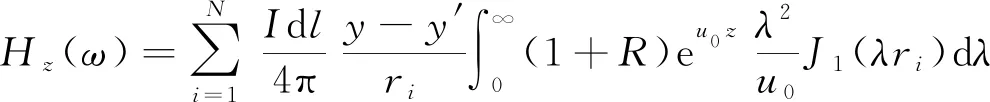
(3)

式中：为线源剖分的偶极子总数；为第个偶极子的收发距；偶极子剖分长度按照d=′50的规则进行确定，其中′为观测点到发射源某个边长的垂直距离。

由式(3)可获得回线框各边的垂直磁场。将各边的垂直磁场相加即可获得整个回线框产生的总垂直磁场为

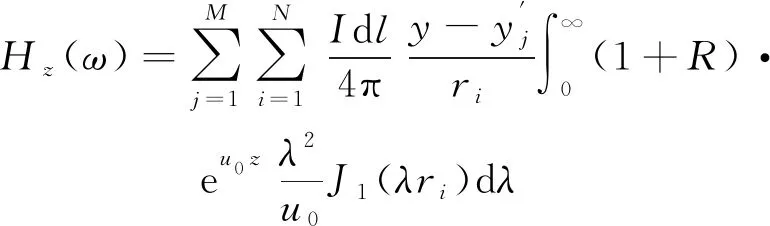
(4)

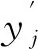
图1所示回线框的总垂直磁场可表示为

(5)

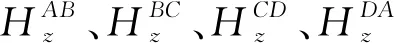
求得频率域场值后，可通过余弦变换将其转换到时间域，得到时刻的阶跃电磁响应。其表达式为

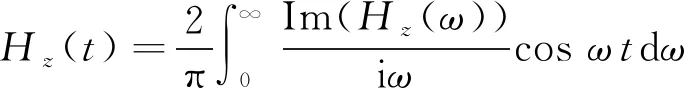
(6)

式中：()为时间域垂直磁场响应。

针对式(4)中涉及的贝塞尔函数积分，本文采用Key等给出的201点滤波系数进行计算。针对式(6)中涉及的余弦变换，本文采用Anderson等给出的787点滤波系数进行计算。

1.2 一维反演

OCCAM反演结果受初始模型影响小，运算稳定收敛。本文采用一阶粗糙度定义模型光滑程度的粗糙度。模型向量数为时的一阶粗糙度()为

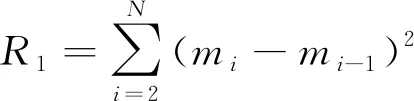
(7)

式中：=(,,…,),代表模型参数向量；是向量的第个分量。

引入粗糙度矩阵，定义为

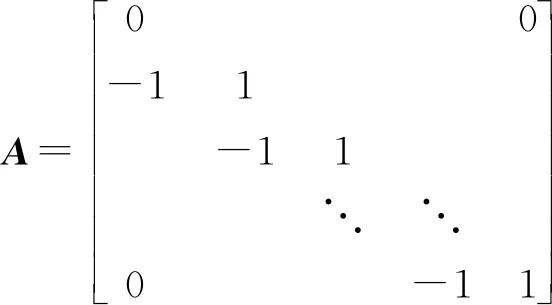
(8)

模型粗糙度可表示为

=‖‖

(9)

定义模型数据与实测数据的拟合残差()，使其遵从加权最小二乘法的原理。其表达式为

=‖-F[]‖

(10)

式中：=diag{1,1,,1}，是误差加权矩阵，1为第个数据点的方差；=(,,…,)代表实测数据向量；[]是模型参数向量对应的正演数据。

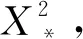
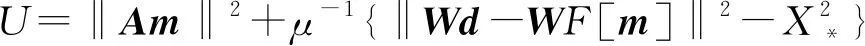
(11)

在反演迭代时，采用局部线性化思想把非线性问题转化为线性问题，对模型参数进行泰勒展开，得到局部近似式子。其表达式为

[+Δ]≈[]+()Δ

(12)

(13)

式中：Δ为向量的修正量；()是×阶雅克比矩阵，和分别为模型向量和数据向量的个数；[]为正演数据向量的第个分量，=1,2，…，。

利用差分思想对式(13)进行计算，将最小化目标函数转化为

(14)

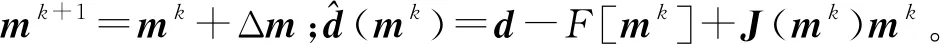
当系数矩阵满秩时，可求得方程组的解为

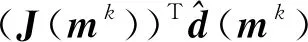
(15)

2 响应特性

2.1 初始场分布特征

瞬变电磁二次场以及一次场的分布与初始场的分布密切相关。在研究二次场特性之前，首先计算矩形回线源在框内外产生的初始场分布特征。初始场(磁感应强度)与模型的电阻率无关，其场值可根据毕奥-萨法尔定理计算，设回线框中电流为1 A，计算网格为5×5 m，结果如图2所示。图2中，“+”表示区域值为正，“-”表示区域值为负。从图2可以看出，框内外初始场的方向相反，初始场幅值最高的区域集中在发射线框两侧很近的距离范围内，框内中心区域的场值分布较为均匀，框外区域随着距离的增大场值迅速衰减，框外150 m处初始场的幅值相比框内中心点的幅值已下降近2个数量级。

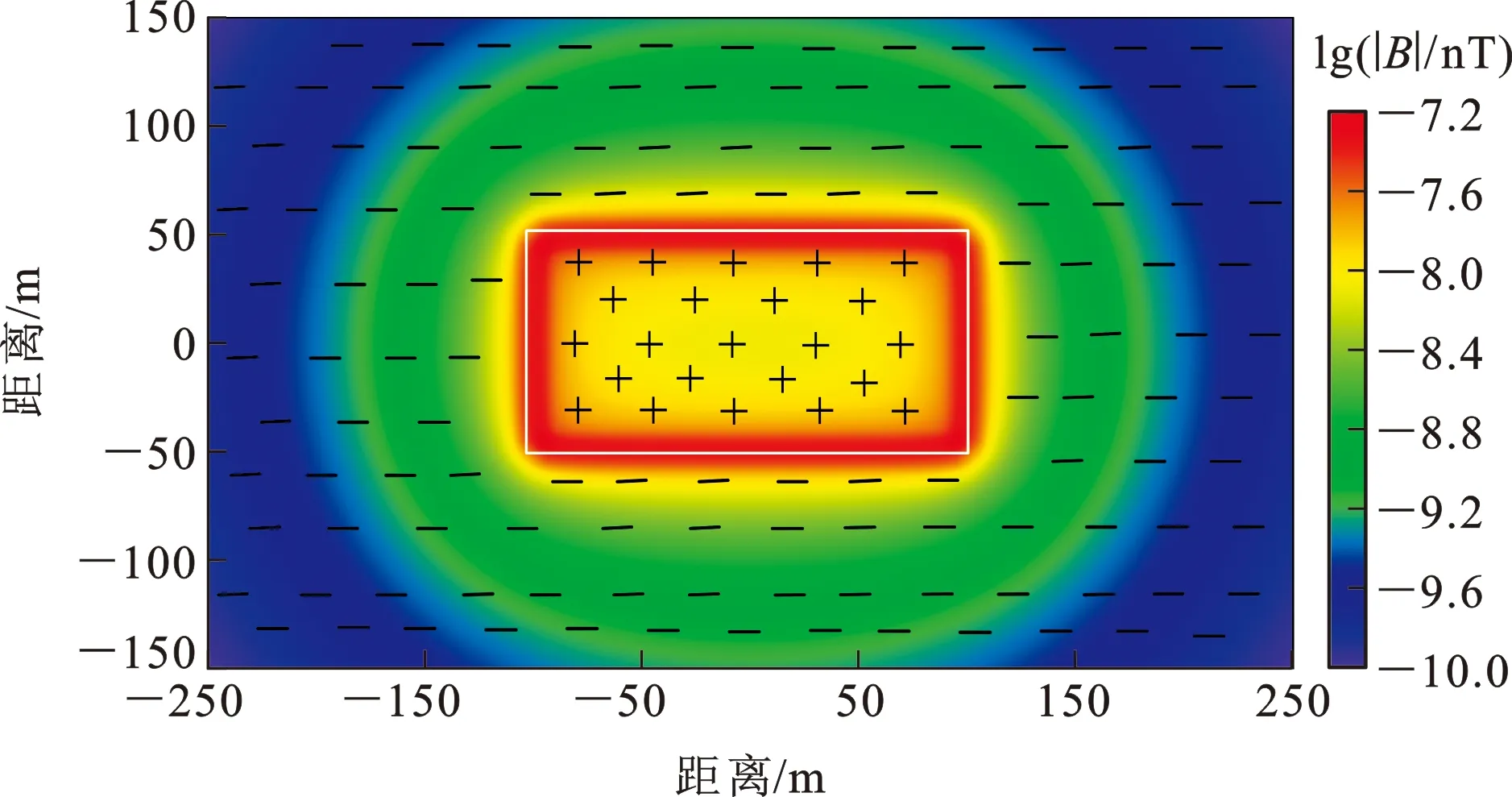
图2 一次场平面分布Fig.2 Plane Distribution of Primary Field

2.2 二次场响应特征

以电阻率为100 Ω·m的均匀半空间模型为例分析二次场的分布与扩散特性，发射源尺寸和计算区域与图3一致。发射电流为1 A，计算时窗为0.01～100.00 ms，共51个时间道，计算场量为垂直感应电动势d/d。其中，为垂直磁感应强度。

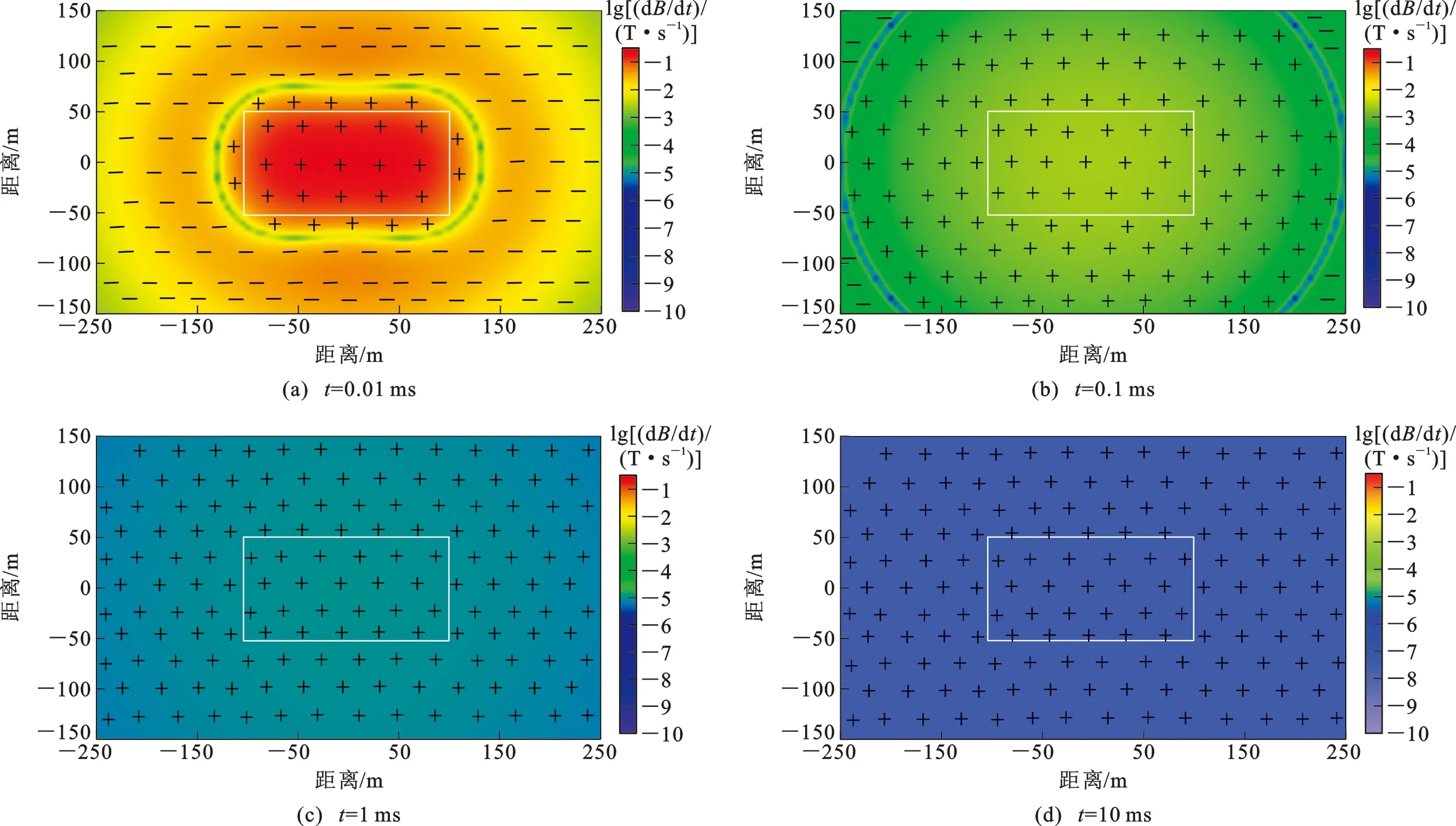
图3 不同时刻二次场平面分布Fig.3 Plane Distributions of Secondary Field at Different Times

首先分析二次场的分布特性，选择所有计算点在0.01、0.1、1和10 ms等4个时刻的响应值，绘制成平面等值图(图3)。图3中，“+”表示区域值为正，“-”表示区域值为负。早期时刻(=0.01 ms)，二次场高值区域主要集中在框内，框外距线框较近处出现符号反转现象；随着时间推移，高值区域逐渐变大，信号反转位置也向外移动[图3(b)、(c)]；当观测时刻为10 ms时，计算区域内的二次场分布趋于均匀，不同位置处的响应差别非常小(均方差仅为0.007)。

图4给出了框内外6个测点的衰减曲线，可以更好地观察二次场随时间的变化特征。当测点在框内时，二次场不发生符号反转现象，但测点位置不同会导致信号在早期幅值不同，靠近中心点处的幅值更高。当测点在框外但距离线框很近时(如=105点)，在计算时窗范围内信号也未发生符号反转，其衰减趋势与框内基本一致；但当测点离发射线框较远时(如=150点和=200点)，早期二次场响应为负，并在某个时刻信号符号转变为正。距离线框位置越远，负值响应的时间范围越长，信号符号反转的时刻也越久。这种框外测点响应符号反转的现象可用烟圈的扩散来解释。无论在框内还是框外，随着观测时间推移，各测点的衰减曲线趋于重合，表明晚期二次场在空间上的分布趋于均匀，发射源和接收点的几何关系带来的影响已非常小。

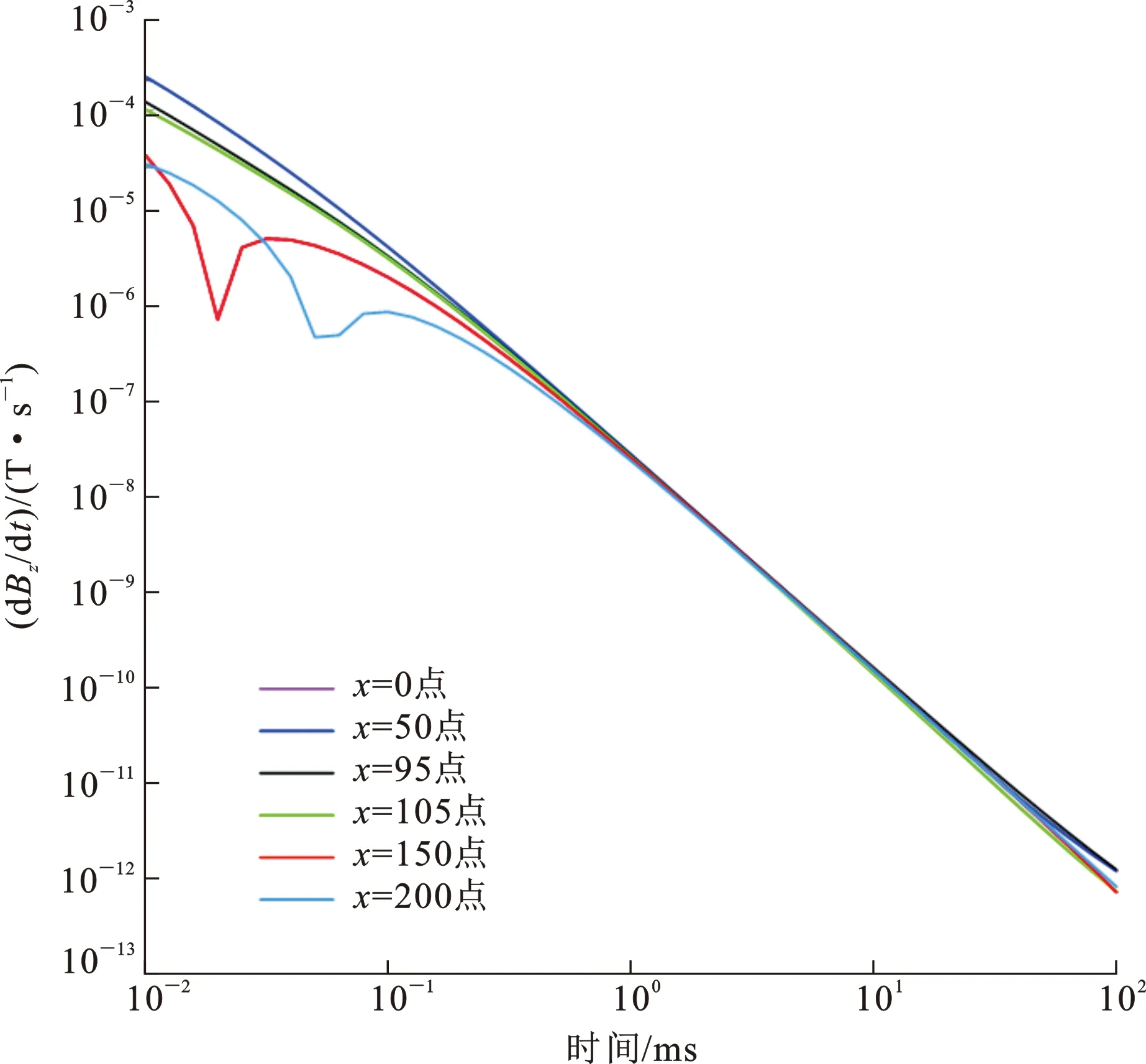
x=0,50,95点为框内点；x=105,150,200点为框外点图4 框内外不同测点的二次场衰减曲线Fig.4 Secondary Field Attenuation Curves of Different Measuring Points Inside and Outside the Frame

上述分析表明，观测点的空间位置不同会导致响应的幅值和形态发生变化，尤其是框外的测点在早期会发生信号符号反转现象，但随着时间推移，观测点空间位置带来的影响逐渐减弱，晚期二次场的分布趋于均匀。因此，在实际观测中，可以选择在框外一定范围观测二次场。

3 一维反演

针对大定源回线装置的数据处理，不能套用中心回线装置的处理方式，必须考虑发射源的实际形状和观测的具体位置。在考虑这两个因素前提下，基于一维正演方法，利用OCCAM算法对数据进行一维反演，并评估反演效果。OCCAM反演是一种带约束性条件的反演方法，它在追求模拟数据与实测数据最大拟合的同时，要求模型数据最平滑，跳出了传统梯度方法简单求取模型增量的模式，而是在对拉格朗日乘子值的搜索过程中寻找靠近极值点的目标模型，保证了算法始终具有很好的稳定性。反演过程中，本文用一维线性搜索法求取拉格朗日算子。

建立一个三层地电模型，各层厚度分别为300和100 m以及无穷大，各层电阻率分别为100、30和80 Ω·m。发射源尺寸为200 m×100 m，测线长度为500 m，点距为5 m，发射源和接收点的几何关系如图5所示。计算电磁场分量为垂直感应电动势d/d，计算时窗范围为0.01～100 ms，共51个时间道。

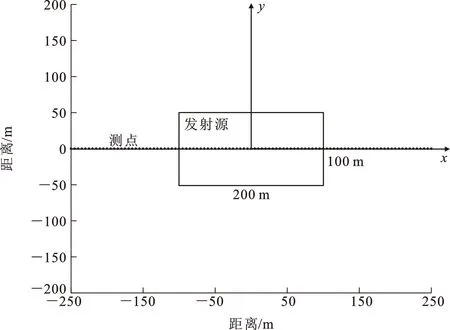
图5 发射源-接收点装置示意图Fig.5 Schematic Diagram of Transmitting-receiving Device

一维正演完成后，对整条线的正演数据进行OCCAM一维反演。设置反演模型最大深度为800 m，共分50层，层厚由浅至深按指数等间隔增加，迭代次数设为10次。结果表明：反演过程中，经过5次迭代后各点的拟合残差都已经下降到2%以内。图6给出了框内外6个测点的数据拟合情况。从图6可以看出，经过10次迭代，无论是框内还是框外的测点都拟合得非常好。图7给出了上述6个测点的反演结果，其表现出了很好的一致性，说明考虑了发射源和接收点实际几何位置的反演，可以很好地恢复地层的真实电性结构。

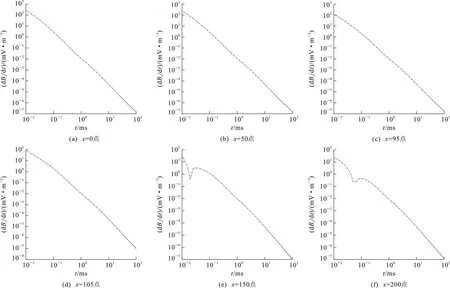
x=0,50,95点为框内点；x=105,150,200点为框外点图6 不同测点的数据拟合情况Fig.6 Data Fitting Curves of Different Measuring Points

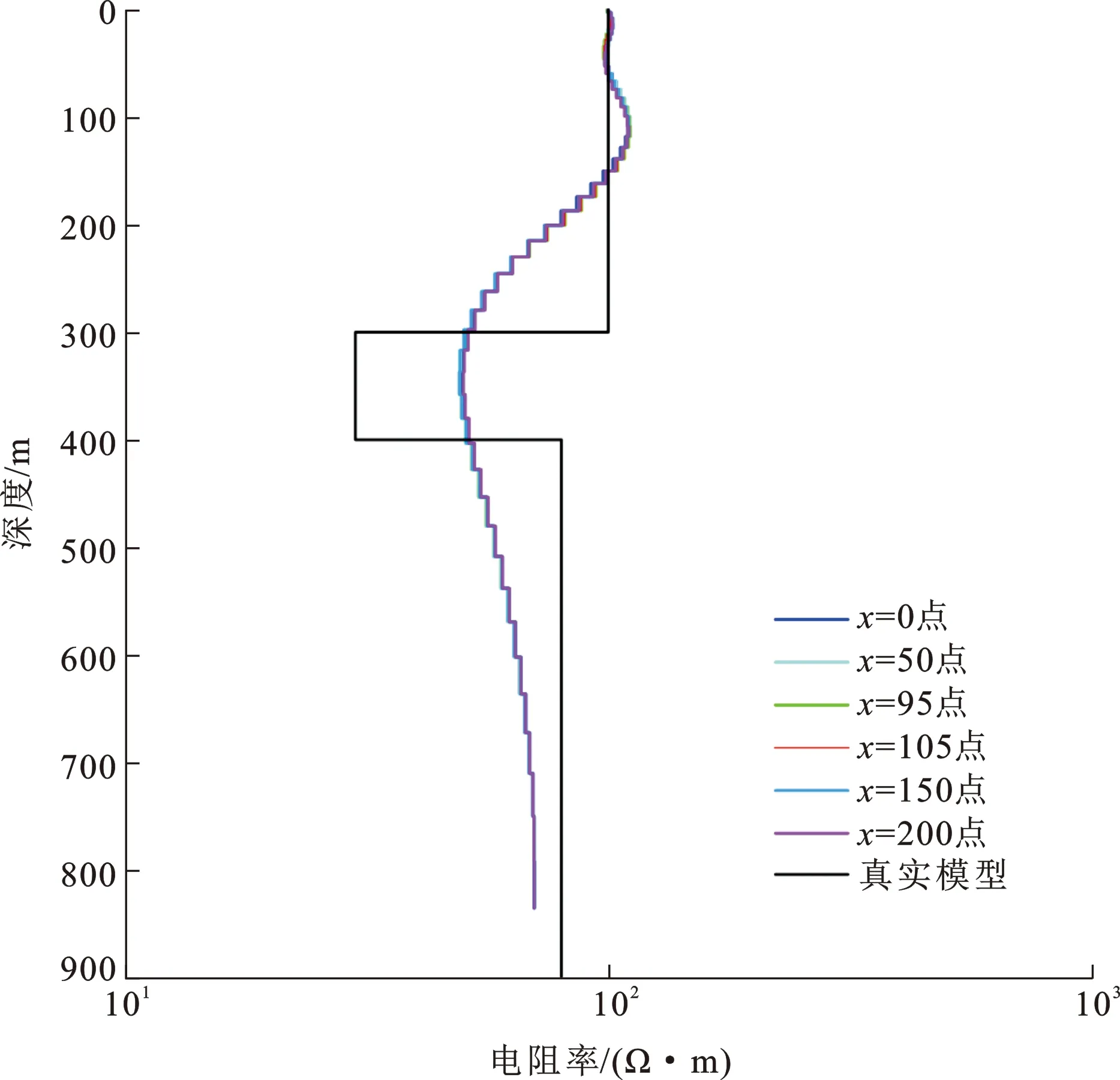
图7 框内外典型测点一维OCCAM反演结果Fig.7 One-dimensional Occam Inversion Results of Typical Measuring Points Inside and Outside the Frame

4 应用实例

在湖北省荆州市某机场进行了大定源回线装置的探测试验，并利用本文提出的正反演方法对实测数据进行了处理。根据已有地质地球物理资料，试验区上覆较厚的第四系和第三系沉积层(厚度大于500 m)，岩性主要为黏土、泥质粉砂、粉砂、砾石层等，地层电阻率整体偏低。本次测量的目的是探测区内浅表含水层及下部隔水层的深度，并评估其横向连续性。试验工作中，测线总长度为1 200 m，点距为20 m，共布置4个矩形发射线框，尺寸为200 m×100 m，每个发射线框控制测线长度为300 m，发射源-接收点布置如图8所示。受工作区茂密的植被影响，发射线框未能布置成标准的矩形，根据GPS记录的航迹绘制了实际的布置形状。工作仪器为TerraTEM，发射电流为5～9 A，基频为5 Hz，观测垂直感应电压分量，接收探头有效面积为10 000 m，叠加次数为256次。

图8 发射源-接收点布置图Fig.8 Transmitter-receiver Layout

区内整体干扰水平较低，实测衰减曲线在大部分计算时窗范围内都较为光滑，仅在晚期出现一定程度的震荡。图9给出了框4控制的16个测点的实测归一化(电流和接收有效面积归一)信号曲线，其中仪器记录的关断时间约为220 μs。在关断期间，同时存在一次场和二次场，但一次场的强度要远高于二次场，因此，在220 μs之前的时刻，响应曲线主要表现的是一次场的特性。从图9可以看出：当测点位于框内时(960～1140点)，未关断的一次场为正值；而当测点位于框外时(900～940点、1160～1200点)，未关断的一次场为负值；这与图2、3给出的结论相吻合。图10给出了所有测点的多测道曲线。为避免信号符号反转给数据分析和处理带来的不便，将起始时间道(288.5 μs)选在框外测点出现负响应的时刻之后。从图10可以看出：不考虑晚期受干扰信号情况下，4个发射框控制的测点响应整体上较为均匀；但当测点在框外时，响应值会出现明显的降低，如图中黑色虚线框圈出的位置。

对所有测点的数据进行掐头去尾处理并进行五点圆滑滤波处理，得到光滑衰减的信号曲线，然后利用OCCAM算法对整条测线的数据进行一维反演。反演最大深度取600 m，共分40层，迭代次数为10次。正演部分中，发射源按照实际布设形状进行路径积分。图11给出了所有测点的最终拟合残差。从图11可以看出：数据拟合程度较好，除个别测点因干扰程度较大导致拟合残差较大外，其他测点的拟合残差都在5%以内。

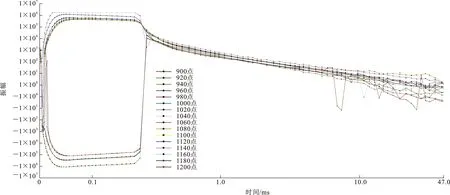
图9 框4控制测点的实测归一化响应曲线Fig.9 Measured Normalized Response Curves of Control Measuring Points in Loop 4

图10 所有测点的多测道响应曲线Fig.10 Multi-channel Response Curves of All Measuring Points

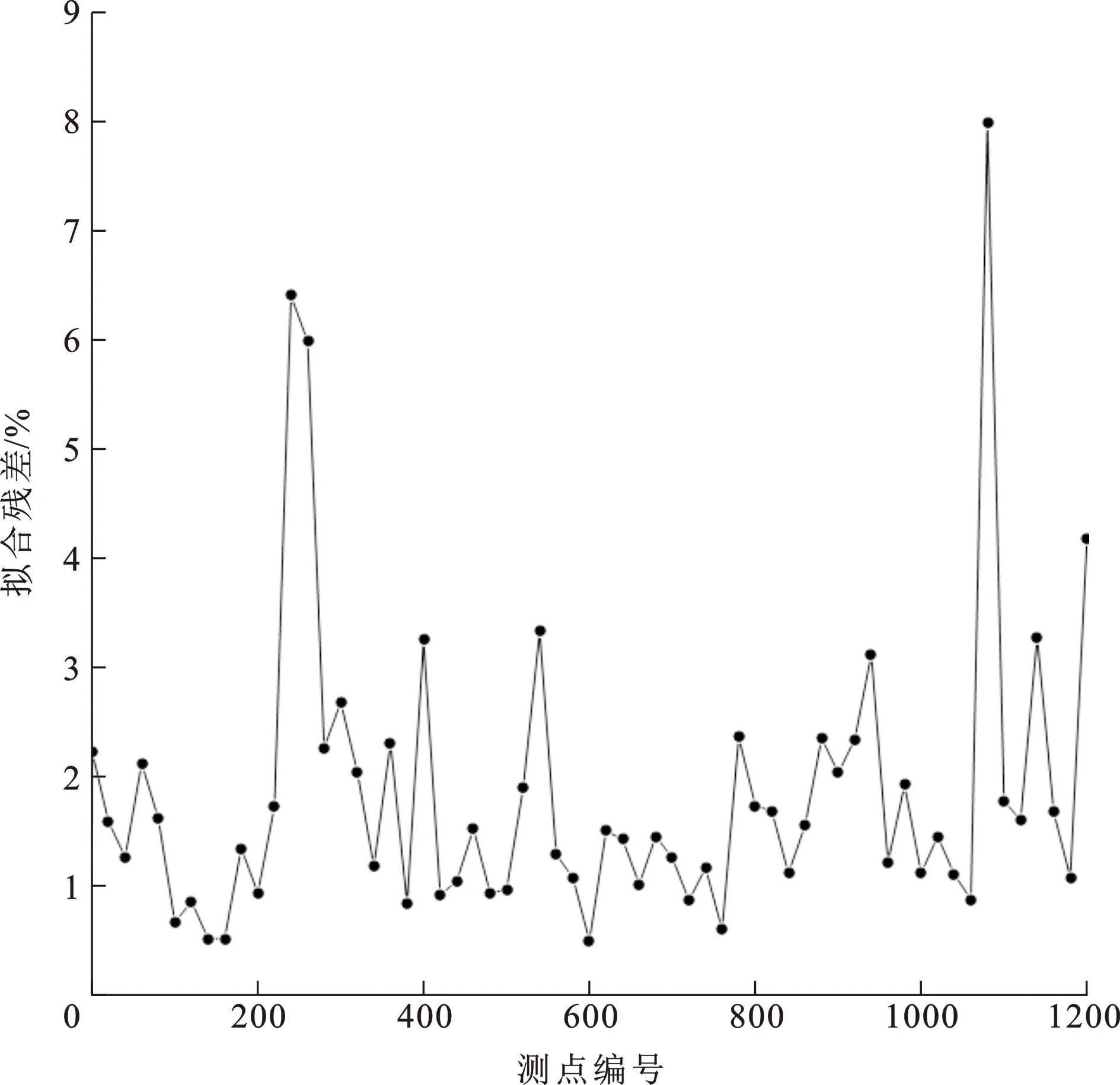
图11 所有测点迭代10次的拟合残差Fig.11 Fitting Residuals of All Measuring Points with 10 Iterations

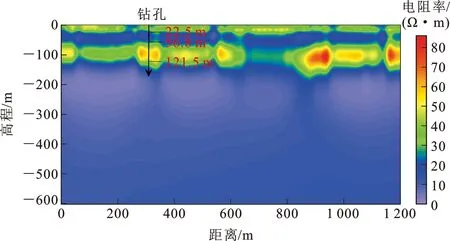
图12 电阻率-深度反演断面Fig.12 Inversion Section of the Resistivity-depth

图12给出了整条测线的反演电阻率-深度断面图。从图12可以看出，测区整体电阻率较低，符合该区厚新生代沉积层的实际地质情况。根据反演结果，可以确定区内含水层深度范围为20～60 m，下伏表现为相对高阻的隔水层(厚度约为60 m)。含水层在横向上厚度较为均匀，表现出较好的连续贯通性。隔水层电阻率在横向上出现一定程度的突变，推测可能与地层的完整性、空隙度、含水性等因素有关。在测点300处有一个钻进深度约150 m的钻孔，钻孔揭示含水层的顶界面深度为22.5 m，隔水层顶界面深度为56.8 m，隔水层底界面深度为121.5 m，该结果与反演结果基本一致，验证了方法的有效性和准确性。

5 结 语

本文针对回线瞬变电磁法中的大定源回线装置开展了理论分析和应用研究。通过对矩形回线框内外一次场、二次场的计算以及对三层地电模型和野外实测数据进行反演，得到以下结论。

(1)利用电偶极子沿发射线框进行线性积分，可以准确获得大定源回线装置发射线框内外任意点的瞬变电磁场。

(2)不同观测点空间位置会导致响应的幅值和形态发生变化，尤其是框外的测点在早期会发生信号符号反转现象，但随着时间推移，观测点空间位置带来的影响逐渐减弱，晚期二次场的分布趋于均匀。因此，在实际观测中，可以选择在框外一定范围观测二次场。

(3)在进行一维反演时，考虑发射线框的形状和实际的观测位置等因素，可以很好地反映地层的电性结构，使反演结果更加可靠。