多类时延下混合车辆队列建模与协同控制*
胡满江,卜令坤,秦洪懋,周岩,边有钢,孙宁,郑讯佳
(1.湖南大学机械与运载工程学院,长沙410082;2.湖南大学无锡智能控制研究院,无锡214072;3.潍柴智能科技有限公司,潍坊261000;4.重庆文理学院智能制造工程学院,重庆402160)
前言
近年来,智能网联汽车(intelligent and connected vehicle,ICV)的飞速发展成为新一轮科技革命和中国汽车工业转型升级的重要支柱。ICV作为集环境感知、规划决策、控制执行和信息交互等于一体的高新技术综合体,具有极大的产业价值和社会价值;因此,近年来得到国内外学者的广泛关注和研究。作为智能网联汽车的典型应用之一,车辆队列协同控制技术被认为具有改善燃油经济性、提高驾驶安全性和提升交通流量的巨大潜力。
现有研究大多集中在完全网联交通环境,即车辆队列全部由网联自动驾驶车辆(connected automated vehicle,CAV)组成。郑洋提出了一种车辆队列建模的四元素架构,包括车辆动力学模型、通信拓扑、车辆间距策略和分布式控制器,为队列的分析和控制提供了一种可行的统一化视角。在系统控制性能方面,主要考虑的是内稳定性(internal stability)和队列稳定性(string stability)。内稳定性即闭环稳定性,它要求所有车辆跟驰误差渐近收敛至零。对于线性系统而言,内稳定性即要求系统特征值均具有负实部。针对线性车辆动力学模型,Zheng等研究了通信拓扑矩阵特征值均为实数的系统内稳定性,基于特征值分解的方法将系统解耦进而利用Routh-Hurwitz判据推导内稳定性的充分必要条件;Li等考虑了通信拓扑矩阵存在复特征值的情况,并基于模态标准型进行系统结构分解推导了闭环稳定性的充要条件以及设计了具有指数级收敛的分布式控制器。
上述研究都是针对同类车辆模型,Bian等考虑了异类的3阶车辆模型,推导了保障系统稳定性的充要条件,得出了异类车辆车头时距与惯性时滞和控制增益的关系;秦晓辉等提出了对称通信拓扑下具有不同参数摄动的非同类车辆队列鲁棒稳定性分析方法和分布式控制器设计方法;Guo等采用径向基函数神经网络和PID型滑模控制方法,提出了一种自适应容错排控制方案,实现了单车稳定性、队列稳定性和交通流稳定性;Guo等针对在执行器饱和、参数不确定和未知干扰的情况下,提出了自适应滑模控制方案,实现了参数异质车辆队列控制的跟踪问题;Xu等基于Lyapunov-Krasovskii设计了控制器,实现了在参数不确定性和通信时延等外部干扰情况下的闭环稳定性;Xiao等基于恒定车头时距间隔策略设计了滑模控制器,保证了异类车辆队列的稳定性。杨泽宇等提出一种严格避撞的分布式鲁棒控制器设计方法,结合车间距势函数、自车与邻近车辆状态和动力学不确定边界设计了分布式鲁棒控制律。鲁若宇等基于队列系统的多项优化性能设计代价函数和系统约束提出一种分布式模型预测控制(DMPC)策略,通过系统局部代价函数之和构建Lyapunov候选函数,证明了车辆队列系统渐进稳定性的充分条件。Ghasemi等基于偏微分方程理论,分析了双向拓扑下系统内稳定性的条件;Hu等考虑通用信息拓扑,基于黎卡提方程,设计了参数异质车辆队列的分布式自适应控制器;马芳武等从车辆间距策略出发,基于非线性车距控制的驾驶行为决策模型,保证了队列系统的稳定性。另外,模型预测控制(MPC)方法在车辆队列控制中也得到广泛应用,例如Li等提出了一种分布式MPC方法用于切换通信拓扑下车辆队列的协同控制;Bian等针对燃油经济性的问题设计了分布式经济模型预测方法能同时降低通信负担和优化燃油经济性。
然而,当前由以人工驾驶车辆(human-driven vehicle,HDV)为主导的交通环境向完全自动驾驶交通环境的发展进程中,必然存在着既有人工驾驶车辆又有网联自动驾驶车辆的混合交通环境。胡笳等考虑道路交通特性、道路结构和匝道汇入前主线交通状态等因素的交互作用机理,建立快速路合流区通行能力模型,定量描述不同道路条件下合流区通行能力如何随网联自动驾驶渗透率和队列长度而变化。李永福等考虑V2V通信时延,设计一种分布式非线性轨迹跟踪控制器,使用Lyapunov方法证明了所设计控制器的稳定性;进一步李永福等针对通信延时环境下的异类车辆队列控制问题,提出了一种基于3阶模型的分布式非线性车辆队列纵向控制器,利用Lyapunov-Krasovskii定理对车辆队列的稳定性进行分析,得出车辆队列的稳定性条件和通信延时上界。Zheng等研究了封闭环形道路上CAV对交流量、交通扰动的影响机理;从理论层面揭示了混合车辆队列系统能控性和能观性,并从系统级层面设计了控制器以衰减交通流的波动。杨依琳等研究了基于最优控制模型(OVM)的混合车辆队列协同控制方法;在控制器中引入了后车信息,基于首尾误差传递函数给出了系统闭环稳定性和首尾稳定性的定性判据,进而通过数值仿真分析了CAV对队列稳定性、跟踪性能和燃油经济性的影响。另外,在网联自动驾驶车辆通过无线通信(vehicle-to-vehilce,V2V)接收邻近车辆的信息时,不可避免地存在通信时延。目前关于时延的研究多集中在完全网联车辆队列的通信时延,例如:Di Bernardo等针对车辆队列存在异质通信时延问题,应用Lyapunov-Razumikhin理论设计了分布式一致性控制器;Wu等基于方法为考虑随机通信时延的车辆队列设计了协同控制器,保证了系统的内稳定性;Ge等同时考虑通信时延和驾驶员反应时延为车辆队列设计了分布式最优控制器;Gao等采用鲁棒控制方法分析了通信时延对异类车辆队列的影响;Elahi等考虑了通信时延和随机丢包为多智能体系统设计了一致性控制器。除通信时延外,在混合车辆队列中,还存在通过车载传感器监测前方车辆状态时的传感器量测时延和人类驾驶车辆存在的驾驶员反应时延等。上述多类时延在实际行驶工况中客观存在,但在混合车辆队列中的研究较少,对系统性能的影响尚未得到充分重视。因此,针对上述问题,本文中研究多类时延下混合车辆队列建模与协同控制方法,主要贡献如下。
(1)考虑通信时延和传感器量测时延,并在OVM基础上引入驾驶员反应时延进行HDV非线性驾驶行为描述,构建了包含多类时延的混合车辆队列系统模型。该模型可对混合车辆队列中CAV数量与空间分布进行表征,为通用交通场景下混合车辆队列建模提供统一的框架。与文献[21]中所考虑的封闭环形道路车辆队列相比,本文建立的开放道路下混合队列模型,更具有实际意义;与文献[25]中基于OVM对HDV行为的描述相比,本文进一步引入驾驶员反应时延,更能体现实际混合车辆队列的动态特性。
(2)基于自车和邻近车辆加权误差,设计了混合车辆队列的状态反馈控制器,推导了带多类时延的闭环系统特征方程,并解析导出了系统闭环稳定性的充分条件,保证多类时延下混合车辆队列跟踪误差的渐近稳定。
(3)与文献[25]中对系统稳定性进行数值求解不同,本文中针对上述闭环系统模型解析地求解出系统特征方程,并给出显式的渐近稳定充分条件,可为CAV不同数量和空间分布的混合车辆队列系统提供通用的稳定性设计方法。
1 系统建模
首先建立HDV和CAV纵向跟驰模型。然后,对于单车道上行驶的混合车辆队列(见图1),建立包含1辆CAV和+辆HDV的统一模型描述。其中,CAV编号为0,其前面有辆HDV,编号依次为-1-2…-,记={-1,-2,…,-};其后面 有辆HDV,编 号 依 次 为12…,记F={1,2,…,}。CAV通过V2V通信接收来自前车和后车的状态信息。第辆车的位置、速度分别用p()和v()表示。不失一般性的,车辆长度用表示。相邻两辆车之间的间距误差记为:s()=p()-p()-。由++1辆车组成的混合车辆队列跟驰领航车匀速行驶。领航车位置和速度由()和()表示,仅作为-车的跟驰信息。下面,将对单个HDV、CAV和整个混合车辆队列系统进行建模。
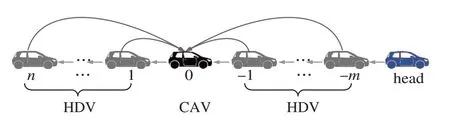
图1 混合车辆队列
1.1 HDV的纵向跟驰模型
HDV的纵向跟驰模型在已有文献中有多种应用形式,应用比较广泛的有最优控制模型(OVM)、智能驾驶员模型(IDM)和基于二者的衍生模型。通常,这些模型都可以采用下面的非线性函数描述:

式中τ为驾驶员反应时延。
从式(1)可以看出,HDV的加速度是前车的间距、相对速度和自车速度的函数;另外,式(1)只考虑了驾驶员反应时延的差异,而未考虑驾驶员行为函数的差异。车辆队列稳定行驶时的期望间距和期望速度记为(s,v),即稳态点。当车辆状态处于稳态点时,有[s,0,v]=0。假设HDV的状态量均在稳态值附近波动,由此定义第辆HDV的误差状态变量为

对式(1)在稳态点(s,v)处进行1阶泰勒展开,可以得到每一辆HDV的线性模型:
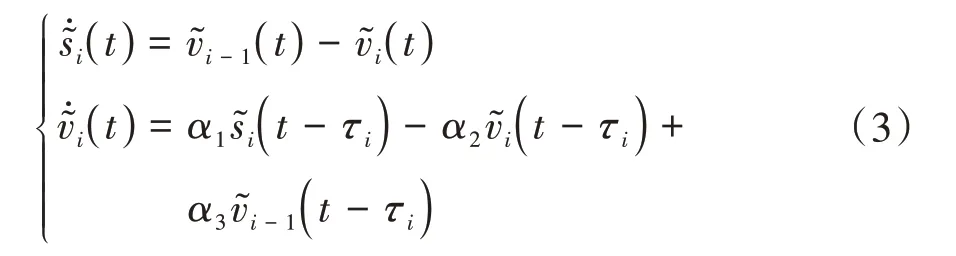


式中:(s())表示期望速度与相邻间距的函数关系;>0反映了驾驶员对自车速度与(s())差值的敏感度;>0反映了加速度对自车和前车相对速度的敏感度。通常,(s())由下面的连续函数描述:

其中当相邻两辆车的间距较小时(≤),期望速度为0,车辆处于静止状态;当相邻两辆车的间距较大时(≥),车辆以最大速度行驶;当相邻两辆车的间距处于和之间时,通常期望速度按照函数f()随的增大而单调增加。f()有线性或非线性的形式;考虑到实际驾驶加速度的连续性,f()一般选择下面的非线性形式(如图2所示,其中=5 m,=35 m,=30 m/s):

图2 OVM模型中函数V(s)的曲线

在稳态点(s,v),有v=(s)。进一步,根据式(3)可得到下面的关系:
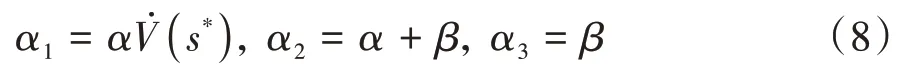

1.2 CAV模型
对于CAV,采用双积分器的线性模型,加速度信号直接作为控制输入,即
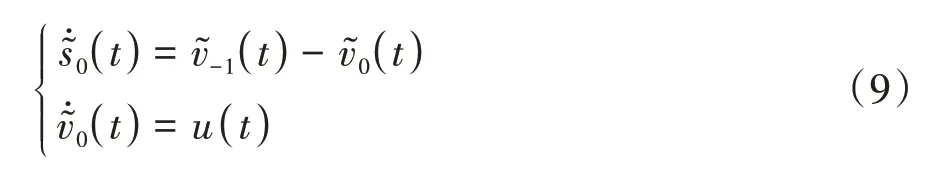
1.3 系统模型

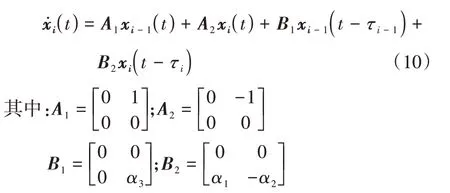
特别的,对于-车,有:

式中()是领航车的状态向量。若假定领航车无扰动,则()=0。式(10)可写成:

式中=[0 1]。
定义集总状态向量:

为方便推导,考虑匀质驾驶员反应时延,即τ=,∈∪F,则系统方程可写为

其中:

当领航车以期望速度行驶时,有=0,此时式(13)可简化为
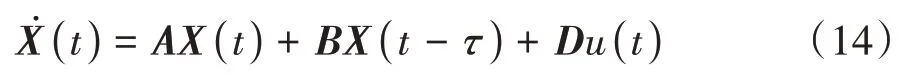
2 控制器设计与系统稳定性分析
2.1 控制器设计
针对式(14),采用自车误差和邻近车辆的误差作为反馈信息,将CAV状态反馈控制器设计为
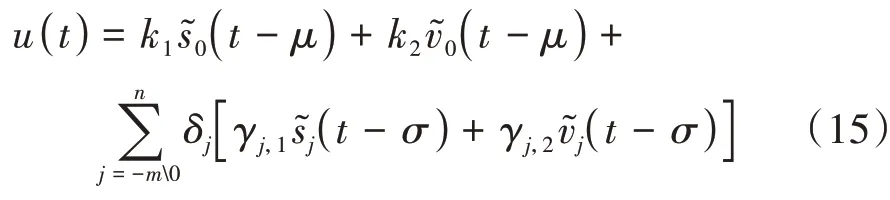
式中:为CAV与邻近车辆的通信时延;δ描述CAV是否能接收到第辆HDV的信息,当可以接收时取δ=1,否则δ=0,(∈∪F);CAV采用车载传感器获取前车(-1车)的间距和速度等信息,而车载传感器量测时延记为。将式(15)简写为


将式(16)代入式(14),得到系统闭环状态方程:

2.2 系统稳定性分析
下面推导式(17)闭环稳定性的充分条件。


定理1:对于混合队列交通系统式(14),采用式(16)的控制输入,当式(19)成立时,式(14)是渐近稳定的:
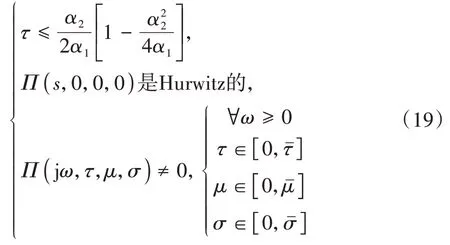

证明:先求出式(17)的特征多项式:

其中(,)和(,,,)形式见式(21)和式(22)。
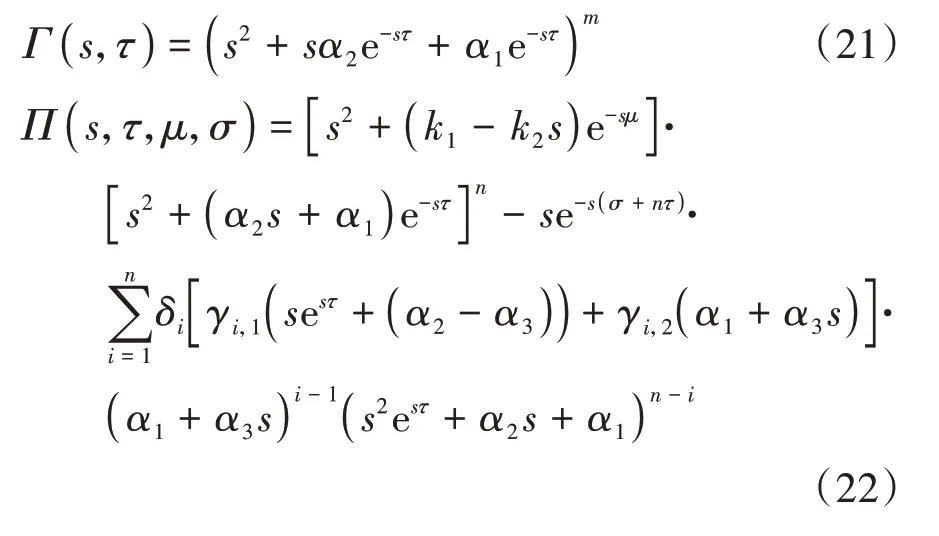

由此得到式(19)。
定理得证。
定理1中式(20)受通信拓扑和前后车数量的影响,难以导出解析条件。在下文中将针对具体的拓扑形式进行仿真以验证定理的正确性。
3 仿真与实车验证
3.1 数值仿真验证
采用OVM作为HDV的描述模型,对两组场景仿真,即=5,=5,CAV分别有1辆和2辆,见图3;然后针对场景1分析时延对系统性能的影响。
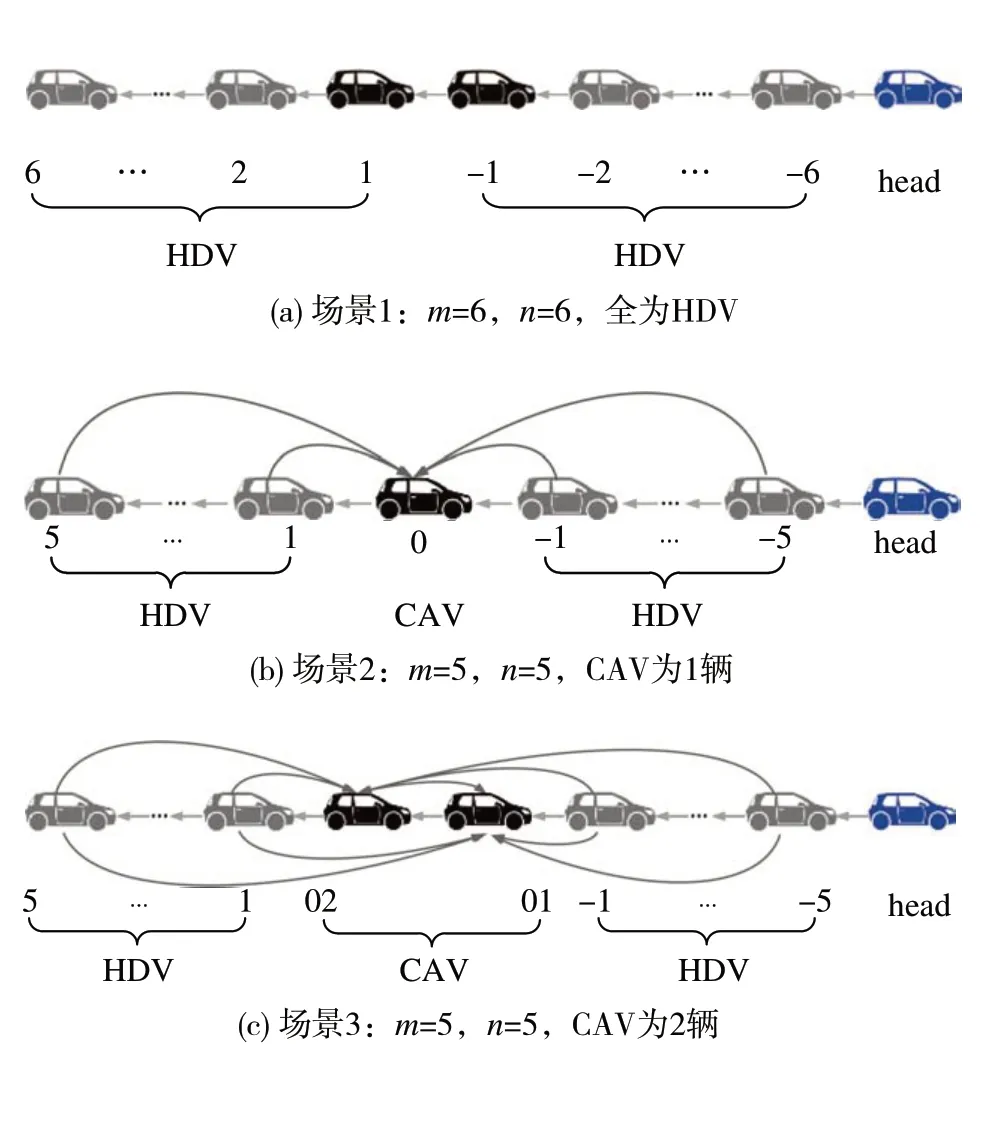
图3 数值仿真试验场景
一般的,选择=30 m/s,=5 m,=35 m,v=15 m/s,s=20 m。由式(7)可知:N=π/2。根据文献[33],选取=0.6,=0.9。由式(8)可得
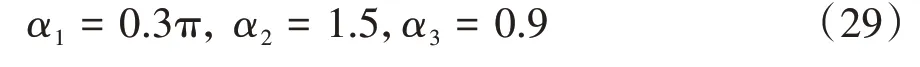
领航车以=15 m/s的速度匀速行驶,加速度轨迹按照式(30)变化,如图4所示。

图4 领航车速度轨迹图

3.1.1 场景1仿真验证
12辆HDV作为跟驰车辆,领航车的位置、速度轨迹可以根据式(30)获得,所有跟驰车辆根据前车跟随式的信息流拓扑结构获取所需的信息,基于OVM计算自车的期望输入。车辆队列行驶间距误差和速度误差如图5所示。
3.1.2 场景2仿真验证
为便于计算,通信拓扑取δ=1(=-5,…,-1,1)。根据式(19),有≤0.321 s,即驾驶员反应时延的上限不应大于0.321 s。对于式(20),有
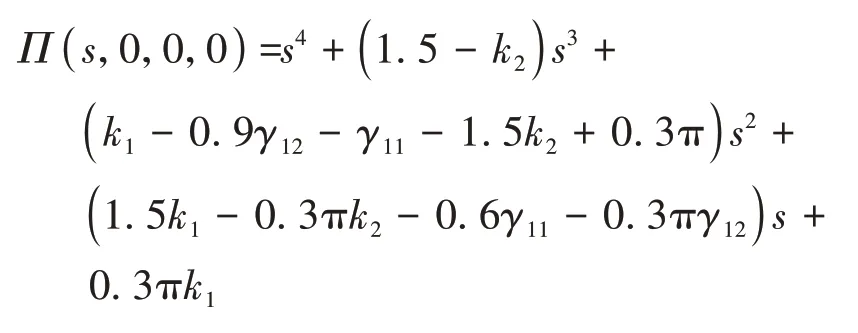
为方便推导,将反馈控制增益设置为匀质的,即γ=γ≔,∈∪F。则

根据Routh-Hurwitz判据,选择=0.7,=0.6,=-1.3,可使式(31)是Hurwitz的。进一步,选定上述控制增益后,将传感器时延和通信时延从0~1 s以0.01 s的间隔遍历,已验证(j,,,)≠0,即系统是稳定的。
由12辆HDV组成的车辆队列行驶间距误差和速度误差作为对照组,如图5所示;场景2的混合车辆队列行驶误差如图6所示。从图5(a)与图6(a)、图5(b)与图6(b)的对比可以看出,当队列中包含有CAV时,其间距误差和速度误差均会被衰减。CAV后面的1~5号跟驰车辆,间距误差和速度误差的峰值衰减幅度高于35%,见图7。因此,验证了本文理论分析的正确性。

图5 场景1不含CAV的12辆HDV队列行驶误差
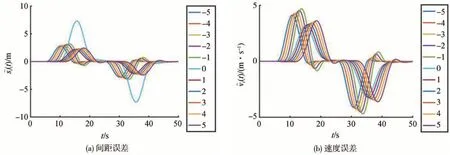
图6 场景2混合车辆队列行驶误差对比
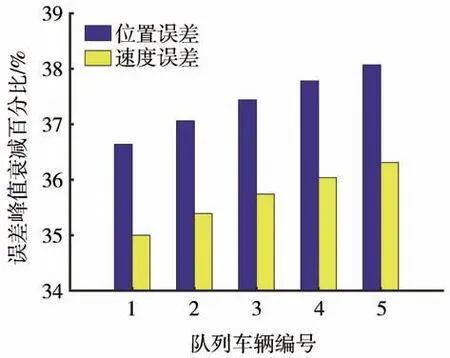
图7 场景2 CAV后的1~5号车位置和速度误差峰值衰减百分比
3.1.3 场景3仿真验证
进一步,场景3设定为包含2辆CAV。其间距误差和速度误差见图8。对比图5(a)与图8(a)、图5(b)与图8(b)可看出,间距误差和速度误差衰减的效果更好。CAV后面的1~5号跟驰车辆,间距误差和速度误差的峰值衰减幅度高于67%,见图9。因此,进一步验证了本文理论分析的正确性。
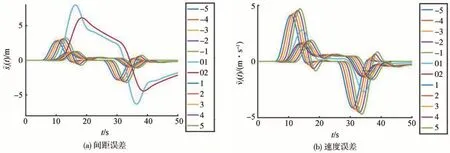
图8 场景3混合车辆队列行驶误差

图9 场景3 CAV后的1~5号车位置和速度误差峰值衰减百分比
3.1.4 时延对系统性能的影响
为研究传感器量测时延和通信时延对速度误差峰值的影响,对场景2中CAV后面的1~5号跟驰车辆的速度误差峰值进行了仿真分析,如图10所示。
从场景2的图10可以看出,速度误差峰值随交通流向后方传播而增大,这是由于人工驾驶车辆无法及时、快速感知前方车辆状态信息而引起的误差放大。就单个跟驰车辆而言,速度误差峰值随通信时延的增大而增大、随着传感器量测时延的增大而减小。通信时延导致了CAV获取邻居车辆信息的滞后性,从而使CAV总是落后期望位置而产生误差,这一误差随下游车辆传播而增大。在CAV收敛至平衡状态时,控制器计算所用的反馈误差与真实的实时误差不同,其会随传感器量测时延增大而增大;这等价于反馈增益增大,给CAV更大的输入控制量,从而导致速度误差峰值随传感器量测时延的增大而减小。
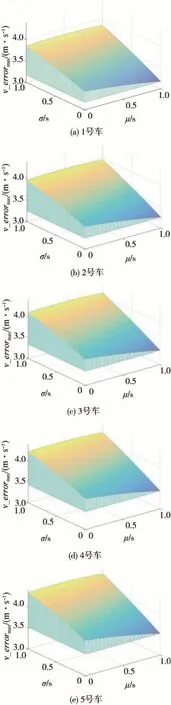
图10 CAV后的1~5号车速度误差峰值随μ和σ的变化
3.2 实车测试验证
本文实车测试验证试验基于3辆AGV(automated guided vehicle),见图11。AGV底盘基于期望速度控制,对于决策层向底盘下发的期望加速度指令,通过数值积分算法可获得期望速度。每辆AGV均配有GNSS设备,可实时获取位置信息;通过底盘CAN总线读取实时速度信息。AGV每10 ms采集一次位置和速度信息并发送至决策层,即传感器量测时延约10 ms。另外,AGV之间通过WiFi进行实时通信,通信时延约10 ms。领航车的加速度曲线由式(32)表示,边界条件设置为(0)=0,(0)=0。基于此,先后进行两次对比试验。

图11 AGV试验平台

3.2.1 基于OVM的混合车辆队列对比试验
该项对比试验将进行试验组和对照组两次试验。试验方案设计如图12所示。首先,将3辆AGV分别编号为1、2、3,作为跟驰车辆。根据式(32)可获得领航车的位置和速度轨迹,将其存于1号AGV本地储存器。在对照组中,跟驰车辆1、2、3的决策层基于OVM计算得到自车的期望输入。其中,1号AGV通过本地读取领航车的位置和速度轨迹信息作为OVM的输入;2、3号AGV通过WiFi通信获取前车的位置和速度信息作为OVM的输入,以模拟真实驾驶员通过观测路况获取环境信息;在试验组中,仅2号AGV有所不同,即通过WiFi通信获取1、3号AGV的位置和速度信息并根据本文所提算法,即式(15),计算得到期望输入,其他均与对照组相同。两组试验分别记录3辆AGV的速度信息。另外,本项试 验 中OVM参 数 选 择 为v=1 m/s,=1.5 m/s,s=1.33 m,=2.33 m,=0.33 m,=1 m,=0.6,=0.9。试验结果如图13所示。

图12 基于OVM的混合车辆队列对比试验方案设计
图13(a)示出3辆AGV均为OVM,即模拟驾驶员行驶的速度轨迹图,3辆AGV均能有效跟踪前车,但随着队列车辆编号的增大峰值渐长,且随着稳态速度的增大,队列性能急剧恶化;图13(b)示出1、3号AGV为OVM、2号AGV为CAV的情形。可以看出,2号车有效延缓且衰减了1号车的速度波动,从而验证了本文所提理论的正确性。
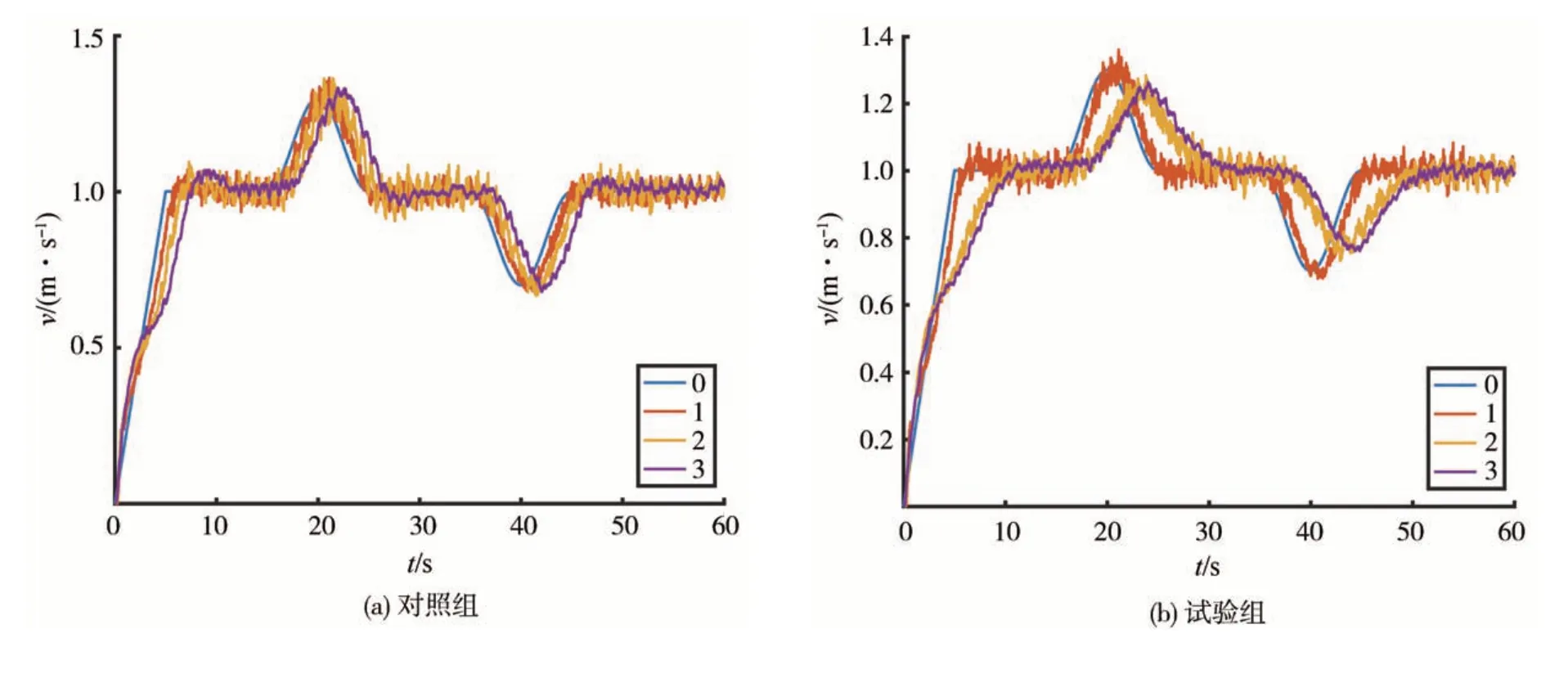
图13 基于OVM的混合车辆队列对比试验
3.2.2 基于人工控制的混合车辆队列对比试验
该项对比试验也分为对照组和试验组,试验方案设计如图14所示。在对照组中,3名驾驶员分别控制1、2、3号AGV的速度,其中1号驾驶员依据随机驾驶意图控制1号AGV行驶,2、3号驾驶员控制2、3号AGV与1号AGV保持期望间距。在试验组中,1、3号AGV依然由驾驶员控制,执行与对照组中相同的功能要求;2号AGV设置为CAV模式,通过WiFi通信获取1、3号AGV的位置和速度信息,并根据本文所提算法式(15),计算期望输入并发送至底层进行控制。两种试验分别记录3辆AGV的速度、速度误差和位置误差等信息,以此验证本文所提算法在人工控制AGV中衰减误差波动的作用。
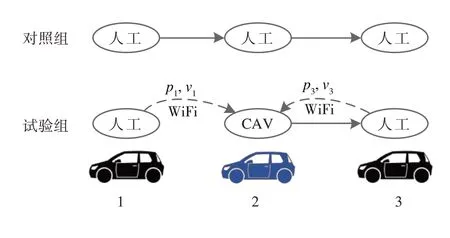
图14 基于人工控制的混合车辆队列对比试验方案设计
本项试验结果如图15所示。在对照组(图15(a)~图15(c))中,1号车发生速度缓变或突变时,2、3号车的速度受其影响波动较大,且速度波动随车辆编号增大呈现放大趋势;速度误差和位置误差也随着向后传播不断恶化。对比试验组(图15(d)~图15(f)),显然作为CAV的2号车能够“吸收”1号车的速度波动,有效衰减干扰误差峰值改善交通流。上述结果验证了所提出控制方法的有效性。

图15 基于真实人类驾驶的混合车辆队列对比试验
4 结论
考虑V2V通信时延、传感器量测时延、驾驶员反应时延等多类时延的影响,建立了一般形式的混合车辆队列模型,设计了基于状态反馈的协同控制方法;然后推导了闭环系统特征方程,并根据Routh-Hurwitz判据推导了系统闭环稳定性的充分条件,指导控制器参数设计。最后,数值仿真与实车试验结果表明,本文设计的CAV控制器能够有效衰减交通波扰动,提高交通流的平顺性、提升交通流量;而V2V通信时延会加剧交通流误差的峰值,传感器量测时延与之相反。

