简教深学 启智生慧——《单式折线统计图》教学及思考

○周正娟

小学阶段“统计与概率”领域的教学，常常让学生置身于相关的情境中，经历统计的过程，习得统计的技能，积累统计活动的经验，养成数据分析的观念。“单式折线统计图”是学生认识了统计表和单式条形统计图后，学习的一种新的数据表达方式，其重点是“描述数据”。它有什么特点？与已学的统计知识有何关联？它有何统计价值？带着这些问题，我尝试打通知识关联，以简教促深学，帮助学生辩证地认识单式折线统计图。

一、统计数据，打通关联

数学是一门关系学。从“关系”上把握所学知识，厘清知识结构，让单个知识点存储于整体之中，是一种低负担、高质态的学习。本节课教学时，首先让学生整理保温杯不同时刻的水温数据，并用自己的方式描述数据，然后引导学生思考：除了用统计表和条形统计图来记录水温，还有没有其他表达方式？通过呈现3名学生新的数据表达方式，整理出折线统计图。

师：观察这3名同学的作品，各有什么特点？

生：图①用竖线表示水温；图②用横线表示水温；图③用圆点表示水温。（惊喜地在图③上从95依次比画到41）这幅图好有创意，能从中看出点的位置在逐渐下降。

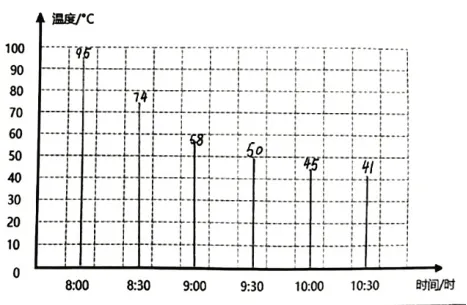
图①

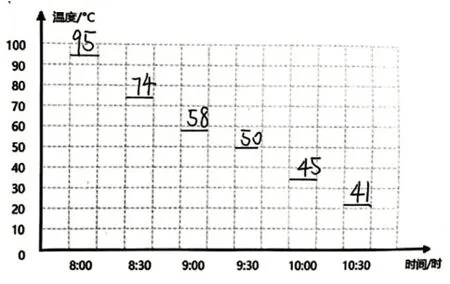
图②

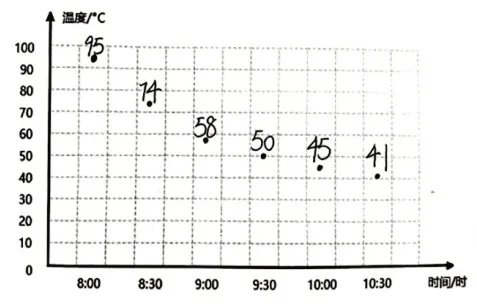
图③

师：是呀，这么一画，点与点就连起来了。（在图③上连点成线）同学们的尝试创造了一种新的数据描述方式——单式折线统计图。它用点表示数量，用线表示数据的变化情况。观察这幅统计图，你能想象出10:30以后水温会怎么变吗？

生：水温还会慢慢下降。

师：是的，数据会“说话”。“点”和“线”的变化情况可以帮助我们分析数据，进行推理。

把折线统计图置于统计知识的整体结构中，让学生明白在统计历程中单式折线统计图是描述数据的一种方式，它用“点”表示数量，用“线”表示变化情况。

二、比较辨析，活化思维

在认识了单式折线统计图后，依然通过温度的变化这一素材来教学。同是温度，保温杯中的水温持续下降，病人的体温有升有降，丰富了折线统计图的形态。同时，通过两幅图的比较、辨析，推动学生展开思考，对折线统计图形成理性认识。

师：两位护士根据同一位病人的体温分别绘制了折线统计图（出示图④和图⑤）。是什么原因造成两幅统计图的折线不一样？

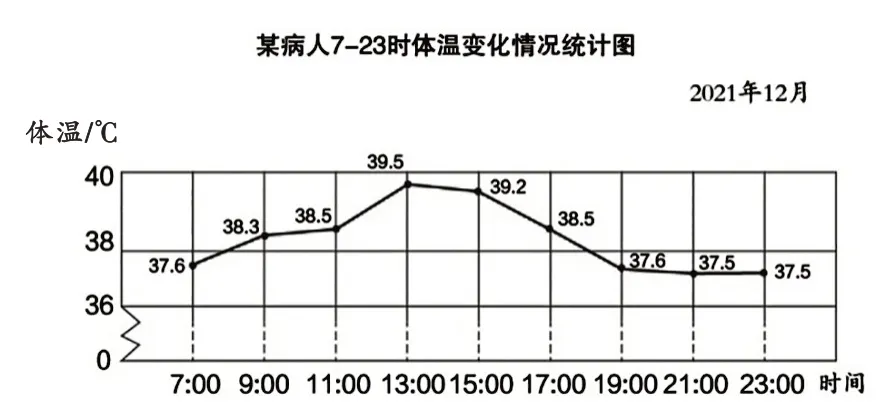
图④

生：（小组讨论后汇报）两幅统计图横轴相同，纵轴每一格表示的温度不一样，造成了两幅统计图中折线的起伏不一样。

师：真是小差异大不同啊！

简单的素材经过合理运用后可以将学习推向深入，根据同样的数据绘制出了不同的折线统计图，认知冲突直逼折线统计图的合理绘图问题。学生在观察、比较、讨论、分析、交流中，进一步感受折线统计图是如何表达数据的，明白纵轴上单位长度的数值对折线统计图形态的影响，洞悉折线的起伏要有数据的支撑才有意义。在这种思维的碰撞中，学生对统计图中信息的把握和理解，从片面走向完整、从表面走向深刻。

三、辩证理解，培育素养

大数据时代，大到国家的宏观政策制定，小到班级三好学生的评选，统计无处不在，良好的数据分析观念逐渐成为人的一种基本素养。不同的现实情境、不同的统计要求，决定了描述数据的方式。

师：图⑥和图⑦都是描述视力情况，为什么选用不同的统计图？

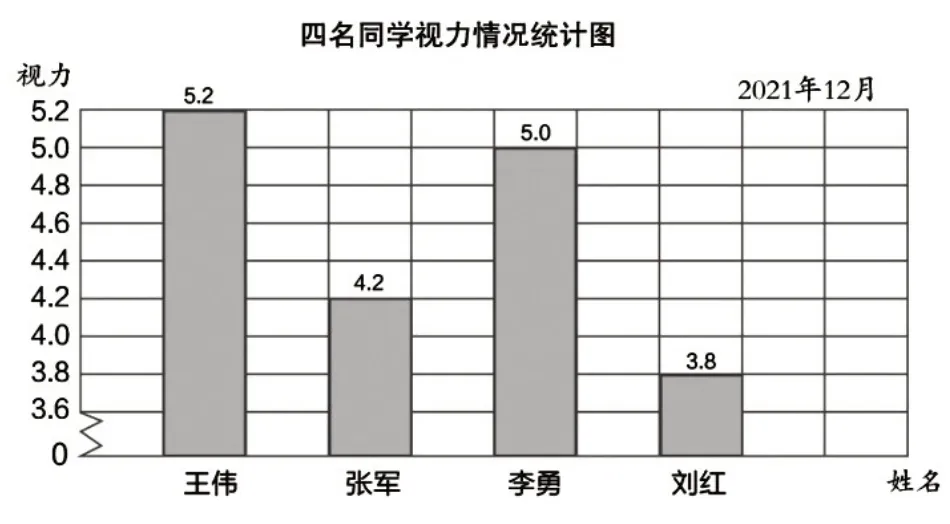
图⑥

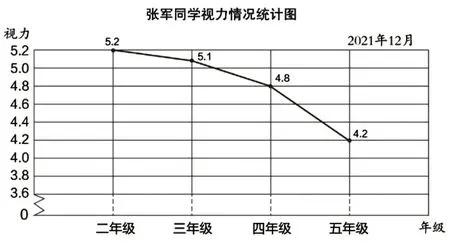
图⑦

生：图⑥是条形统计图，能很好地表示四名同学视力的好坏；图⑦是折线统计图，能很好地表示不同时间张军视力变化的情况。

师：图⑥中不同的直条可以调换位置吗？图⑦中不同的点可以调换位置吗？

生：图⑥中的直条可以调换位置，在条形统计图中只要将姓名和视力的数据对应起来就可以；图⑦中的点如果不按时间顺序排，折线就没有价值了，所以不能随意调换点的位置。

师：各有特点，没有优劣。适合的才是最好的！

出示两幅统计图，让学生思考：条形统计图中的“直条”和折线统计图中“点”可以调换位置吗？这样的设计，不仅让学生对两种数据描述方式进行比较、分析，进一步感受到不同数据描述方式的特点，还引发学生辩证地理解：不同的统计图各有特点，没有优劣，要根据实际情况合理选择数据的描述方式，从而上升到哲学层面的感悟——适合的才是最好的！