Ding-Helleseth-Martinsen序列的交织结构和自相关分布
柯美俭,杨 波,肖自碧
(武汉科技大学理学院,湖北 武汉,430065)
具有最优自相关性质的伪随机二元序列广泛应用于工程领域,如雷达测距、流密码和通信系统等[1]。对于周期为N的二元序列a,根据N模4的剩余,其异相自相关的最优值分为四类[2]:(1)N≡0(mod 4),Ra(τ)∈{0,-4}或{0,4};(2)N≡1(mod 4),Ra(τ)∈{1,-3};(3)N≡2(mod 4),Ra(τ)∈{2,-2};(4)N≡3(mod4),Ra(τ)∈{-1}。满足条件(4)的二元序列称为理想二值自相关序列。此外,若N≡0(mod 4),Ra(τ)∈{0,±4},则二元序列a称为具有最优自相关绝对值的序列[2-4]。
利用交织技术构造最优自相关序列和低相关序列组是序列设计中的一种重要方法。序列的交织结构由Gong[5]于1995年提出,并用于设计低相关序列[4]和序列集[6]。在密码和通信系统中广泛使用的周期为22k-1的m序列、推广的GMW序列都可以采用交织方法构造。2008年,Yu等[4]指出Arasu等构造的几乎差集序列也可以利用交织方法生成。之后,研究者通过选取适当的序列作为列序列进行交织,即重新穿插排列,构造出了一些具有最优自相关性质的新序列[2-3,7]。利用这些序列的交织结构,研究者又发现它们还具有较高的线性复杂度[8-10]以及2-adic复杂度[11-13]。对交织序列的研究不仅有助于构造更多适用于密码和通信领域的新序列(集)以及分析序列的随机性质,而且有助于对序列结构的深入理解,这是序列设计和分析领域的一个十分有意义的课题。
基于中国剩余定理和经典四阶分圆,Ding等[14]构造了两类周期为2p的二元序列(称为Ding-Helleseth-Martinsen序列),p为素数且p≡5(mod 8),其中一类是平衡的,另一类是几乎平衡的。当参数满足一定条件时,Ding-Helleseth-Martinsen序列的异相自相关值为{2,-2}。通过分析该序列的支撑集的特征,本文首先证明其具有p×2交织结构,也就是说,如果将序列的项排成一个p行2列的矩阵,即前两项作为第一行,接下来的两项作为第二行,以此类推,那么该矩阵的两列各自都是经典四阶分圆序列的移位序列或互补序列。在此基础上,本文利用交织序列的自相关公式以及经典四阶分圆序列的相关函数值,计算得到所有Ding-Helleseth-Martinsen序列的精确自相关分布。
1 预备知识
1.1 基本概念和记号
设a=(a(0),a(1),…,a(N-1))是周期为N的二元序列,称集合{t|0≤t 设a=(a(0),a(1),…,a(N-1))是周期为N的二元序列,令L(a)=(a(1),…,a(N-1),a(0)),称L是左循环移位算子。一般地,Lτ(a)=(a(τ),a(τ+1),…,a(τ+N-1)),其中0<τ 定义1[2]设a=(a(0),a(1),…,a(N-1))和b=(b(0),b(1),…,b(N-1))是两条周期为N的二元序列,a和b的互相关函数定义为 (1) 其中t+τ是模N加法。当a=b时,称Ra(τ)为a的自相关函数。 定义2[2]设ai=(ai(0),ai(1),…,ai(N-1))(0≤i u=(a0(0),a1(0),…,aT-1(0),a0(1),…, aT-1(1),…,a0(N-1),…,aT-1(N-1))。 为方便起见,这里用I表示交织运算,记u=I(a0,a1,…,aT-1),称a0,a1,…,aT-1为序列u的列序列。 引理1[2]设u=I(a0,a1,…,aT-1)和v=I(b0,b1,…,bT-1)是两条周期为NT的交织序列,其中ai=(ai(0),ai(1),…,ai(N-1)),bi=(bi(0),bi(1),…,bi(N-1)),0≤i 特别地,当u=v时,有 (2) 定义3[15]设p≡1(mod 4)为素数,g为模p的本原根,设 Di={gi+4j(modp)|j=0,1,…, (3) 称Di为模p的经典四阶分圆类。将支撑集分别为D0∪D1、D0∪D2、D0∪D3、D1∪D2、D1∪D3和D2∪D3以及周期为p的二元平衡序列称为经典四阶分圆序列,分别记作s1、s2、s3、s4、s5和s6,其中s1、s3、s4和s6即为Ding-Helleseth-Lam序列[15],而s2和s5为Legendre序列[16]。 文献[14]中构造了两类周期为N=2p的二元序列,即Ding-Helleseth-Martinsen序列。第一类是几乎平衡的二元序列u,定义为 (4) 其中Cu={0}×C0∪{1}×C1。第二类是平衡的二元序列v,定义为 (5) 其中Cv={0}×(C0∪{0})∪{1}×C1。 定理1设p=4f+1为素数,则对任意(i,j,l),式(4)和式(5)定义的周期为2p的二元序列u和v都具有p×2交织结构,且 u=I(a,L2-1(b)),v=I(c+1,L2-1(b)), 其中a、b和c是周期为p并且支撑集分别为2-1C0、2-1C1和p({0}∪2-1C0)的二元序列。 证明:由于Cu={0}×C0∪{1}×C1,因此序列u的支撑集 {2t+1|2t+1(modp)∈C1} ={2t|t(modp)∈2-1C0}∪ {2t+1|t+2-1(modp)∈2-1C1}。 假设u=I(u0,u1),则有 u1(i)=u(2i+1) 令 则有u1(i)=b(i+2-1),这意味着u1=L2-1(b)。令a=u0,则得到u的交织结构。 且v1(i)=b(i+2-1)。令c(i)=v0(i)+1,即序列c的支撑集为p(2-1C0∪{0}),于是序列v具有交织结构v=I(c+1,L2-1(b))。 注1若2∈De,则2-1∈D-e,因此2-1C0=Di-e∪Dj-e且2-1C1=Dl-e∪Dj-e,也就是说,a和b是支撑集分别为Di-e∪Dj-e和Dl-e∪Dj-e的经典四阶分圆序列。由于i、j和l是{0,1,2,3}中两两不同的整数,因此序列对(a,b)的所有可能选择就是a=sh、b=sk,其中h≠k且h+k≠7。由于c的支撑集为p({0}∪2-1C0)=p({0}∪Di-e∪Dj-e),故c也是六条经典四阶分圆序列之一。若设Di-e∪Dj-e的特征序列为sh,容易验证p({0}∪Di-e∪Dj-e)的特征序列为c=s7-h,则序列对(c,b)的所有可能选择就是c=sh、b=sk,其中h≠k且h+k≠7,其原因是,如果h取遍集合{1,2,3,4,5,6},那么7-h也取遍该集合。 推论1由式(4)和式(5)定义的二元序列u和v分别等价于下面的交织序列: u=I(sh,L2-1(sk))且v=I(sh+1,L2-1(sk)), 其中sh和sk是两条不同的经典四阶分圆序列(见定义3),且h+k≠7。 在接下来的讨论中,为了方便起见,将序列I(sh,L2-1(sk))和I(sh+1,L2-1(sk))分别记作uh,k和vh,k。根据引理1,计算交织序列uh,k和vh,k的自相关分布可以转化为计算它们的列序列sh和sk的相关函数。 引理2设sh和sk为两条不同的经典四阶分圆序列,其中h+k≠7。令τ=2τ1+τ2,其中0≤τ1 Ruh,k(τ)= 和 证明:由τ=2τ1+τ2,根据引理1中的式(2),下面分两种情况讨论。 (i)若τ2=0,0<τ1 Ruh,k(τ)=Rsh,sh(τ1)+Rsk,sk(τ1) =Rsh(τ1)+Rsk(τ1), 再由自相关函数的定义式(1),得 Rvh,k(τ)=(-1)1+1Rsh(τ1)+Rsk(τ1)=Ruh,k(τ)。 (ii)若τ2=1,0≤τ1 Ruh,k(τ)=Rsh,sk(τ1+2-1)+Rsk,sh(τ1+1-2-1)。 由于τ1+1-2-1≡τ1+2-1(modp),故 Ruh,k(τ)=Rsh,sk(τ1+2-1)+Rsk,sh(τ1+2-1)。 再由自相关函数的定义式(1),得 Rvh,k(τ)=-Rsh,sk(τ1+2-1)-Rsk,sh(τ1+1-2-1) =-Ruh,k(τ)。 注2由引理2可得Ruh,k(τ)=Ruk,h(τ)且Rvh,k(τ)=Rvk,h(τ),事实上可以验证uk,h=Lp(uh,k),这表明序列uh,k和uk,h是循环移位等价的,因此只需考虑满足h 为了进一步确定u和v的精确自相关分布,需要借助经典四阶分圆序列相关函数值的结论。 引理3[17]设p≡5(mod 8)为素数且p=x2+4y2,其中x≡1(mod 4)。六条经典四阶分圆序列的自相关函数值以及sh和sk的互相关函数值在表1中给出,这里1≤h 表1 六条周期为p=4f+1的二元序列的相关函数值(f为奇数) 注3当p≡5(mod 8)时,2是模p的一个平方非剩余,因此2∈D1或D3。这里取模p的一个适当的本原根,使得2∈D3,必有y≡1(mod 4)。 下面通过引理2中的公式计算u1,3的异相自相关分布。当τ=2τ1且0<τ1≤p-1时,由表1给出的s1和s3的自相关函数值可得 Ru1,3(τ)=Rs1(τ1)+Rs3(τ1)=-2。 当τ=2τ1+1且0<τ1≤p-1时,则有 Ru1,3(τ)=Rs1,s3(τ1+2-1)+Rs3,s1(τ1+2-1)。 令τ1+2-1=τ′,由引理3可知,对每个τ′∈Di和ω∈Di+2有 Rs1,s3(τ′)+Rs3,s1(τ′)=Rs1,s3(τ′)+Rs1,s3(ω) (6) 由于对每个τ′∈D0∪D2,有ω∈D2∪D0,对每个τ′∈D1∪D3,有ω∈D3∪D1,将表1中给出的互相关值代入式(6),即得式(7): Ru1,3(τ)=Rs1,s3(τ′)+Rs3,s1(τ′) =Rs1,s3(τ′)+Rs3,s1(ω) (7) 于是序列u1,3精确的自相关分布就得以确定。 注意到由引理3有Rs1(τ)=Rs6(τ)、Rs3(τ)=Rs4(τ)且Rs1,s3(τ)=Rs4,s6(τ),因此,根据引理2可得Ru1,3(τ)=Ru4,6(τ),这意味着序列I(s1,L2-1(s3))和I(s4,L2-1(s6))的自相关分布相同。通过类似计算可以确定相应于(h,k)不同取值的其他序列的自相关分布,结果由下面的定理给出。 定理2设p≡5(mod 8)为素数且p=x2+4y2,其中x≡1(mod 4),则周期为2p的交织序列uh,k=I(sh,L2-1(sk)),1≤h 再由引理2知,若τ=2τ1,Rvh,k(τ)=Ruh,k(τ),若τ=2τ1+1,Rvh,k(τ)=-Ruh,k(τ),因此,序列vh,k=I(sh+1,L2-1(sk))的自相关分布可以由定理2的结果得到。 本文证明了Ding-Helleseth-Martinsen序列具有p×2交织结构,进而利用交织序列的自相关公式和经典四阶分圆序列的相关函数值,计算得到了所有Ding-Helleseth-Martinsen序列的精确的自相关分布。计算结果显示,所有Ding-Helleseth-Martinsen序列的异相自相关绝对值相对于其周期都较小,即都具有低自相关性。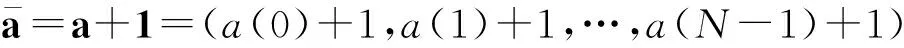
1.2 相关函数
1.3 交织序列及相关函数计算公式
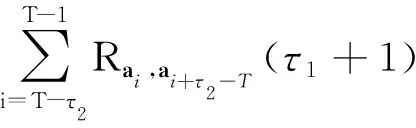
1.4 经典四阶分圆及序列
1.5 Ding-Helleseth-Martinsen构造

2 Ding-Helleseth-Martinsen序列的交织结构
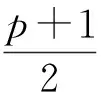


3 Ding-Helleseth-Martinsen序列的自相关分布

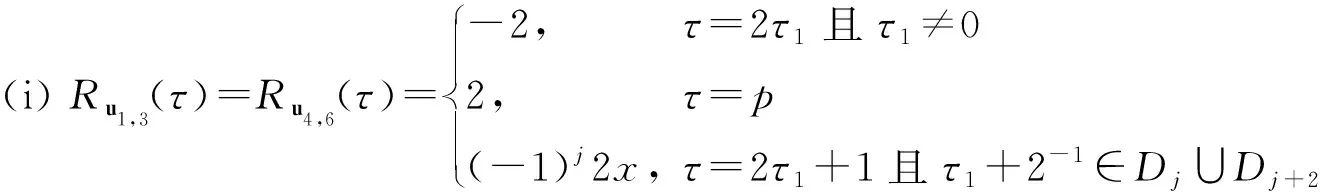
4 结语

