基于动力学约束的动态运动基元机械臂轨迹规划

刘汉东，吴怀宇，郑秀娟，陈 洋

(1. 武汉科技大学冶金自动化与检测技术教育部工程研究中心,湖北 武汉,430081 2. 武汉科技大学机器人与智能系统研究院,湖北 武汉,430081)

随着机械臂技术的飞速发展,机械臂的应用领域已不仅仅局限在工业生产中，在医疗、服务等领域同样有着大量的需求，伴随而来的是机械臂逐渐向轻量化、多自由度、高冗余度的方向发展，这对机械臂的运动功能要求不断提高，也加大了对机械臂轨迹规划的难度[1]。由于机械臂的高维度特性，导致其构型空间的拓扑结构发生根本性变化，进而许多传统的轨迹规划方法不再适用,一定程度制约了机械臂的发展与应用。

从人类学习中发展而来的示教学习机械臂轨迹规划的研究逐渐兴起，示教学习可以指导机械臂实现轨迹规划,从而有效减小了搜寻可行空间的计算量,大大降低了轨迹规划的难度；示教学习也可以赋予机械臂一定的学习能力,机械臂通过模仿学习生成相应的运动行为,获得运动技能,完成特定作业任务[2]。示教学习方法包括动态运动基元(dynamic movement primitives,DMP)[3]和概率运动基元[4]等，DMP算法认为复杂运动可以视为一系列运动基元的叠加，应用DMP算法的系统能够从运动学习的角度将机械臂一次具体运动看作学习样本,提取其运动基元，对于新的目标点，能够利用学习获得的运动基元泛化出相应的轨迹。

机械臂在实际应用中,其周围的环境约束往往处于变动之中，比如突如其来的障碍物、客观因素造成的目标点变动、运动过程中轨迹的偏离等，这些约束可能是由于执行器限制或安全限制而产生的，当运动规划中需要适应这些限制时，运用DMP会使规划的轨迹不可行。Krug等[5]提出了一种模型预测控制方法,该方法能够约束速度,可确保每个自由度的速度保持在允许的范围内,但不能确保路径的形状保持不变；Karlsson等[6]提出了通过降低速度来提高控制器跟踪性能、减小跟踪误差的算法,但降低速度会导致生成路径的变形,因此不能直接用来限制速度或加速度；Weitschat等[7]为了实现机器人的灵活运动,提出了一种使用DMP的泛化方法,动态运动基元被扩展,以保证符合最大速度约束，此方法虽能实现最大速度约束,但没有考虑机器人的加速度约束,也不能实现对障碍物的避障；Koutras等[8]对DMP框架进行扩展,提出了一种由于移动目标而速度增加的抵消方法,但不允许明确的速度限制,且未考虑加速度约束，不能实现对障碍物的避障。

Chi等[9]将动态势场与DMP模型相结合,来实现服务机器人的自主避障功能；Lauretti等[10]提出了一种基于DMP的演示学习方法,使得机器人能够避开路径上的障碍物,在关节空间和笛卡尔空间能够以类似于人类演示的方式进行运动；Ugur等[11]扩展了DMP的框架,增加一个新的非线性成形函数和一个新的力反馈耦合项，利用隐马尔可夫模型参数对动作控制变量的非线性轨迹和执行过程中测得的触觉反馈轨迹进行编码；Ginesi等[12]提出了一个基于超二次位势函数来表示体积的避障框架。以上几种方法虽能实现对简单障碍物的避障,但都未考虑机器人的动力学约束，由此可知，应用动态运动基元算法的场景大都未考虑机械臂的速度和加速度限制，鲜有学者在研究机械臂避障的同时还考虑机械臂的动力学限制，为此,本文针对传统机械臂轨迹规划方法存在适用性差的问题,利用动态运动基元的学习与泛化特性规划出机械臂的运动轨迹，在动态运动基元的基础上,加入改进的耦合项来实现机械臂避障，把对速度及加速度的约束转化为对时间缩放因子的约束,利用改进的更新律来满足机械臂动力学约束,从而提出一种基于动力学约束的动态运动基元避障轨迹规划方法，并通过仿真实验和物理实验来验证该方法的可行性，以期为提升机械臂在不同约束下的轨迹规划能力与环境适应性提供参考。

1 动态运动基元

1.1 动态运动基元原理

动态运动基元的基本思想是向简单且稳定的动态系统引入非线性函数,由非线性函数控制系统的运动过程，最终使系统达到目标吸引子状态。DMP的框架采用带非线性强迫项的二阶弹性系统来描述物体的运动[13-14]。DMP作为一个非线性动力系统，它主要应用于离散和连续两种不同的运动模式，对于离散系统是采用点吸引子系统为基本系统,而对于连续系统采用极限环为基本系统，在这个框架中,物体的运动可以用一组微分方程表示为:

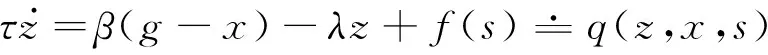
(1)

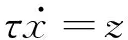
(2)

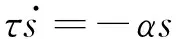
(3)

式(1)为转换系统,其中x为系统的位置,g为系统的目标位置,z为系统的速度,τ为时间缩放因子,用于控制系统的时间缩放；β、λ为系统参数,在选择合适的参数值下,系统会变成一个临界阻尼系统；式(3)为规范系统,其中α为常数,s为相位变量，s是关于时间t的函数,引入相位变量弱化了系统对时间明确的依赖性,任意选择初始状态s0,可以证明s的状态单调收敛于0。

式(1)中强迫项函数f(s)是由径向基核函数通过线性加权形成的,表示为:

(4)

ψi(s)=exp(-hi(s-ci)2)

(5)

式中，ψi(s)为径向基核函数；hi为核函数的带宽；ci为核函数的中心；wi为径向基核函数对应的权重值；i为基函数的数目,示教轨迹越复杂,需要的基函数就越多。

为了实现轨迹的学习及规划,需要建立示教轨迹与新生成目标轨迹之间的联系,即通过观测学习样本为强迫项函数提供权重值wi。参数wi的学习可以通过局部加权回归来完成，之所以选择局部加权回归,是因为它的一次性学习过程非常快,而且各个内核的学习相互独立。

记录一维的示教运动,设整个示教运动的轨迹可以用一组位移、速度和加速度的连续序列表示,将示教运动作为样本带入公式(1)中,得到非线性项为:

(6)

要想完成学习任务,需要找到合适的权重wi。首先将公式(6)中f(s)demo逼近真实样本模型的强迫项函数f(s),把公式(4)改写成线性方程的形式为:

f(s)=Tw

(7)

(8)

w=[w1…wn]T

(9)

然后通过最小二乘准则来求出权重wi的值,即：

(10)

当J取最小值时的wi就是该系统所对应的最佳权重值,在此基础上,利用计算得到的最佳权重值拟合出运动学习时的位移、速度和加速度值的序列,从而完成学习的过程。若改变物体运动的目标点,DMP能够利用已经学习的权重,反向拟合出新的运动特征序列,规划出一条运动轨迹,从而实现泛化推广的过程,此运动轨迹有与原学习轨迹相似的运动特征。

利用动态运动基元算法进行机械臂轨迹规划分为三部分,包括运动分解与特征提取、轨迹学习、轨迹泛化,其流程图如图1所示。

图1 基于DMP的机械臂轨迹规划流程图

将上述一维的动态运动基元模型通过不同维度上的组合,可以构成二维平面或三维空间中的运动,从而可以产生复杂的运动轨迹。对于多维度的情况,规范系统是共享的,而每个维度都有独立的非线性函数和转换系统。

DMP算法的特点是可通过学习参考轨迹的运动信息并对新目标进行泛化,使新生成的轨迹具有与原轨迹相似的运动趋势,并保证收敛到目标状态，同时DMP算法还具有时间项和空间项缩放的优点。

1.2 改进的避障耦合项

机械臂一次完整的作业运动可作为一个学习样本,机械臂对此样本的学习可进行不同目标的自主泛化，但DMP的学习特性使得泛化结果会保留样本的某些特征,例如轨迹的凹凸性,所以不同的样本对应各自的泛化结果，由此可见，DMP算法对于运动的目标、起始点、持续时间的变化是具鲁棒性的。

将DMP算法应用在机械臂的轨迹规划上,除了到达目标点完成作业任务外,尤其重要的一点是运动过程中能否避开障碍物,即是否能够根据先验知识或传感器返回信息完成对轨迹的修改。当机械臂运动的环境中存在障碍物时,原DMP算法规划的轨迹不能完全适用。Khatib[15]将物理学中“场”的概念引入机械臂的运动规划中,在机械臂工作环境中建立人工势场，该势场由目标点产生的吸引势场和由障碍物产生的排斥势场组成，机械臂在势场产生的合力作用下朝着目标进行无碰撞的避障运动；Fajen等[16]发现了一种模拟人类避障的微分方程,通过数学表达式来实现避障,并指出目标对转弯速度的影响随着其与运动方向的夹角增大而指数增大,随着距离的增大而指数减小；Hoffmann等[17]在原DMP模型的基础上加入运动特征与障碍物的耦合项,使运动轨迹发生变化,将其拓展为具有避障功能的运动规划系统：

(11)

Ct=Rμzηexp(-δη)

(12)

(13)

式中，Ct为加入的耦合项；o为障碍物位置；x和z分别为机械臂的位置和速度；η为速度向量z与障碍物中心位置和机械臂当前位置坐标差向量(o-x)的夹角；μ、δ为系统常数；R为旋转矩阵,决定避障轨迹绕障碍物的旋转方向。

利用动力系统对扰动的鲁棒性来避障，耦合项作为到障碍物的距离矢量函数,相当于增加了垂直于当前速度方向的运动,使运动轨迹远离障碍物。式(12)中的耦合项对近距离的障碍物和远距离的障碍物赋予同样的地位,这可能导致运动轨迹的振荡行为，同时，加入耦合项的动态运动基元算法虽可以避障,但学习后的轨迹与样本轨迹有较大误差,不利于机械臂安全地完成作业任务。

针对以上的不足之处,对避障耦合项进行改进。为了确保改进模型的全局稳定性,引入S形状的logistic函数为:

(14)

式中，m为曲线某一点的坐标；m0是曲线中点；L代表曲线的峰值；b为曲线的陡度。

假设障碍物的速度为vo，将h(x)加入后,改进后的耦合项为:

(15)

(16)

由此可见，针对动态障碍物,避障耦合项需要考虑的因素不再是机械臂本身的运动速度,而是机械臂和障碍物之间的相对速度(z-vo)。

2 速度及加速度约束

2.1 速度约束

不考虑动力学限制会使移动机械臂或机器人在执行任务时违反安全限制或电机的转矩限制,可能造成安全事故、损坏移动机械臂或机器人,所以有必要考虑系统轨迹的速度和加速度约束。要确保机械臂在与人类交互时能够安全地执行任务,则要在机械臂的位置和速度随时间不断变化的环境中提供安全交互的框架,约束DMP系统轨迹的速度和加速度分别为:

(17)

(18)

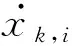
由公式(2)和公式(17)推导得到:

(19)

由于轨迹速度与时间缩放因子τk成正比,因此对系统轨迹速度的进一步预测是可行的,可以将速度约束转化为对时间缩放因子τk的约束，即：

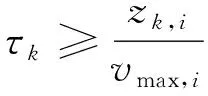
(20)

2.2 加速度约束

对公式(2)两边求导得到:

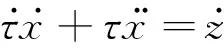
(21)

进一步推导得到:

(22)

加速度由当前的时间缩放因子及其导数来决定,要使加速度约束能够满足,要求公式(18)成立,经过推导得到:

(23)

(24)

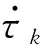
2.3 改进的基本更新律

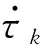
(25)

(26)

上述基本更新律虽然能够使速度和加速度在连续时间情况下保持在规定范围内,但是生成的轨迹曲线不够平滑,加速度在某些地方有突变，这不利于实际的机械臂运动轨迹控制，甚至有时τk的极端变化会导致物体的运动轨迹不可行。

针对这些缺点,对原来的基本更新律进行改进,改进之后的基本更新律为:

(27)

(28)

改进的基本更新律包括两个部分，一部分作为势函数,其目的是在加速度接近极限时,通过增加τk将加速度保持在约束之内；另一个部分的作用是驱动τk回到标称的时间缩放因子τ*。当加速度都离约束足够远时,公式(27)中的势函数项可以忽略不计,基本更新律可以解释为一阶滤波器。

使用改进的基本更新律,轨迹加速度在达到极限之前被减慢,因此可能导致略慢于所需的轨迹加速度，然而,这种处理加速度限制的保守方法为饱和控制器中的反馈项提供了更多容量,可以提高控制器的跟踪性能。改进的基本更新律可以使所有维度的轨迹以及相位以同步的方式被延迟,路径保持不变。

3 实验与结果分析

本文主要研究的是机械臂在二维平面下的运动场景，其运动可以分解为X1和X2两个方向的运动。采用高阶多项式生成训练轨迹样本，高阶多项式所生成的轨迹及其一阶、二阶导数分别对应机械臂末端执行器做运动所需要的位移、速度及加速度。根据DMP算法进行实验设计,在Matlab中设计仿真实验,再进行物理实验。

3.1 避障前后对比仿真

在Matlab的机器人工具箱搭建一个三自由度机械臂的平台。首先在没有障碍物的情况下,利用DMP的学习与泛化特点规划出一条运动轨迹,然后在机械臂运动的平面中加入两个静态障碍物,验证其自主避障功能，然后利用改进的耦合项来进行避障实验。静态障碍物避障运动轨迹曲线对比如图2所示。图2中黑色圆代表大小不同的两个静态障碍物，从图2中可以看出,在有障碍物的情况下,机械臂通过加入耦合项的动态运动基元算法能够规划出一条可行的避障轨迹,且避障轨迹平滑，同时还可以看出，避障耦合项改进前后的机械臂均可进行避障,表明DMP系统具有良好的学习能力与泛化能力。

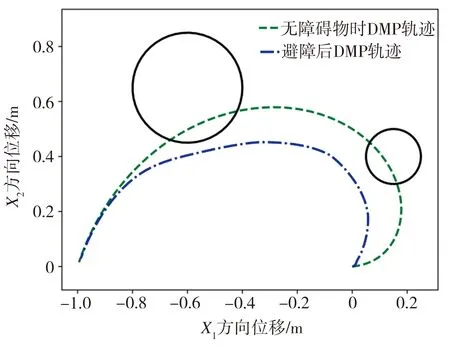
(a)改进前

(b)改进后

通过改变静态障碍物的大小,做20组不同的避障实验，分别计算每一组避障耦合项改进前后机械臂规划的避障轨迹与样本轨迹的误差,求取每一组轨迹误差的平均值，并把计算的20组平均值求和之后再计算均值,并根据此均值计算轨迹误差的方差及标准差,避障耦合项改进前后静态障碍物避障轨迹误差如表1所示。从表1中可以看出,与利用原避障耦合项规划的轨迹相比,避障耦合项改进后的避障轨迹与样本轨迹的误差均值更小,轨迹误差的方差及标准差均较小,由此表明，避障耦合项改进后的总体轨迹误差较小,利用改进的避障耦合项在完成避障的同时能够尽量保持与原始轨迹的一致性。

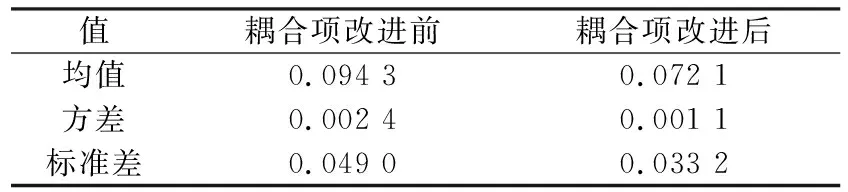
表1 避障耦合项改进前后静态障碍物避障轨迹误差

将机械臂运动的平面中两个静态障碍物换成一个动态障碍物后再进行实验，避障耦合项改进前后动态障碍物避障运动轨迹曲线对比如图3所示。图3中黑色箭头表示动态障碍物的运动方向,此动态障碍物的运动速度设定为0.19 m/s，实线圆表示动态障碍物开始运动的位置,虚线圆表示动态障碍物运动过程中的位置。从图3中可以看出，改进后的避障耦合项生成的运动轨迹可以避开动态障碍物(见图3(b)),而利用原始避障耦合项生成的运动轨迹与动态障碍物会相交,不能避开动态障碍物(见图3(a))，由此可见，利用改进的避障耦合项可以完成对动态障碍物的避障,表明避障耦合项改进后的系统具有良好的避障规划能力与环境适应性。

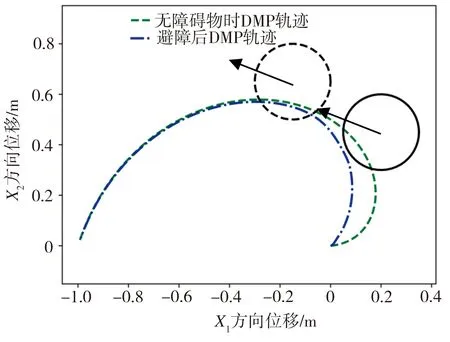
(a)改进前

3.2 速度约束前后对比仿真

机械臂末端执行器在二维平面下的运动分解为X1和X2两个方向上的运动,相位变量s是关于时间t的函数,为了简化比较,在横坐标轴上使用的是相位变量,而不是时间变量。在机械臂规划的运动轨迹能够实现静态障碍物避障的基础上,考虑加入速度限制,X1和X2两个方向的速度约束绝对值分别设为0.15、0.18 m/s。

速度约束前后系统轨迹速度曲线对比如图4所示。在实验的开始,并没有设置速度约束,在相位变量s=0.8时,加入了速度约束。从图4中可以看出,未使用基本更新律的DMP系统轨迹速度会超过限制；当使用所提出的基本更新律时,系统在两个方向上的速度能够满足约束,能够适应在线修改的速度限制,并且在其余部分会遵守新的速度限制。

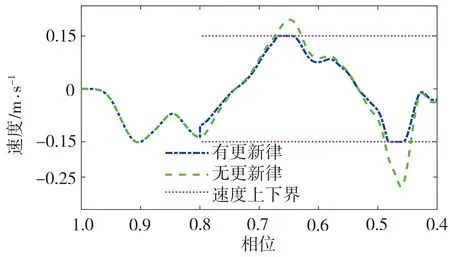
(a)X1方向

3.3 加速度约束前后对比仿真

在机械臂规划的运动轨迹能够实现静态障碍物避障的基础上,考虑加入加速度限制,对X1和X2两个方向的加速度限制的绝对值分别设置为0.27、0.26 m/s2，加速度约束前后系统轨迹的加速度曲线对比如图5所示。从图5中可以看出,施加运动轨迹的加速度约束后,利用基本更新律的DMP系统在达到加速度限制之前主动缩放轨迹,加速度保持在整个界限内,而未使用基本更新律的DMP系统会违反加速度的限制,加速度超越了上下界线。

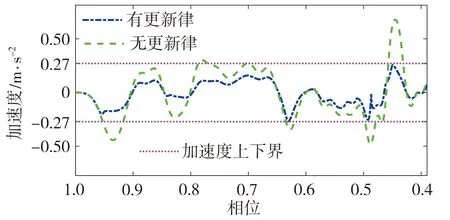
(a)X1方向

3.4 基本更新律改进前后对比仿真

在机械臂规划的运动轨迹能够实现静态障碍物避障的基础上,考虑加入加速度限制,对X1和X2两个方向的加速度约束不同，X1和X2两个方向的加速度限制的绝对值分别设置为1.05、0.88 m/s2。改进的基本更新律并没有在极限处大幅度改变τk,而是随着接近极限而逐渐增加τk，也就是说,当接近极限时,通过选择τk,运动轨迹速度都会以一种预防的方式减慢，该方法可以通过主动缩放而不是单纯的反应性缩放来保持对更大范围轨迹的微分约束的可行性,从而能够更大程度地满足约束。更新律改进前后系统轨迹的加速度曲线对比如图6所示。从图6中可以看出，与原来的基本更新律相比,改进的基本更新律在约束系统加速度的同时,加速度曲线更加平缓,波动较小。

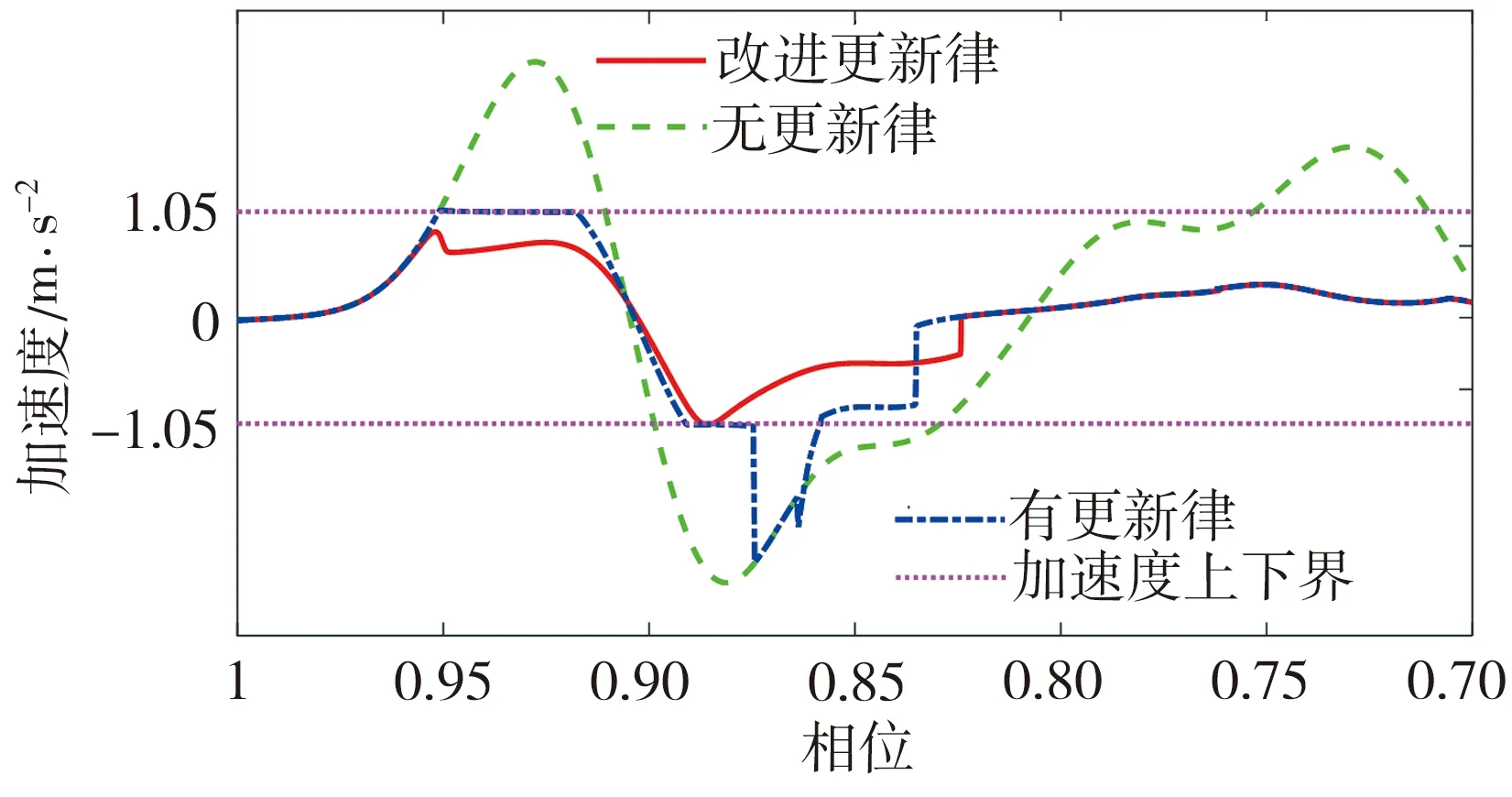
(a)X1方向

更新律改进前后加速度峰值如表2所示。从表2中可以看出,利用改进后的基本更新律得到的DMP系统的加速度峰值比改进前的加速度峰值小,其加速度曲线更加平缓。由图6和表2可以看出,基本更新律改进后不仅使加速度约束更容易满足,也能获得更平稳的加速度,同时保持生成的轨迹曲线与参考轨迹具有良好的轨迹跟踪特性。

表2 更新律改进前后加速度峰值

3.5 避障轨迹规划物理实验

将以上仿真分析的系统集成在一个三自由度的移动机械臂平台上,在移动机械臂上进行真实环境下的实验。移动机械臂的上位机使用机器人操作系统(robot operating system,ROS)通信,下位机运动控制卡通过PWM控制机械臂运动。机械臂示教学习及避障过程如图7所示。首先在没有障碍物的情况下,利用DMP的学习与泛化特点,使移动机械臂规划出一条运动轨迹,如图7(a)～图7(c)所示；随后在环境中加入静态障碍物后重新进行自主轨迹规划测试，在机械臂的正下方放置一个圆形凳子作为静态障碍物,如图7(d)～图7(f)所示。在实验中加入速度限制,X1和X2两个方向的速度约束绝对值分别设为0.15、0.18 m/s,利用改进的耦合项来进行避障试验。移动机械臂进行自主避障规划的轨迹曲线如图8所示,图中圆表示障碍物。从图7和图8中可以看出,在没有障碍物的情况下,移动机械臂在起始位置开始,从左边运动至右边,到达目标位置；在有静态障碍物的情况下,移动机械臂的运动轨迹平滑且能避开障碍物完成实验任务,验证了所提出的轨迹规划方法的有效性,表明了该系统具有一定的避障规划能力与环境适应性。

(a)示教运动开始 (b)运动至中间 (c)示教运动结束

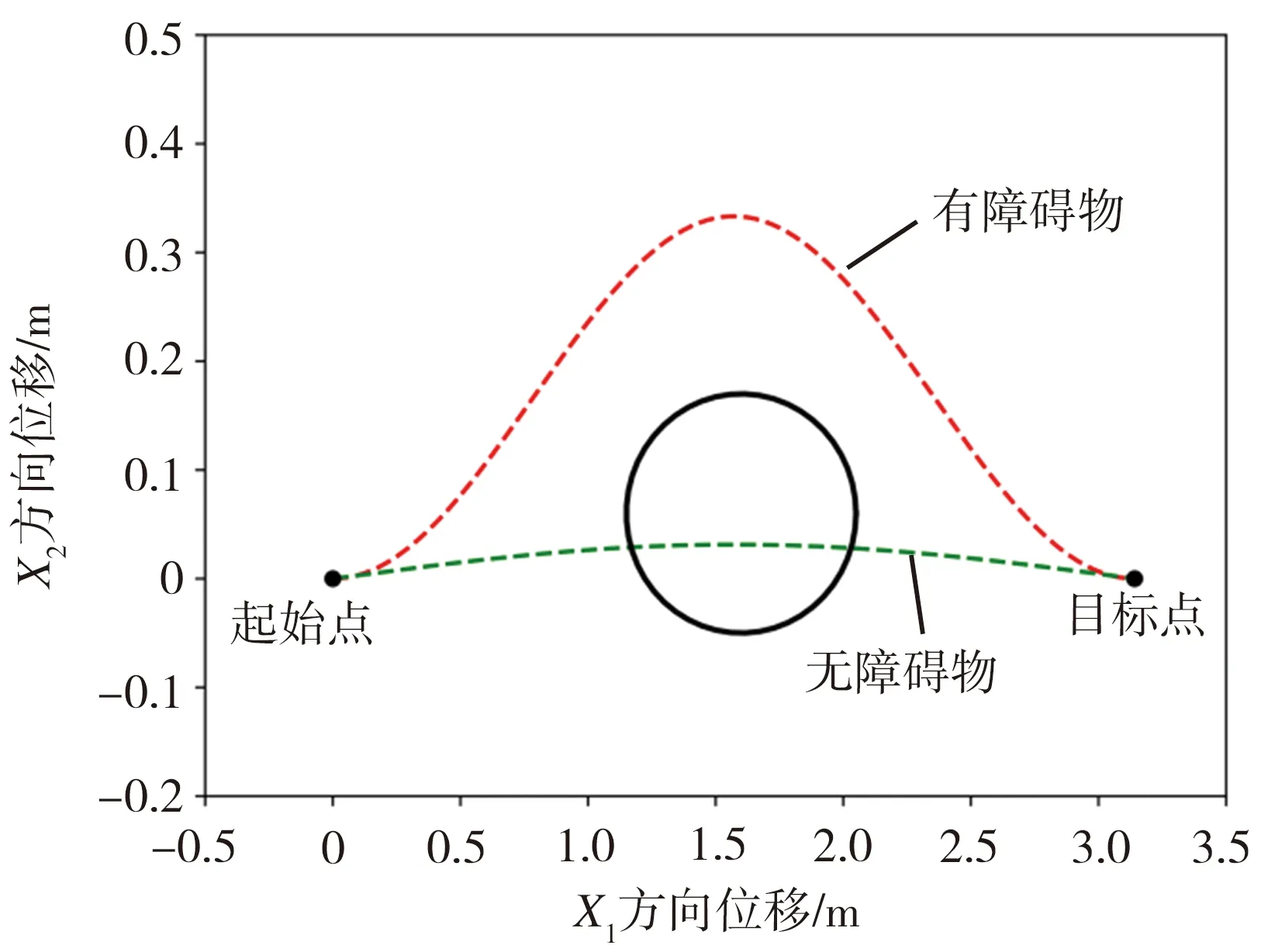
图8 机械臂避障轨迹曲线

4 结语

(1)利用动态运动基元的学习与泛化特性规划出机械臂的运动轨迹，用改进的耦合项来实现机械臂避障，把对速度及加速度的约束转化为对时间缩放因子的约束,利用改进的更新律来满足机械臂动力学约束，提出一种基于动力学约束的动态运动基元机械臂轨迹规划方法。

(2)基于动力学约束的动态运动基元机械臂轨迹规划方法能够使机械臂在避障的同时,遵守速度或加速度约束,并且速度约束可以在线修改。

(3)与传统机械臂轨迹规划方法相比,基于动力学约束的动态运动基元机械臂轨迹规划方法可以提升机械臂在不同约束下的轨迹规划能力与环境适应性。