基于CFD的海洋污底和防污涂层壁面阻力特性影响分析

漆 超，吕续舰

(南京理工大学 能源与动力工程学院，南京 210094)

船舶阻力对船舶航行至关重要，直接影响到船舶的速度、功率和燃油消耗等.船舶阻力可分为摩擦阻力和剩余阻力两类.对于常用的商船，船体表面摩擦阻力占总阻力的约70%[1].由于95%的货物是通过海上运输的，减少摩擦阻力将有效降低船舶运行燃料消耗，从而减少全球的碳排放.

引起船舶阻力增加的因素有很多，而海洋污底生物附着是引起船舶污底阻力变化的重要因素之一[2].生物污底包括“微生物、藻类、植物或动物在潮湿表面上的沉积和生长”[3].其具有3个主要的负面影响：增加阻力、由于阻力的增加引起的燃料消耗的增加、对底层漆膜的损伤和侵入性水生物种的转移[4].目前，最有效、最经济、应用最广泛的生物污底预防方法是应用防污涂层技术[5].

关于污底和防污涂层对船舶航行阻力的影响，国内外学者都对此进行了系列研究.文献[6]以某交通艇为试验对象，分析了船舶污底对其航行性能的影响；文献[7]基于CFD方法分析了粗糙度和污损对船舶阻力的影响；文献[8]建立了最适合于涂层的粗糙度函数模型，预测了防污涂层对全尺寸平板摩擦阻力的影响；文献[9]采用纳米压痕技术，给出了几种防污涂料的力学性能与防污性能的相关性；上述研究大多为定性研究，因此文中将着重于定量研究.

目前，CFD方法以其成本低、周期短等优势得到快速发展及广泛应用[10].当前针对海洋污底和防污涂层对船舶阻力的影响多数为定性分析，且对污底附着引起的流动特性改变少有研究.因此，针对污底和防污涂层对具有相对简单几何形状的海洋装置的表面阻力特性问题，选取两种典型模型NACA-4424翼型和SUBOFF潜艇，采用CFD方法对不同工况下污底和防污涂层的增阻效果进行定量分析，初步给出壁面污底增阻随污底程度的变化趋势，明确防污底涂层对壁面阻力的影响.同时对不同污底附着工况下近壁面流动特性开展研究分析，分析污底增阻机理，为船舶污底阻力的降低提供有益参考.

1 计算模型与数值方法

1.1 计算模型

图1为NACA-4424翼型，其详细尺寸和主要污底粗糙度参数如表1.

图1 NACA-4424翼型

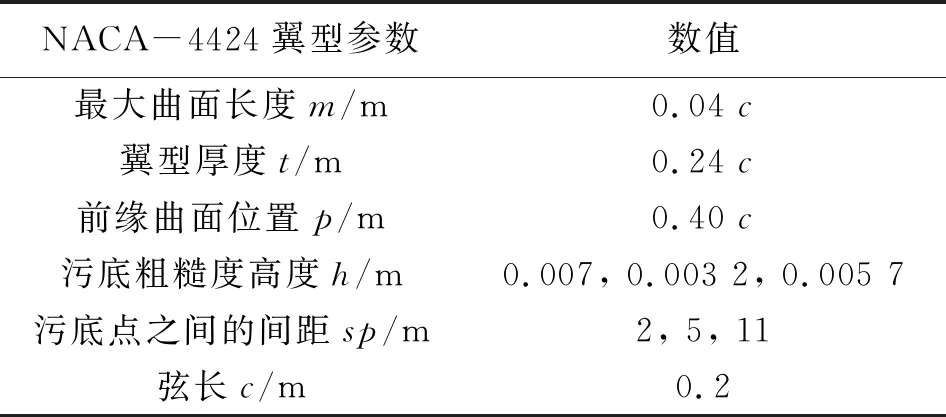
表1 NACA-4424详细信息

SUBOFF潜艇模型已广泛用于水动力分析中，常用的有AFF-1(不带附体)和AFF-8(带附体)2种基本模型，文中采用带有附体的AFF-8模型开展数值计算.图2和表2分别给出了该模型的三维模型和主要参数[11].

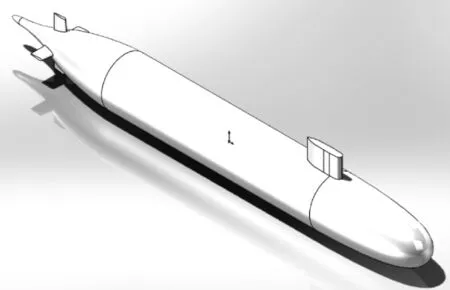
图2 AFF-8潜艇模型

表2 SUBOFF AFF-8潜艇模型的主要参数

1.2 污底和防污建模

1.2.1 污底模型

由于污底模型建立的复杂性，仅对二维机翼模型进行污底模型建模，三维潜艇模型不予考虑.为定量反映壁面污底程度，通过在翼型表面上设置小锥形体来近似模拟污底，如图3.计算中的污底设置如表3.

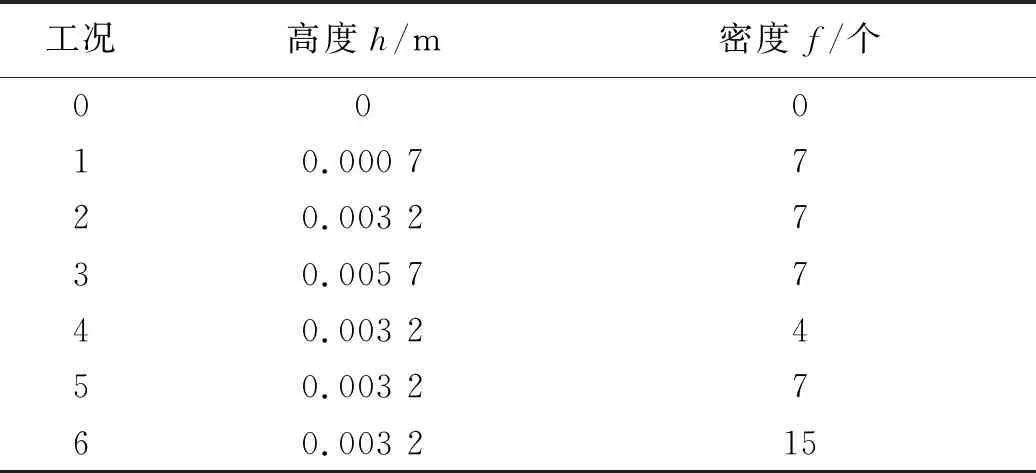
表3 计算污底粗糙度设置情况

由于底的粗糙分布建模难度较大，因此采用简化的二维翼型进行粗糙建模，将翼型上下边分别均分为50份，每份的长度为l，每两个凸起之间的距离相同且为l的整数倍.同时为避免较难计算处理的近壁流动情况，在后缘和前缘未设置粗糙凸起.具体污底粗糙参数如表3，当凸起间距一定时，工况1、2和3对应不同粗糙高度的情况；当粗糙高度一定时，工况4、5和6代表不同粗糙密度的情况；工况0代表表面没有污底的光滑翼型.

1.2.2 防污模型

为了减缓污底生长速度，可在壁面涂覆防污涂层.壁面涂覆防污涂层后，其表面粗糙度会发生变化，此时可采用粗糙度高度来建立涂层的几何计算模型[12].首先引入粗糙度参数h，定义为：

h=RaΔa/2

(1)

式中：Ra为中心线平均粗糙度高度；Δa为绝对斜率.

在商用CFD软件Fluent中，可通过sand-grain粗糙度函数ks来实现壁面粗糙度的设置[5]，其中粗糙度高度和粗糙度函数存在关系：

(2)

式中：Cs为粗糙度常数，通常可取0.5[4].

ks值也取决于模型的特征长度L和流动雷诺数Re，可用文献[13]的方程来解释，具体为：

(3)

文中使用了3种防污涂层系统：硅酮涂层，自抛光共聚物涂层(SPC)和三丁基锡涂层(TBT).根据文献[14]的经验，取防污表面的粗糙度高度为0.17Ra，得到3种涂层的粗糙度参数，如表4.

表4 几种防污涂层的粗糙度及计算ks值

1.3 数值方法

1.3.1 湍流模型

文中基于N-S方程，求解两种简单几何模型，绕机翼流动基于弦长的雷诺数为4.8×105，绕潜艇的流动雷诺数为1.3×107.显然，二者均需采用湍流模型予以求解.标准k-ε方程是常用的双方程湍流模型，它在解决自由剪切流问题方面具有优势，但在解决近壁流动问题时存在一些缺陷；标准k-ωSST模型能更准确地求解近壁流动问题，且对远场流动也能得到较好的计算结果.在文中，对于翼型模型选用标准k-ε方程，同时采用标准壁面函数改善近壁流动处理；对于潜艇模型，其近壁流动较为复杂，采用了标准k-ωSST模型进行处理.

1.3.2 网格划分及边界条件

翼型流体域由半圆形域和矩形域组成，同时在计算域内的翼型周围设置一个半径为2.5c的加密区，加密区内采用非结构网格以便更好的捕捉翼面上污底凸起，加密区外设置为结构网格以节省计算资源.以迎角15°、中等污底高度和密度工况为例划分计算网格(图4)，其中左边半圆加上下两边为入口边界，最右边竖直边为出口边界.

图4 机翼和网格

潜艇模型计算域为长方体域，潜艇前端距离计算域入口边界1.5LPP，潜艇后端距出口边界5LPP，上下左右壁面与潜艇中心的距离为2LPP.采用非结构网格进行划分，同时在附体和艇体周边进行局部网格加密以提高计算精度，潜艇模型网格如图5.

图5 潜艇模型的计算域和网格

对于机翼模型，入口边界设置为速度入口，出口边界设置为压力出口，圆形域与外域之间设置为interface.在污底情况下，翼型的壁面边界设置为无滑移表面；在防污情况下，机翼的壁面边界同样设置为无滑移表面，但此时要根据涂层参数设置Sand-Grain Roughness参数.对于潜艇模型，假设潜艇完全淹没在无限流域中，其表面设置为无滑移表面，计算域的入口和出口设置与翼型相同.流域其余部分均设置成对称边界Symmetry，以尽可能降低边界效应.采用定常计算方法，动量和湍动能项采用二阶迎风格式进行离散，选择对混合网格更为有效的Green-Gauss节点梯度选项，对于翼型和潜艇两种模型均采用SIMPLE算法开展计算.

2 数值验证和分析

2.1 网格无关性验证

通常认为，第一层网格高度必须足够小，才能更好的捕获湍流.对于大多数湍流模型，Fluent适用的y+在30～300.同时，网格总数也是影响计算精度的重要因素.

2.1.1 NACA-4424翼型网格无关性验证

图6为不同y+下NACA-4424翼型阻力系数CD的变化.对于NACA-4424翼型，将y+减小到100后CD值趋于稳定，继续减小y+基本不会影响结果，因此后续计算y+取100.在此基础上，4种不同网格数下的进行计算结果如图7，当网格数大于7×105时，阻力系数随着网格数的增加变化不明显，即此时网格数已经收敛.

图6 y+对应翼型表面阻力系数的变化

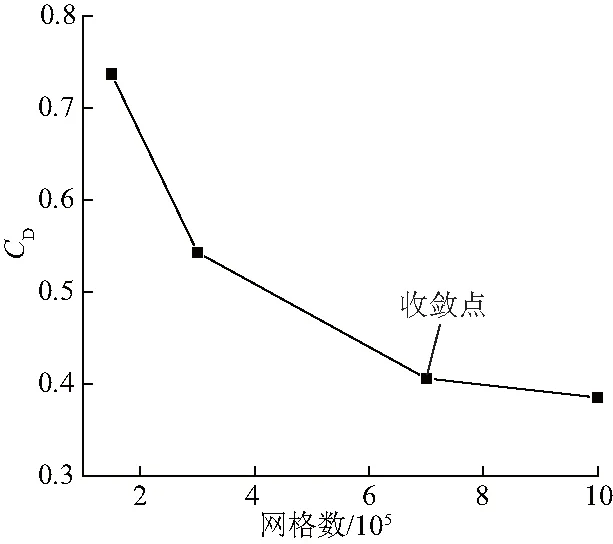
图7 y+=100时，网格数对应翼型表面阻力系数的变化

2.1.2 潜艇模型网格无关性验证

对于潜艇模型，由图8可以观察到，当y+小于130左右时，阻力系数收敛良好.当y+为130时，网格数会更少，因此取y+为130开展后续计算分析.由图9可以得出，当网格数大于5×105时，继续增加网格数对结果影响基本可以忽略，此时认为网格数已经收敛.

图8 y+值对应潜艇表面阻力系数的变化

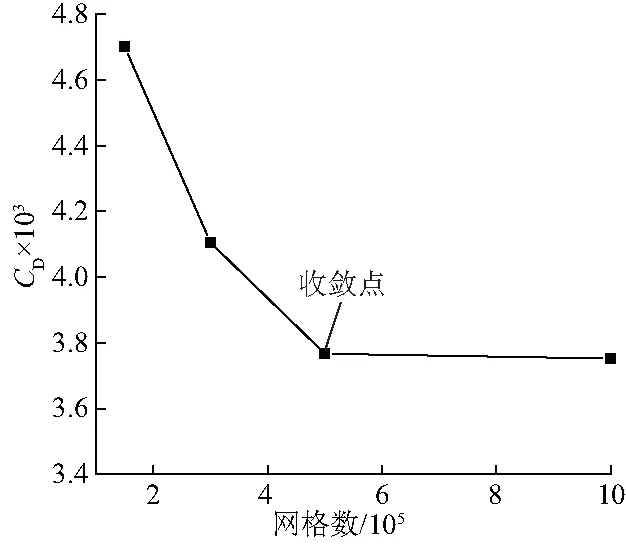
图9 y+=100时，网格数对应潜艇表面阻力系数的变化

综上所示，文中后续针对NACA-4424翼型的计算分析可采用y+为100、网格总数为7×105的计算网格，针对SUBOFF潜艇模型的计算分析可采用y+为130、网格总数为5×105的计算网格.

2.2 污底阻力特性分析

对于不同的结垢水平，升力系数CL与阻力系数的比值(CL/CD)随迎角α变化如图10(基于污底高度h)和图11(基于污底密度)，sp为每两个结垢点间的间距，为l为整数倍.图10、11中不仅给出了数值模拟的升阻比值，同时给出了相关文献实验参考值[4].将数值模拟结果与实验结果进行对比，发现光滑壁面条件下计算结果与实验结果存在一定偏差，计算值略高于实验值，主要原因是简化的计算模型忽略了翼型头部和尾部处的污底，且实验中不可能实现壁面的完全光滑，同时存在一些外界因素干扰，因此导致升阻比偏小.由于计算与实际过程不可避免的存在偏差，因此在计算结果偏差不大的前提下，发现升阻比变化趋势基本相同，可认为数值模拟计算结果与文献实验结果吻合较好，即建立的数值模型是合理可行的.

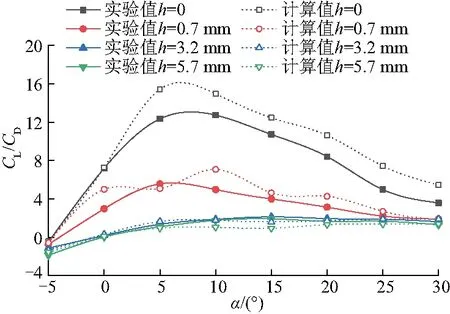
图10 翼型在不同迎角下的升阻比(基于污底高度)

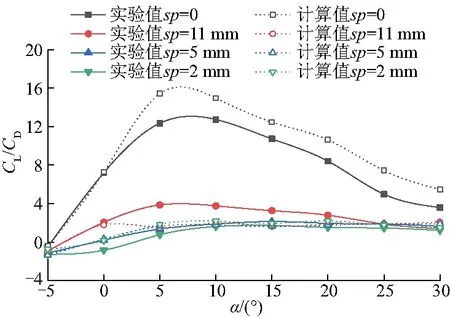
图11 翼型在不同迎角下的升阻比(基于污底密度)

对图10进一步分析可得，随着结垢高度的升高，CL/CD明显变小，且在污底高度较低时，变化量较大，在污底高度较高时，变化量逐渐变小.结合图12不同迎角α下翼型升力和阻力系数变化可得，翼型表面升力和阻力受污底高度影响较大，随污底高度的增加翼型升力减小而阻力增大，即升阻比与污底高度呈反比.且来流攻角小于10°时翼型升力系数变化率大于阻力系数变化率，因此随攻角的增大翼型升阻比先增大后减小.

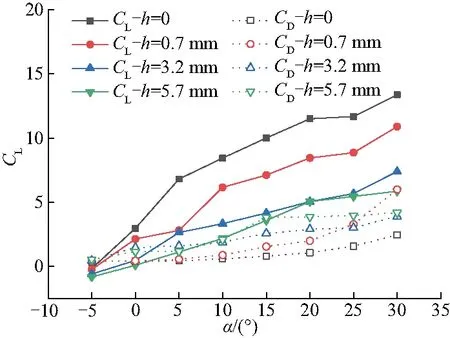
图12 翼型在不同迎角下的升力系数和阻力系数变化(基于污底高度)

由图11、13可以发现，在中等污底高度下随着污底密度的增大，翼型升力减小而阻力增大，即升阻比减小，但是在不同的污底密度下差异并不显著.引起以上变化的主要原因是污底的存在导致来流在翼型表面发生流动分离，而污底的高度越高，相应的流动分离也越剧烈；污底的存在通常使流动分离现象发生在翼型头部附件，当产生流动分离以后，在流动分离点以后的污底对其流动分离程度影响较小，因此不同污底密度下的升阻比变化量较小.

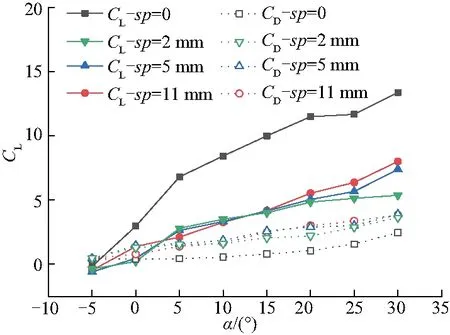
图13 翼型在不同迎角下的升力系数和阻力系数变化(基于污底密度)

当迎角为15°时，不同污底高度和污底密度的速度云图(x方向速度)如图14、15，坐标x,y表示翼型的相对位置及尺寸.从两图可得，当翼型表面不存在污底时，流动分离发生的比较晚，近壁区域多为速度梯度较高，此时翼型表面阻力较小；当翼型表面存在污底时，针对不同污底高度h下的流动分离情况，当污底高度增大时，流动分离发生的较早，近壁区多为低速区，此时翼型表面阻力显著增大.

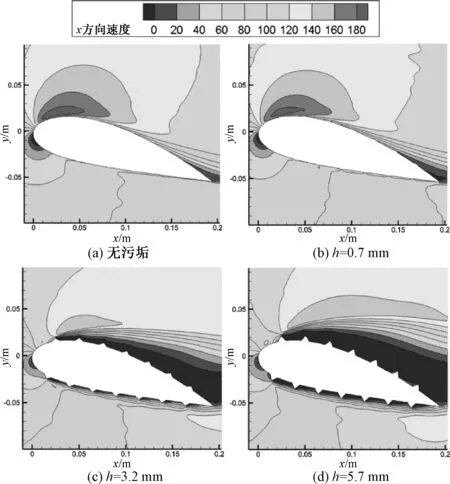
图14 不同污底高度下x方向速度云图

即随着结垢高度的增加，流动分离点会向翼型前缘移动，污底高度越大流动分离现象越明显，且表面阻力越大.针对不同的污底密度下的流动分离情况，发现3种污底密度下流动分离区域相差不大，即其阻力特性相似，与方向速度计算结论相同.

当迎角为15°时，不同污底高度和污底密度工况下翼型表面压力分布如图16、17.可以发现，由于污底的存在，翼型表面发生了流动分离，使上表面压力梯度明显升高，此时阻力显著增加.

图16 不同污底高度下翼型表面压力分布

图17 不同污底密度下翼型表面压力分布

对于不同的污底高度，随着污底高度的增加，压力梯度呈递增趋势，同时流动分离点向翼型前沿移动，流动分离区域更加明显；对于不同的污底密度，压力梯度、流动分离区域相差均不大，但是随着污底密度的增加流动分离点更易观察且向前沿移动.与速度分布给出的变化趋势与结论基本一致.

当迎角为15°时，不同的污底高度和污底密度下翼型表面湍动能分布如图18、19.由图18可以看出，在翼型表面附近湍动能k随着结垢高度的增加而增大，且在污底高度较低时湍动能增加更显著；同时上表面流动分离区域也随之增大，下表面出现流动分离，变化趋势与上表面相同.由此可以得出随着污底高度增加，翼型表面阻力显著增加.

图18 不同污底高度下翼型的湍动能分布

由图19可以看出，不同污底密度下湍动能整体分布相似，其阻力特性也相似.但是随着污底密度的增加，流动分离点逐渐向翼型前沿移动，上壁面附近湍动能梯度逐渐减小，下壁面流动分离现象更加显著.

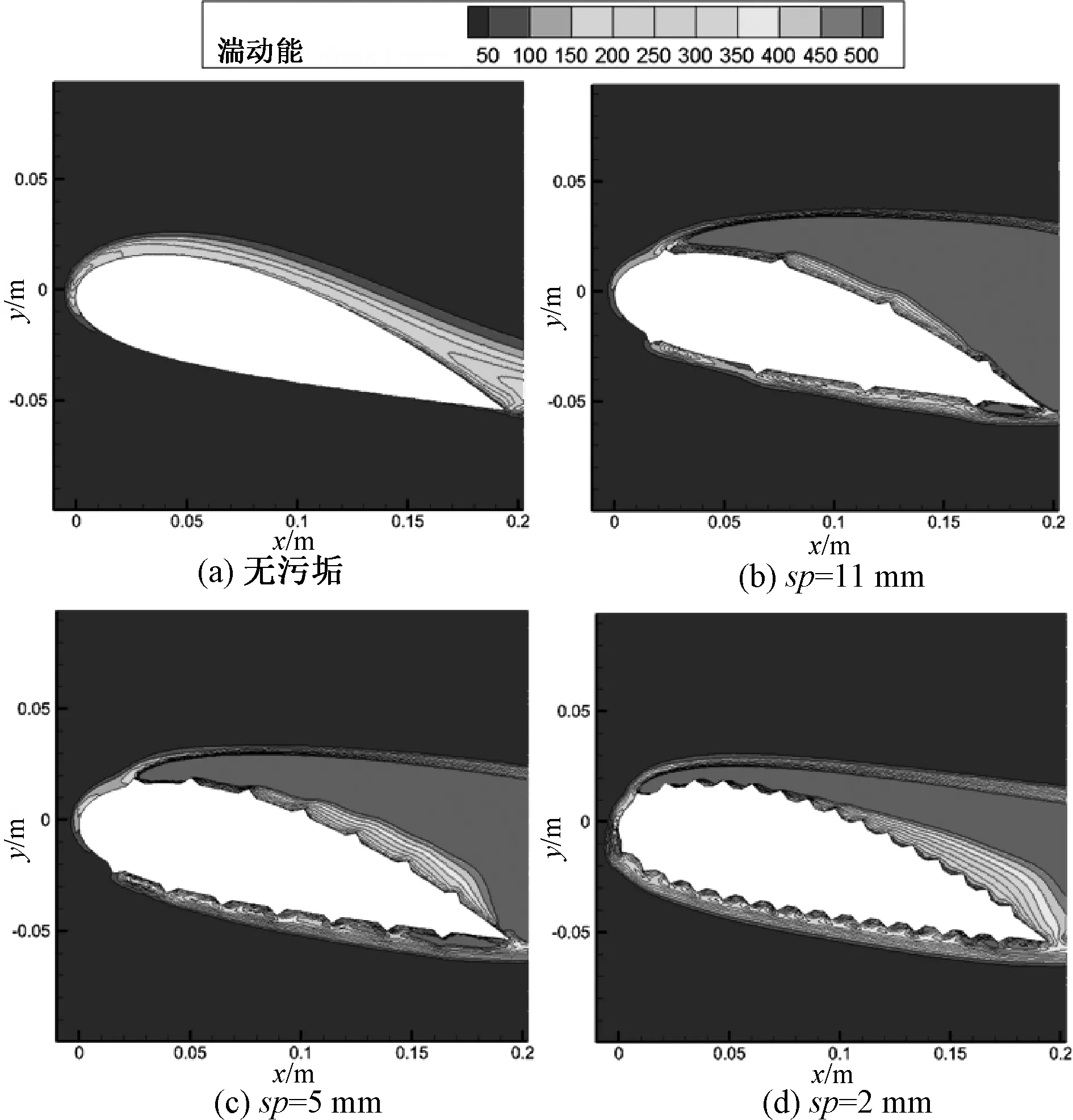
图19 不同污底密度下翼型的湍动能分布

2.3 防污涂层阻力特性分析

针对翼型选取了5个不同迎角α，分别为-5°、0、10°、20°、30°，在这些迎角下分别对表4给出的3种防污涂层进行模拟，将得出的结果与光滑条件下的结果进行比较，如图20.

图20 不同迎角α下3种涂层及光滑条件下翼型升阻比

由图20可得，随着迎角的增大，翼型在10°左右翼型升阻比存在最大值.这是由于当迎角较小时，随着迎角的增大，在翼型表面上流动分离点向翼型头部移动，其阻力减小，相应的升阻比增大；当迎角达到临界值时，随着迎角继续的增大，流动分离现象已充分发展，此时阻力变化较小，但是翼型升力减小，总体上导致升阻比减小.其次，在覆有涂层情况下翼型的升阻比低于光滑情况下的翼型的升阻比.其主要原因是涂层本身带有一定的粗糙度，而且不同涂层的粗糙度也不尽相同.由图中可以发现，三丁基锡涂层的粗糙度最大，其次是自抛光共聚物涂层和硅酮涂层.

针对潜艇模型选取3种不同速度进行模拟，其分别为3.051、6.096、9.152 m/s.最终得出不同涂层工况下的潜艇阻力系数如图21.可以发现，由于防污涂层的存在使潜艇具有一定的初始粗糙度，导致阻力增加；而三丁基锡的粗糙度最大，导致阻力增加最为显著；对于三种涂层，随着潜艇周围流体速度v的增加，涂层的增阻效果均越明显.将上述结果与文献[15]进行对比分析，发现其反映的趋势基本一致，表明采用sand-grain粗糙度函数预测防污涂层的增阻效果是可行的.

针对两种典型模型的防污预测结果进行对比分析，发现防污涂层的存在对两种模型都有一定的增阻效果，且其增阻原因均为防污涂层本身带有的粗糙度引起的阻力增加；3种涂层中三丁基锡涂层增阻效果最显著，其次是自抛光共聚物涂层和硅酮涂层.因此，对防污涂层在两种模型上的应用可得出相同的结论，防污涂层的存在虽然可以有效预防污底的附着，但是其本身也会增加船体表面粗糙度进而增加阻力，在使用防污涂层时必须同时考虑这两点.

3 结论

(1) 针对NACA-24424翼型的计算结果表明：污底的存在使翼型升阻比最大降低多达80%.随着污底粗糙高度和粗糙密度的增加，翼型升力减小且阻力增大；随着攻角的增大，翼型升阻比先增大后减小，在攻角10°左右存在一个临界值，这是由于随攻角增大流动分离点向翼型前缘移动.同时由于流动分离在翼型表面附近产生低速、高压、高湍动能区，导致翼型阻力显著增加.

(2)由两种模型的防污计算结果可以发现：对于文中给出的3种涂层，其本身的粗糙度最大可使阻力增大20%左右，且每种涂层增阻效果差异明显；相较于硅酮和自抛光共聚物涂层，三丁基锡涂层具有最显著的增阻效果.在3种计算水流速度下，3种涂层增阻效果均随水流速度增大而更显著，但水流速度对阻力效应的影响要弱于涂层种类的影响.因此船舶航行过程中对于涂层的选取不仅需要考虑成本和污染等因素，还需要对涂层的阻力效应进行评估.