城市街道视域景观指数与邻里尺度特征效应

包瑞清 （厄瓜多尔）亚历克西斯·阿里亚斯·贝当古

在公共领域，没有什么元素比街道更重要，这是工作、购物、外出就餐和从事日常活动的活跃场所，也是步行锻炼的主要场所[1]。居民更有可能在具有吸引力的街道散步休闲，这有助于身心健康，而负面的视觉因素和街道空间结构则阻碍居民参与到街区的体能活动中[2-3]。

城市街道空间的景观质量提升、量化管理和城市微更新往往需要宏观把握城市开放空间特征分布，进而确定规划区域、内容和时序。目前对城市街道的研究涉及多个方面，依据相关研究方向，可分为身心健康[4-6]、体能活动[3,7-10]、健康福祉[11-14]、感知安全[15-16]、视听质量[17-18]、热舒适性[19]、交通安全[20]、经济与种族[21-22]、街道犯罪[23]、可获取的街道绿化与量化[6,24-25]，及视觉图像与实际调查审计比较[26]和在线审计的可靠性[27]等。虽然其中Tang等结合图像语义分割对北京历史街区（胡同）进行物理和感知的视觉质量评价[17]，但在城市宏观尺度下，基于视域景观指数探索城市街道微观尺度特征分布，尤其是邻里尺度效应等内容鲜见。相较由平面类数据计算景观指数，城市街道视域景观往往从地面人视点观察空间组成、结构和特征，因此传统宏观调研的遥感影像、局部无人机航拍结合实地调查分析的方法则不完全适合。而海量的街道全景图则使反映城市街道微观尺度景观特征的城市宏观尺度分析成为可能。因此本研究提出城市街道视域景观指数与邻里尺度特征效应，这部分研究的核心包括3部分内容：1）视域景观指数删选，以及新指数的提出与计算；2）城市街道视域景观特征提取和分布，以及视域景观指数对特征分布的贡献度和特征重要指数组成；3）邻里尺度特征效应及影响，包括比较层次聚类时不同邻元数聚类结果变化特征，并以绿视率单指数聚类和15 min步行生活圈多指数聚类下特征信息熵空间分布变化，说明邻里尺度效应的影响。

确定研究的核心问题和研究内容后，在具体分析过程中尝试改进已有的景观指数计算精度。1）在通过视域景观指数提取城市街道特征时，虽然已有研究，例如Ye等通过街景4个方向的图像语义分割来尝试改进视域下绿视率计算方法和精度[24]，但是并未根据不同景观指数选择不同全景数据类型来进一步提升计算的精度，因此本研究提出根据全景图不同数据类型，对应提取视域景观指数的方法。2）提出新的视域景观指数，依据计算机视觉尺度不变特征转换（scale-invariant feature transform, SIFT）提出关键点邻域尺度区间频数，优化城市街道视域景观特征的提取。SIFT可以在影像空间尺度中寻找局部性特征，这里的邻域尺度为可以表征空间不同尺寸对象各像素单元（关键点）的计算半径。

1 研究区域与数据预处理

1.1 研究区域

西安市是中国陕西省省会、特大城市、关中平原城市群核心城市、中国西部地区重要的中心城市。西安市常住人口约1 020.35万人，是公认的十三朝古都，是联合国教科文组织于1981年确定的世界历史名城。选取西安市（34°15′N，108°56′E）碑林区、莲湖区、雁塔区、新城区、未央区和灞桥区6个行政区域作为研究对象，探索基于全景图的城市街道视域景观指数与邻里尺度特征效应及影响。

1.2 数据来源及预处理

1.2.1 数据分析工具

所有计算均由Python编程语言完成（使用Anaconda平台下的Spyder解释器），代码托管于GitHub平台代码仓库。地图则由QGIS软件建立。

1.2.2 数据来源

本研究基于区域尺度进行街道空间组成分析。首先，以西安6个行政区域界定研究范围，提取百度道路数据；道路数据来源于中国专业IT社区CSDN（Chinese Software Developer Network）的开放数据。其次，沿道路每200 m设置一个采样点，共获取14 973个采样点。最后，从百度地图应用下载对应采样点的全景静态图，去掉没有数据的无效采样点1 614个，实际下载的有效全景静态图数为13 359张。

1.2.3 数据预处理

从百度地图应用下载的全景静态图是等量矩形投影图（图1-1）。因此，本研究采用全景图像语义分割方法PASS（panoramic annularsemantic segmentation）深度学习模型[28]，对等量矩形投影图进行像素级语义分割（pixel-wise semantic segmentation，图1-2）。语义分割对象有27类，主要包括建筑、道路、植被、天空、车辆、设施、行人等。在城市街道空间的组成结构分析过程中，需要根据不同的分析内容对数据进行预处理，使其满足分析的要求，改善计算的准确性。极坐标格式全景图（小行星视角360°全景，图1-3、1-4），用于天空相关指数的计算，避免等量矩形投影图受未闭合的天空形状影响。等量矩形投影图和极坐标格式全景图因为投影变形，对象像素所占比例不能最大限度地反映实际视觉下对象比例关系；而立方体格式全景图[29]由前、后、左、右、上、下6张透视图组成（图1-5、1-6），用于语义分割对象占所有像素百分比的统计相对合理。

图1 全景图预处理数据类型Type of preprocessing data in the panoramic static image

2 分析与结果

2.1 视域景观指数筛选及计算

2.1.1 视域景观指数筛选

单个视域景观指数可以反映该指数所体现的景观学意义下城市街道特征，而代表不同景观学意义的所有指数共同作用下的城市特征则是所有特征的组成体现。因此视域景观指数筛选时，在应用全景静态图数据这一条件下，尽量区分各个指数所体现出来的景观学意义，基于此本研究筛选出9个视域景观指数（表1）。

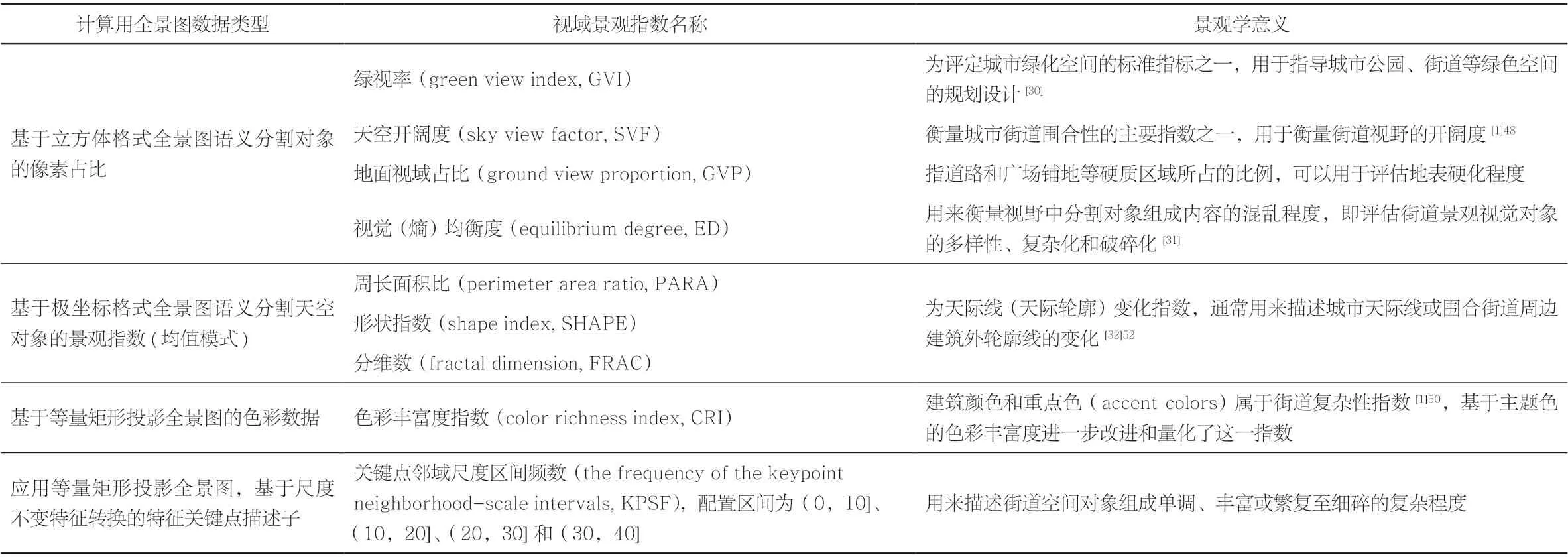
表1 城市街道视域景观指数Tab. 1 Urban street view landscape indices

2.1.2 视域景观指数计算

KPSF为基于计算机视觉尺度不变特征转换提出的新视域景观指数，如果有关键点邻域尺度区间集合为

式中SKP为可探测到的所有关键点邻域尺度，xk为各个关键点邻域尺度大小，位于区间（i，j]；则集合K的基数fKPS表示为

式中fKPS即为KPSF。

计算KPSF，并将结果按照关键点邻域大 小 划 分 为（0，10]、（10，20]、（20，30]和（30，40]4个区间，描述为小尺度、中尺度、较大尺度和大尺度。计算结果显示，当图像内的对象为窗户的角点、招牌的边缘等实际当中较为细碎的对象时，所提取的边缘特征的邻域尺度较小；当对象为天空、成片的墙面等时，所提取的边缘特征的邻域尺度则较大。因此SIFT关键点邻域尺度大小一定程度上反映了街道视域空间繁复的程度。如果图像关键点某一区间的邻域尺度频数接近，则这些图像在该区间具有相似繁复程度的空间对象。基于SIFT算法计算图像各关键点邻域尺度区间频数（图2），结果为：图2-1区间（0，10]为581，（10，20]为155，（20，30]为55，（30，40]为32；图2-2区 间（0，10]为97，（10，20]为23，（20，30]为36，（30，40]为20。为在图中可视化频数分布，将位于区间（0，10]的关键点标识为蓝色空圈；而不在该区间的所有关键点标识为红色圆点，圆点大小表明了关键点的大小。从结果来看，图2-1的（0，10]区间频数最大，次之为（10，20]，说明街道视域空间对象较为细小且繁复程度高，这与图2-2形成鲜明对照，因此说明基于SIFT算法提出的新视域景观指数能够表征街道视域对象的特征。

图2 不同视景关键点邻域尺度区间频数比较Comparison between the frequencies of keypoint neighborhood-scale intervals in different views

2.2 城市街道视域景观特征与邻里尺度的特征效应

计算流程分为4部分。1）选择视域景观指数，包括GVI、SVF、GVP、ED、PARA、SHAPE、FRAC、CRI和KPSF，其中KPSF包 括 区 间（0，10]、（10，20]、（20，30]和（30，40]。2）确定以邻元数为空间尺度配置模式，即各个采样点相邻采样点的个数。配置区间为20个连续序列的邻元数：5～50 m，每5 m一个间隔；50～150 m，每10 m一个间隔。该参数由层次聚类AgglomerativeClustering方法①的输入参数connectivity（连接矩阵）控制，并由kneighbors_graph方法②输入邻元数计算。3）计算各个邻里尺度层次聚类最优簇数，由KElbowVisualizer方法③计算，即计算每个点到其所属聚类中心的平方距离之和，曲线拐点④即为最优的簇数选择。聚类将所有采样点按视域景观指数划分为多个簇（组），每簇内的采样点由视域景观指数赋予相似的特征，增加簇间而缩小簇内的特征异质性，就是寻找最优簇数的过程；4）由最优簇数聚类指数获得各邻里尺度特征分布，并计算指数（特征）贡献度，由SelectKBest方法⑤的方差分析法（analysis of variance, ANOVA）为指数打分计算（配置参数为f_classif），反映聚类簇标签与特征之间线性依赖程度，较高的分值表明该指数对聚类结果有较大影响，为所选指数中对城市街道视域景观特征分布有主要影响的因子。

2.2.1 不同邻里尺度最优簇数

从最终计算结果（图3）可以观察到，20个连续邻里尺度的最优簇数集中于4，其次为5，只有当邻元数为15时，簇数为3。同时可以观察到，当邻元数增加，邻里尺度增大时，不同邻里尺度聚类的测量分值（配置参数为distortion，即计算从每个点到其指定中心的平方距离之和）拉开的距离开始减小。这表明视域景观指数随邻里尺度的增加，在相同簇数下，较高的邻元数趋向于较低的分值，表现为簇间的异质性相对不明显，簇内的异质性有所增加，对特征集聚的效应有所减弱。

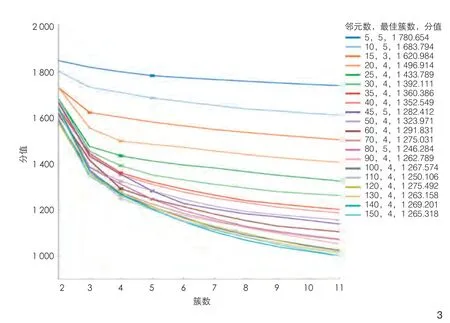
图3 最优簇数选择Optimal cluster number selection

2.2.2 不同邻里尺度景观指数贡献度

从最终计算结果（图4）可以观察到：不同邻里尺度下GVI对聚类特征的贡献度基本占绝对优势；其次为KPSF（10，20]、KPSF（0，10]和SVF；再者为CRI、KPSF（20，30]、PARA、KPSF（30，40]；对聚类特征贡献度最小的是ED、GVP、SHAPE、FRAC。其中当邻元数小于40时，GVI和SVF占主导；邻元数大于等 于40时，主 要 以GVI和KPSF（10，20]、KPSF（0，10]占主导。

图4 指数贡献度Metrics contribution

贡献度的分值变化同最优簇数选择分值变化均具有邻里尺度效应。随邻里尺度的增加而增加，但当到达一定尺度后，变化趋于平缓，同样表明视域景观指数随邻里尺度的增加，对特征集聚的效应开始相对减弱。

2.2.3 不同邻里尺度的特征聚类

在邻元数不大于15时，分析所在采样点所考虑的邻近采样点数量较少，邻近采样点往往具有相似的特征组成和结构，并以GVI和SVF为聚类特征主导。因次，从聚类结果（图5）可以得知，当邻元数较小时聚类结果具有明显连续成片的分区特征。例如当邻元数为5时，可以明显区分为西北区域、二环到绕城区间、老城（中心城区）和雁塔区、汉长安城未央宫区域，及灞桥区纺织城区域。当邻里尺度增加，KPSF（10，20]、KPSF（0，10]对特征聚类的影响开始增加，并超过SVF，分析所在采样点所考虑的邻近采样点数量较多，采样点之间的特征组成和结构变化增多，原来具有较大连续性集聚的特征分区，开始分解为较多分散的、小的集聚分区。对于特征的表述也从较小邻元数的局部性特征向较大邻元数的区域性特征转变。

图5 聚类结果示例Examples of clustering results

3 讨论

3.1 基于全景图不同数据格式计算城市街道视域景观指数

Ye等在测量街道空间绿视率时，抓取谷歌街景水平视点4个方向上的图像作为图像分割数据[24]；Tang等下载腾讯地图街景图像做图像分割，计算对象比例[17]。而使用全景图的不同数据类型分别用于不同类型指数的计算，可以进一步提升指数计算的精度：将等量矩形投影图用于色彩丰富度指数、关键点邻域尺度区间频数的计算；极坐标格式全景图用于天际线变化指数的计算；立方体格式全景图用于街道空间对象视域占比指数测量。

3.2 关键点邻域尺度区间频数应用的可行性

图像匹配是应用计算机视觉解决许多问题的一项基本研究，包括对象和场景识别、多个图像中寻找三维结构和运动追踪等。Lowe提出的尺度不变特征转换，可以不受图像变形、噪声等影响，有效提取图像的特征[33]。为进一步提取城市街道空间不同属性的特征，依据尺度不变特征转换关键点描述子定义关键点邻域尺度区间频数指数。所有街道特征指数聚类贡献度结果进一步证明了关键点邻域尺度可以作为城市街道空间重要特征之一，通过确定相应关键点邻域尺度区间频数大小，能够有效识别不同特征的城市街道区域。

3.3 视域景观指数受不同邻里尺度的特征效应影响和应用示例

大量研究证实，地理学研究对象格局与过程的发生、时空分布、相互耦合等特性都是尺度依存的（scale-dependent）[34]，例如韩贵锋等在地表温度与植被指数相关性的空间尺度特征研究上，选取了30～8 000 m之间变化间隔的9个空间尺度[35]。但是受到数据可获取性、数据分析方法和技术要求等各类因素的限制，对于涉及尺度相关的研究问题或采取定性分析，或选取一个到多个非连续的部分尺度进行数据分析。

在空间尺度配置的对象上，可初步分为2种情况：通常情况是对研究范围精细度的划分，例如以30或60 m单元格划分研究范围，每一单元格为最小研究对象[35]；再者是分析对象各个空间点的缓冲距离或者邻元数。不同空间尺度配置方式会对结果造成影响，例如空间异质性基于前者通常随尺度增大而降低；而基于后者，通常随尺度增大而增大。

3.3.1 通过不同空间尺度聚类区划研究对象

在研究城市街道绿化时，通过绿视率量化的常规区间分区（图6-1）不能很好分区实现精细化管理，但可以通过聚类的方法尽量将绿视率接近的位置归为一个区域，便于宏观统筹（图6-2～6-4）。从箱型图（图7）观察10-5（邻元数-最优簇数）聚类结果的分离性，除簇1和簇4之外，分离性均较好。虽簇1和簇4具有类似的聚类特征，但是2个簇类分别位于不同的区域，表明这2个不同区域具有类似的绿视率指数特征。同时比较了邻元数与最优簇数为25-4和140-4的绿视率指数单独聚类结果，表明如果考虑的邻元数增多，尺度增加，则区域细化程度升高，即空间异质性增加。

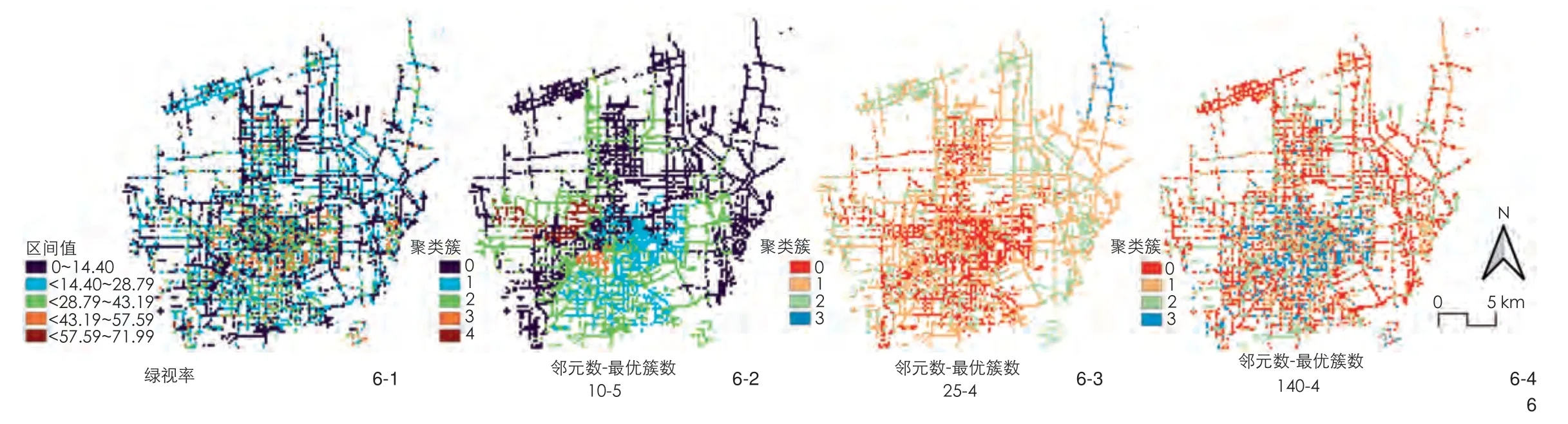
图6 绿视率及不同尺度下的聚类Green view index and clustering at different scales

图7 绿视率指数值聚类分布Clustering distribution of green view index values

3.3.2 不同空间尺度15 min步行生活圈的熵值变化

计算多指数聚类特征15 min步行生活圈（半径约1 100 m）的熵值结果（图8），分析邻元数分别为5、10和30下的多指数聚类特征信息熵分布。从结果来看，随空间尺度的增加，信息熵整体增加，即空间异质性增加。统计所有采样点各个邻里尺度下信息熵值分布与特征簇类数量的关系，其结果为：当簇类数为2时，信息熵值域为[0.027，0.693]；为3时，值域为[0.112，1.099]；为4时，值域为[0.336，1.386]；为5时，值域为[0.778，1.607]。由此可见虽然各特征簇类数量的信息熵值域是相互交错的，但从基本趋势可以判断较高的信息熵相对具有较多特征簇类，反之具有较少特征簇类。多指数聚类特征信息熵的高低一定程度上反映了城市活力的高低或城市风貌多样（混杂）程度，对城市空间序列、风貌景观组织优化、城市视觉等区域控制具有参考价值。

图8 15 min步行生活圈多指数聚类特征信息熵Information entropy of multi-index clustering features within the 15-minute-walking living circle

同时，单独提取了城市中的5个位置点，分别为西安建筑科技大学西门、钟楼、大明宫南门、西安北站和曲江立交。观察各个位置点信息熵随邻元数变化趋势（图9），结果表明：西安建筑科技大学西门、钟楼、大明宫南门均位于二环以内较为繁华区域，较之位于偏远区域的西安北站和曲江立交具有更高的信息熵；可以观察到各位置点均表现出尺度依存的特征，信息熵随邻元数增加而逐渐增加，当邻元数约为30～50时趋于平稳。因此在平稳状态下分析比较不同位置点视域景观指数聚类信息熵，可以较为准确地观察城市街道视域景观丰富程度的变化特征。

图9 位置点信息熵变化曲线Information entropy change curve of location points

3.4 局限性

PASS全景图语义分割的均交并比（mean intersection-over-union, mIoU）约为54.3%，全景图的分辨率为1 024×512 px，同时用于拍摄全景图的车辆占据了地面较大的空间，均会在一定程度上影响图像语义分割和特征指数计算结果的精度。区域尺度全景图是沿道路每200 m设置一个采样点，较大距离的采样点对区域尺度的特征指数聚类和特征的具体分布有一定程度影响。上述对分析结果精度有影响的因素无法完全避免，但是未来可以尝试增加密集的采样点，并通过算法的改进和方法的调整使精度进一步提升。

同时，百度地图全景静态图各个节点拍摄时间存在差异，也并未提供具有时间序列的历史图像，限制了城市街道特征时间轴向的分析。

4 结语

本研究以全景静态图数据为分析的基础，通过当前计算机视觉发展的相关算法，解析反映城市街道的图像内容，包括语义分割、尺度不变特征转换来计算绿视率、天空开阔度、地面视域占比、视觉（熵）均衡度、色彩丰富度指数，及天空形状的周长面积比、形状指数和分维数，并提出关键点邻域尺度区间频数等指数。应用能够反映城市街道特征的视域景观指数，由层次聚类连接矩阵的邻元数变化作为空间尺度配置方式，探索不同邻里尺度下视域景观指数聚类后的特征空间分布变化及指数贡献度；并列举空间尺度变化下，基于单指数绿视率的特征区域提取和多指数聚类信息熵的特征分布变化，表明对城市街道视域景观指数和邻里尺度特征效应的分析，可以为城市街道空间的景观质量提升、量化管理和城市微更新提供参照。

基于城市街道视域景观指数分析城市街道特征分布是对城市街道建成环境的一种评价途径，在进一步的研究中，可以结合百度地图应用中的兴趣点（point of interest,POI）数据，由协方差逆矩阵和AP聚类算法（affinity propagation, AP）计算分析行业分类服务的业态空间分布结构，或计算POI密度曲线，以自然断点法分类识别城市活力中心[36]。通过耦合建成环境街道特征分布和反映城市生活的业态空间分布及活力分布，能够提取综合的城市街道特征空间模式，权衡建成环境和生活服务的匹配关系。

致谢(Acknowledgments)：

该论文的完成是基于伊利诺伊理工大学（IIT）无人驾驶城市项目，非常感谢项目组中城市景观组的Ronald Henderson、Nilay Mistry，以及工程组的Matthew Spenko、Boris Pervan、陈舣合（Yihe Chen）、Kana Nagai。

注释(Notes)：

① 为机器学习库scikit-learn提供的层次聚类模型AgglomerativeClustering（scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.html）。

② 为机器学习库scikit-learn提供的邻元加权图kneighbors_graph（scikit-learn.org/stable/modules/generated/sklearn.neighbors.kneighbors_graph.html）。

③ 为python库Yellowbrick提供的最优簇数选择工具KElbowVisualizer（www.scikit-yb.org/en/latest/api/cluster/elbow.html）。

④ 即斜率（求导）的变化最大值，使用Elbow方法（www.scikit-yb.org/en/latest/api/cluster/elbow.html）。

⑤ 为机器学习库scikit-learn提供的特征选择工具SelectKBest（scikit-learn.org/stable/modules/generated/sklearn.feature_selection.SelectKBest.html）。

图表来源(Sources of Figures and Table)：

文中图表均由作者绘制，其中图1-1、1-3、1-5、2全景静态图下载自百度地图（2021年4月）。