考虑注浆圈与复合衬砌时体外排水方式设计

傅鹤林，安鹏涛†，成国文，王仁健，李鲒，余小辉

（1.中南大学土木工程学院，湖南长沙 410075；2.高速铁路建造技术国家工程实验室（中南大学），湖南长沙 410075；3.广东省南粤交通投资建设有限公司，广东广州 510101）

“以堵为主、防排结合”的控制型防排水原则是目前富水区隧道涌水处置的首选准则[1-6].但运营情况表明[7-11]，排水堵塞时因衬砌水压力过高引发的仰拱开裂、轨道隆起、隧底翻浆冒泥等底部结构病害问题时有发生，针对上述工程问题，合理选择隧道防排水方式是有效解决措施之一[12]，其中文献[13]提出了一种排导能力强、隧底降压效果优的体外排水方式，此种排水方式在隧道正下方设置排水洞，将隧道支护结构外的渗水直接渗流至排水洞，降低了隧道拱底的渗水压力.

依托地下水经环、纵向排水管与横向排水管流入侧沟，再由侧沟与中心水沟共同排出隧道的常规排水方式，文献[14-22]针对注浆圈的参数设计及涌水量计算问题进行了深入研究，分析了注浆圈的堵水作用机制，为注浆圈的设计提供了理论基础.针对体外排水方式，文献[23-24]利用数值分析软件对渗流场与衬砌水压力分布规律进行了探讨；文献[25-26]以镜像法和渗流力学理论为基础，推导了半无限平面内深埋式中心水沟排水时隧道渗流场及涌水量的解析解.

综上所述，国内外学者对常规排水方式下隧道涌水量及渗流场的分析较为广泛，而对体外排水方式下隧道及体外排水洞涌水量的理论分析较少，同时考虑注浆圈与复合衬砌时更鲜有涉及，但现有研究方法与思路仍值得借鉴.为此，构建是否含注浆圈的两种体外排水简化计算模型，以反映法、叠加原理及渗流力学理论为基础推导隧道与体外排水洞涌水量的计算公式、隧道二次衬砌外水压力表达式，并进行退化验证，同时对特征参数进行敏感性分析，并通过数值模拟进行验证，以求对体外排水方式下注浆圈及支护结构的设计进行有意义的尝试与补充.

1 无注浆时渗流场解析解

1.1 计算模型及基本假定

建立半无限平面内隧道与体外排水洞渗流模型，如图1所示.

图1 不含注浆圈时隧道与体外排水洞渗流模型Fig.1 Seepage model of tunnel and external drainage tunnel without grouting ring

图1 中，r0、re、rc分别为二次衬砌内径、二次衬砌外径及初期支护外径；体外排水洞半径为rd；体外排水洞与隧道初期支护外径最小距离为h0；隧道圆心至给水边界竖直距离为d；地下水水位为H.

考虑实际工况及方便问题解答，作如下假定：

1）围岩与各结构均质且各向同性；

2）隧道与体外排水洞均处于稳定渗流状态；

3）渗流服从达西定律；

4）隧道为大埋深.

1.2 模型求解

利用反映法，将半无限双孔隧洞渗流场转化为无限渗流场下4个单孔隧洞的叠加问题，如图2所示.

图2 不含注浆圈时隧道与体外排水洞渗流模型镜像图Fig.2 Mirror image of seepage model of tunnel and external drainage tunnel without grouting ring

点M（x，y）为渗流场中任意点；R1、R2、R3、R4分别为点M至各孔洞中心点的距离；Q1与Q2分别为体外排水洞与隧道涌水量.

根据假定，水流速度与水力坡度满足达西定律，表达式为：

式中：v为渗流速度；k为介质渗透系数；i为水力坡度.

根据渗流力学原理，无限平面内单孔隧洞稳定径向渗流连续性方程极坐标表达式为：

式中：ρ为计算点至孔洞中心的距离；Φ为无限平面内计算点的渗流场水头势函数.

假定某断面的流量为Q，则：

对式（3）积分得：

式中：c为待定常数，其值由边界条件确定.

当无限平面内4 个孔洞均达到稳定渗流时，平面内任意一点水头势函数根据势的叠加原理确定，计算式为：

式中：Qi为第i个孔洞的涌水量；c1为待定常数.

假定围岩渗透系数为kr，当M点位于围岩范围，则水头势函数表达式为：

由给水边界条件y=0时，Φ=H可知：

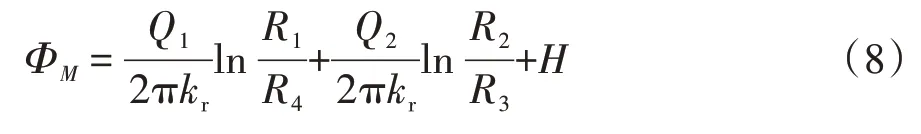
由于假定为深埋，忽略隧道复合衬砌外缘各位置渗流的离散型，对隧道结构有：

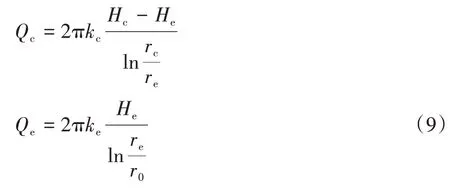
式中：Qc、Qe分别为实际隧道中初期支护外缘、初期支护内缘涌水量；Hc、He分别为实际隧道初期支护外缘、初期支护内缘的水头高度；kc、ke分别为初期支护及二次衬砌的渗透系数.

据流体质量守恒定律

以隧道轴线位置为参考面，对实际隧道初期支护外缘及体外排水洞边缘有：

联立式（9）～（12），得：

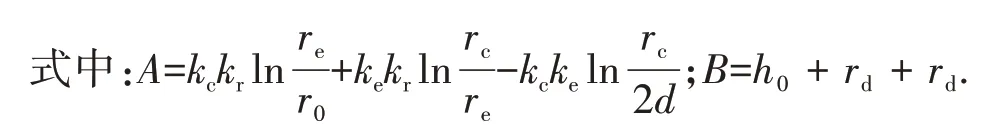
1.3 解析结果验证

1）h0无穷大

若体外排水洞与隧道初期支护外径最小距离h0趋于无穷大，则有

此时式（13）退化为半无限平面内无支护隧道的最大涌水量计算公式；式（14）退化为半无限平面内设置复合衬砌时隧道的涌水量计算公式［27］.

2）rd无穷小

若体外排水洞洞径rd无穷小，则有：

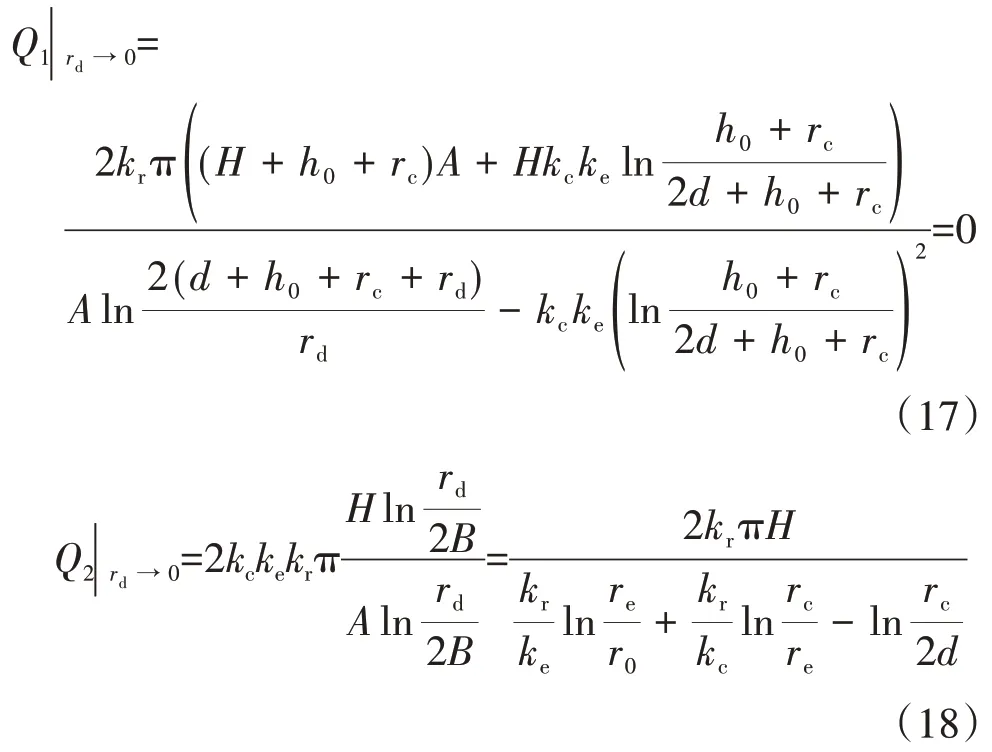
此时式（13）趋近于0，与事实符合；式（14）退化为半无限平面内设置复合衬砌时隧道的涌水量计算公式.

由式（15）～（18）可知，式（13）（14）均可退化为半无限平面内单孔孔洞涌水量计算公式，而半无限平面内单孔孔洞涌水量计算公式为本文所得体外排水洞稳定渗流的特例，验证了本文计算公式的正确性.

联立式（9）（10）与（14），计算隧道二次衬砌外水压力表达式为：

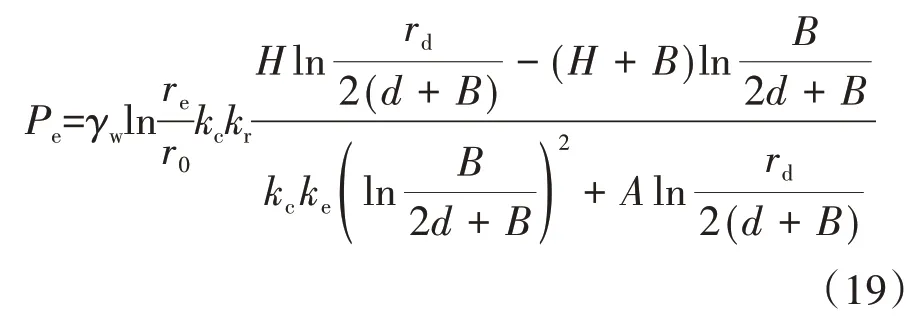
式中：γw为水的重度.

2 含注浆圈时渗流场解析解

2.1 计算模型及基本假定

建立半无限平面内含注浆圈时隧道与体外排水洞渗流模型，如图3所示.

图3 含注浆圈时隧道与体外排水洞渗流模型Fig.3 Seepage model of tunnel and external drainage tunnel with grouting ring

图3中，rg为注浆圈外缘半径，其余参数同图1.

2.2 模型求解

由式（8）可知，注浆圈外缘界面水头势函数为：

此时对隧道与体外排水洞而言，注浆圈外缘为定水头边界.由式（5）可知，注浆圈内任一点水头势函数表达式为：

式中：Φ*表示注浆圈区域内任一点的水头势函数；kg为注浆圈渗透系数；c2为待定常数.

由式（21），依次计算注浆圈外缘、隧道初期支护外缘及体外排水洞洞壁水头势函数：

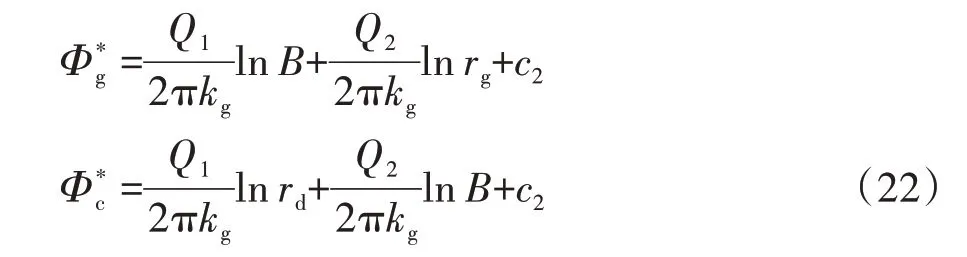
流入初期支护与二次衬砌的渗水量满足流体质量守恒定律.由式（9）可得：

联立式（20）与式（22）（23），得：

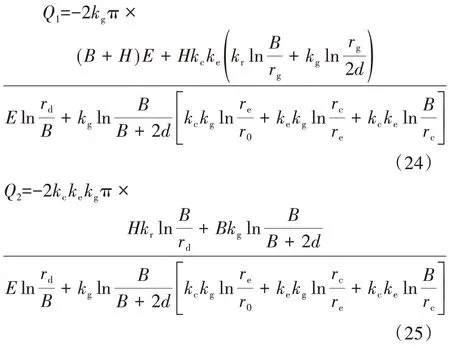
式（24）（25）中：

2.3 解析结果验证

若未施加帷幕注浆，可令kr=kg，式（24）与（25）退化为：

忽略注浆圈外缘水头高度的离散型，式（27）（28）可分别退化为式（13）（14），而注浆圈外缘水头高度在非富水区时随注浆圈外缘的位置而变化，因此式（27）（28）仅适用于给水边界距隧道轴线位置较大的工况，此时B+2d≈2d，则式（27）退化为（13），式（28）退化为（14）.即仅含复合衬砌支护结构为本节所推导的含注浆圈及复合衬砌支护结构的计算特例，验证了本节计算公式的正确性.

联立式（9）（25）（26），可计算隧道二次衬砌外水压力.

3 特征参数敏感性分析

鉴于所推导体外排水洞及隧道涌水量与二次衬砌外水压力计算公式影响参数众多，直接分析较为复杂.现对体外排水方式的主要特征参数进行探讨分析.

3.1 注浆圈渗透系数

假定给水边界H=200 m；注浆圈厚度为6 m；隧道尺寸参数r0、re、rc分别为：6 m、6.5 m、6.8 m；原岩渗透系数为2×10-6m/s，注浆圈与初期支护及二次衬砌渗透系数的比值分别为200、100.涌水量及隧道二次衬砌外水压力随注浆圈渗透系数的变化关系分别如图4与5所示.

图4 涌水量随注浆圈渗透系数的变化曲线Fig.4 Variation curve of water inflow with permeability coefficient of grouting circle

图4 与图5 表明体外排水洞与隧道涌水量均随注浆圈渗透系数的下降而非线性降低；隧道二次衬砌外水压力随注浆圈渗透系数的下降而非线性增大.其中原岩与注浆圈渗透系数比值（kr/kg）小于15时，注浆圈渗透系数对涌水量及隧道二次衬砌外水压力敏感性显著；当原岩与注浆圈渗透系数比值大于15 时，继续降低注浆圈渗透系数对体外排水洞与隧道涌水量及二次衬砌外水压力影响均较弱.解析结果与文献［10］的研究结果具有一致性.

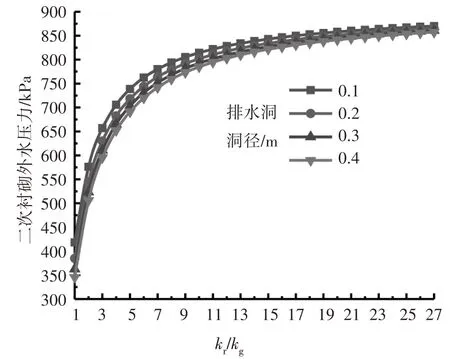
图5 二次衬砌外渗水压力随注浆圈渗透系数的变化曲线Fig.5 Variation curve of external seepage pressure of secondary lining with permeability coefficient of grouting circle

综合考虑经济及排水因素，注浆圈渗透系数与原岩合理比值为15，而未实施体外排水洞时原岩与注浆圈渗透系数合理比值建议在两个数量级内［28-30］，表明设置体外排水洞时帷幕注浆在较高渗透系数时同样可发挥明显作用.原因为：未设置体外排水洞时，涌水通过隧道二次衬砌背后的环向盲管、纵向与横向排水管，进而利用水沟排出隧道，此时注浆圈内的涌水需经较长渗流路径才可排出隧道，而设置体外排水洞时注浆圈内的渗水可直接排出，渗流路径缩短，故对注浆圈堵水功能降低了要求，此时可减小注浆量，以达到安全、经济的最优效果.

同时随排水洞洞径增大体外排水洞涌水量增加而隧道涌水量及隧道二次衬砌外水压力降低，但排水洞洞径对排水洞涌水量的影响更为显著.如kr/kg为3，体外排水洞洞径为0.1 m、0.2 m、0.3 m 及0.4 m时，排水洞涌水量（m3·d-1·m-1）为：12.41、14.18、15.45、16.51，分别增加：14.23%、24.54%与32.99%；隧道涌水量（m3·d-1·m-1）为2.97、2.85、2.76、2.69，分别降低：4.1%、7.02%与9.38%；隧道二次衬砌外水压力为：656.83、629.89、610.71 及595.21，分别降低4.1%、7.02%与9.38%，表明通过增大排水洞洞径而降低二次衬砌外水压力的同时会增加更多的涌水量，对当地水源破坏会加剧，因此体外排水洞洞径的确定需综合考虑支护结构受力及隧址区环境要求.

3.2 复合衬砌

3.2.1 初期支护

假定体外排水洞洞径为0.2 m，原岩与注浆圈渗透系数比值为15，其它参数同3.1 节，绘制涌水量及外水压力与初期支护的关系如图6所示.

图6 涌水量及外水压力与初期支护的关系Fig.6 The relationship between water inflow and external water pressure with initial support

由图6 可知，随初期支护渗透系数的降低体外排水洞涌水量与隧道二次衬砌外水压力非线性增大，隧道涌水量非线性降低，其中初期支护渗透系数对隧道涌水量、隧道二次衬砌外水压力、体外排水洞涌水量的影响程度逐渐减弱.

同时随初期支护厚度的增加隧道二次衬砌外水压力与隧道涌水量急剧下降，而对体外排水洞涌水量影响较弱.如kg/kc为60，初期支护厚度为0.2 m、0.3 m、0.4 m 及0.5 m 时，排水洞涌水量（cm3·d-1·m-1）为：3.34、3.41、3.47、3.5，分别增加：2.28%、3.87%与5.02%；隧道涌水量（cm3·d-1·m-1）为2.67、2.27、1.98、1.76，分别降低：14.75%、25.56%与33.82%；隧道二次衬砌外水压力（kPa）为：884.49、754.04、658.43 及585.35，分别降低14.75%、25.56%与33.82%，表明可通过增加初期支护的厚度达到降低二次衬砌外水压力及隧道涌水量的目的.

设置体外排水洞时，隧道排水通道畅通，注浆圈内的渗水可快速通过体外排水洞排出，降低了对隧道支护结构的作用，因此初期支护对体外排水洞涌水量影响较弱.

3.2.2 二次衬砌

假定体外排水洞洞径为0.2 m，初期支护厚度0.4 m，原岩与注浆圈、注浆圈与初期支护渗透系数比值分别为15 与100.其余参数同3.1 节，涌水量及外水压力与二次衬砌相关参数的关系如图7所示.

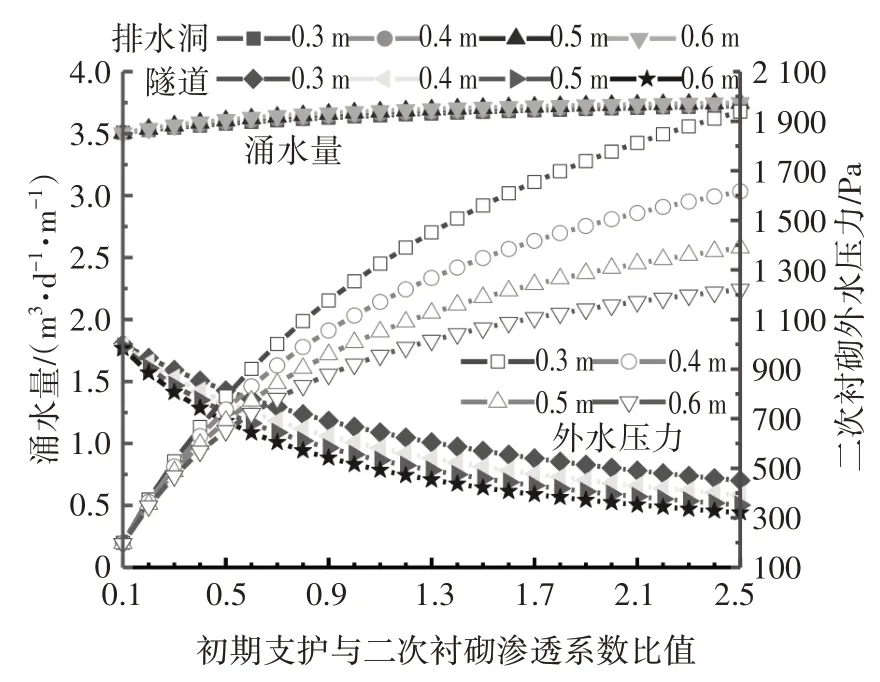
图7 涌水量及外水压力与二次衬砌的关系Fig.7 The relationship between water inflow and external water pressure with secondary lining

由图7 可知，随二次衬砌渗透系数的降低体外排水洞涌水量与隧道二次衬砌外水压力非线性增大，隧道涌水量非线性降低，其中二次衬砌渗透系数对隧道涌水量及隧道二次衬砌外水压力影响程度大于对体外排水洞涌水量的影响程度.

随二次衬砌厚度的增加，隧道涌水量与二次衬砌外水压力均减小，体外排水洞涌水量基本保持不变.当二次衬砌与初期支护渗透系数比值为1.5，二次衬砌厚度为0.3 m、0.4 m、0.5 m 及0.6 m 时，隧道涌水量（m3·d-1·m-1）为：0.94、0.81、0.72 及0.64，涌水量分别降低：13.58%、23.78%及31.71%；隧道二次衬砌外水压力（Pa）分别为：1 560.08、1 348.15、1 189.15及1 065.45，分别降低：13.58%、23.78%及31.71%，表明适当增加二次衬砌厚度可降低二次衬砌外水压力与隧道涌水量.

综合分析，设置体外排水洞时可降低注浆量以保证原岩与注浆圈渗透系数比值维持在较低水平（10～15），注浆圈与初期支护渗透系数比值可保持在100 附近，同时须严格控制二次衬砌渗透系数，在此基础上可通过增加初期支护与二次衬砌的厚度达到降低隧道涌水量与二次衬砌外水压力的目的.同时排水洞洞径对体外排水洞排水量影响显著，为保护当地水源平衡，体外排水洞洞径需控制在合理范围.

4 数值模拟分析

为验证本文构建模型的合理性及公式推导的正确性，以鸿图隧道在建工程为背景进行数值模拟分析.

4.1 工程背景

鸿图隧道位于广东省，左线与右线长分别为6 336 m 与6 337 m，为分离式双向四车道公路隧道，最大埋深约739 m，处于区域性大断裂莲花山断裂带.同时隧道紧邻飞泉电站、飞泉水库、三度水库及下穿黄棉湖水库，部分断层与大型水体相连，突涌水风险极高，如图8所示.

图8 地形地质纵断面图Fig.8 Topographic and geological profile

4.2 参数选取

含仰拱的曲墙式隧道断面，较接近圆形，此时将隧道断面假定为圆形，误差一般在可接受范围［31］.采用等代圆法将非圆形隧道转化为圆形隧道进行研究，文献［32］对等代圆半径进行了分析，本文取隧道断面外接圆半径为等代圆半径，表达式为：

式中：r0表示原隧道做等代圆处理后的半径；b表示原隧道的断面跨度；h表示原隧道的断面高度.

计算得等代圆半径r0=6.2 m.据第3 节分析，体外排水洞洞径为0.2 m，初期支护与二次衬砌厚度分别设计为40 cm 与50 cm，注浆圈厚度为6 m，静水头高度为250 m，结合设计院与现场测试及施工经验，材料参数如表1所示.

表1 材料参数Tab.1 Material parameters

4.3 三维模型建立

采用有限差分软件FLAC3D进行模拟，考虑施工过程中的空间尺寸效应，按照估算与试算结果，确定模型尺寸为：x×y×z=100 m×50 m×100 m，隧道埋深为50 m.原岩、注浆圈、初期支护及二次衬砌均采用实体单元，模型四周为透水边界，底部不透水，约束模型四周法线方向上的位移，模型底部为固定端约束.顶部施加均布力，弥补地应力的不足，材料参数按表1取值.

4.4 结果对比

分别提取隧道二次衬砌外缘（顶部、底部、左边墙、右边墙，并求平均值）渗水压力及涌入体外排水洞与隧道涌水量，结果如表2所示.

表2 结果对比Tab.2 Comparison of results

由表2 可知，理论值与模拟值有一定差异，其中隧道二次衬砌外水压力、隧道涌水量、体外排水洞涌水量分别相差：8.66%、9.46%与11.11%，误差在可控范围内，差异的原因是等代圆近似替代及理论公式推导时忽略隧道支护结构及注浆圈外水压力的离散型.数值模拟进一步验证了本文所推导公式的正确性，也为体外排水方式的设计提供了理论依据.

5 结论

针对是否含注浆圈的两种体外排水简化计算模型，通过反映法、叠加原理及渗流力学理论推导了隧道与体外排水洞涌水量的计算公式、隧道二次衬砌外水压力表达式，并进行了退化分析，最后利用数值模拟手段进一步得到了验证，具体结论为：

1）推导了隧道与体外排水洞涌水量的计算公式、隧道二次衬砌外水压力表达式，未设置注浆圈时计算公式可退化为半无限平面内单孔孔洞涌水量计算公式，设置注浆圈时计算公式适用于给水边界较大的工况；

2）未设置体外排水洞时，涌水通过隧道二次衬砌背后的环向盲管、纵向与横向排水管，进而利用排水沟排出隧道，此时注浆圈内的涌水需经较长渗流路径才可排出隧道；而设置体外排水洞时注浆圈内的渗水可直接排出，渗流路径缩短，故对注浆圈堵水功能降低了要求，此时可减小注浆量，以达到安全、经济的最优效果；

3）注浆圈与初期支护渗透系数合理比值为80～120，同时须严格控制二次衬砌渗透系数，在此基础上可通过增加初期支护与二次衬砌的厚度达到降低隧道涌水量与二次衬砌外水压力的目的；

4）排水洞洞径对体外排水洞排水量影响显著，为保护当地水资源，体外排水洞洞径需取适宜值.