基于卡尔曼滤波原理对长春市温、湿度的网格预报试验
应 爽 刘海峰 于月明 霍 也
(1.长春市气象局,吉林 长春 130012;2.吉林省气象局,吉林 长春 130062)
1 引言
温度和湿度等要素预报是天气预报的重要组成部分。近年来,气象要素预报和服务面临的精细度和准确度需求在不断提升, 制作无缝隙精细化网格预报已成为发展趋势[1,2]。 由于目前的数值天气预报模式在时空分辨率和预报准确度等方面,与上述需求之间仍存在差距, 依靠数值模式制作精细化要素预报, 需要对模式进行降尺度和偏差订正等后处理[3]。
卡尔曼滤波及其改进算法——递减平均法,是数值模式统计后处理的重要方法, 在针对单一模式进行偏差订正、 对多模式进行集成以及对模式进行统计降尺度等方面, 均有广泛应用和令人满意的效果[1,3-7]。 而且,基于卡尔曼滤波原理的订正预报模型对数值模式和季节的变化具有较好的适应性[8]。 近年来,为了减小集合预报的偏差并合理调整离散度,马旭林等[9]在基于递减平均法的一阶矩和二阶矩偏差订正方案基础上, 发展了综合偏差订正方案, 方案对集合平均偏差和离散度均有良好的订正效果。 针对剧烈降温条件下订正效果不理想问题,肖瑶等[10]通过将递减平均参数构建为跟随空间和天气过程变化的函数, 有效降低了预报误差。在精细化预报技术研究方面,赵长健等[11]基于5km×5km 格点数值预报和上海市崇明区24 个自动站观测资料,进行了数值预报偏差订正工作;齐铎等[12]采用递减平均法,对中国东北中北部极端温度数值预报进行了偏差订正, 得到了时间分辨率为3h、空间分辨率为0.05°×0.05°的格点预报;肖瑶等[13]应用递减平均法,对河南省高速公路沿线逐3h 极端气温精细化指导预报产品进行了偏差订正。 利用高精度数值模式预报和格点实况数据,基于卡尔曼滤波原理,进行精细化网格预报的研究尚不多见。
本文利用区域数值模式预报数据、 陆面同化格点数据,以长春市气温(2m 温度)和相对湿度预报为研究对象,采用卡尔曼滤波、递减平均法,进行数值模式格点预报偏差订正建模试验, 探索气温和相对湿度的精细化网格预报方法。
2 数据与方法
2.1 数据及其预处理
本文的研究区域为一个能够包含长春市(2017 年) 范围的矩形, 具体是124°20′46″E—127°07′48″,43°11′68″—45°20′45″。
预报数据采用区域数值模式 (Weather Research and Forecasting,WRF)的2m 温度和相对湿度预报数据, 实况数据采用中国气象局陆面数据同化系统 (CMA Land Data Assimilation System,CLDAS)的气温和相对湿度同化数据,预报和实况数据的时间分辨率均为1h, 空间分辨率分别为3km×3km、5km×5km。建模数据样本的时间范围为2017 年1 月1 日—6 月30 日,时间分辨率是1h,剔除缺失值后,样本为98d。 应用克里金插值法,将实况数据插值为空间分辨率为3km×3km 的数据,预报和插值后实况数据的格点数均为104×81个。 试报样本的时间范围为2019 年8 月1—10日,时间分辨率均为1h。
2.2 建模方法
2.2.1 卡尔曼滤波
卡尔曼滤波(Kalman Filter,KF)[14]是一个最优化自回归数据处理算法, 它利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计, 具有动态建模、 样本数量需求低等优势。 其公式如下:

式中,i 代表时间;xi和yi分别为系统性偏差和预报误差,满足xi=xi-1+wi,yi=xi+vi,wi和vi是均值为0的 随 机 变 量;Wi、Vi和Pi为wi、vi和xi的 方 差;Ki为卡尔曼增益,是观测和预测的加权系数。
2.2.2 递减平均法
递减平均法(Decaying Average,DA)[6]是基于卡尔曼滤波原理发展的自适应偏差订正方法,它通过对不同时段预报偏差的加权平均和迭代更新来估计订正时刻的递减平均偏差, 从而进行偏差订正。 它具有卡尔曼滤波的优点,同时参数更少。其公式如下:
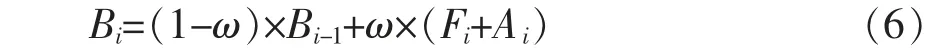
式中,i 代表时间;Bi、Fi和Ai分别为偏差订正值、预报值和分析值;ω 为递减平均权重参数。
本文采用上述两种滤波方法, 利用预报和实况样本数据, 针对每个格点上0—24 时的气温和相对湿度,均建立该要素的两种滤波订正模型,分别称为KF 模型和DA 模型,选取其中拟合效果更好的模型作为最终的预报模型。期间,为了验证滤波模型效果,构建了一元线性回归预报模型(以下简称回归模型或LR 模型)进行对比。
2.3 检验方法
依据《全国智能网格陆面基本要素预报检验办 法 (2017 年)》, 采 用 平 均 绝 对 误 差(Mean Absolute Deviation,MAE) 和 均 方 根 误 差(Root Mean Square Error,RMSE)对模型进行检验。 其公式如下:

式中,n 为样本数;Oj和Pj分别为观测值和预报值。
3 模型的拟合效果
3.1 模型的误差平均值
采用构建的两种滤波模型、LR 模型和WRF模式,进行气温和相对湿度的预报拟合,计算全部格点和时次的平均值, 得到各种方法的误差平均值(图1)。 由图1 可知,两种滤波模型对气温和相对湿度的预报误差均明显小于WRF 模式和LR模型的预报误差。 其中, 气温预报的MAE 和RMSE 在3~4℃, 相对湿度预报的MAE 和RMSE在20%以下。与WRF 模式相比,KF 模型的气温预报MAE 和RMSE 分别下降1.3℃和1.7℃,相对湿度预报MAE 和RMSE 分别下降8.6%和9.5%;DA模型的气温预报MAE 和RMSE 分别下降1.5℃和1.8℃, 相对湿度预报MAE 和RMSE 分别下降11.0%和11.6%。

图1 试验模型对全部格点全部时次的气温(单位:℃)、相对湿度(单位:%)预报拟合效果
根据逐小时预报的格点平均误差统计(图2),WRF 模式预报误差具有明显的日变化特征,滤波模型的误差同样表现出日变化特征, 但时间变化相对更小,且各时次的误差均明显小于WRF 模式误差,说明滤波模型能显著订正WRF 模式的系统性偏差;DA 模型的订正效果更好。 其中,WRF 模式在傍晚时段(17—18 时)的预报误差最大,而两种滤波模型在该时段的误差订正效果最为显著。另外,两种滤波模型对08 时气温的预报误差相对最小;KF 模型和DA 模型对相对湿度的预报误差最小时段分别约为04 时前后和10 时前后。
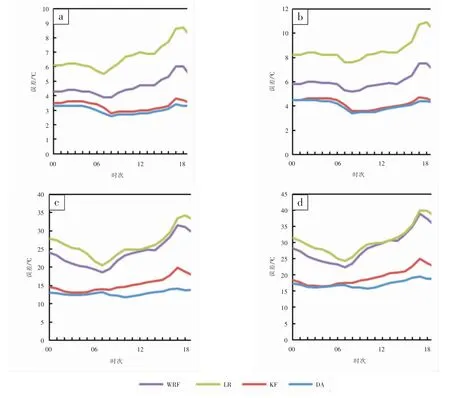
图2 试验模型对全部格点逐小时气温预报的MAE(a)、RMSE(b)和相对湿度预报的MAE(c)、RMSE(d)
3.2 模型对随机格点和时次的预报拟合效果
采用滤波模型对随机选取的某一格点某一时次的气温和相对湿度进行预报拟合, 并与LR 模型、WRF 模式预报和实况分析值进行对比。 根据拟合情况(图3)来看,即便在WRF 模式具有较大预报误差的情况下,滤波模型(尤其是DA 模型)也能够通过快速调整,达到与气温实况基本重合;对于相对湿度,无论在偏湿还是偏干阶段(即有无降水时),都是DA 模型的预报与实况最为接近。

图3 试验模型对随机格点和时次的气温(a)和相对湿度(b)预报拟合情况
4 模型的试报效果
上述拟合结果表明, 两种卡尔曼滤波模型均优于原始模式和回归模型。 其中,DA 模型的拟合效果更好,因此,选取其作为预报模型。 采用预报模型、试报样本,对全部格点逐小时的气温和相对湿度进行试报, 并与WRF 模式预报进行对比,得到预报的日变化曲线(图4)。 由图4 可见,预报模型对气温预报的误差订正在中午 (12 时前后)表现最好; 对相对湿度预报的订正在早晨(03—08时)效果最好。 预报模型对气温预报的MAE 在大部分时段内均在2℃以内, 较WRF 模式的MAE降低了0.1~0.3℃; 相对湿度预报的MAE 基本在5%以下,较WRF 模式的MAE 降低了1%~3%。
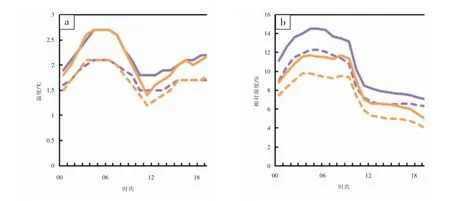
图4 预报模型对全部格点逐小时气温(a)、相对湿度(b)试报结果
值得注意的是,由于试报样本数量较少,滤波效果尚未调整到最佳水平。可以推测,在具备更多资料的情况下,模型预报误差仍有降低空间。
5 结语
本文基于卡尔曼滤波原理, 采用具有高时空分辨率的数值模式预报和格点实况数据, 对长春市气温和相对湿度的精细化网格预报进行了模式预报偏差订正建模试验。
(1) 试验建立了基于卡尔曼滤波方法的KF模型、 基于递减平均法的DA 模型。 根据拟合结果, 选取效果更好的DA 模型作为气温和相对湿度的格点化预报模型,模型的空间分辨率为3km×3km,时间分辨率为1h。
(2) 基于卡尔曼滤波原理建立的两种滤波模型,均具有显著的误差订正效果,能够订正原始模式的系统性偏差,且效果好于一元线性回归模型。其中, 基于递减平均法的DA 模型效果更好。 在WRF 模式具有较大预报误差的情况下,滤波模型(尤其是DA 模型)也能够通过快速调整,达到与实况基本重合。
(3)模型拟合过程中,相比WRF 模式,KF 模型的气温预报MAE 和RMSE 分别下降1.3 ℃和1.7℃, 相对湿度预报MAE 和RMSE 分别下降8.6%和9.5%;DA 模型的气温预报MAE 和RMSE分别下降1.5℃和1.8℃, 相对湿度预报MAE 和RMSE 分别下降11.0%和11.6%。
(4)选取DA 模型作为预报模型,进行试报,气温预报的MAE 在大部分时段内在2℃以内;相对湿度预报的MAE 基本在5%以下。
(5)需要指出的是,在试验过程中,CLDAS 和WRF 资料均有不同程度的缺失, 样本连续性对滤波效果有一定影响。 因此,采用具有较高连续性和完整性的资料,尤其是采用完整的全年资料,区分不同季节进行建模,将有助于提高模型的误差订正效果。此外,在针对格点化预报进行检验的过程中,可考虑采用邻域法替代本文采用的点对点检验方法。本文所建立的模型及其预报效果可以为进一步建立人工智能网格预报方法提供对比参照。

