分段循环荷载作用下二维非饱和土固结特性分析*
张 添 汪 磊 沈思东
(上海工程技术大学城市轨道交通学院,上海 201620,中国)
0 引 言
20世纪40年代起,国外学者围绕非饱和土固结开展了大量的研究:含有封闭气泡的非饱和土一般固结理论最先被提出(Biot,1941);孔隙比和饱和度的变化被引入了包含封闭气体的非饱和土固结模型(Scott,1963);Barden(1965)进行了压实非饱和黏土的一维固结分析;最具代表性的是Fredlund et al.(1979)的一维非饱和土固结理论,他提出的固结方程由气相、液相的两个连续方程组成,并给出了较为完善的非饱和土固结模型。近年来,非饱和土固结理论也成为了国内研究的热点:20世纪初,假定孔隙气排气率恒定的非饱和土简化固结理论被提出(沈珠江,2003);针对气体封闭的非饱和土模型,曹雪山等(2009)提出了仅考虑水压消散和将水、气视为混合流体的简化方法;周万欢等(2013)利用差分求积法研究了复杂初始和边界条件对一维非饱和土固结的影响;基于线性假定,汪磊(2017)得到了多种边界条件、任意荷载下一维和两维非饱和土固结方程的半解析解。非饱和土轴对称固结理论也已受到关注:秦爱芳等(2017,2019)对考虑涂抹区渗透系数变化及半渗透边界下非饱和土砂井地基的超孔隙压力进行了求解;随后,秦爱芳等(2020)对瞬时荷载作用下考虑井阻及涂抹作用下的非饱和土竖井地基固结方程进行了求解,并对固结过程中井阻因子和涂抹系数的影响进行了深入的研究。
实际的岩土工程经常会受到循环荷载的影响,如交通荷载、风浪荷载和储油罐荷载等,其具有典型的周期性和不连续性。分段循环荷载的形式主要有半正(余)弦、三角形、矩形和梯形等形式的分段循环荷载。连续循环荷载在同一周期内可以用单一的函数关系式表达,而分段循环荷载在同一周期不同阶段拥有不同的函数关系式,具有明显的随机性与不确定性,更接近实际工程中的荷载。循环荷载作用下的固结研究主要有:谢康和等(2006)建立了低频循环荷载作用下地基的一维固结方程;在给出了半正矢循环荷载作用下一维固结控制方程的半解析解后,Razouki et al.(2013)研究了荷载频率对固结特性的影响。虽然近年来相关学者已经在非饱和土循环荷载固结问题上取得了部分研究成果,但研究的荷载大多是连续循环荷载,缺少对分段循环荷载的研究分析。此外,为了提高固结排水速率,在铁路或公路路基施工中经常会在路基两侧设置砂井,土体中的孔隙水和孔隙气既可以沿竖直方向排出又可以通过侧向的砂井排出。因此,二维的非饱和土固结特性研究具有重要的现实意义。目前尚未出现对分段循环荷载作用下非饱和土二维固结模型的研究。本文给出了分段循环荷载作用下二维非饱和土固结的超孔隙压力和沉降的半解析解表达式,并研究了各类分段循环荷载作用下不同参数对沉降的影响,可为实际工程提供一定的理论指导和参考依据。
1 计算模型
1.1 控制方程
在Dakshanamurthy et al.(1980)提出的非饱和土固结理论基础上,设计一种新型的二维非饱和土固结模型,如图1所示,模型的深度为h、长度为l,q(t)为所研究的分段循环荷载。在该模型中,超孔隙气压力和超孔隙水压力沿水平方向(x轴方向)和竖直方向(z轴方向)同时消散。
该模型的主要假设如下:
(1)模型中非饱和土体是均质的;
(2)液相和气相连续且各自独立;
(3)固结过程中土的体积变化系数恒定;
(4)气相和液相的渗透系数均为定值;
(5)忽略空气在水中和水蒸气在土体中的运移等影响;
(6)土颗粒和孔隙水均不可压缩。
气相和液相的基本控制方程如下:
(1)
(2)
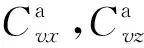
(3a)
(3b)
(3c)
(3d)
(3e)
(3f)
(3g)
(3h)
1.2 初始条件
(4a)
(4b)
1.3 边界条件
(1)顶面边界(z=0):
ua(x,0,t)=0
(5a)
uw(x,0,t)=0
(5b)
(2)底面边界(z=h):
(6a)
(6b)
(3)侧面边界(x=0)和(x=l):
ua(0,z,t)=ua(l,z,t)=0
(7a)
uw(0,z,t)=uw(l,z,t)=0
(7b)
模型顶面和侧面为透气透水边界,底面为不透气不透水边界。
1.4 荷载条件
常见的分段循环荷载主要有三角形荷载、矩形荷载和梯形荷载。
图2中T代表分段循环荷载周期,m、n为正整数,qmax为荷载最大值,q0为荷载初值。
三角形荷载如图2a所示,表达式如式(8a),对固结模型线性加载T/2时间,荷载特征参数为a1,加载后按相同速率卸载。
矩形荷载如图2b所示,对模型持续施加恒定荷载qmax后循环骤减骤加过程,表达式如式(8b)。值得指出的是矩形荷载初值假定为qmax。
梯形荷载如图2c所示,荷载特征参数为a2,线性加载mT后,持续(1-2m)T保持qmax加载,以同样速率卸载,表达式如式(8c)。
(8a)
(8b)
(8c)
此外,荷载特征参数即qmax与加载天数的比值。矩形循环荷载无线性加、卸载的过程,荷载特征参数体现为周期。
2 求解和验证
2.1 控制方程的求解
由于侧面边界可透气、透水,因此x方向可用Fourier正弦级数表示,此时ua和uw可转化为:
(9)
(10)
将式(9)和式(10)分别对t求一阶和二阶导后分别代入式(1)和式(2)可得:
(11)
(12)
根据正弦函数的正交性,式(11)和式(12)可转化为:
(13)
(14)
对式(13)和式(14)进行Laplace变换,整理得:
(15)
(16)
对式(14)求关于z的二阶导,得:
(17)
将式(14)和式(17)代入(15)得:
(18)
解四阶微分方程式(18)得:
(19)
U~w=a5C1eξz+a5C2e-ξz+a6D1eηz+a6D2e-ηz+a7
(20)
式(19)和式(20)分别为固结过程中超孔隙气压力和超孔隙水压力在Laplace域内的通解。C1,C2,D1和D2是关于n和s的任意函数,由边界条件决定。将式(19)和式(20)及其关于z的一阶导数代入边界条件,整理得:
(21)
(22)
对式(9)和式(10)进行Laplace变换并结合式(21)和式(22)即得到Laplace域中控制方程的通解:
(23)
(24)
二维固结模型下体变可表示为:
(25)
将式(25)进行Laplace变换得:
(26)
在Laplace域中,沉降可表达为:
(27)
结合式(23)、式(24)、式(26)和式(27)得:
(28)
(29)
(30)
(31)
式中:tj=jΔt=jT/N,j=0,1,2,…,N-1,T为总的计算时段;N为总的计算步数,对于L×N=50~5000,当aT=5~10时,计算结果较好,且稳定。本文采用此方法得到的半解析解与解析解进行了验证对比,精度较高,缺点是当时间较小时无法计算出结果,可以通过延长计算时段取特定时刻的结果解决。
(32a)
(32b)
(32c)
2.2 退化法验证
为了验证所推导的半解析解的正确性,将非饱和土二维固结的半解析解退化为顶面透气透水、底面不透气不透水边界下一维固结问题的半解析解。此时,固结模型中横向的体积变化系数和气相与液相的渗透系数均为0。结合一维体变可得到退化后的非饱和土一维固结的沉降表达式如式(33):
(33)
然后,采用经典算例进行验证,参数取值与文献(秦爱芳等,2008)相同。图3为所得半解析解结果(缩写为SAS)与文献中解析解结果(缩写为AS)的对比。显然两者结果一致,验证了本文半解析解的正确性。
3 算例和分析
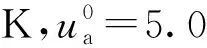
非饱和土的固结特性通常由ua,uw及由此推导的固结度(U)和沉降(w)体现,各项参数中渗透参数k对ua和uw中影响最大。由于气相的存在才造成了非饱和土结构的复杂性,而二维的固结模型与一维相比则是增加了气相与液相在x方向的流动。此外,分段循环荷载的变化通过荷载特征参数a体现。因此本文选用ka/kw、kx/kz和荷载特征参数a分析固结特性。
需要指出的是:
(1)当研究ka/kw对分段循环荷载作用下二维平面应变固结的影响时,ka为变量,kw为定值,此时ka/kw=kax/kwx=kaz/kwz。
(2)当研究kx/kz对固结沉降的影响时,kz保持不变,kx是变量,此时kx/kz=kax/kaz=kwx/kwz。
(3)当研究荷载特征参数a对固结沉降的影响时,假定ka/kw=kx/kz=1,荷载周期分别取4id,40id,400id,荷载特征参数对应求得。
此外,在3种荷载作用下研究不同参数取值对固结的影响时,模型的计算点设为x=1im,z=1im。
3.1 三角循环荷载作用下的固结特性
本节研究三角形循环荷载作用下二维非饱和土的固结特性。结合式(31)和式(32a)可以求出三角形循环荷载作用下二维平面应变固结的沉降值。
图4a为三角形荷载作用下ka/kw变化时沉降的发展曲线。沉降发展的前期主要由超孔隙气压力的消散造成,超孔隙气压力的消散随着ka/kw的增大加快,沉降发展的速度也加快,曲线波动的振幅增大。沉降的后期主要由超孔隙水压力消散引起,当ka/kw>10时,ka对沉降后期超孔隙水压力的消散无明显影响,所以后期的曲线振幅差异不明显。
图4b中可以看出kx/kz的增大将加速固结,使得沉降曲线振幅波动变大,第1次峰值出现在106is后。kx/kz≤1时,kx对后期超孔隙压力消散影响较小,沉降的差异也较小。
图4c是渗透系数一定时,荷载特征参数a1变化引起的三角形荷载作用下固结沉降规律曲线。由于a1与加载的时间有关,所以a1的变化直接影响了沉降发展的起始时间。a1越大,沉降在荷载斜坡期增长越快,曲线振幅越小。
3.2 矩形循环荷载作用下的固结特性
由式(31)和式(32b)可以得到矩形循环荷载作用下二维固结的沉降。由于矩形荷载初始值为qmax之后在qmax至q0间循环,而三角形与梯形荷载相反,所以矩形荷载作用下的沉降曲线会呈现出与其余两种荷载作用下不同的规律。
图5a描绘了矩形荷载作用下不同ka/kw引起的沉降差异。当ka/kw=100时,前期超孔隙气压力消散较快,沉降较大。
从图5b中可以看出横向与竖向渗透参数比值kx/kz越大,沉降值越大。
矩形循环荷载中荷载参数的变化体现荷载周期的变化。如图5c,渗透系数一定时,当周期取值最小即T=3.456×105is时,沉降最早发生,相应的值也最小。
3.3 梯形循环荷载作用下的固结特性
由式(31)和式(32c)可以得出梯形荷载作用下二维平面应变固结的沉降结果。
图6a为荷载特征参数a=2.315×10-4ikPa·s时,不同ka/kw引起的沉降变化曲线。结果表明,ka/kw越大,沉降发展越快,最终曲线振幅越大。
图6b中体现了不同kx/kz对沉降的影响,随着kx/kz的增大,曲线振幅逐渐减大。此外,kx/kz≤1时,同样存在沉降差异不明显的规律。
从图6c中可以明显看出在渗透系数ka/kw=1,kx/kz=1时,不同荷载特征参数引起的沉降起始时间差异明显。如图6,参数a2越大,沉降起始越早,沉降量越小,与三角形荷载拥有相同的规律。
4 结 论
(1)各种类型的分段循环荷载对固结过程均有显著影响,沉降发展的周期与荷载施加的周期一致,沉降发展的特征与荷载的特征一致。
(2)在相同的情况下,ka/kw越大,超孔隙气压力消散越快,沉降越显著;而kx/kz的增大使得非饱和土体各向异性更加明显,加速了固结进程,沉降量增大,因此水平方向的渗透性在二维非饱和土固结过程中起到了十分重要的作用。
(3)荷载特征参数直接影响沉降发展的起始时间,因此在实际施工过程中可以通过改变施工速度来控制非饱和土体的固结沉降过程。

