极端值条件下线性回归分析策略的模拟研究

胡维维 李业棉 颜 虹 陈方尧

西安交通大学公共卫生学院流行病与卫生统计学系卫生统计教研室，710061 陕西 西安

极端值是指数据中出现的极大或极小值，它们通常偏离数据的主体位置较远，在实践中又可分为单变量和多变量极端值[1]。研究设计存在的缺陷、统计调查与分析的错误、样本本身的变异等均可导致极端值的产生。随着样本量的增加，极端值的出现往往是一个难以避免的问题，常常可能导致统计分析结果出现较大的偏差和错误[2]。

在统计分析实践中，在研究事物间的复杂关联时，多因素回归分析有着广泛的应用[3]。多因素线性回归模型的参数估计通常使用最小二乘法(ordinary least squares，OLS)，通过最小化误差的平方和来寻找最佳函数匹配，OLS估计法假定每一个样本点对建立线性回归模型的贡献是均匀的[4-5]。OLS估计法对数据中的极端值点是十分敏感的，极端值点往往不能满足OLS估计的假定，进而出现少数极端值点支配线性回归模型建模结果的情况，使分析结果出现较大的偏倚。

目前，对于多因素回归分析中极端值点的处理已发展出了多种策略，但对于各种不同的极端值情况，在进行多因素回归分析时应选用哪一种处理策略更为合适，目前并没有统一的认识。本研究旨在通过Monte Carlo模拟的方法，探讨在不同极端值条件下，各种极端值处理策略对于多因素线性回归分析结果准确性的影响，为多因素回归分析中极端值处理策略的选择提供参考依据。

1 线性回归极端值检测及常用极端值处理方法简介

1.1 线性回归中的极端值检测方法

在线性回归模型中，极端值通常包含了离群点(outlier points)、高杠杆值点(high leverage points)和强影响点(influential points)。离群点是指一组数据中与主体距离较远的观测点，主要使用学生化残差(studentized residuals)进行判定，学生化残差绝对值大于等于3，则可认定其为离群点[6]。高杠杆值点是由许多异常的预测变量值组合起来的，与响应变量值没有关系，常使用帽子统计量(hat values)来判断杠杆值，通常以一个观测点的帽子值大于帽子均值的2倍到3倍为标准判定。强影响点指对回归模型有较大影响的样本点，常用Cook距离(Cook′s distance)来判断，具有较大Cook距离的观测点可能为强影响点[7]。

本研究使用了统计软件R语言中的“car”包提供的influencePlot函数，来计算学生化残差、hat值和Cook距离，从而检测出极端值点。

1.2 线性回归中常用极端值处理方法

1.2.1 直接删除极端值

在线性回归分析中，在数据中极端值点数量很少或所占比例很低时，直接删除极端值并不会对回归模型的参数估计产生大的影响，也不会损失有用的信息，是一种十分常用且操作简便的极端值处理策略[8]；但盲目地删除极端值可能会降低统计效率或导致模型失真。

1.2.2 稳健回归(robust regression)

稳健回归是一种将稳健估计(robust estimation)的运算方法带入到回归分析中，以此来改善使用普通OLS法时对极端值十分敏感这一特性的回归分析方法[9-10]。稳健回归对于极端值的抵抗性更好，可得到更接近于真实值的分析结果。本研究使用的稳健MM估计法使用了一个以上的M估计程序来求解最终的估计量，具有高崩溃点(50%)和良好的效率(在高斯-马尔科夫假定下，效率约为OLS估计的95%)[11]。

1.2.3 多重插补(multi-imputation)

多重插补是一种基于重复模拟来处理缺失值的方法，其基于原有的数据集进行插补建模，可同时生成多个插补值，再进行模型整合与评价，最后构建出完整的数据集[12]。将极端值转换为缺失值再进行多重插补，插补数据对于构建回归模型有很好的估计效果，可极大减少极端值对模型参数估计的影响。

1.2.4 数据转换

对极端值进行数据转换，可在一定程度上减小数据的变异程度，改善极端值对回归分析模型估计的影响。对因变量方向上的极端值进行Box-Cox变换，对自变量方向上的极端值使用最小-最大标准化法，均可在一定程度上减小极端值所带来的变异[13-14]。

2 模拟研究

2.1 模拟研究设计

模拟研究基于R语言实现，含极端值的模拟数据基于Monte Carlo方法产生。设存在2个服从正态分布的自变量X1和X2，X1～N(8,2.52)，X2～N(9,2.82)。

假设因变量Y为服从正态分布的随机变量，且Y与自变量间的关系，由线性回归模型Y=β0+β1X1+β2X2+ε来确定。回归方程变量的系数设为截距项β0=15，回归系数项β1=2,β2=1.5。模拟研究同时(在原假设下)产生了2个与Y无关的干扰变量X3～N(4,1.32),X4～N(6,1.92)，测试在采用不同的极端值处理方法时，对回归模型正确筛选变量能力的影响。

产生极端值时，以需要产生极端值的变量所服从正态分布的总体参数μ为基础，首先产生在其总体均值基础上增加3～4倍标准差范围内的均匀分布U(μ+3σ,μ+4σ)，然后从中随机抽样产生相应的极端值，最后随机替换该变量中最初产生的非极端观测值。

模拟研究样本量取50、100、200和400，每样本中的极端值比例取5%、10%和15%。极端值分别添加于X变量方向、Y变量方向以及X和Y变量方向3种情况。每一个参数组合下，进行1 000次模拟。

考虑到实际应用中随机误差项并不一定服从标准正态分布，本研究第一部分模拟中设置ε～N(0,42)，使模型R2在0.7左右。本研究第二部分模拟中，在样本量为100的条件下，测试了不同的随机误差项标准差水平下，即σ=2,4,6的条件下，各种极端值处理策略的表现。

模拟评价指标包括：Ⅰ类错误概率α，即纳入了实际上不应该被纳入回归模型变量的概率，α水平越接近设定检验水准0.05越好；Ⅱ类错误概率β，即未纳入实际上应该被纳入回归模型变量的概率，β水平越低越好；回归模型系数估计值的均方根误差(RMSE)，表示所求得模型回归系数与模拟数据所设定回归系数之间的偏差；回归模型的决定系数R2和调整R2，反映了回归方程的拟合效果。

2.2 模拟结果

在不同样本量、不同极端值比例和不同极端值方向的各种组合下，每种极端值情况均进行1 000次模拟。第一部分模拟中，在固定随机误差标准差水平下，得到各种极端值处理方法的性能表现见表1至表4。

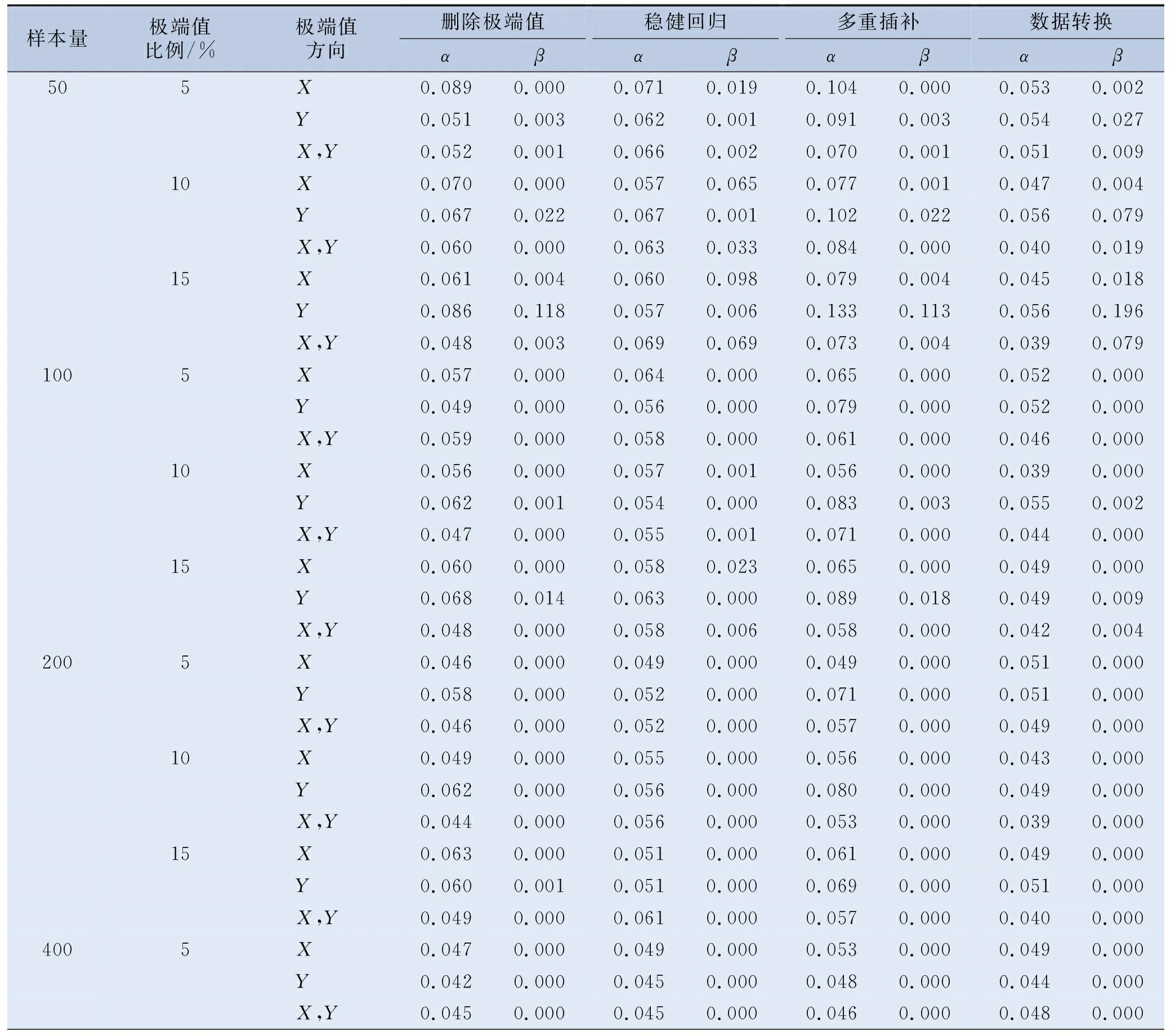
表1 线性回归中各种极端值处理策略的α和β水平

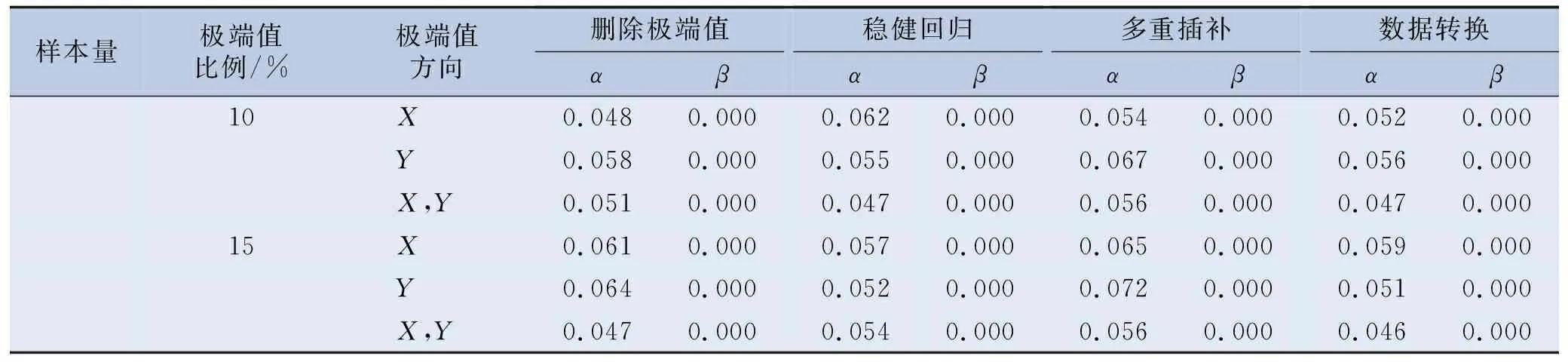
表1 (续)

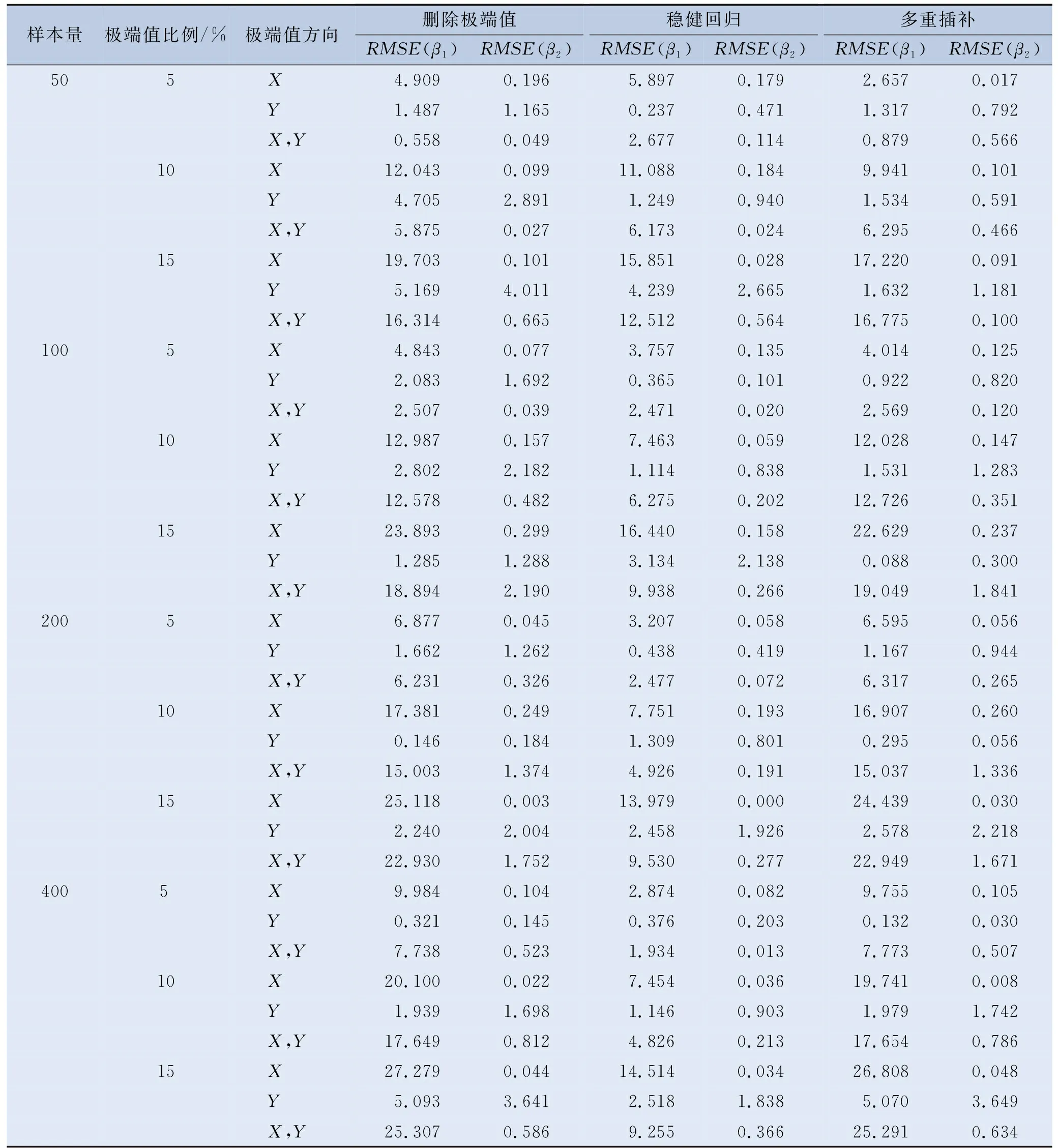
表2 线性回归中各种极端值处理策略的回归系数估计值RMSE

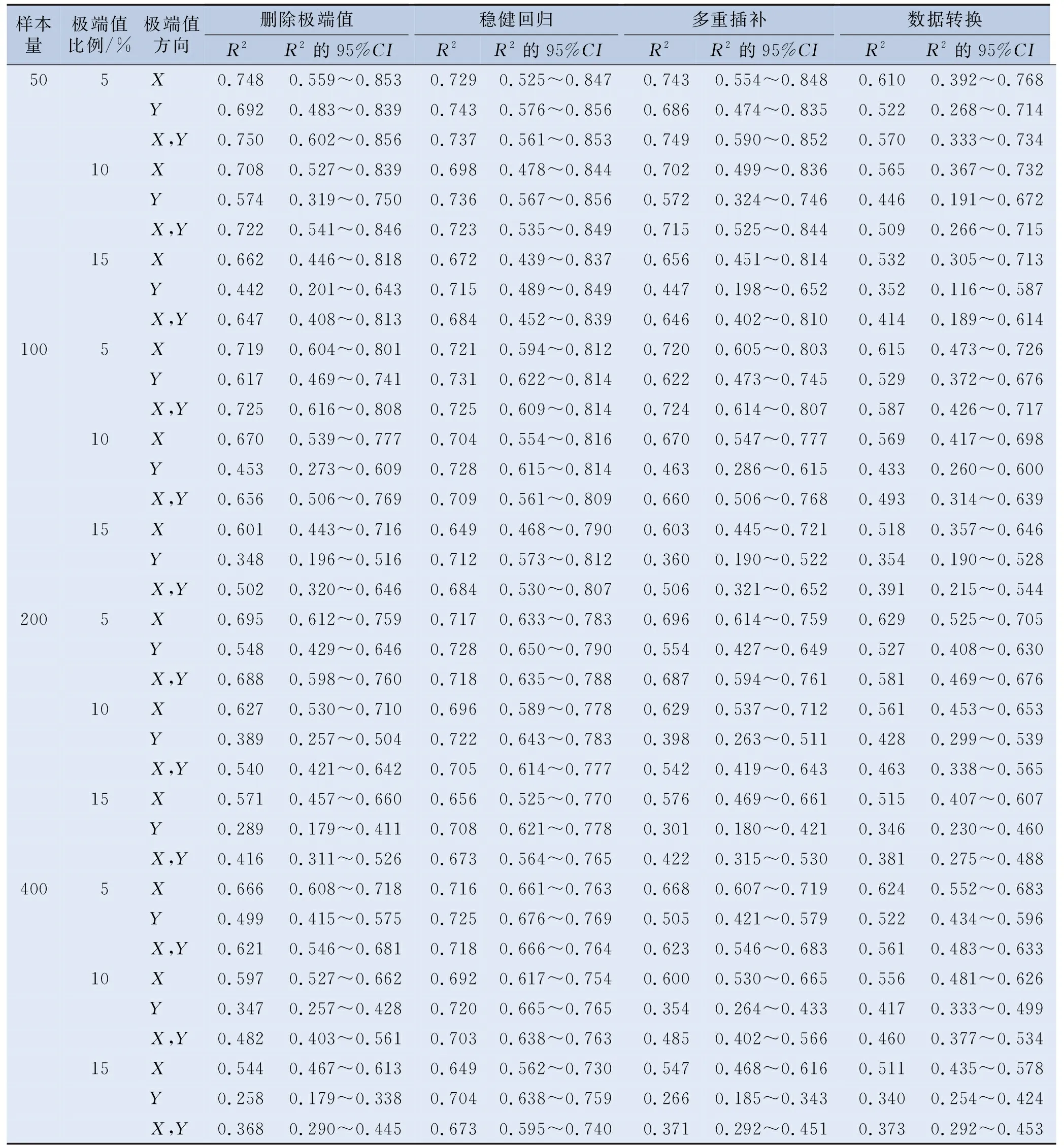
表3 线性回归中各种极端值处理策略的回归模型R2

表4 线性回归中各种极端值处理策略的回归模型调整R2

表1至表4的模拟结果显示,直接删除极端值法在数据集中含极端值的观测点数量较少和极端值比例较低时，其Ⅰ类错误概率α的水平更为接近0.05(预设水平)，且Ⅱ类错误概率β的水平也更低，结果准确性更好；模型自变量X1和X2系数估计值的RMSE更小，所得回归系数估计值更接近真实值；模型的决定系数R2和调整R2更为接近0.7，回归模型的拟合效果更好。

稳健回归法随着样本量的增大，Ⅰ类错误概率α的水平更为接近0.05，Ⅱ类错误概率β的水平也越来越低，纳入变量的准确性更好，在样本量相同和一定极端值比例内的情况下，稳健回归的结果准确性也几乎不受极端值比例变化的影响。稳健回归法在样本量足够时，模型自变量X1和X2系数估计值的RMSE更小，其所求得的回归系数与真实水平的误差越小，且样本量越大，其所求得结果的相对误差越小。稳健回归法在所设置的各种极端值条件下，所求得模型的决定系数R2和调整R2都达到了0.7左右的稳定较高水平，且随样本量的增大，其R2和调整R2轻微增大，模型拟合效果很好。

将极端值转换为缺失值再进行多重插补的方法，其在小样本量和较大极端值比例时Ⅰ类错误概率α水平与0.05差异较大，Ⅱ类错误概率β水平也较高，结果准确性差。多重插补法的系数估计值的RMSE有随样本量增大而逐渐增大的趋势，极端值比例越大，其相对误差也越大。其R2和调整R2随样本量和极端值比例的增大而逐渐减小，模型拟合效果逐渐变差。

对极端值进行数据转换法在各种极端值条件下，Ⅰ类错误概率α水平变化较大，Ⅱ类错误概率β水平较低，结果准确性在各种极端值条件下变化较大，且所得模型R2和调整R2都很小，模型拟合效果很不好。

第二部分模拟研究结果显示，在不同的σ条件下，随着σ的增大，模型拟合程度逐渐变差，各种极端值处理策略的性能均有很大程度的下降。见图1。

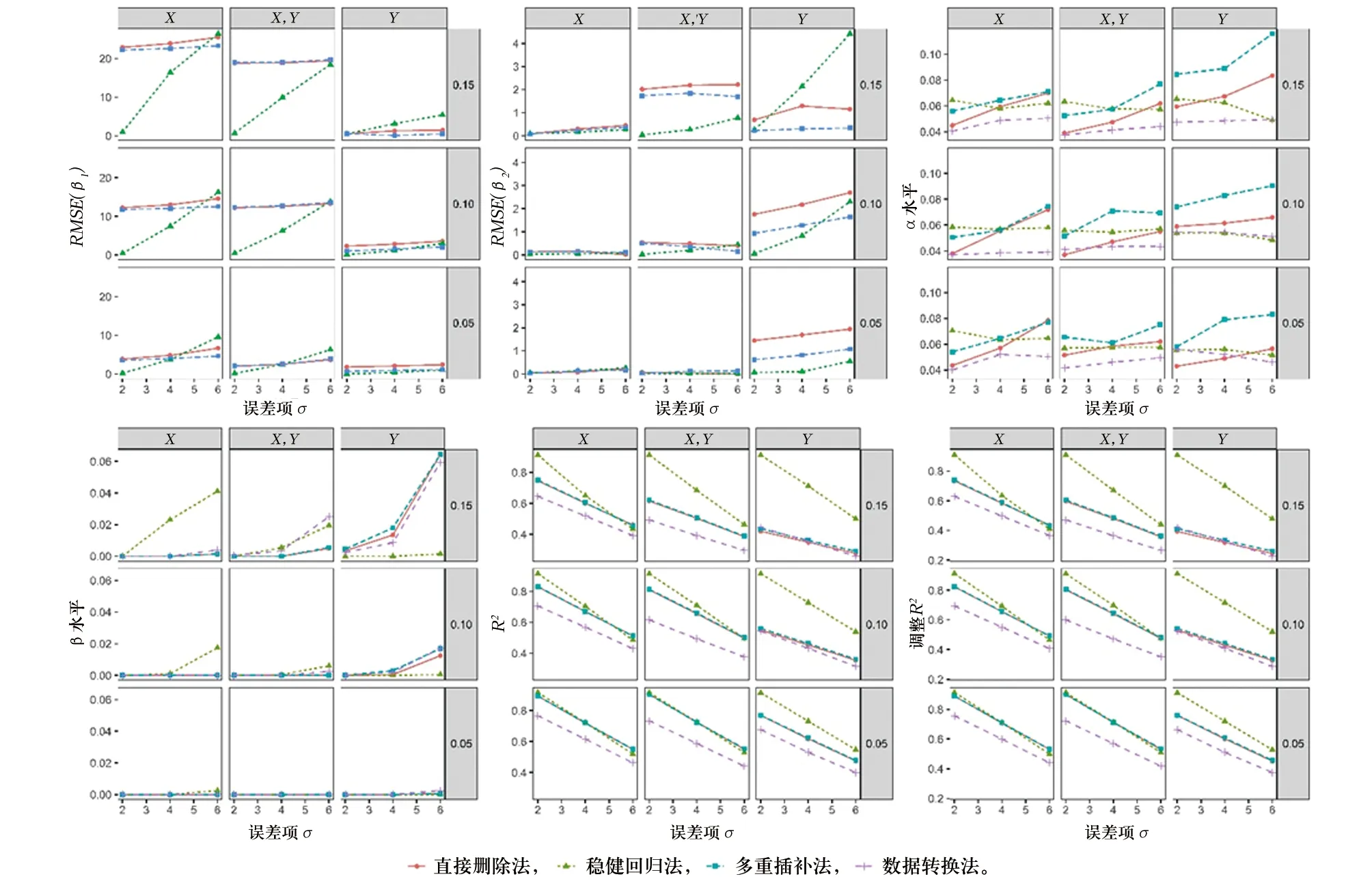
图1 样本量n=100时不同σ条件下各极端值处理策略的表现

总体来说，当随机误差项水平一定的条件下，多因素回归分析中对极端值进行处理时，样本量与极端值所占比例的影响很大。在极端值所占比例较小时，直接删除极端值法、稳健回归法和多重插补法的效果均有所提高，随着样本量增大，稳健回归法所得结果更稳定可靠，而直接删除极端值法和多重插补法的效果逐渐变差。模拟研究还发现极端值所在变量方向对极端值处理结果有轻微的影响。

在模拟研究中，稳健回归的方法在有足够样本量提供建模支持，极端值数量较少时，有更好的表现，且在其他极端值条件下也有很不错的表现，其模型系数估计值的相对误差较小，模型拟合效果也很好。多重插补法在含极端值的小样本量和极端值比例较小时有可接受的表现，随着样本量和极端值比例增大，其表现逐渐变差，但总体看来，极端值处理效果优于直接删除法。直接删除极端值的方法只在含极端值的观测点数量较少和极端值比例较小时有可接受的表现，其模型系数估计值的相对误差大小和拟合效果均比以上2种方法差，其只适合在极端值数量较少和所占比例较小时使用。数据转换的方法在所设置的极端值条件下均未见有较好的表现，其不适合在此次模拟的极端值情况中使用。

3 结论

模拟研究显示，在多因素回归分析中处理极端值时，推荐使用稳健回归分析的处理方法，此方法可很好地处理极端值并得到较为准确且拟合效果较好的回归模型，但在小样本量时需谨慎使用。多重插补的方法适用于极端值比例较小和模型拟合效果较好的数据，此时用插补值替代极端值较为可靠。对于直接删除极端值法，在专业角度上判断为异常点、含极端值观测点数量很少或极端值比例很低时可采用直接删除的方法，且并不推荐直接使用，可在其他处理方法未得到满意结果时再尝试使用。而数据转换的方法，并不适合大多数的极端值条件，可能只在某些少数特定极端值条件下适合使用。