面向智能制造车间的自动导引车调度优化算法研究
崔占鹏,王永军
(1.郑州工商学院 信息工程学院,郑州 451400;2.河南理工大学 计算机科学与技术学院,焦作 454000)
0 引言
制造业作为国民经济的重要支柱,代表着一个国家的科学技术和产业力量。在激烈的市场竞争和不断更新的情况下,现代制造面对着单件、小批量、个性化定制等多种生产形式,提出了敏捷制造、准时制造、智能制造等模式。自动导引车具有半自动化和全自动两种运输作业,它能使物料的搬运和装卸实现自动化[1]。目前,自动导引车已被广泛地用于自动化仓储、物流搬运、智能制造车间等各个方面。为满足智能制造车间的作业任务,对于自动导引车的调度优化研究成为了热点问题。
李西兴[2]等采用混合遗传鲸鱼优化算法,实现了柔性车间的自动引导车的融合调度。本文利用了基于工序排序和机械选取两个问题的二次矢量化编码方法,给出了以优先业务为基础的自动引导车调度算法。提出了一种基于离散化改进鲸鱼优化算法的群体初始化方法。采用了基于遗传算法的交叉和变异运算,结合了基于局部搜索的方法,实现了融合调度模型求解。该方法的融合调度效果较好,但调度效率较低。苏少春[3]等采用多目标狼群算法,研究了多模型自动导引车的路线优选问题。对自动导引车的航向规划问题进行了分析,提出了多个最优解,并对自动导引车的两级航迹进行了详细的设计。将狼群算法应用于非支配状态的狼群群体中,采用群体的数量来维持群体的差异,从而提高了多目标的性能,由此实现多模型自动导引车的路线优选。该方法能够有效实现自动导引车运行路线规划,但调度效果有待提高。针对上述问题,提出了面向智能制造车间的自动导引车调度优化算法。
1 智能制造车间自动导引车调度优化算法
1.1 自动导引车调度优化模型构建
为有效实现智能制造车间自动导引车调度优化,确保自动导引车行驶距离最短。首先,构建自动导引车调度优化模型。
假设存在一个任务指定位置集Q⊆W,W表示任务点集合,则将该任务指定位置集的总任务量描述为:

当自动导引车完成作业任务后,则返回作业起点,通过本文模型,获取自动导引车行驶距离最短的路线。假设变量表示为自动导引车e从任务点i行驶至任务点j;变量表示为未行驶到任务点的情况。由此,可构建的自动导引车调度优化模型如下:
目标函数为:

式(2)中,R为自动导引车集合,wij为任务点i至任务点j的行驶消耗,其中包括行驶的时间和距离。
约束条件为:
1)自动引导车装载数量的约束:

式(3)中,ti表示为任务点i的总任务量,P表示为自动导引车任务点具备数量。
2)每一个任务点只能进行一次访问的约束:

3)从作业起点到任务点后,无自动导引车重新回到作业起点的约束:
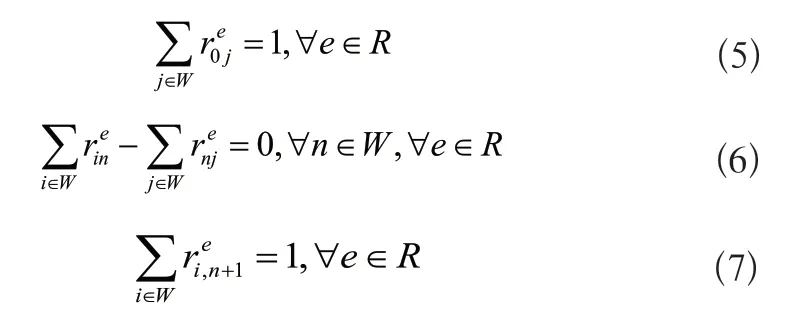
4)路径选择的约束:

通过设置不同的参数,可以将自动导引车的优化模型转化为组合优化问题。假定使用了某辆自动引导车,这个问题可以转化为旅行商问题(TSP)模型。
若附加约束条件g0=GH,GH≤gi≤JH,其中,gi表示为自动导引车达到任务点的时间,[GH,JH]表示为实现每项任务的时间范围。假设继续附加约束其中,Tij为任务点i与任务点j之间的运输时间,为自动导引车e行驶至任务点i的起始时间,则可获取包含时间窗的自动导引车调度优化问题的数学模型。
1.2 自动导引车调度优化模型求解
在构建自动导引车调度优化模型后,采用递归神经网络[4]对自动导引车调度优化模型进行求解。具体步骤如下:
1)相邻矩阵构造:利用网络节点,绘制了自动导引车起始点、经过路口和停车点,并用抽象的边线将各点上的有向路径相联系,提出了一个有向图表示为:

式(9)中,X为边数,Z为节点数,C为节点数的矩阵。
根据上述自动导引车调度优化模型可知,需要最优目标是边(i,j)的长度和时间,从而构造了距离和时间的相邻矩阵。
2)约束处理:在此基础上,提出了一种基于递归神经网络的能量函数的自动导引车调度优化模型,并在各能量方程中加入了一条惩罚项完成约束处理,从而使得约束能量在网络中的持续收敛得到了较好的稳定性。
设定pω为任务点所需量,ξ,ζ为运输顺序,运输点为ω,ϖ。
假定每一行和每一列只有1个,而且不包含0行,也就是说,当自动导引车经过一次任务点,并且必须经过一次时,返回作业起点的约束为:


假定0行中所有列的数值之和是B,也就是说,运输的路径数目是B,那么,有约束如下:

假定整个矩阵中的每一个单位的总和是V+B,作业起点的起始数目是τ,那么,有约束如下:

假定自动导引车的作业起点是一个物料任务点,那么,有约束如下:

假定自动导引车有负荷约束,并且每个自动导引车都有装载极限D,当满足极限条件时,将返回任务点,那么,有约束如下:

3)递归神经网络计算:假定相邻矩阵中的每个单元都对应于一个神经元,并设置了Vωξ是在(ω,ξ)点处的输出数值。在此基础上,首先求出了递归神经网络的能量函数,并对其进行了能量分析,得到了神经元的传输和状态转换方程,并对其进行了连续的迭代,得到了网络的收敛性。其能量函数表示为:

当得到能量函数后,由于该神经网络是以梯度的形式实现,因此,需通过以下形式计算神经元的传递函数与状态转移方程表示为:
在获得了能量函数之后,由于递归神经网络采用了梯度结构,需要表达神经元的传输函数和状态转换,在(ω,ξ)点处的输出数值表示为:

4)调度优化方案制定:通过对递归神经网络的收敛性分析,可以形成以0和1为单位的移位阵列。在该阵列中,自动导引车通过的节点为1,将各节点之间的距离和运输时间相加,可以得到最短的距离和时间。根据上述条件,可获得面向智能制造车间的自动导引车调度优化方案。
1.3 自动导引车调度优化实现
在对自动导引车调度优化模型进行求解的基础上,利用模拟退火算法[5],实现自动导引车调度优化。基于模拟退火算法的自动导引车调度优化算法流程如图1所示。

图1 基于模拟退火算法的自动导引车调度优化算法流程
步骤1:对较高温度T和自动导引车运输路径数目B进行初始化,设定温度T的迭代次数为U;
步骤2:对初始自动导引车运输路径数目扰动产生新解ι;
步骤3:计算自动导引车运输路径长度的差为:

步骤4:如果Δϑ<0,接受新路线解ι,否则以为新解的接受概率。
步骤5:当迭代次数达到U时,新路线解ι没有接受,则算法结束,输出最优自动导引车调度路线;否则T减少,返回步骤2。通过上述步骤,由此实现自动导引车调度优化。
2 实验分析
2.1 实验环境设置
为了验证面向智能制造车间的自动导引车调度优化算法的有效性。实验在Intel(R) Core(TM) i5-4570 CPU @3.20GHz CPU的计算机上测得,在Windows 7系统环境下,将MATLAB仿真平台作为实验环境。以某智能制造车间的自动导引车作为研究对象,分别采用文献[2]算法、文献[3]算法和所提算法进行对比,对上述自动导引车调度优化模型的实现过程进行验证。
2.2 自动导引车调度优化效果对比分析
为验证所提算法的自动导引车调度优化效果,基于上述设置的实验环境,选取2个任务点,得到不同算法从物料运输点到达任务点的调度路线,对比分析结果如图2所示。
分析图2可知,不同算法从物料运输点到达2个任务点的调度路线均有所不同。其中,文献[2]算法从物料运输点到达2个任务点的调度路线最远,规划后的路径距离最远,该调度路线呈现出曲线形状。文献[3]算法从物料运输点到达2个任务点的调度路线明显短于文献[2]算法从物料运输点到达2个任务点的调度路线,说明文献[3]算法在从物料运输点到达任务点的调度路线时,能够有效缩短调度路径。而相对于文献[2]算法和文献[3]算法,所提算法从物料运输点到达2个任务点的调度路线最短,且均呈现出直线的形式。由此可知,所提算法的自动导引车调度优化效果较好。
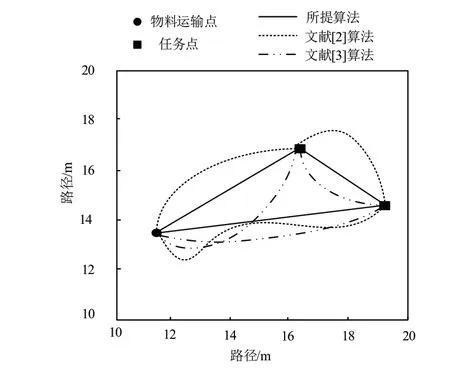
图2 不同算法从物料运输点到达任务点的调度路线
2.3 自动导引车调度优化路径长度对比分析
进一步验证所提算法的自动导引车调度优化路径长度,选取5个任务点进行自动导引车调度优化,得到不同算法的自动导引车调度优化路径长度,对比分析结果如图3所示。

图3 不同算法的自动导引车调度优化路径长度
分析图3可知,随着任务点的增加,不同算法的自动导引车调度优化路径长度随之增加。当任务点为5个时,文献[2]算法的自动导引车调度优化路径长度为3760m,文献[3]算法的自动导引车调度优化路径长度为5780m。而所提算法的自动导引车调度优化路径长度仅为988m。由此可知,所提算法的自动导引车调度优化路径长度较短。
2.4 自动导引车调度优化效率对比分析
在此基础上,验证所提算法的自动导引车调度优化效率,将自动导引车调度优化时间作为评价指标,其自动导引车调度优化时间越短,表明算法的自动导引车调度优化效率越高。得到不同算法的自动导引车调度优化时间,对比分析结果如表1所示。
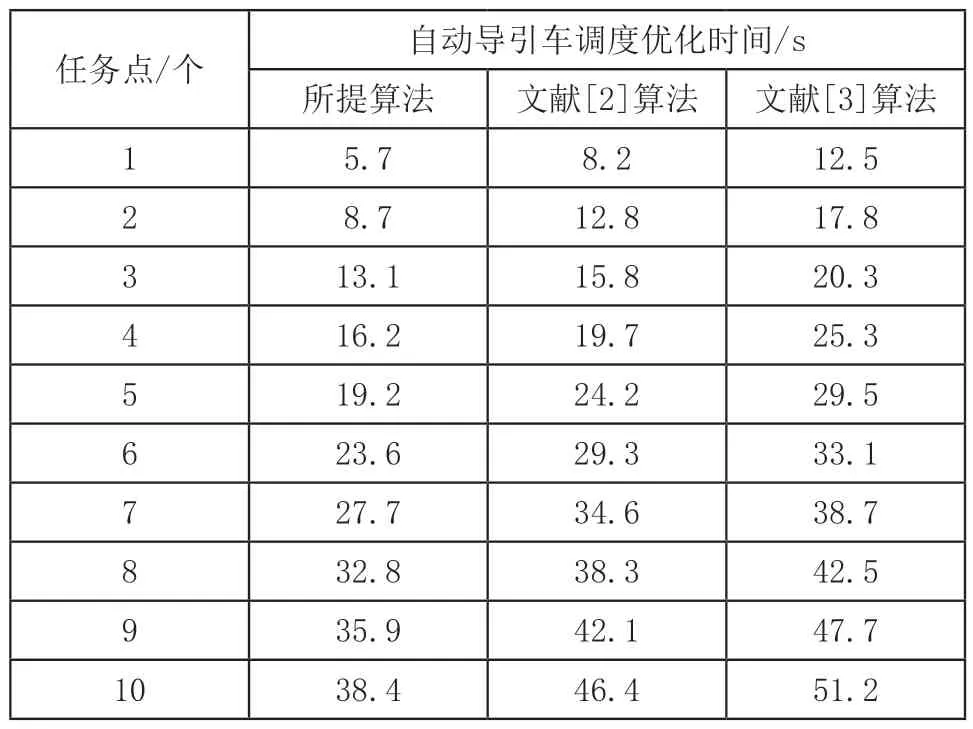
表1 不同算法的自动导引车调度优化时间
根据表1可知,随着任务点的增加,不同算法的自动导引车调度优化时间随之增加。当任务点为10个时,文献[2]算法的自动导引车调度优化时间为46.4s,文献[3]算法的自动导引车调度优化时间为51.2s,而所提算法的自动导引车调度优化时间仅为38.4s。由此可知,所提算法的自动导引车调度优化时间较短,能够有效提高自动导引车调度优化效率。
3 结语
针对智能制造车间存在的自动导引车调度优化路径长、效果差和效率低下的问题,研究了面向智能制造车间的自动导引车调度优化算法。通过构建自动导引车调度优化模型,采用递归神经网络,求解自动导引车调度优化模型。在此基础上,利用模拟退火算法,实现自动导引车调度优化。所提算法的自动导引车调度优化效果较好,能够有效提高调度优化效率,缩短自动导引车调度优化路径长度。

