基于CGCS2000的宜昌2000坐标系建立方法

卢立

（1.宜昌市土地勘测规划院，湖北 宜昌 443000）

坐标作为描述地球表面物体空间位置的基础信息，被广泛应用于测绘、工程建设、水利、交通、航空、航海、石油、物探、地震监测、军事以及科学研究等领域，而坐标成果的产生离不开测绘基准。测绘基准是所有地理空间信息统一的起始坐标框架，是描述地球表面自然形态、人文信息、地理空间特征的参照系统。可以说，测绘基准是所有位置信息的源头和基础。测绘基准体系建设的完善与否，将直接影响国民经济和国防建设中与其休戚相关的方方面面。城市控制网坐标系最理想的是与国家网坐标系一致，但城市控制网要求将控制网边长归算到参考椭球面上高程归化和高斯正形投影的距离改化总和（长度变形）限制在一定数值内，才能满足城市大比例尺测图和市政工程施工放样的需要[1]。

1 投影长度变形分析

作为反映城市范围内空间点位相互关系的载体和平台，城市坐标系应满足城市平面控制网的相关特点。如何根据这些目的和要求合适地选择投影面和投影带，减小投影长度变形，以及如何经济合理地确立城市平面控制网的坐标系，尚无统一规定。在建立独立坐标系时应考虑测区的实际情况，本文将基于现代测量技术成果进行城市投影变形量化分析，从而科学决断独立坐标系建立方案。

1.1 高程归化改正

本文采用测距仪等手段进行地面量距。观测边长S0归算至参考椭球面，其长度会缩短ΔS，因此设观测边的平均大地高为Hm，地球平均曲率半径为R，则椭球面上的边长为：

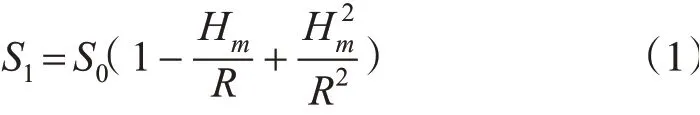
则由此引起的高程归化改正的近似关系为：

当R为6 371 km时，高程引起的长度变形如表1所示。

表1 高程引起的长度变形

1.2 高斯投影距离改正

椭球面上的边长S1投影至高斯平面，其长度S2将增加ΔS2，因此设该边两端点的横坐标平均值为ym，其差值为Δy，则由此引起的高斯投影距离改正的近似关系为[2-3]：

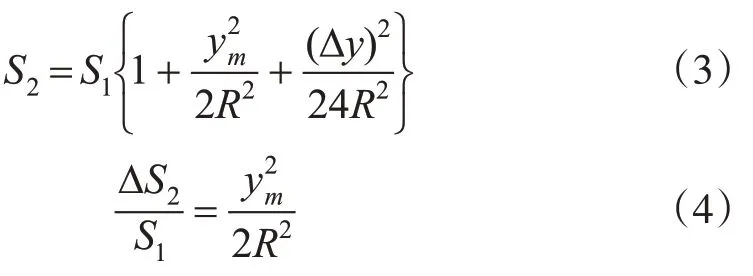
当ym为10～150 km时，高斯投影引起的每公里长度投影变形如表2所示。

表2 高斯投影引起的长度变形

2 常用独立坐标系建立方法

2.1 抵偿高程面上的高斯正形投影3°带坐标系

投影于抵偿高程面上的高斯正形投影3°带平面直角坐标系（以下简称抵偿坐标系）的中央子午线与国家统一坐标系3°带一致，但高程归算面不再是国家统一坐标系中的参考椭球面，而是依据高斯投影长度变形而选取的一个抵偿投影面。在抵偿坐标系中，并未减小高斯投影所引起的长度投影变形改正值，而是通过选取一个合适的高程面作为整个城市的高斯投影面，并利用由此引起的边长高程归化值来抵偿高斯投影改正值，该面即为抵偿投影面[4]。抵偿高程面的确立方法为：

若城市东西边缘横坐标值超出限值范围，虽采用抵偿坐标系，东西边缘的长度变形仍大于规定要求。由此可见，当城市中心远离3°带中央子午线时，离中央子午线越远，对城市东西宽度的限制就越严格，因此大型城市不宜采用抵偿坐标系。

2.2 任意带坐标系的高斯正形投影坐标系

在该类坐标系中，仍将地面观测结果归算到国家统一3°带坐标系所对应的参考椭球面上，但投影带的中央子午线不是国家统一的3°带中央子午线经线，而是为补偿高程归化长度变形而选择的某一条经线。此时，由于高程归算面不变，因此高程归化改正值亦不变，选择一条合适的经线作为中央子午线，再利用由此引起的边长高斯投影改正值来抵偿高程归化改正值[5]。其主要方法包括：①投影于参考椭球面的任意带坐标系；②投影于黄海平均海水面或城市平均高程面的任意带坐标系。

在该类坐标系中，把中央子午线移到城市中央，将高程归化面提高到该地区的平均高程面。当城市平均高程较低、城市平均高程面接近于黄海平均海水面时，也可选择黄海平均海水面作为高程归化面，这样既可使该测区的高程归化改正值和测区中央的投影变形几乎为零，又可保证在距离中央子午线东西各45 km以内的地区其投影变形的相对误差小于1/40 000。该方法通常适用于东西跨度小于90 km的城市建立独立坐标系。

2.3 投影于抵偿高程面的任意带坐标系

将城市平均高程面定为投影面而确定任意带坐标系的做法，尚不能体现任意带坐标系能适用于较大区域的优点。当城市范围较大时，可将抵偿高程面和任意带坐标系结合起来，确定投影于抵偿高程面的任意带坐标系，以期在较大区域内的投影长度变形仍满足规范要求，以适应现代城市规模不断扩大、城乡统筹规划与发展的需要。

3 宜昌2000坐标系的建立

宜昌市城区无论是离中央子午线距离还是平均海拔高，由高斯投影带来的长度变形量均偏大，甚至超过规范要求的限差。为减小投影长度变形误差、提高精度，主要遵循以下原则：①保证区域内地形起伏较小区域（即城市建设重点区域），各点投影长度变形值不大于2.5 cm/km；②对于某些地形变化较大的区域，投影长度变形不大于图根精度4 cm/km[6]。

3.1 实现思路

由于地形的复杂性，需根据不同的地形条件设置不同的坐标系，尽可能地使坐标控制范围不超限的区域面积最大，地形起伏较大时应顾及地势平缓山谷地区的投影变形。具体实现思路为：①提取宜昌市SRTM地形数据，并根据宜昌市各区边界裁切各区域的地形数据；②利用各区已有独立坐标系参数和SRTM地形数据，计算宜昌市各区内投影长度变形，并统计分析长度变形量；③若计算得到的投影变形达到独立坐标系建立原则，即区域内尽可能满足投影变形小于2.5 cm/km，某些地形变化较大的区域，投影变形不大于图根精度4 cm/km，则仍采用已有的独立坐标系参数；④若区域内有较大面积的区域投影变形不满足独立坐标系建立要求，则在保持已有独立坐标系参数和成果不变的前提下，调整高程抵偿面和中央子午线，建立新的独立坐标系，新的独立坐标系顾及地形变化选取参数，并根据地形确定与原独立坐标系之间的界线，这样各区有一个或多个独立坐标系，每个独立坐标系对应一个区域；⑤建立各区独立坐标系后，相邻的独立坐标系若高程抵偿面接近，且中央子午线相距不远，则将两个区域合并为一个区域，并设定坐标参数，如图1所示。

图1 宜昌市2000独立坐标系的建立思路

3.2 方法分析

SRTM获取了60°N至60°S之间的雷达影像数据，进一步处理制成了DEM模型，即SRTM地形产品数据。该数据产品2003年开始公开发布，经过多次修订，目前的数据修订版本为V4.1版本。SRTM地形数据主要包括SRTM3和SRTM1两类，SRTM3的精度为3弧秒，即90 m一个点，包括非洲、北美、南美、欧亚、澳大利亚以及部分岛屿；SRTM1的精度为1弧秒，即30 m一个点，仅限美国地区。SRTM地形数据的高程基准为EGM96的大地水准面，平面基准为WGS84，标称绝对高程精度为±16 m，绝对平面精度为±20 m。

基于SRTM地形数据，本文获取宜昌市范围内空间分辨率为90 m的格网点地理坐标和高程信息，并分别计算各格网点的长度变形量。该方法具有的优势为：

1）数据精度高。SRTM地形数据的高程绝对精度优于±16 m，平面精度优于±20 m，确定的长度变形精度优于3 mm/km；而传统手段仅依赖平均海拔信息，其高程与测区真实高程分布可能存在较大差异，因而其长度变形精度不高。

2）可实现全区域长度变形量化分析。传统方法仅能利用测区平均海拔作近似变形分析，无法顾及区域内复杂的地理分布，如对于山地区域，地形起伏大，传统方法仅能获取全区域近似变形；而SRTM地形数据确定的区域内各点长度变形量化值精度高，从而可更加科学地决策分析。

3）可实现科学分区，优先保障主城区区域。利用SRTM地形数据，可特定选取任意多边形区域，确定高程抵偿面时，可优先保证城市主要经济地带变形小，次要区域适当放宽精度要求，实现重点区域优先保障，更突出坐标系为适应当地发展需求的基础属性。

3.3 投影长度变形分析

结合宜昌市现有地理特征，为了量化分析建立坐标系后的投影变形情况，选取合适的高程投影面和中央子午线，本文采用宜昌市范围SRTM的DEM数据（分辨率为90 m），分别选取111°标准3°带中央子午线和111.5°带中央子午线，通过高程逐渐增加循环的方式，计算不同方案条件下宜昌市范围内各点的投影长度变形。具体实施思路为：

1）当中央子午线分别为111°、111.5°时，在抵偿面高程为0～300 m的范围内，每10 m选取1次，计算区域内的投影变形量，结果分析如表3、4所示。

表3 宜昌城区长度变形统计表（L=111°）/%

2）分析比对各投影高程面下的区域变形指标，进而选取最优高程投影面[7]。长度投影变形分析如图2、3所示，其中红色表示超限负值，蓝色表示超限正值。

图2 宜昌城区长度变形分布图（H=0，L=111°）

3.4 基于CGCS2000的宜昌2000坐标系推荐方案

通过上述分析，本文建议按以下参数建立宜昌2000坐标系：参考椭球为CGCS2000椭球；中央子午线为111.5°，带宽3°；抵偿高程面为100 m。

表4 宜昌城区长度变形统计表（L=111.5°）/%

图3 宜昌城区长度变形分布图（H=100，L=111.5°）

4 结语

本文以宜昌城区为例，通过计算分析可知，在CGCS2000椭球下宜昌市若采用国家统一的高斯—克吕格3°带正形投影，保持中央子午线111°E不变，则有较大区域投影长度变形超限，无法满足规范规定和城市建设的需要，且施加抵偿高程后其长度变形反而更差；采用任意带中央子午线所形成的投影方案，可解决采用国家标准3°带第37带（中央子午线111°）投影所造成的宜昌市域大部分区域每公里长度投影变形值超限的历史遗留问题，相较而言，符合日常测绘工作习惯，方便城市控制网与大型工程施工控制网的衔接。

综上所述，本文结合宜昌城区的地形地貌特征，利用SRTM成果资料，通过计算分析得出了适合宜昌城区范围的基于CGCS2000的宜昌2000坐标系建立方案，为宜昌城区范围建立2000独立坐标系提供了一种可行的实施方案。