基于非局部低秩稀疏矩阵分解的低剂量脑灌注CT图像恢复方法
《中国脑卒中防治报告2019》指出脑卒中已经成为我国居民致死的第一诱因,每5位死者中就有1人死于脑卒中。脑灌注CT可以快速、准确、无创地获取常规CT检查所不能获得的脑灌注血流动力学参数,在脑卒中诊断方面取得了巨大成功。然而,脑灌注CT检查中需要对感兴趣层面进行重复动态扫描,使得患者接受的X射线辐射剂量过高,导致患者出现严重脱发、皮肤灼伤、头痛等问题。为了增强脑灌注CT成像的临床生命力,优化控制X射线辐射剂量已经成为灌注CT成像领域亟待解决的关键问题。
采用SPSS 19.0统计学软件对数据进行处理,计量资料以“±s”表示,采用t检验,计数资料以百分数(%)表示,采用x2检验。以P<0.05为差异有统计学意义。
降低管电流或管电压是实现低剂量脑灌注CT成像最为简单有效的方法,但会导致传统滤波反投影算法重建的图像中含有大量的噪声和伪影,进而会影响到脑血流动力学参数图的准确性。目前,低剂量脑灌注CT成像方法主要分为两类:低剂量脑灌注CT图像重建方法和低剂量脑灌注CT图像后处理方法。低剂量脑灌注CT图像重建方法需要进行反复的投影和反投影运算,计算代价高无法满足实时成像的需求。图像后处理技术因其简单且易于操作已被广泛应用于低剂量脑灌注CT图像恢复。例如,Saito等提出了基于各向异性扩散滤波的低剂量脑灌注CT图像恢复方法;Yu等将标准剂量扫描得到的CT图像进行配准后用于低剂量CT图像滤波;先验图像引导的非局部均值滤波方法极大地降低了目标图像和先验图像在配准精度上的要求;基于先验图像约束的扩散张量滤波方法可以有效解决目标图像和先验图像灰度值不一致产生的误差问题。然而,由于低剂量脑灌注CT图像的噪声非常复杂,使得高精度滤波器的设计非常困难。因此,根据脑灌注CT成像的特点设计出实用的低剂量脑灌注CT图像恢复方法仍是一项具有挑战性的研究课题。
现阶段尚未获得QFR慎用病变的有效临床证据,包括涉及心肌桥的靶病变,Medina分型为1,1,1和1,0,1的分叉病变,升主动脉的冠状动脉开口处3 mm内(不包含3 mm)的病变,造影的狭窄段影像过度重叠、目标血管严重扭曲的病变,仍需要继续收集相关临床数据予以确认。
基于脑灌注CT序列图像的结构相关性,本文提出了一种基于非局部低秩稀疏矩阵分解(NLSMD)的低剂量脑灌注CT图像恢复方法,在有效抑制低剂量脑灌注CT图像噪声和伪影的同时可以较好地保持图像的结构细节特征。
心肌梗死指的是由于心肌缺血时间过长发生坏死,导致心肌功能障碍[6]。诱因多为过劳、突然剧烈运动和环境剧烈变化导致的,也与个人遗传因素有关[7]。心肌梗死后,常常导致室性早搏,临床上也可见心动过速、心脏骤停等,及时治疗下多可恢复[8-9]。
1 方法
1.1 脑灌注CT成像
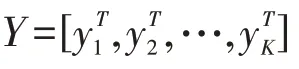

其中,||·||是Frobenious范数,>0 是正则化参数,()是正则化函数。
1.2 低剂量脑灌注CT图像恢复的NLSMD模型
其中,>0 是超参数。
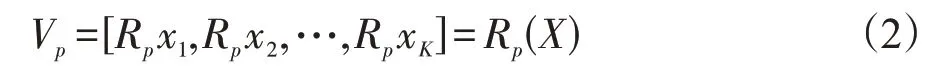
由于这些图像块具有相似的结构,因此其具有低秩特性。
我们可以将矩阵V分解为:V=L+S,其中,L表示低秩矩阵,S表示稀疏矩阵。矩阵L和S可以通过如下问题求出:

其中,||·||是核范数,||·||是ℓ范数,>0 正则化参数,∇表示梯度算子。进一步,公式(3)可以写成如下的无约束优化问题:
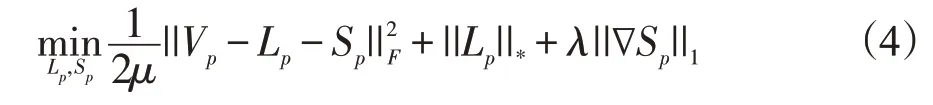
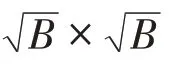
根据Niu 等的体膜实验数据仿真得到50帧大小为256×256 的低剂量脑灌注CT图像数据。相应的成像几何参数为:(1)投影角度为984,每个投影角度的探测元个数为888,每个探测器单元的大小为2 mm;(2)放射源到探测器的距离为949 mm;(3)射线源到旋转中心的距离为541 mm。X 射线的入射光子数目为1×10。
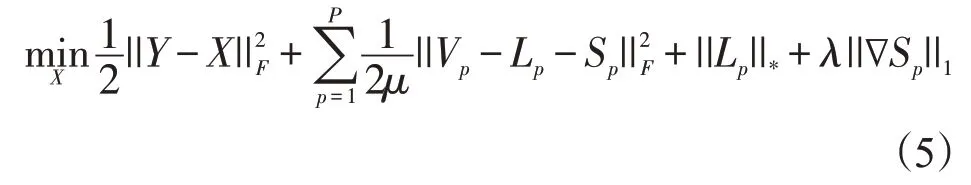
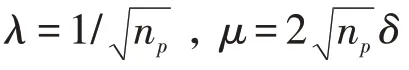
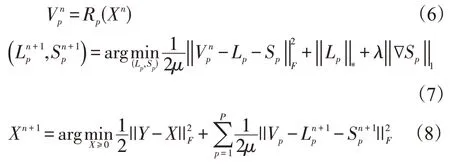
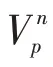
随着HRZ三联抗痨药阳离子脂质体用量的增加(阳离子脂质体质量:siRNA质量=2:1,5:1,10:1,20:1),siRNA包裹效果越好,见图5。
笔者前期通过高通量转录组测序及信息学分析筛选了5种基因(GRP78、NOX1、CEACAM5、HSP60、HDAC1),本研究采用实时定量PCR法在不同血糖状态结直肠癌组织及血液样本中验证上述基因的表达,发现上述基因mRNA表达与结直肠癌患者空腹血糖状态均呈显著正相关,可能与结直肠癌患者的糖代谢异常存在关联。
其中,的迭代格式如下:
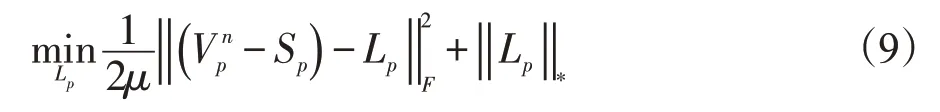
本文利用奇异值分解算法求出式(9)的解:
根据式(16),X可以由下式给出:
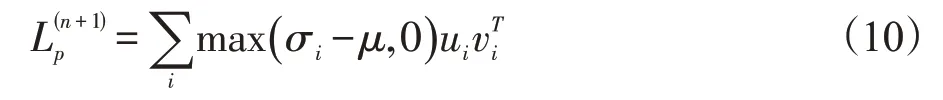
其中,σ,u和v分别是(V-S)的奇异值和特征向量。
固定矩阵L,矩阵S可以由如下问题求解:
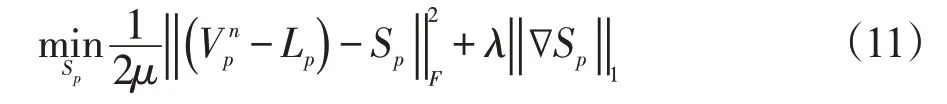
我们使用Chambolle 算法求解式(11),其可以转化为求解如下问题:
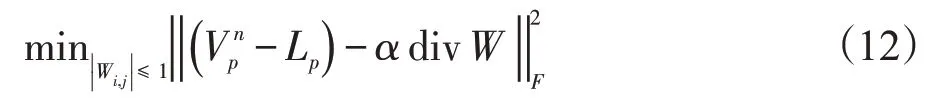
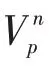
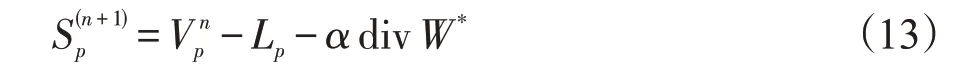
固定矩阵S,矩阵L可以通过下式求解:
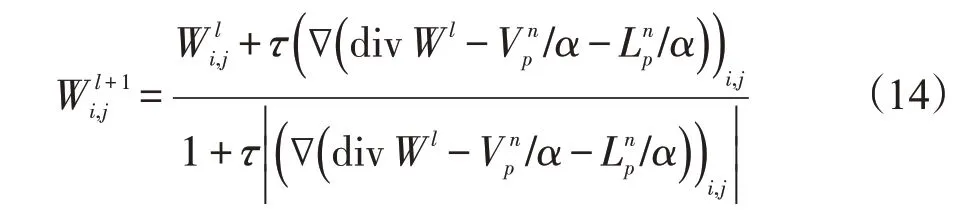
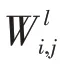
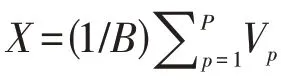
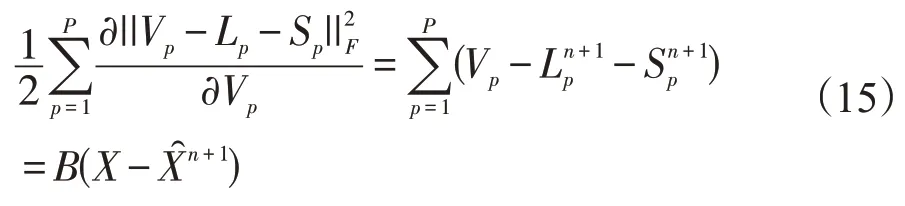
式(15)的解可以由如下的最优性条件给出:

Thus,hyperglycemia induces oxidative stress,which contributes to the accumulation of toxic products,which in turn leads to atherogenic modification of m-LDL,endothelial dysfunction and atherosclerosis progression in patients with diabetes.

综上所述,本文算法的计算步骤如下:
初始化:迭代初始值设置为滤波反投影算法重建的低剂量脑灌注CT图像;
其中,={W}是所有对偶变量W组合而成的矩阵,=,div 是散度算子。若是式(12)的解,则式(12)的解可以由如下公式给出:
日本文学中的“物哀”所包含的“哀伤”“感动”与“无常”经由日本禅宗的洗礼而升华为“寂”,“寂”包含了“幽玄的空寂”和“风雅的闲寂”,后者即芭蕉俳谐艺术的基本美学理念。“风雅者,顺随造化,以四时为友。”“身处不测之风云,劳花鸟之情”〔7〕,人与自然合而为一,领悟并回归无常万象背后永恒的寂灭,珍惜当下,甘于贫困,享受寂寞。其思想基础为物哀,因此不能脱离“无常感”“寂灭感”。
步骤3:根据式(17)更新X;
回国了,在家又过回没有暖气的日子。冰岛虽然连夏天都穿羽绒服,屋里却可以无法无天,穿短袖,吃西瓜,而回到家乡,只能窝在沙发上,裹毯子,喝热水,瑟瑟发抖。作为一个孤陋寡闻的南方人,自从享受了暖气的小确幸,发现再也离不开这项神奇发明。毕竟到了冬天,这条命是暖气给的。
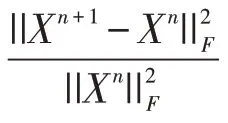
1.3 实验数据
1.2.2 基于NLSMD的低剂量脑灌注CT图像恢复 基于上述方法,我们提出了低剂量脑灌注CT图像恢复的NLSMD模型:
1.4 对比方法
为了验证NLSMD方法的有效性,NLSMD方法分别与滤波反投影(FBP)算法,低秩与稀疏矩阵分解方法(LSMD),低秩与全变分正则化方法(LR-TV)进行了比较。LSMD方法的目标函数为:
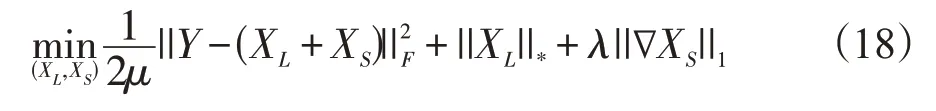
其中,X和X分别为脑灌注CT序列图像的低秩和稀疏部分,>0,>0 为超参数。LR-TV方法的目标函数为:
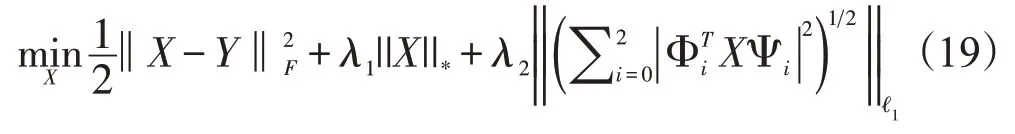
其中,>0,>0 为超参数,Φ=D,Ψ=,Φ=D,Ψ=,Φ=,Ψ=D,是单位矩阵,其中D,D和D分别为沿着,以及方向的差分矩阵。
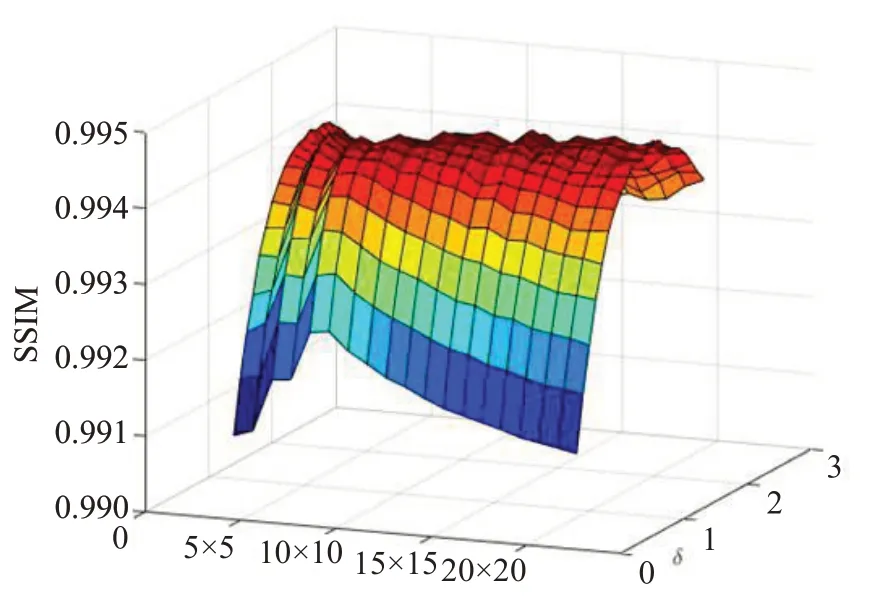
1.5 NLSMD方法的参数选取
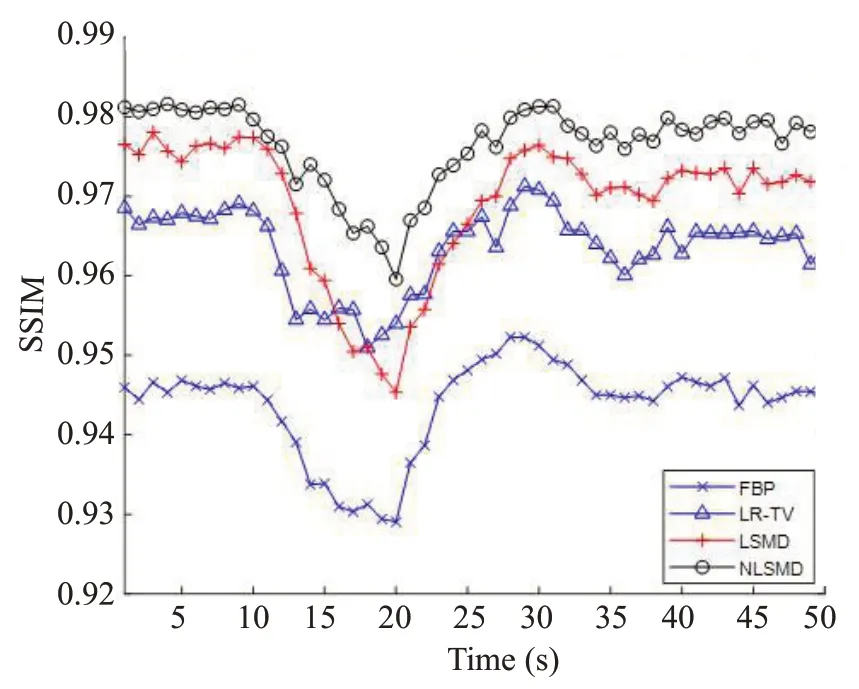
NLSMD方法的参数有图像块的大小n和参数。图1为实验数据中第25帧图像随参数变化时相应的SSIM值图。从图1可以看出,图像块的大小n取15,正则化参数取1.6时,结构相似性(SSIM)值最大为0.9946。
2 结果
2.1 低剂量脑灌注CT图像恢复结果
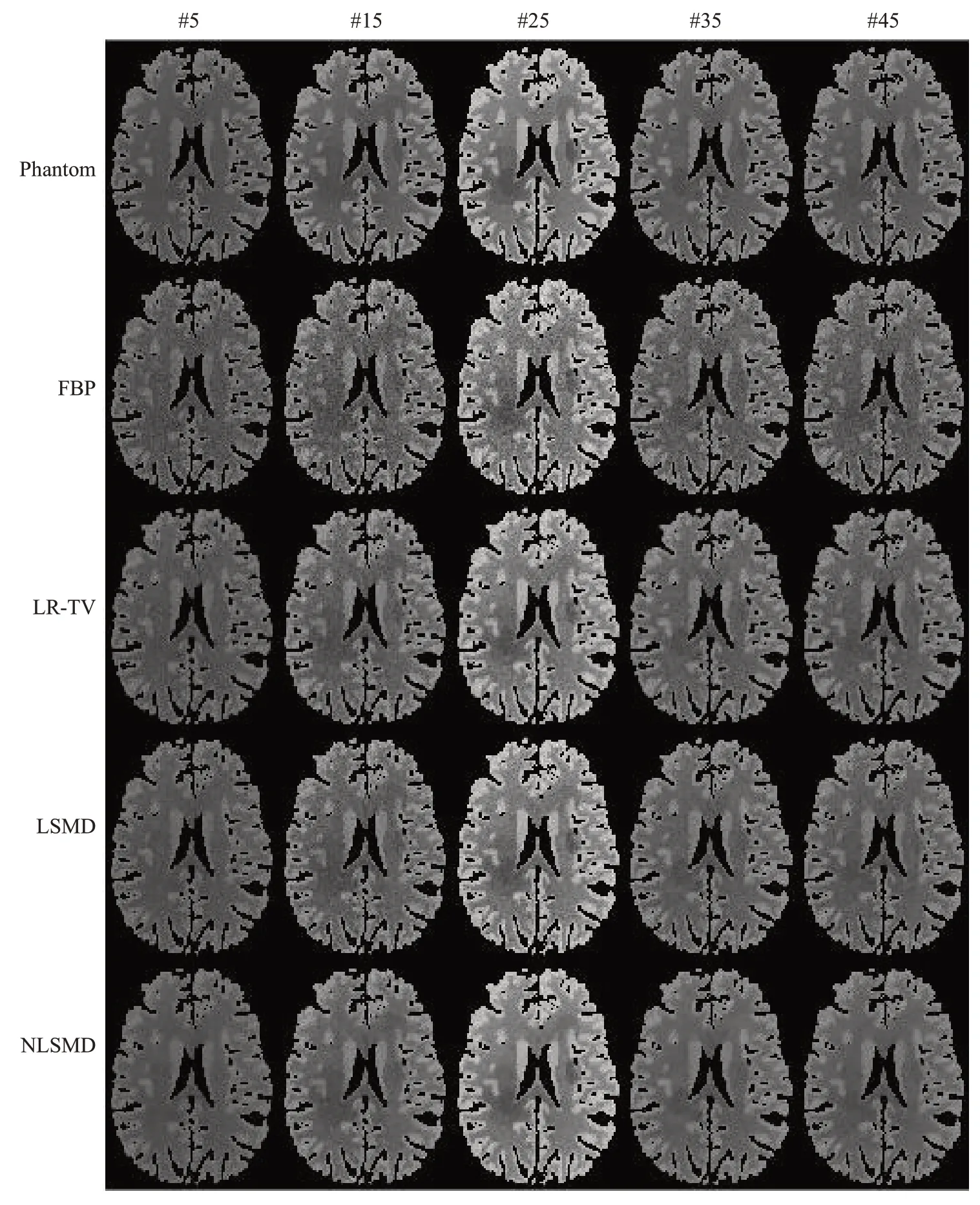
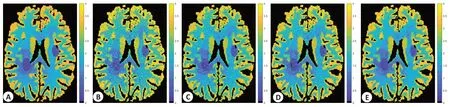
图2给出了低剂量脑灌注CT图像恢复结果。其中,第一行是体膜图像,第二行是FBP图像,第三行是LR-TV方法恢复的图像,第四行是LSMD方法恢复的图像,第五行是NLSMD方法恢复的图像;从左到右第一列为第5帧图像,第二列为第15帧图像,第三列为第25帧图像,第四列为第35帧图像,第五列为第45帧图像。从图2可以看出NLSMD方法的图像与体膜图像最为接近。图3给出了图2中结果的SSIM值。从图3可以看出,FBP方法的平均SSIM值为0.9438,LR-TV方法的平均SSIM 值为0.9636,LSMD 方法的平均SSIM 值为0.9692,NLSMD 方法的平均SSIM 值为0.9765。
近年来,由于中国汽车市场的快速发展,许多领先的汽车制造商在中国加快扩大产能或新建工厂,这为Leadec带来了良好的发展机遇。同时,随着汽车电动化、智能化、网联化和共享化的快速推进,汽车产业发生了新的技术变革浪潮,越来越多的汽车制造商以及零部件制造商愿意选择将工业服务进行外包,从而获得专业高效的服务,提升设备运行的可靠性,提高企业的生产能力和运营效率,将更多的精力集中到市场调研、产品研发、产品质量提升以及生产工艺研究等核心业务上。
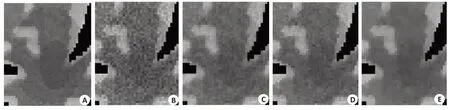
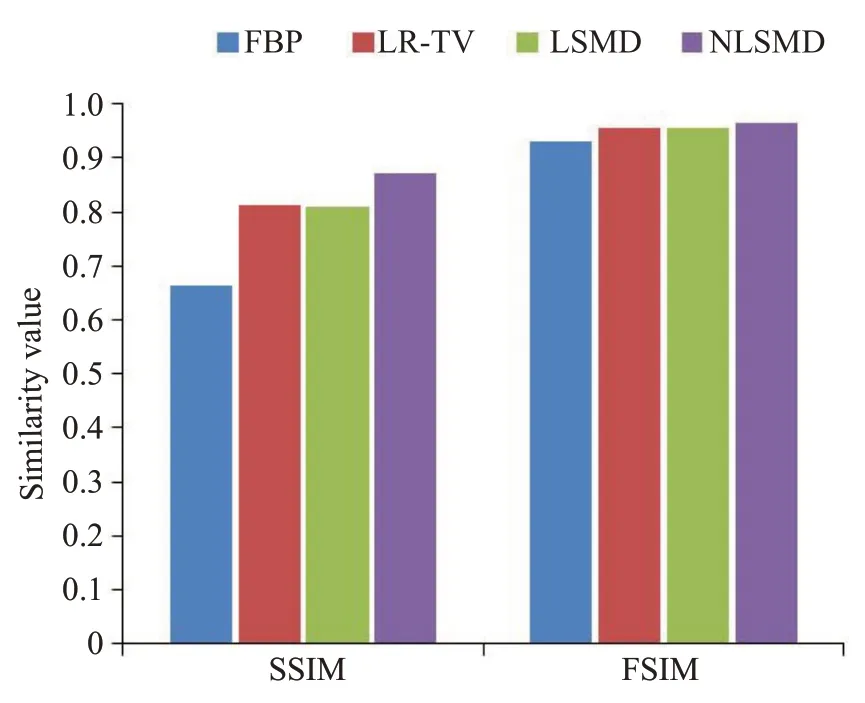
图4为图2中各方法第25帧图像感兴趣区域的局部放大图像。从图4可以看出,NLSMD方法的感兴趣区域的局部放大图像与体膜方法最为接近。为了进一步评价本文方法,我们使用了FSIM值对实验结果进行定量分析。图5为图4的SSIM值和FSIM值。从图5可以看出,FBP方法的SSIM值和FSIM值分别为0.6634和0.9298,LR-TV 方法的SSIM 值和FSIM 值分别为0.813和0.9557,LSMD方法的SSIM值和FSIM值分别为0.8106 和0.9556,NLSMD 方法的SSIM 值和FSIM值分别为0.8727和0.9661。
2.2 脑血流参数图像
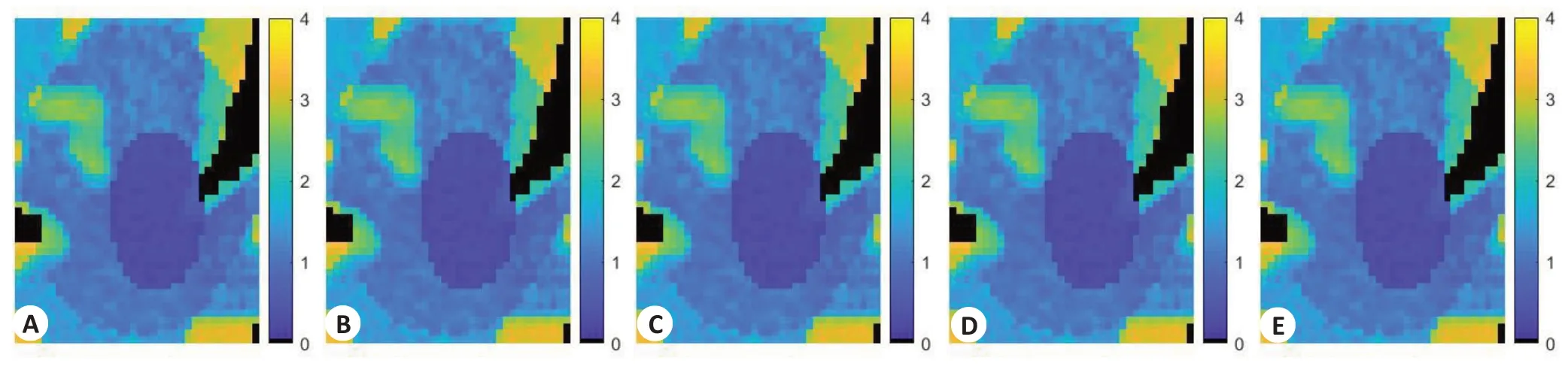
图6为各方法的CBF参数图像,其中图6A为体膜图像的CBF参数图像,图6B为FBP方法的CBF参数图像,图6C 为LR-TV 方法的CBF 参数图像,图6D 为LSMD方法的CBF参数图像,图6E为NLSMD方法的CBF参数图像。图7为图6的SSIM值和FSIM值。从图7可以看出,FBP方法的SSIM值和FSIM值分别为0.7005和0.8748,LR-TV方法的SSIM值和FSIM值分别为0.7736和0.8985,LSMD方法的SSIM值和FSIM值分别为0.7557和0.8940,NLSMD方法的SSIM值和FSIM值分别为0.7871和0.9073。从图6和图7可以看出,NLSMD方法恢复的CBF参数图像与体膜图像的CBF参数图像最为接近。图8为图6感兴趣区域的局部放大图像。图9为图8的SSIM值和FSIM值。从图9可以看出,FBP方法的SSIM值和FSIM值分别为0.6205和0.8321,LR-TV 方法的SSIM 值和FSIM 值分别为0.7485和0.8784,LSMD方法的SSIM值和FSIM值分别为0.7952和0.8935,NLSMD方法的SSIM值和FSIM值分别为0.8540和0.9260。
又因为C为定点,CM为定值,所以,点M的轨迹是以C为圆心,为半径的圆.也就是说,为保持反射光线在水平面内,镜面的法线OM在运动时形成一个以O为顶点的锥面.不过,该锥面并不是我们熟悉的圆锥面(如图2).
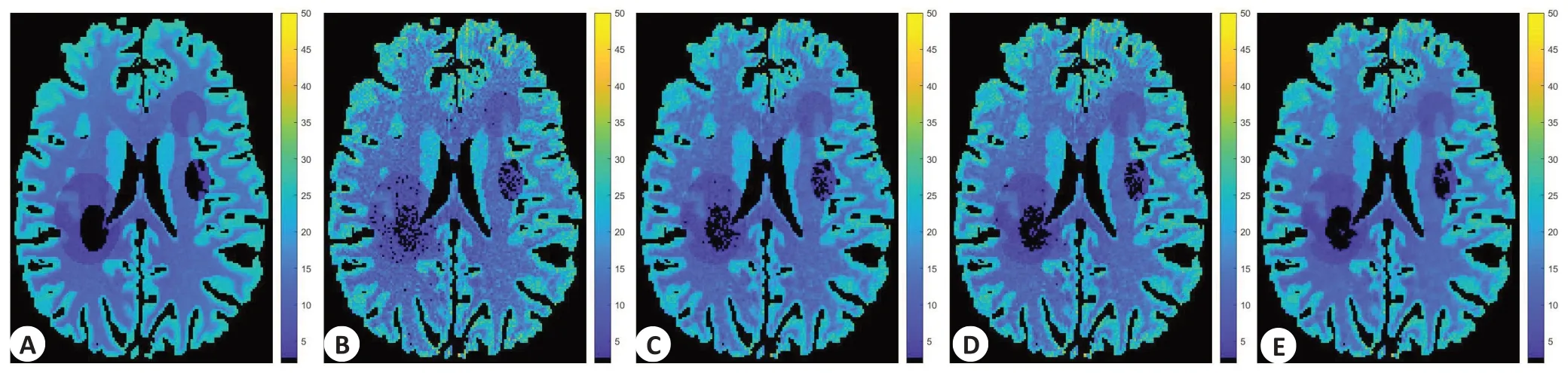
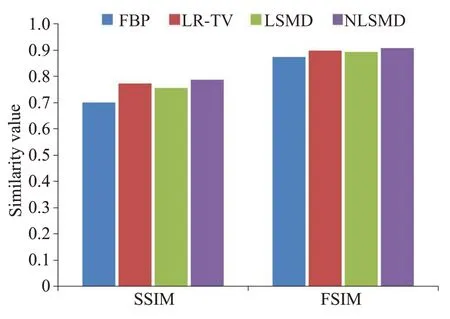
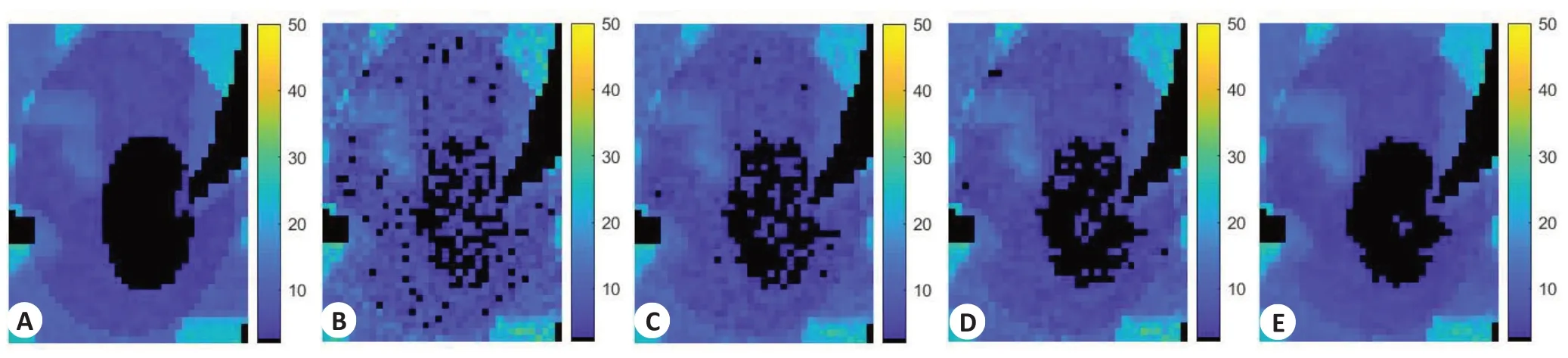
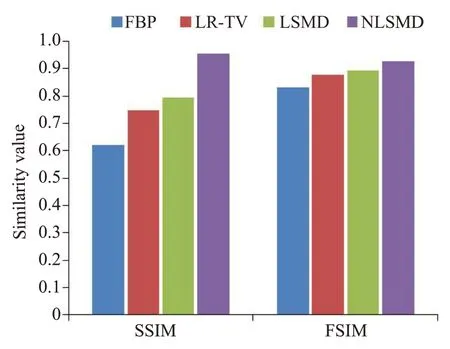
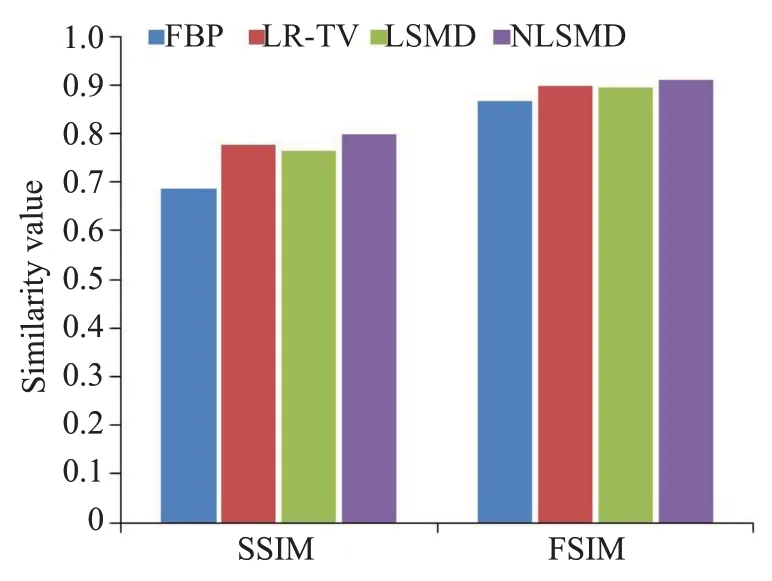
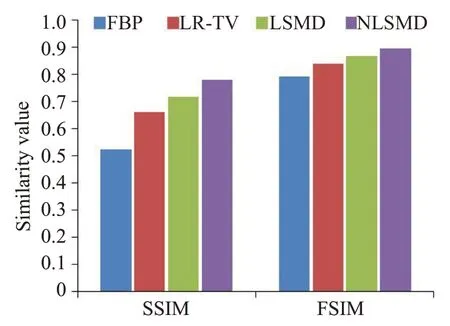
图10为各方法的CBV参数图像,其中图10A为体膜图像的CBV参数图像,图10B为FBP方法的CBV参数图像,图10C为LR-TV方法的CBV参数图像,图10D为LSMD方法的CBV参数图像,图10E为NLSMD方法的CBV参数图像。图11为图10的SSIM值和FSIM值。从图11可以看出,FBP方法的SSIM值和FSIM值分别为0.6856 和0.8657,LR-TV 方法的SSIM 值和FSIM值分别为0.778和0.8966,LSMD方法的SSIM值和FSIM 值分别为0.7642 和0.8949,NLSMD 方法的SSIM值和FSIM值分别为0.7972和0.9110。从图9和图10可以看出,NLSMD方法恢复的CBV参数图像最接近体膜的CBV参数图像。图12为图10感兴趣区域的局部放大图像。图13 为图12 的SSIM 值和FSIM值。从图13可以看出,FBP方法的SSIM值和FSIM值分别为0.5228 和0.7904,LR-TV 方法的SSIM 值和FSIM 值分别为0.6611 和0.8381,LSMD 方法的SSIM值和FSIM值分别为0.7176和0.8664,NLSMD方法的SSIM值和FSIM值分别为0.7800和0.8938。
Bandura的社会学习理论认为,人的侵犯行为倾向由早年学习获得。研究也证实,侵害有时由工作场所的偶然冲突引起,具有侵犯倾向的员工易被激怒而实施侵犯行为,而受害者会被污点化,他们因无法应对这种情境可能会持续受侵害[13]。研究证实遭受伤害的员工可能反过来以各种手段进行还击。研究者将受害者的应对方式分为四类:自我怀疑、消极应对、问题忽略和问题解决等。采取前两种应对方式的受害者会以类似方法对侵害者加以反击[14]。我们推测曾经有过侵犯行为的员工有可能还会实施侵犯行为,而受到过侵犯的员工可能还会受侵犯,或者他们会报复,或者他们会侵犯那些更容易受侵犯的员工。
3 讨论
脑灌注CT成像是脑卒中检查的杰出代表,但脑灌注CT检查的辐射剂量较高,优化控制X射线辐射剂量已成为当前研究的热点问题。目前,低剂量脑灌注CT图像恢复方法利用高质量平扫图像和低剂量脑灌注CT图像之间的结构相似性增强低剂量脑灌注CT 图像质量。但是,先验图像与低剂量图像之间存在差异,会导致恢复结果产生误差。基于脑灌注CT序列图像的结构相关性,本文提出了一种基于非局部低秩稀疏矩阵分解的低剂量脑灌注CT图像恢复方法,该方法利用了低剂量脑灌注CT序列图像自身的结构冗余特性,并对相似的图像块进行非局部低秩稀疏矩阵分解,可以有效地抑制噪声且较好地保持图像细节特征信息。
在数值实验中,NLSMD方法得到的脑灌注CT图像在噪声抑制和细节保持方面有良好的表现。定量实验结果表明,NLSMD方法的平均SSIM值比FBP方法的平均SSIM值提高了3%,与LR-TV方法和LSMD方法相比均提高了1%。进一步,低剂量脑灌注CT图像的感兴趣区域放大图实验结果表明,NLSMD 方法的感兴趣区域放大图的SSIM值比FBP方法提高了31.5%,比LR-TV方法提高了7%,比LSMD方法提高了8%。脑血流动力学参数图像能够精准反映脑组织的灌注情况,为临床诊断和治疗提供重要的参考价值。CBF参数图像的实验结果表明,FBP方法的CBF参数图像存在大量噪声,LR-TV方法与LSMD方法的CBF参数图像的噪声虽然有所抑制,但其与体膜的CBF参数图像仍然存在差距,而NLSMD方法的CBF参数图像与体膜的CBF参数图像最为接近。CBF参数图像的定量结果进一步表明了NLSMD方法的CBF参数图像恢复效果最好。CBV参数图像实验结果表明,NLSMD方法的CBV参数图像无论从整体图像还是感兴趣区域放大图像都与体膜的CBV参数图像最为接近,并且NLSMD方法的CBV参数图像具有最高的SSIM值和FSIM值。综上所述,NLSMD方法恢复的低剂量脑灌注CT图像相比于其他方法恢复效果更好,并且NLSMD方法的CBF参数图像和CBV参数图像与体膜图像的CBF参数图像和CBV参数图像在结构和细节方面也最为接近。
但是,NLSMD方法也还存在一些局限性。首先,NLSMD方法没有考虑噪声统计特性,降低了图像块匹配的鲁棒性。其次,NLSMD方法在实际应用中所需的计算时间也是一个挑战。我们将在未来的研究中将统计噪声建模纳入NLSMD方法中增强NLSMD方法的恢复效果,并且考虑使用多核CPU 和图形处理单元(GPU)硬件来加快NLSMD方法的计算速度。