关于排水砂井未打穿深厚软土地基的固结度计算探讨

陈伟平

(广东粤水电勘测设计有限公司,广东 佛山 528000)

1 概述

广东珠三角地区经常因为存在深厚软土地基需要进行地基处理[1]。预压地基适用于处理淤泥、淤泥质土、冲填土等饱和软黏性土地基。预压处理地基一般分为堆载预压、真空预压和真空～堆载联合预压三类[2]。堆载预压分塑料排水带或砂井地基堆载预压和天然地基堆载预压。一般情况下，当软土层厚度小于4.0 m时，可采用天然地基堆载预压处理。当软土层厚度超过4.0m时，为了加速软土层的固结，通常在拟预压的土层中设置竖向排水体，比如砂井、塑料排水带等竖向排水体[3]。以砂井为竖向排水体、砂垫层为水平向排水体构成系统，在砂垫层的上部堆载作为加压系统的预压法称为砂井堆载预压法。

根据太沙基有效应力原理，在外荷载不变的条件下，随着土体中超静水孔压的消散，有效应力不断增加，土体被压缩，直到达到稳定，这一过程称为固结[4]。从加速土层固结的角度来看，排水砂井如能打穿整个软土层当然是很有利的，但如果软土层很厚，排水砂井要打穿整个压缩土层实际上不太经济，或施工不可能，而且对有的工程也不一定需要[5]。

当排水砂井未打穿深厚软土地基时，地基平均固结度由打了砂井部分土层的平均固结度和砂井以下土层的竖向固结度两部分组成。目前常见计算方法结果显示地基平均固结度与贯入度Q值正相关，一种简明计算方法是根据砂井贯入度值对砂井打穿软土地基时的平均固结度乘以一个小于1的系数来确定。

2 固结度计算

关于排水竖井未打穿深厚软土地基的固结度计算问题，众多学者做了大量的研究工作，但至今还没有得到一个精确又简明实用的固结度计算方法[6]，杨光华[7]认为作为一双层地基来简化计算较为合理。Chen等[8]研究表明，对于竖井处理的深厚软土地基固结度计算问题，竖井下部的固结沉降不可忽略。

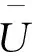
(1)

(2)

式中:

α、β——与排水有关的参数，β值与土的排水距离、固结系数等因素有关，可综合反映土层的固结速率；

下面通过工程实例来计算固结度。

2.1 竖井打穿深厚软土地基

例1：某建筑场地为软土地基，拟采用预压处理地基。根据地质勘察报告，淤泥质土层厚度H=16 m，其下为黏性土层。淤泥质土层竖向和水平向固结系数相同cv=ch=1.5×10-3cm2/s，设计采用砂桩处理，砂桩直径dw=0.3 m，桩长l=16 m，正三角形布置，间距s=1.6 m(如图1所示)。地表设与排水砂井相连的砂垫层，在大面积上覆堆载作用下，试计算：地基在90 d时的竖向、径向固结度和平均固结度(不考虑井阻和涂抹影响)。

图1 地基处理断面及平面示意(单位：mm)

解：设置了排水砂井后，固结度以径向固结为主，竖向固结度较小。

1) 相关参数

有效排水半径de=1.05 s=1.05×1.6=1.68 m。

单面排水，H=16 m。

平均：βrz=βz+βr=1.249×10-4+0.035 4=0.035 55/d。

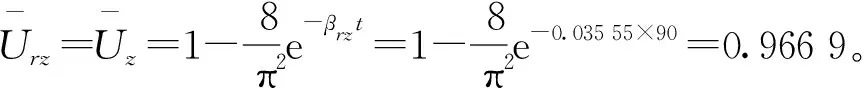
2.2 竖井未打穿深厚软土地基

当排水竖井未穿透受压土层时，现行建筑地基处理技术规范[2]未明确规定固结度的计算方法，只是笼统地规定“竖井范围内土层的平均固结度和竖井底面以下受压土层的平均固结度，以及通过预压完成的变形量均应满足设计要求”。

图2 砂井未打穿软土层的情况示意

整个压缩土层的平均固结度按下式计算：

(3)

式中:

(4)

式中:

A1——竖井部分土层起始孔隙水压力分布曲线所包围的面积(取附加应力σz分布曲线包围的面积)；

A2——竖井以下土层起始孔隙水压力分布曲线包围的面积(取σz分布曲线包围的面积)。

假定起始孔隙水压力不随深度而变化，则贯入度Q可简化为[10]：

(5)

式中:

H1——竖井部分土层厚度；

H2——竖井以下压缩层范围内土层厚度。

对于竖井未穿透软土层的地基，当竖井底面以下软土层较厚时，竖井范围土层平均固结度与竖井底面以下土层的平均固结度相差较大，预压期间所完成的固结变形量也因之相差较大，若将固结度按整个受压土层平均，则与实际固结度沿深度的分布不符，且掩盖了竖井底面以下土层固结缓慢，预压期间完成的固结变形量小，建筑物使用以后剩余沉降持续时间长等实际情况。同时，按整个受压土层平均，使竖井范围土层固结度比实际降低而影响稳定分析结果。因此，竖井范围与竖井以下土层的固结度和相应的固结变形应分别计算，不宜按整个受压土层平均计算。

1) 常规法

2) Hart法

3) 谢康和改进法

H′=(1-aQ)H

碧流河水库配有主空气压缩机2台，其中一台作为备用；副空气压缩机1台，其工作状态为间歇式，即在主空气压缩机停止输气时，由副空气压缩机（气泵）向管内补充气压，使系统内气压保持在0.01～0.05 MPa之间，确保管路系统始终处于有压状态，以防止管内产生冰阻现象。还需设置储气罐1个，起到缓冲气压作用；气液分离器1个，起到净化空气作用。

(6)

下面通过工程实例来计算固结度。

例2：若砂井长度为H1=10 m，未打穿淤泥质土层，H2=6 m，其余条件同例1(如图3所示)。试计算：地基在90 d时的竖向、径向固结度和平均固结度。

图3 砂井未打穿软土层示意(单位：mm)

解法1：常规法

取竖井的长度作为竖向排水距离，砂桩长度为10 m，土层单面排水，取H=H1=10 m。

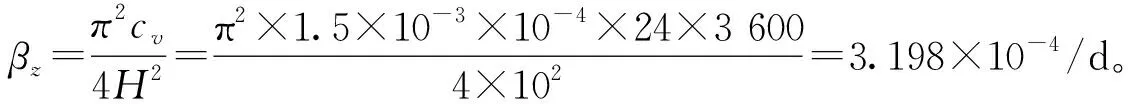
平均：βrz=βz+βr=3.198×10-4+0.035 42=0.035 74/d。

取竖井底面为排水面，按单向固结理论计算，H=H2=6 m。

解法3：H′=(1-aQ)H

排水距离H′=(1-aQ)H，βz和βrz例1相同，即βz=1.249×10-4/d，βrz=0.035 55/d。

H′=(1-aQ)H=(1-0.941×0.625)×16=6.59 m。

表2 砂井打穿软土层平均固结度计算成果

表1 砂井未打穿软土层平均固结度3种解法计算成果对比

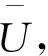
图4 砂井贯入度Q与关系示意

由图4可见，3种方法计算结果接近，常规法最大，谢康和法次之，Hart法最小；随着贯入度的增加，计算结果差距同步增大，但总的来说相差不大；3种方法计算结果基本上与贯入度Q值正相关。当贯入度Q≥0.9时，常规法与谢康和法在尾部有个平缓段，说明此后再增加砂井深度对提高地基平均固结度帮助不大。3种计算方法结果表明，地基平均固结度均与贯入度正相关，Hart法正相关性最好，谢康和法次之，常规法又次之。由图4可见，当Q=0.95时，常规法计算的固结度比砂井打穿软土地基时的固结度还大，这显然是不合理的，对此谢康和法对常规法作了优化。相对而言Hart法比较合理。

ψ=aQ+b

(7)

式中:

a——直线斜率，与地基参数和砂井设计参数有关；

b——直线截距，为不打砂井时的地基平均固结度与砂井完全打穿时的固结度之比。

就本例而言，若采用Hart法计算，则ψ=0.7947Q+0.2053，当Q=0时，ψ=0.2053；当Q=1.0时，ψ=1.0；当0

从保守角度考虑，一般工程建议采用Hart法的计算软土地基的平均固结度。

3 结语

一般而言，不考虑井阻和涂抹影响，当砂井未打穿深厚软土地基时，目前常见的3种方法计算结果接近，常规法最大，谢康和法次之，Hart法最小；随着贯入度的增加，其计算结果相差程度同步增大，但总的来说相差不是很大，3种方法计算结果表明地基平均固结度与贯入度值正相关。当砂井未打穿深厚软土地基时，地基平均固结度的一种简明计算方法是根据砂井贯入度Q值对砂井打穿软土地基时的平均固结度乘以一个小于1的系数ψ来确定，ψ与Q呈线性关系，当Q=0时，ψ为不打砂井时的地基平均固结度与砂井完全打穿时的固结度之比，当Q=1.0时，ψ=1.0；当0

相对而言，Hart法比较合理，一般工程建议采用Hart法的计算软土地基的平均固结度。

不同地区土的特性、土工参数对计算结果影响较大。目前仍需积累工程经验，改进砂井未打穿深厚软土地基时地基平均固结度计算方法，以期达到理论计算与实测结果大致相符、安全性和经济性兼顾的设计目标。