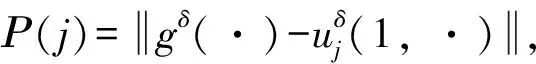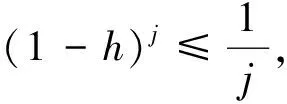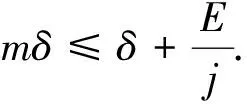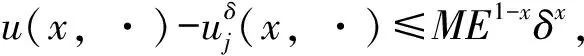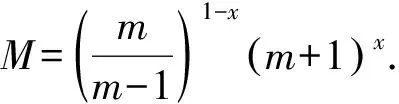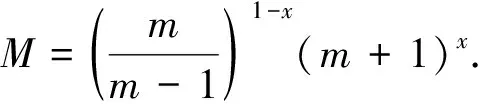含对流项逆热传导问题的迭代正则化方法
赵 齐,程 炜
(河南工业大学 理学院,河南 郑州 450001)
1 引言
众所周知,在许多工程应用中,需要由物体内部的某处固定位置的温度测量值来反演表面的温度或者热流[2-4],这就是逆热传导问题(IHCP)[5].该类问题是严重不适定的,即微小的数据波动将会引起解的巨大误差,以致解的爆破,使其数值计算和理论分析都非常困难.在这种情况下,需要通过一种正则化技术来保证这类问题的解对数据的连续依赖性[6].关于逆热传导问题已经建立了许多正则化方法,例如中心差分正则化方法[7-8]、Fourier方法[9-10]、拟逆方法[11-12]、小波方法[13-14]等.据我们所知,目前很多学者的文献都是关于标准的一维逆热传导问题,对于非标准的一维逆热传导问题的研究相对较少.
本文考虑如下含对流项的逆热传导问题[15-16]:
(1.1)
该问题需要从已知数据g(t)来反演0 我们考虑问题在L2()下的变量t,u(x, ·),g(·)=u(1, ·),f(·)=u(0, ·)和其他函数在t<0时,其函数值为零.这里表示L2()中范数,δ>0是测量误差,用g和gδ表示u(x,t)在x=1时的精准值和测量值,并满足: (1.2) 假设对f(·):=u(0, ·)存在如下先验界: (1.3) 其中 (1.4) 函数f(t)的 Fourier 变换为 本文对变量t做Fourier变换得到问题(1.1)的解: (1.5) 其中 ξ∈, τ=sign(ξ). 在本节中,我们考虑问题(1.1)在条件(1.3)下的条件稳定性估计. 定理2.1函数u(x,t)和g(t)分别是问题(1.1)的精准值和实际测量值,u(0,t)满足(1.3)式,当x∈(0, 1)时,有以下估计: (2.1) 证明由Parseval等式和Hölder不等式以及(1.5),得到 此外,有以下不等式成立 (2.2) 所以,在先验界条件(1.3)和(2.2)下,得 即证得定理2.1. 推论2.1函数u1(x,t),u2(x,t)和函数g1(t),g2(t)分别是问题(1.1)的精准解和近似解,当x∈(0, 1)时,有以下估计成立 (2.3) 然而,条件稳定性的结果不能保证含噪声数值计算的稳定性.因此,需要有效的正则化方法来解决问题(1.1),并恢复解的稳定性. 在本部分,我们采用一种修改的迭代正则化方法来处理问题(1.1),并且构造出问题的正则近似解;在一种先验和一种后验参数选取规则下,分别获得了问题(1.1)的Hölder 型误差估计. 设Κ:X→Y是具有紧性的线性算子, x=(Ι-aK*K)x+aK*y, (3.1) 并用迭代法解此方程,设迭代步数为m,即 x0=0,xm=(Ι-aK*K)xm-1+aK*y, m=1, 2, 3, … (3.2) 其中0 (3.3) 引理3.1当0≤h≤1,0≤β≤1和n≥1时,得 (3.4) (3.5) 证明令f(h)=(1-h)nhβ,0≤h≤1,则有 f′(h)=-n(1-h)n-1hβ+β(1-h)nhβ-1 =(1-h)n-1hβ-1[-nh+β(1-h)]. 此时, f″(h)=-n[-(n-1)(1-h)n-2hβ+ β(1-h)n-1hβ-1]+β[-n(1-h)n-1hβ-1+ 即得到结果(3.4),类似可证得(3.5). 证明由Parseval等式,(1.5)和(3.2),得 e(1-x)θ(ξ)|δ≤(1-h)jhxE+[1-(1-h)j]h(x-1)δ ≤2E1-xδx. 以上是我们通过迭代的正则化方法得到Hölder 型误差估计,表明了该方法处理这类逆热传导问题的不适定性是有效的. 在本节中,我们将考虑在迭代正则化方法(3.2)下的Morozov停止规则: (3.6) 其中m>1为常数,j是正则化参数. 为了建立式子(3.6)的解的存在性,我们有以下引理成立: (a)Ρ(j)是连续函数; 引理3.3有以下式子成立 (3.7) 证明由Parseval等式和(3.6)得 所以有 即证得引理3.3. (3.8) 证明由Parseval等式、三角不等式、(1.2)、(3.6)、(3.7)和h=|e-θ(ξ)|,我们得到 (3.9) 和 (3.10) 由Parseval等式、(3.9)和(3.10)可得 即证得定理3.2. 本文通过两种参数选取规则,都得到了正则解与精确解之间的Hölder 型误差估计,由于在实际中问题的精确解不容易获得,所以无法得到先验解,但是后验参数的选择克服了这一点.因此,后验参数选择使得计算更方便.


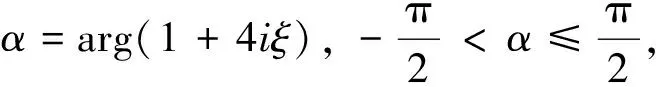

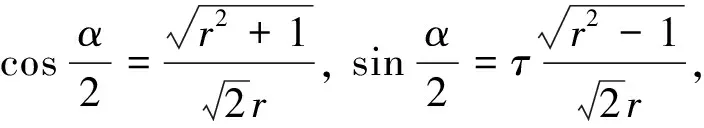
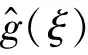
2 条件稳定性


3 正则化方法和误差估计
3.1 正则化方法
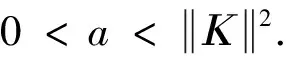


3.2 先验参数选择下的误差估计
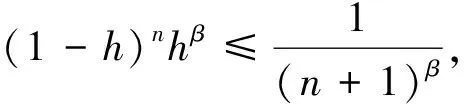
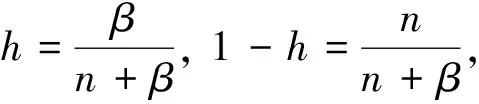
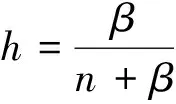
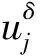

3.3 后验参数选择下的误差估计