ECWMF高分辨率模式2 m温度预报在六盘水市的误差分析及订正指标

夏 阳，孙 翔，胡 萍，张 强，陈翱章，王 芬

(1.贵州省六盘水市气象局，贵州 六盘水 553000；2.贵州省铜仁市气象局，贵州 铜仁 554300；3.贵州省黔西南布依族苗族自治州气象局，贵州 兴义 562400)

0 引言

近年来，气象事业在保障国民经济发展和服务社会公众生活中的地位不断提升，地方政府部门和社会公众对于更加全面、准确、精细的天气预报信息需求也愈加旺盛。由于数值模式的预报偏差在较长的一个时期内始终存在[1]，想要获取高时空分辨率和高准确率的预报信息，除了通过优化初值场和物理过程参数化方案提升高分辨率数值模式的预报能力外，加强对数值模式产品的客观化分析和解释应用也是提升精细化预报准确率的重要途径[2]。

温度是天气预报中最为重要的气象要素之一。目前，国内气象工作者对温度的模式预报误差订正开展了众多研究，通过线性回归[3]、滑动平均订正[4-5]、统计降尺度[6-7]和卡尔曼滤波法[8-9]等诸多方法能够显著降低模式的预报误差，提升模式的预报效果，但在一定程度上存在建模样本量较少、不适应转折性天气变化、缺少应用检验等问题[10-11]。

尽管数值模式的预报能力不断提升，亦有部分气象工作者对数值模式在贵州各地的预报订正方法进行了初步研究[12-13]，但EC高分辨率模式在六盘水市的温度预报误差及其与实际的温度预报准确率之间的差距仍然存在。目前当地的温度预报主要依靠业务人员的主观经验来对数值模式预报结果进行订正，但此种方法主观因素多、效果不稳定，而且预报技能的掌握和积累周期较长，使得温度预报水平的提升受到很大限制。因此有必要对EC高分辨率模式在六盘水市的温度预报误差和订正指标进行研究和总结，将主观经验客观化、指标化，为今后客观预报方法中温度预报的发展提供思路。

1 资料与方法

1.1 资料

欧洲中期天气预报中心(ECWMF，以下简称EC)高分辨率预报模式中的2 m温度产品，起报时间分别为每日的08时和20时(北京时间，下同)，空间分辨率为0.125 °×0.125 °，时间分辨率在72 h预报时效内为3 h，72～240 h预报时效为6 h。六盘水市3个国家气象观测站(水城、盘州、六枝)的逐日观测资料，要素包括最高气温、最低气温、平均相对湿度和日照时数等。文中的逐日资料均为20—20时。

研究时段为2018年1月1日—2020年11月30日。其中，2018年1月1日—2019年12月31日为预报误差及订正指标的统计分析时段，共730 d；2019年12月1日—2020年11月30日为检验时段，共366 d。

1.2 方法

本文采用双线性插值、标准差分析、概率分布统计等常规气候统计方法对20—20时的逐日站点温度(最高和最低)预报和实况进行分析。文中有关名词定义如下：

温度预报值：利用双线性插值方法，将各时效的2 m温度预报产品插值到六盘水市3个国家气象观测站上，分别得到3个站点的温度预报值。针对某一日的最高温度与最低温度预报值，将对应时段的所有时次温度预报值中的最大值作为最高温度预报值，最小值作为最低温度预报值。

预报时效：针对某一日(T)20—20时的温度预报，前期第1～6 d(T-1～T-6)08时起报所对应的预报时效分别为12～36 h、36～60 h、36～60 h、84～108 h、108～132 h、132～156 h，前期第1～6 d 20时起报所对应的预报时效分别为0～24 h、24～48 h、48～72 h、72～96 h、96～120 h、120～144 h。

未来5 d预报：根据目前日常预报业务中的工作流程，对某一日(T)所制作的未来5 d(T+1～T+5)的模式温度预报进行如下定义(表1)。

将前期第0～5 d 08时起报的12～36 h、36～60 h、36～60 h、84～108 h、108～132 h、132～156 h预报时效以及前期第1～5 d 20时起报的24～48 h、48～72 h、72～96 h、96～120 h、120～144 h预报时效内共11个温度预报值进行算术平均，得到的结果作为未来第1 d的模式温度预报(即为未来24 h预报)。同理，分别得到未来第2～5 d(未来48～120 h预报)的模式温度预报。

5 d综合：根据《贵州省中短期天气预报质量检验办法》，按照第1 d至第5 d的预报准确率分别按照10/27、8/27、6/27、2/27、1/27的权重进行加权平均计算后，所得结果即为5 d综合预报准确率。

表1 当前日期(T)所制作的未来5 d预报所对应的不同起报日期及预报时效(单位：h)Tab.1 different start date and forecast time corresponding to the forecast for the next 5 days(unit:h)

预报误差：温度实况减去预报值所得到的差值，称为预报误差，单位为℃。

误差占比：根据温度预报的业务考核标准，当预报误差处于±2 ℃之间时均算作预报正确。此时，选取1个预报误差e，统计在2018年1月1日—2019年12月31日共730 d的时段中，误差范围处于[e-2 ℃,e+2 ℃]之间的频次及其占全部时段的百分比，称为该误差的占比，单位为%。当占比取得最大值时，将该误差e称为最大占比误差。

2 不同预报时效的模式温度预报误差分析

2.1 预报误差及标准差的年均分布

图1为六盘水市3个国家气象观测站不同预报时效的模式预报误差年均分布。由图1a可见，各站点的最低温度年平均预报误差均在1.5 ℃以下，并且与固有认知不同，最低温度预报误差呈现随时效的增加而逐渐减小的现象。其中水城和六枝20时起报的0～24 h最低温度较08时起报的12～36 h存在小幅的跃增，幅度在0.2～0.3 ℃。除0～24 h之外，对0～84 h和72～156 h预报时效的平均误差进行统计发现，由于前者的时间分辨率较高，导致前者的最低温度预报误差明显大于后者。

图1 不同预报时效的年平均误差(a,最低温度; b,最高温度)Fig.1 Annual average bias of different prediction aging (a,minimum temperature; b,maximum temperature)

对于最高温度(图1b)，水城和六枝的模式预报误差同样存在随时效的增加而逐渐减小的情况，但变化幅度要略小于最低温度。相对来说，盘州不同时效的最高温度预报误差更为稳定，处于2.3～2.5 ℃之间。同时由于最高温度往往仅与14时温度密切相关，使得在前后两段预报时效(0～84 h和72～156 h)上，预报误差并不存在最低温度那样的显著差异。总体来看，水城、盘州、六枝3个站各时效平均的最高温度年均预报误差分别达到了1.7 ℃、2.4 ℃、0.9 ℃，要高于最低温度的0.7 ℃、1.0 ℃、0.7 ℃。

在预报误差标准差的年均分布(图2)方面，各个站点均遵循了预报时效越长、波动越大的特点和规律。但3个站点各个时效的最低温度预报误差标准差(图2a)均低于1.8 ℃，甚至低于最高温度(图2b)中的0～24 h时效(2.2 ℃)，表现出较好的稳定性。相比之下，最高温度的误差标准差普遍超过了2.5 ℃，在96～120 h时效后甚至超过3 ℃，表明了数值模式对于最高温度预报较最低温度存在更大的不确定性，尤其是在更长时效上。

图2 不同预报时效的年平均误差标准差(a,最低温度; b,最高温度)Fig.2 Standard deviation of annual average bias of different prediction aging (a,minimum temperature; b,maximum temperature)

2.2 预报误差及标准差的年变化

图3为各个站点不同预报时效预报误差的年变化分布，对于最低温度(图3a、3c、3e)，除了六枝(图3e)在2月份超过60 h预报时效的时段内出现预报误差为负值的情况，其余月份和站点的在不同时效内的预报误差均处于0～1.8 ℃之间。月分布显示，水城、六枝(图3a、3e)在1月和2月的预报误差最小，普遍低于0.5 ℃，春季(3—4月)和盛夏(7—8月)相对较大，而盘州(图3c)除晚秋—初冬(11—12月)预报误差相对较低(接近0.5 ℃)外，其余月份的预报误差普遍在1 ℃以上。

对于最高温度(图3b、3d、3f)而言，年内各个月的预报误差分布型与最低温度相似，但变化幅度有明显增大，其中，水城、六枝(图3b、3f)呈明显的双峰型分布，预报误差在春季(3—4月)和盛夏(7—8月)为波峰，误差值普遍超过2 ℃，其中春季是热低压系统的高发期，从而使得处于热低压控制下的黔西地区时常出现晴朗少云天气，最高温度往往较模式预报温度明显偏高；而在冬半年(10月—次年2月)以及春末初夏(5—6月)为波谷，误差值低于1 ℃，其中六枝在10月和1—2月甚至达到负值，接近-1 ℃，这是由于冬半年云贵准静止锋活跃，处于锋后的水城和六枝最高温度低于模式预报温度。相比之下，处于静止锋前的盘州(图3d)的最高温度预报误差波动呈多峰谷分布，变化幅度较水城、六枝小，其中8月最大，可达3.7 ℃，10月最小，为1.4 ℃，其余月份处于2～3 ℃之间。

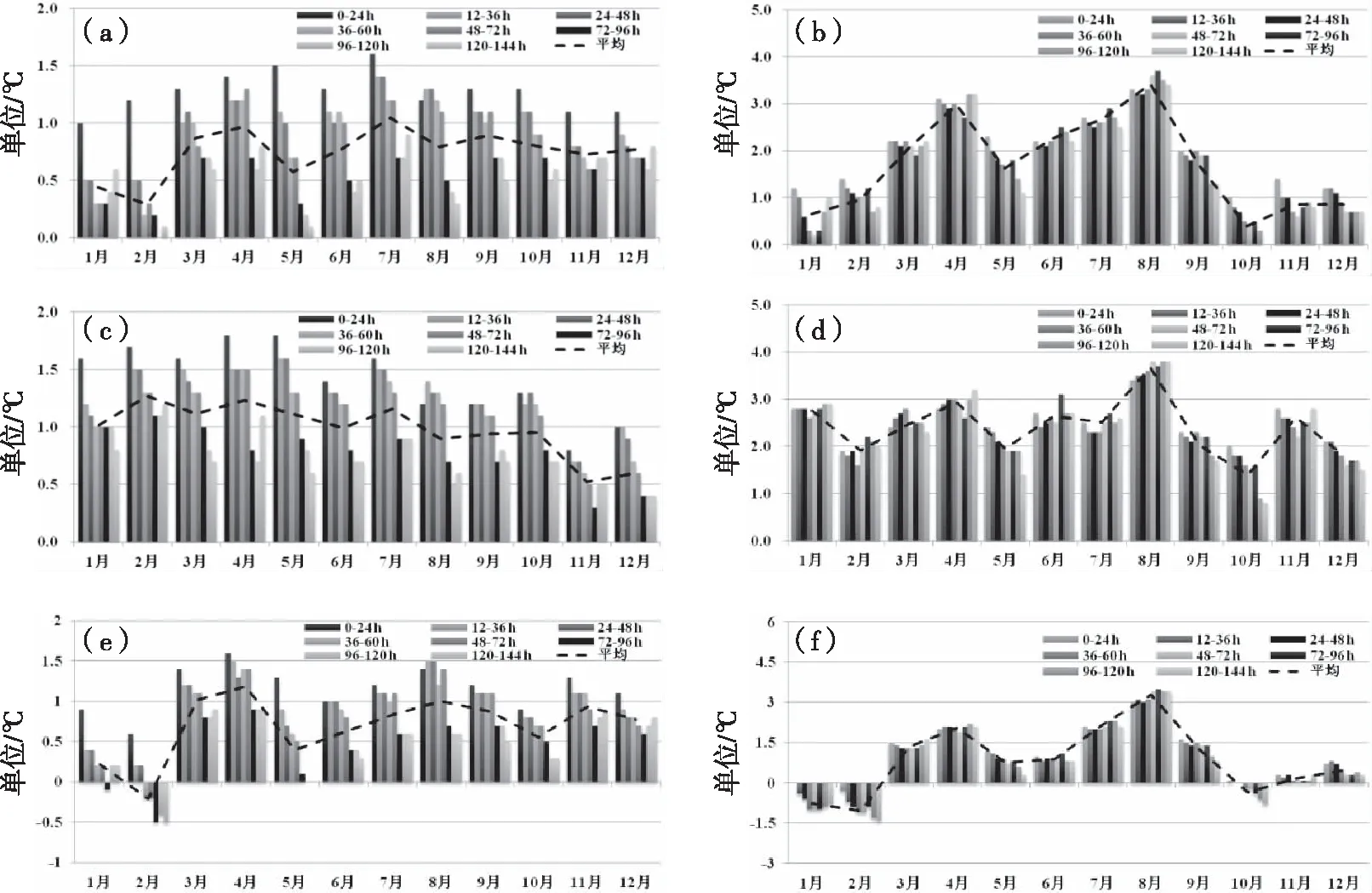
图3 不同预报时效的预报误差年变化(a,b为水城，c,d 为盘州，e,f为六枝；a,c,e为最低温度; b,d,f为最高温度)Fig.3 Annual variation of prediction bias for different prediction aging (a and b are Shuicheng,c and d are Panzhou,e and f are Liuzhi；a,c and e are minimun temperature; b,d and f are maximun temperature)

针对各个站点在不同预报时效的预报误差标准差年变化分析(图略)可知，无论是最低温度还是最高温度，在年内的标准差变化均呈单峰(谷)型分布，夏季(6—8月)的标准差明显低于其余月份，3个站的最低温度预报误差标准差均接近1 ℃左右，最高温度的预报误差标准差降至2 ℃以下。而冬季(12月—次年2月)的标准差最大，水城、盘州、六枝各个时效平均的最低温度预报误差标准差最大分别可达到2.0 ℃、2.4 ℃、1.6 ℃，最高温度误差标准差甚至超过3.5 ℃。

因此，对于六盘水而言，从综合预报误差及其标准差的年变化来看，模式的温度预报在初夏(6月)可靠性最高，而在春季(3—4月)可靠性最低。

3 未来5 d预报的预报误差统计

由前文的分析可知，由于模式预报对于单个时效的预报存在较大误差和不确定性，其预报准确率远远不能满足预报业务需求，且由于目前相关业务规定,对温度预报质量的考核时段为5 d(120 h)。因此，本文将采用如表1所示的方法，将多时效对于同1 d的预报值进行算术平均，从而获得模式对于未来5 d(未来24 h、48 h、72 h、96 h、120 h)多时效平均的温度预报值，并通过对2018年1月1日—2019年12月31日共730 d内不同预报天数的预报误差及其占比进行统计，选取最大占比误差作为预报值的订正指标。

3.1 年平均预报误差

表2给出了模式对于未来5 d(24～120 h)预报的年平均预报误差值。由表可见，经过多时效预报平均后，模式对于未来5 d(24～120 h)的平均误差相比原本的单时效(图1)更加稳定，将全市3个站点的最低温度以及六枝的最高温度预报误差限制在了1 ℃以下，且预报误差随预报时效的变化幅度低于0.2 ℃。除此之外，水城和盘州的最高温度平均预报误差也分别在1.6～1.7 ℃和2.3～2.4 ℃之间。

表2 未来5 d(24～120 h)预报的年平均预报误差(单位：℃)Tab.2 Annual average forecast bias of forecast in the next five days (24～120 h，unit：℃)

在初步了解模式对未来5 d(24～120 h)的平均预报误差之后，我们仍然关心不同的预报误差e及其e±2 ℃范围内的误差值在过去2 a(2018—2019年)中所出现的频次及占比，尤其是能够达到最大占比的预报误差e。

全市3站不同预报天数的预报误差最大占比统计结果如表3所示。当水城未来24 h最低温度预报误差值(实况-预报)e=1.0 ℃时，处于e±2 ℃(-1～3 ℃)范围内的预报误差值共占到了90.14%，对此我们即可理解为：倘若在过去2 a的730 d中，对于水城未来24 h的模式最低温度预报值进行+1 ℃的订正之后，预报准确率可以达到90.14%。同样，水城站未来48～120 h的预报准确率分别可达到89.04%、87.81%、85.48%、83.29%，据此所得5 d综合最低温度预报准确率为88.70%。

表3 未来5 d(24～120 h)预报误差最大占比统计分布Tab.3 Statistical distribution of the largest proportion of prediction error in the next five days (24～120 h)

在对水城的最高温度以及盘州、六枝的温度预报误差进行同样的统计后，若全部根据相应的最大占比误差直接进行订正，那过去2 a的六盘水市5 d(120 h)综合最低温度预报准确率将达到88.11%，最高温度预报准确率可达到62.29%，温度预报准确率为75.20%。但上述预报准确率除了与气象事业现代化发展要求和社会公众需求之间存在较大差距外，还远低于六盘水市2018年(82.87%)和2019年(79.36%)的实际温度预报准确率，因此有必要进一步分析。

3.2 月平均预报误差

对逐月的预报误差最大占比统计结果再次进行统计(图略)，并采用逐月的最大占比误差作为指标对3个站点的模式预报值进行订正，得到的5 d(120 h)温度预报准确率如表4所示。由表可知，此时最低温度预报准确率提升至89.90%，较采用年平均最大占比误差进行订正的预报准确率(88.11%)提升了1.79%，而最高温度的平均预报准确率则有大幅度的提升，达到69.82%，较年平均订正提升了7.53%，其中六枝最高温度预报准确率提升幅度甚至超过了10%，而综合温度预报准确率达到79.86%，较之前提升了4.66%，已超过2019年六盘水市的实际预报准确率。表明基于气候概率统计得到的逐月指标订正方法能够明显提高数值模式对六盘水市的温度预报能力，在一定程度上为提升预报质量提供了较大的可能性。

表4 通过逐月指标订正得到的全市120 h温度预报准确率及较年平均订正的涨幅Tab.4 Accuracy of 120 h temperature forecast through monthly index correction and increase compared with the annual average correction

4 不同天气背景下的未来24 h最高温度预报误差

由表4可知，逐月指标订正方法对于提升六盘水市预报质量的潜在作用已经呈现， 120 h最低温度的平均预报准确率接近90%，已达到近年来预报准确率的前列，且进一步提升的幅度已相对有限。相比之下，逐月指标订正所得到的最高温度平均预报准确率低于70%，仍有较大的提升空间。由于最高温度的预报误差受天气系统和天空状况的影响程度远大于最低温度，本文还对不同天气背景下模式的最高温度预报误差和站点日较差进行了统计。利用站点观测的气象要素实况资料，根据不同的日照时间和平均相对湿度条件，将天气类型定义为晴天、阴天、雨天3类。日照时间 ≥2 h定义为晴天，0<日照时间<2 h 或日照时间=0 h且平均相对湿度<80%定义为阴天，日照时间=0 h，且平均相对湿度≥80%定义为雨天。

此外，考虑到模式对于较长时效天空状况的预报仍然具有较大的不确定性，因此，本文仅根据不同的天气类型对模式的未来24 h最高温度预报误差和日较差2个要素进行统计分析(表5)。

表5 不同天气背景下未来24 h最高温度预报的最大占比误差及实况日较差统计Tab.5 Statistics of maximum proportion bias and actual daily range of maximum temperature forecast in the next 24 hours under different weather backgrounds

由表5可见，当模式预报未来24 h为晴天时，水城、盘州、六枝未来24 h最高温度预报的最大占比误差分别为3.2 ℃、2.9 ℃、3.2 ℃，此时3个站最高温度预报准确率可分别提高至85.48%、71.58%、88.99%，平均准确率达82.02%；而对于阴天和雨天，若仍利用最大占比误差来对模式预报进行订正，得到的24 h最高温度预报准确率分别为71.98%和67.79%，将低于采用最大占比日较差来进行预报所得到的预报准确率(77.99%和81.49%)。

因此，在进行最高温度预报时，应根据不同的天气类型选取不同的订正指标。在晴天时，应使用预报误差进行订正，而在阴天和雨天时，应考虑站点本身的日较差进行预报。此时3种不同天气类型相平均的最高温度预报准确率将达到80.50%(表5)，将远高于使用逐月和年平均指标订正方法的预报准确率(表4)。尽管此种订正方法能够明显提升全市的最高温度预报准确率，但受到模式对于天空状态在较长时效下的预报能力不足，以及最低温度预报准确率的影响，此种订正方式对于综合温度预报准确率的提升效果仍存在一定的不确定性。

5 各站点温度预报的订正指标及效果评估

5.1 各站点温度预报的订正指标

前文对全市3个观测站温度预报的订正指标进行了详细讨论。2020年盘州和六枝迁站，因此需要依据迁站前后的温度要素平均差值将相应的指标进行二次订正。

最终采用逐月多时效平均的模式预报误差对六盘水市3个国家基准观测站的最低温度预报进行订正，订正指标如表6所示。而对于最高温度预报，则依据不同的天空类型，晴天采用多时效平均的模式预报误差进行订正，而阴天和雨天则在考虑最低温度预报的基础上采用日较差指标进行订正，具体订正指标如表7所示。

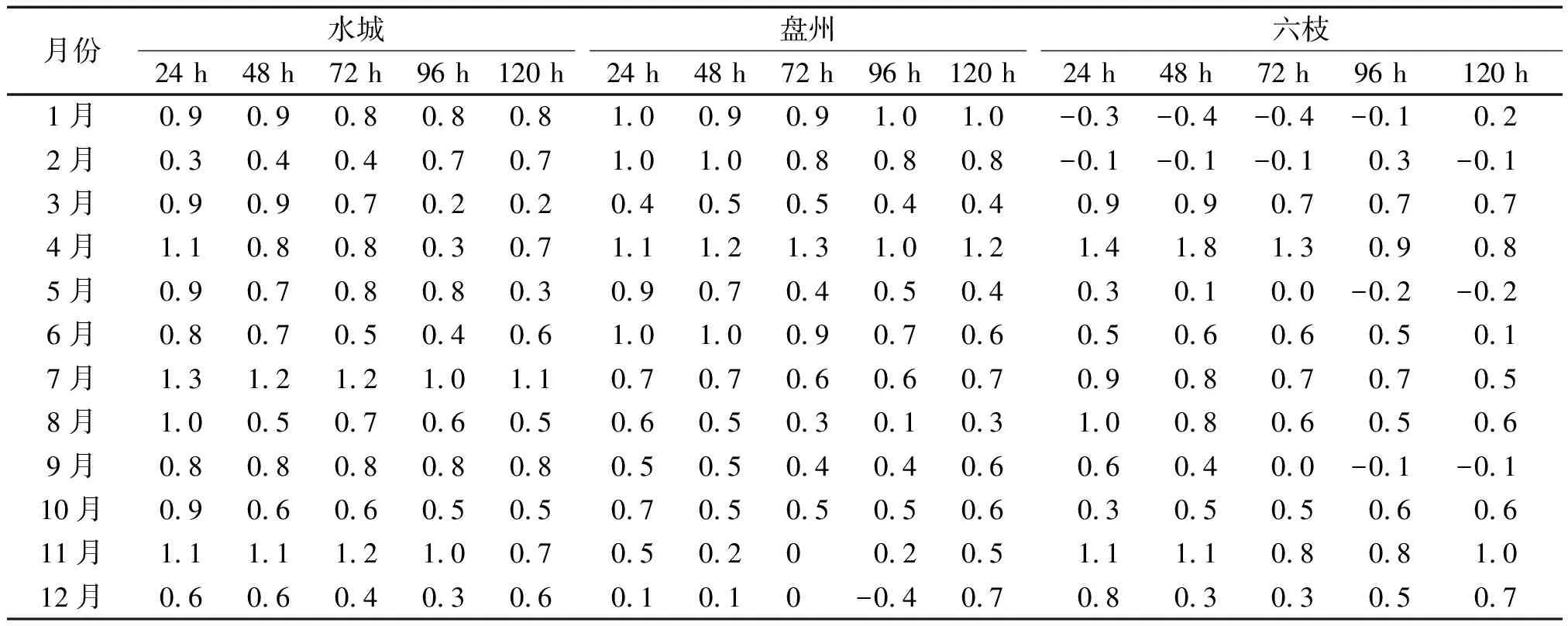
表6 不同月份不同预报时效下各站点最低温度预报的订正指标(单位:℃)Tab.6 Revised indexes of minimum temperature forecast in different months and different forecast time (unit:℃)

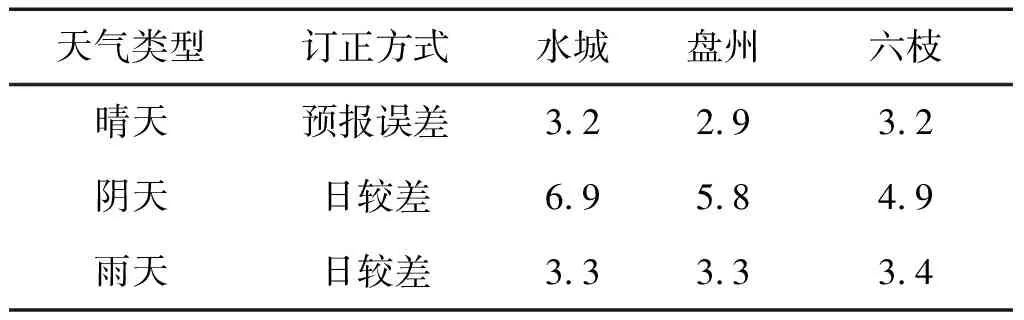
表7 不同天气背景下各站点最高温度预报的订正指标(单位:℃)Tab.7 Revised indexes of maximum temperature forecast under different weather backgrounds (unit:℃)

5.2 订正效果评估

为进一步检验上述指标的合理性和可用性，利用上述指标对2019年12月31日—2020年11月30日六盘水市未来5 d(24～120 h)的温度进行预报，并将预报准确率与实际预报准确率进行对比。

逐月的最低温度预报结果如表8所示，全年平均最低温度预报准确率与实际相当，分别为88.36%和89.16%，从逐月的分布来看，整个夏半年(3—10月)，采用指标订正后的最低温度预报准确率除了6月外，其余月份均超过当前的实际预报准确率，其中9月的盘州预报准确率甚至达到100%；而在2020年初的冬季(1—2月)及11月则与实际的预报准确率差距较大，尤其是隆冬1月。而这是否与1月所存在的热低压与静止锋频繁活动，或者与盘州、六枝迁站后在冬半年(11月—次年2月)呈现出新的预报误差特征有关，有待进一步的分析。

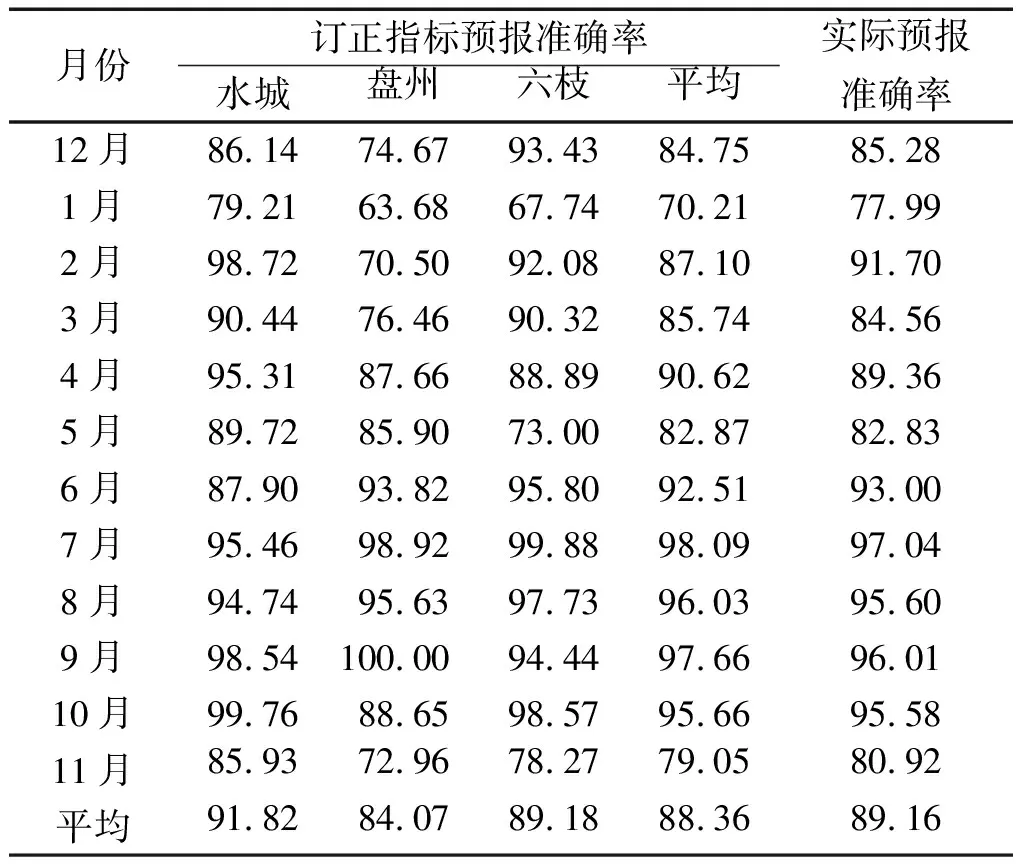
表8 采用订正指标后的全市120 h最低温度预报与实际预报准确率的对比(单位：%)Tab.8 Comparison between the accuracy of 120 h minimum temperature prediction and actual prediction in the city after using the revised index(unit:%)

而对于最高温度预报来说，本文只关注了24 h的预报，且不分月份，只与天气类型有关。由表9可见，在经过指标订正后，六盘水市2020年的24 h最高温度预报准确率为78.64%，要高于实际的24 h最高温度预报准确率(76.61%)。此外，可以看到3个站点的预报准确率最大值和最小值所对应的天气类型各有所不同。水城和六枝雨天的最高温度预报准确率要明显高于晴天和阴天，盘州则是阴天的最高预报准确率最高，晴天最低。

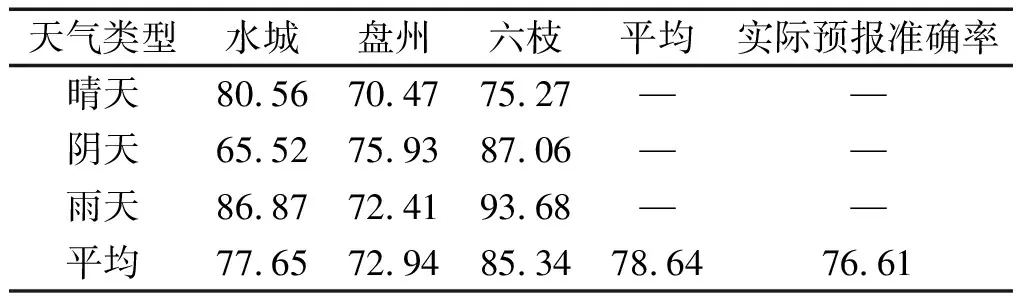
表9 采用订正指标后的全市24 h最高温度预报与实际预报准确率对比(单位：%)Tab.9 Comparison between the accuracy of 24 h maximum temperature forecast after using the revised index and actual forecast(unit:%)

6 结论与讨论

6.1 结论

本文采用气候概率统计的思路，对2018—2019年的EC高分辨率模式2 m温度在六盘水市的预报误差进行分析，并对采用指标订正后的模式预报准确率进行检验。得到如下结论：

①六盘水市3个国家气象观测站的模式温度预报误差均存在随时效的增加而逐渐减小的现象，水城、盘州、六枝3个站各时效平均的最高温度年均预报误差和误差标准差要明显高于最低温度，表明数值模式对最高温度预报较最低温度存在更大的不确定性，尤其是在96 h以外的更长时效上。

②从预报误差及其标准差的年变化来看，对于六盘水而言，模式的温度预报在初夏(6月)可靠性最高，而在春季的3—4月可靠性最低。

③针对未来5 d(120 h)的最低温度预报，采用预报误差最大占比选取了订正指标，对逐月多时效平均的模式预报结果进行订正，对于最高温度预报则根据不同天气类型(晴天、阴天、雨天)采用不用的订正方式和订正指标进行订正，订正后能大幅提高模式的原始温度预报准确率，将六盘水市的120 h最低温度和24 h最高温度预报准确率分别稳定在90%左右和70%以上，

④经过对订正指标在2020年的应用检验，发现订正后的2020年平均最低温度预报准确率与实际相当，而24 h最高温度预报准确率要高于实际预报准确率。其中夏半年(3—10月)的最低温度预报和全年的24 h最高温度预报准确率甚至超过了实际预报。

6.2 讨论

采用气候概率统计的方法所得到的订正指标具有可靠性高，灵活性强的特点，在当地气候稳定的情况下具有较好的适用性，随着统计样本的不断增加，能够在动态调整中将基于该订正指标的温度预报准确率始终维持在一个较高水平。

而基于不同天气类型的最高气温预报订正指标在对阴雨天气的最高温度进行预报时，当前对于天气类型的决定除了数值模式对于天空状况的预报外，还需预报业务人员结合数值预报进行主观判断，因此该指标与数值模式本身的变动无关，只要数值模式的形势预报精度得到提高，最高温度的预报准确率将随之得到提高。同时，如何在不同气象要素预报和天气类型之间建立合适的线性关系，进一步降低业务人员的在天气类型判断中的主观性，也是下一步研究的工作重点。