底部透空不透水建筑物波压力研究

孙 涛，王英波，孙洪涛

（1.日照实华原油码头有限公司,山东 日照 276800；2.海博泰科技(青岛)有限公司,山东 青岛 266010）

防波堤和码头等水工建筑物是港区重要的组成部分，其具有抵御外海波浪，维持港内水域平稳以利于船舶停靠等优点，波浪作用下不同结构形式的水工建筑物要维持其自身稳定，波浪荷载是主要研究内容之一。相关学者对不同结构水工建筑物的波浪力作用进行了研究，如：李翔等[1]采用不规则波浪,对透水斜坡上不同开孔率混凝土面板受到的波浪打击力进行研究，分析了打击力随各影响因素的变化特性，给出了波浪打击力的统计分布规律；Cuomo 等[2]通过物理模型试验研究了波浪对竖墙的作用力，并总结出竖墙表面波压力计算公式；Neelamani 等[3]对规则波作用下的冲击力进行较为系统的试验；冯卫兵等[4]采用物理模型试验的方法，研究在不规则波作用下最大打击力位置与相对深度的变化规律，拟合得到最大相对波压力公式和波压力沿斜坡分布规律；王登婷[5]通过物理模型试验研究防浪墙底面高程对其迎浪面及底面波浪压强及整体稳定性的影响；柳玉良等[6]通过模型试验研究了圆形沉箱水平波浪力与浮托力的分布情况，并与现有直立堤理论公式进行比较。

底部透空不透水直立建筑物是港口工程建设中的一种新型结构，该型建筑物底部不透水，透空部分通过设置钢筋混凝土墩安放在基床上，在波吸力作用下使该型建筑物更加稳定，在防波堤和码头中都可使用，直立建筑物顶部设置挡浪墙，增加顶面高程减少越浪以满足内侧船舶靠泊，但波浪遇直立建筑物易产生驻波，致使迎浪面和底面受波浪力的作用增大，对底部透空不透水直立建筑物的稳定产生影响，存在造成局部或整体失稳安全隐患。本文通过波浪断面物理模型试验，对不同水深下底部透空不透水直立建筑物的波压力实测数据开展研究，并根据《港口与航道水文规范》[7]规定的波浪力计算方法与物理模型试验波浪力结果进行对比，分析总结波浪力分布规律，为类似工程设计和理论研究提供参考。

1 模型试验

1.1 试验设备

试验在中国海洋大学山东省海洋工程重点实验室开展，该不规则波水槽长50.0 m、宽1.2 m、深1.2 m。水槽一端为低惯量直流式电机不规则造波机，可模拟正弦波和椭圆余弦波等规则波以及国内外常用的频谱（PM 谱、B 谱、JONSWAP 谱等），造波机可产生波高范围为3～50 cm，波浪周期范围0.5～50 s。水槽另一端为消能设施，其反射率＜5%，满足试验规范《水运工程模拟试验技术规范》[8]要求。

1.2 试验参数

建筑物透空率为12%，率定试验波浪要素时，在水槽内建筑物前制作坡度为1∶25 的斜坡，直立式模型安放于斜坡顶水平位置且波浪平稳段，模型底部迎浪处采用透空型式，底部后方采用不透水处理，试验模型布置见图1。

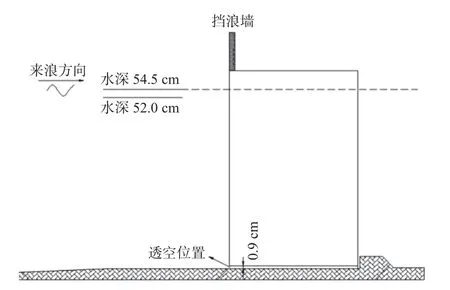
图1 试验模型布置Fig.1 The overall layout of the testedmodel

为测量建筑物波压力分布情况，根据《水运工程模拟试验技术规范》[8]和《防波堤与护岸设计规范》[9]，在建筑物迎浪面和模型底部加密布置一定数量的压力传感器，模型同一高度处布置2 个传感器，便于校对数据。波压力传感器布置见图2，其中迎浪侧20 个、底面8 个。

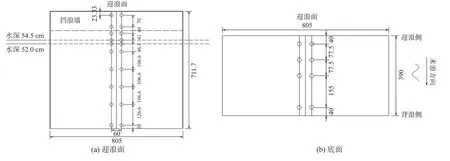
图2 波压力传感器布置Fig.2 Layout of the wave pressure sensors

1.3 试验方案

为分析相同波要素、不同水深下波浪力的分布规律，测试水平总力最大时各测点波压力。断面试验采取2 种方案：方案一，工况1 和工况2 为相同波要素；方案二，工况3 和工况4 为相同波要素。

本次试验选取2 种水深，分别为54.5 和52.0 cm。试验工况见表1。

表1 试验工况Table 1 Working conditions for the test

2 试验结果

为保证试验精度，每种工况波压力试验采集有效数据4～5 次，同一高程的2 个测点剔除异常值后取平均值作为该高程处的波压力值。数据处理后得到水平总力最大时刻的同步波压力分布值，通过积分得到模型迎浪面上每延米水平波浪总力。正负波压力规定为：水平波浪力计算中，沿来波方向为正，反向为负；垂直力计算以向上为正，向下为负。

使用Matlab 软件，采用上跨零点法对采集到的点压强数据进行分析，结果表明：水平力最大值与浮托力最大值并不同步发生，迎浪面波压力近似呈梯形分布，建筑物底部的波压力从外侧向内侧相差较小。方案一波峰和波谷作用下水平总力最大时各测点波压力见表2，波峰和波谷作用下水平总力最大时各测点波压力分布见图3；方案二波峰和波谷作用下水平总力最大时各测点波压力见表3，波峰和波谷作用下水平总力最大时各测点波压力分布见图4。

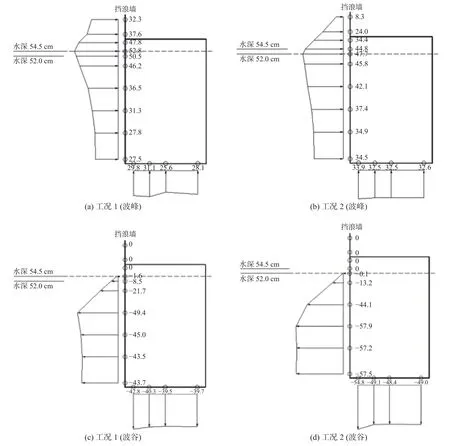
图3 方案一水平总力最大时各测点波压力（kPa）Fig.3 The wave pressure (kPa) at each measuring point when the horizontal total force is maximum in Scheme 1

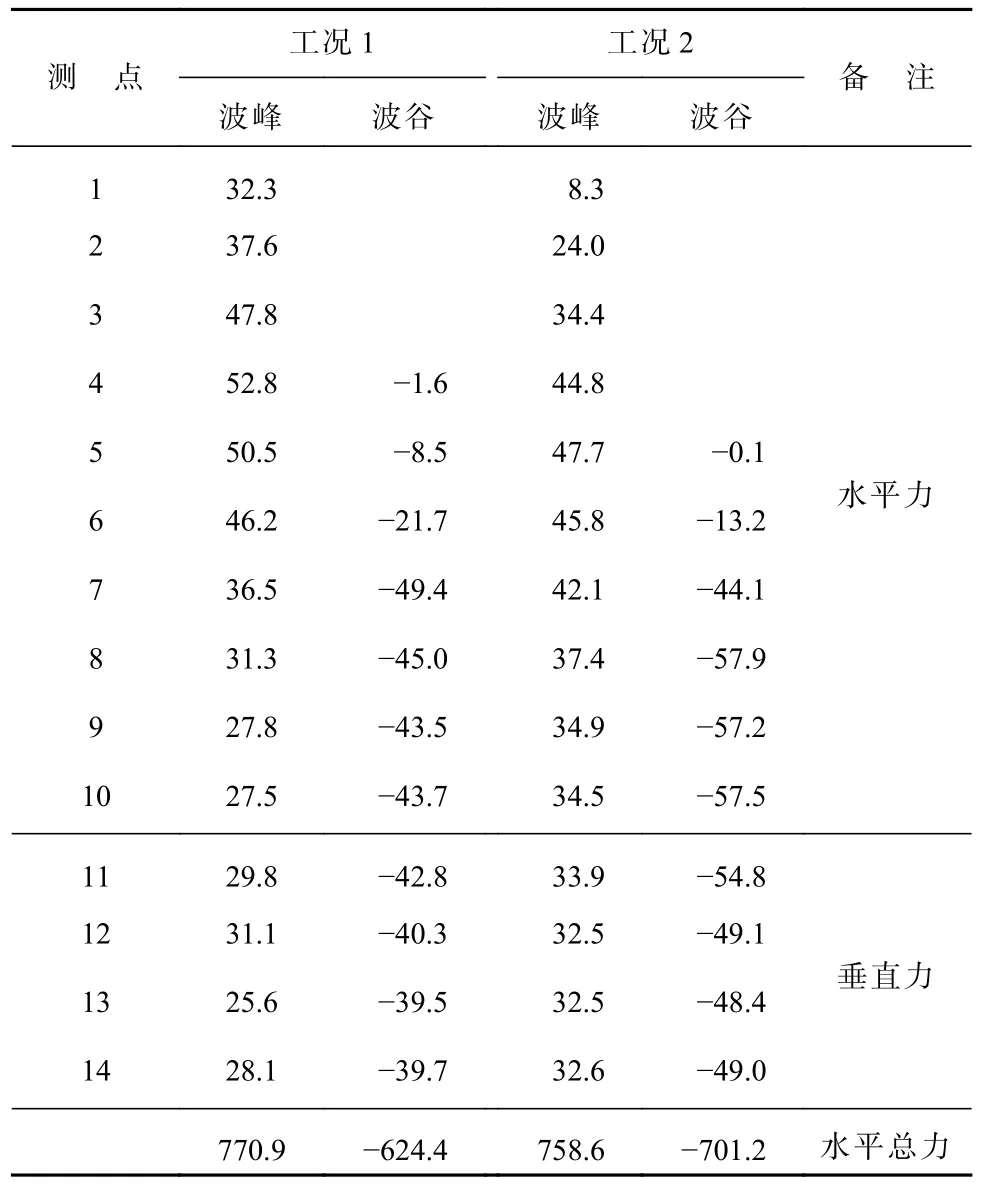
表2 方案一水平总力最大时各测点波压力（kPa）Table 2 The wave pressure (kPa) at each measuring point when the horizontal total force is maximum in Scheme 1

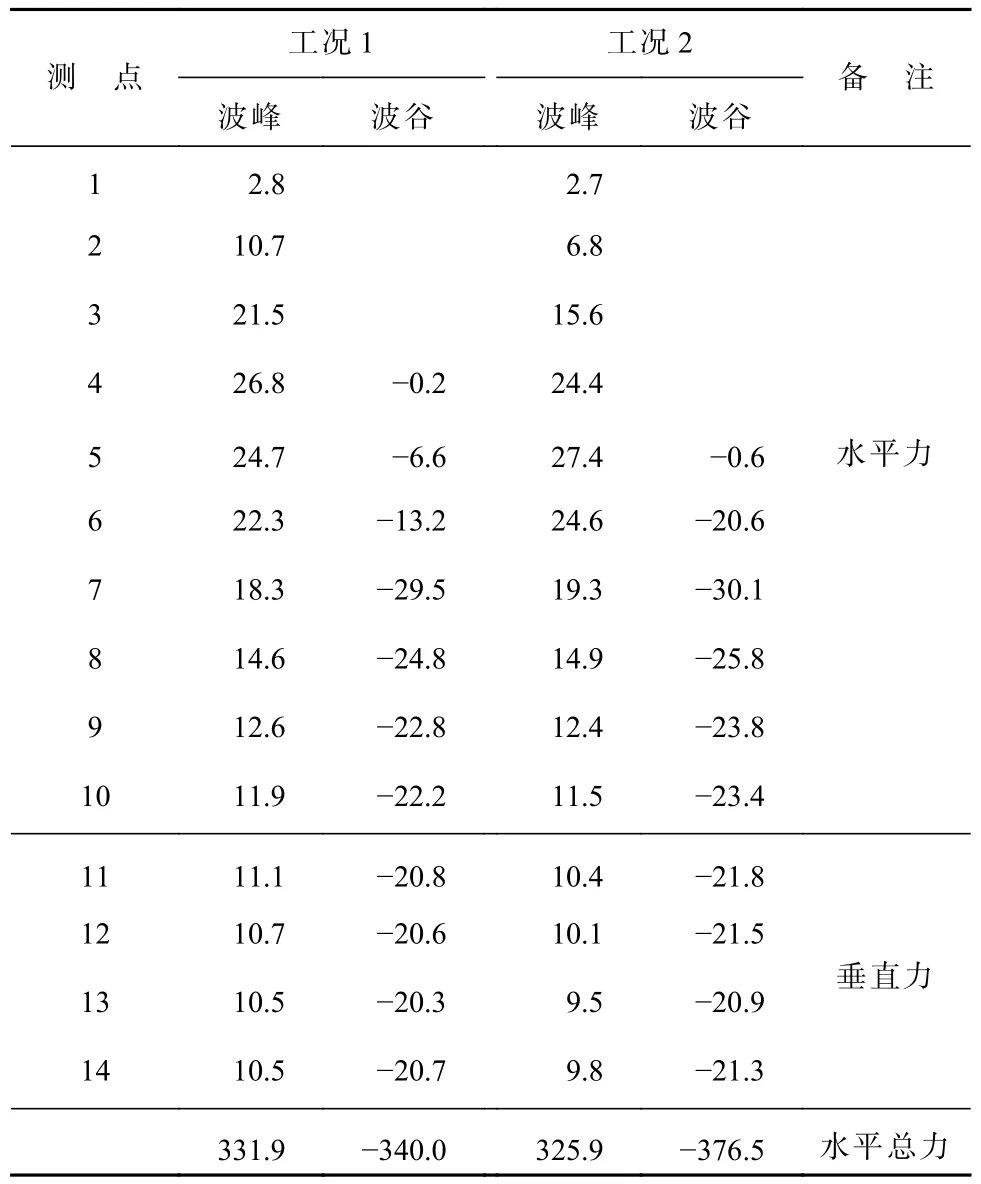
表3 方案二水平总力最大时各测点波压力（kPa）Table 3 The wave pressure (kPa) at each measuring point when the horizontal total force is maximum in Scheme 2

由表2 和表3 可知，底部透空不透水建筑物最大压强发生在静水位处，随着水深的增加迎浪面上波压力减小；当波高和周期相同、水深不同时，迎浪面波压力分布随水位的降低静水位以上测点波压强随之减少，静水位以下各测点波压强增大。

对方案一和方案二在不同水深、波峰及波谷作用下的波浪力分析可知，相同波要素下，波峰作用时大水深迎浪面水平总力大于小水深，波谷作用时迎浪面的水平总力则反之。

其中，工况1 波峰作用下迎浪面水平总力比工况2 大1.5%，工况3 波峰作用下迎浪面水平总力比工况4大1.8%；工况1 波谷作用下迎浪面水平总力比工况2 小12.3%，工况3 波谷作用下迎浪面水平总力比工况4小10.7%，

由图3 和图4 可知，对于底部透空，底部和两侧不透水建筑物，由于建筑物后方底部透空不透水，底面波压力数值差别较小。

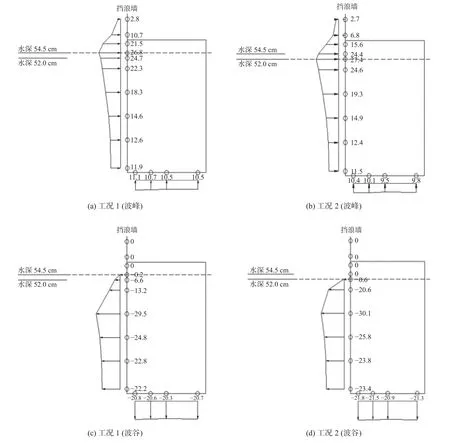
图4 方案二水平总力最大时各测点波压力（kPa）Fig.4 The wave pressure (kPa) at each measuring point when the horizontal total force is maximum in Scheme 2

3 波压力试验值与计算值比较

因《港口与航道水文规范》[7]未对底部透空不透水直立建筑物底面波浪力的计算进行阐述，所以本文只按照规范计算了该型建筑物迎浪面波浪力，并与物理模型试验结果对比，分析总结波浪力分布规律。根据《港口与航道水文规范》[7]可知，直立建筑物前波浪波态均为立波，2 种方案波浪力计算方法如下。

1）方案一

波峰作用下立波作用力按式（1）～式（4）计算：

式（1）～式（4）中：hs为波浪中线超出静水面的高度（m）；H为建筑物所在处进行波波高（m）；L为波长（m）；d为建筑物前水深（m）；pd为水底处波浪压力强度（kPa）；γ为水的重度（kN/m3）；ps为静水面处波压力强度（kPa）；pb为墙底处波压力强度（kPa）；d1为基床上水深（m）。

波谷作用下立波作用力按式（5）～（7）计算：

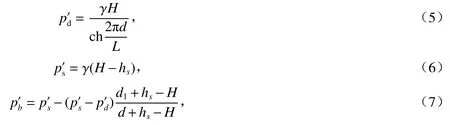
2）方案二

波峰作用下立波作用力按式（8）～式（10）计算：

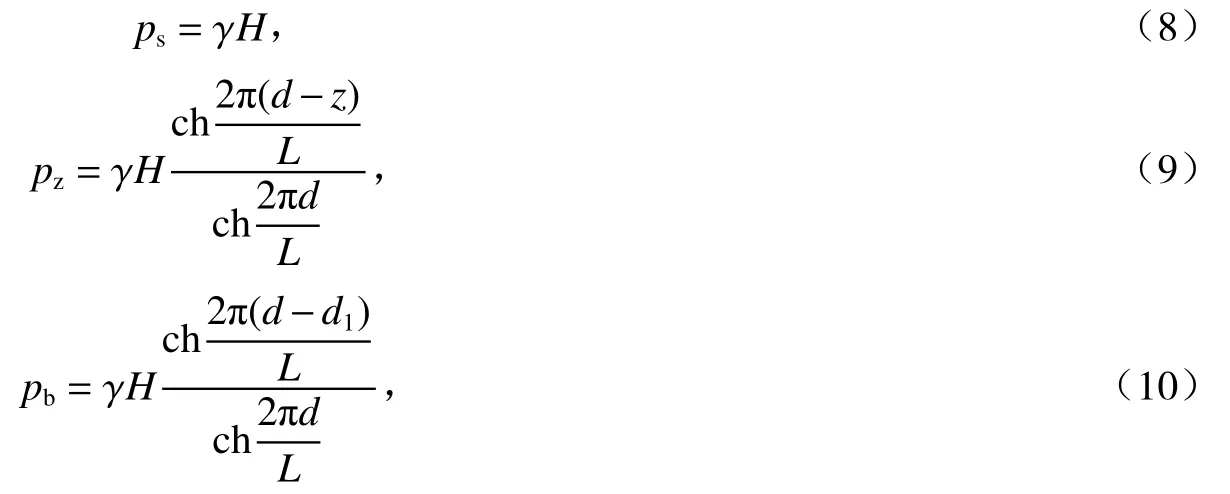
式（8）～式（10）中：ps为静水面处波浪压力强度（kPa）；γ为水的重度（kN/m3）；H为建筑物所在处进行波波高（m）；pz为静水面以下深度Z处的波浪压力强度（kPa）；d为建筑物前水深（m）；z为静水面以下深度（m）；L为波长（m）；pb为墙底处波浪压力强度（kPa）；d1为基床上水深（m）。

方案二波谷作用下立波作用力同样按式（5）～式（7）计算。

方案一计算结果见表4，方案二计算结果见表5。由表4、表5 与表2、表3 对比，波峰作用下各点波压力试验值小于规范计算值，波谷作用下，由于底部透空结构的影响，除水位附近点位试验值和计算值接近之外，其他点位试验值大于规范计算值。

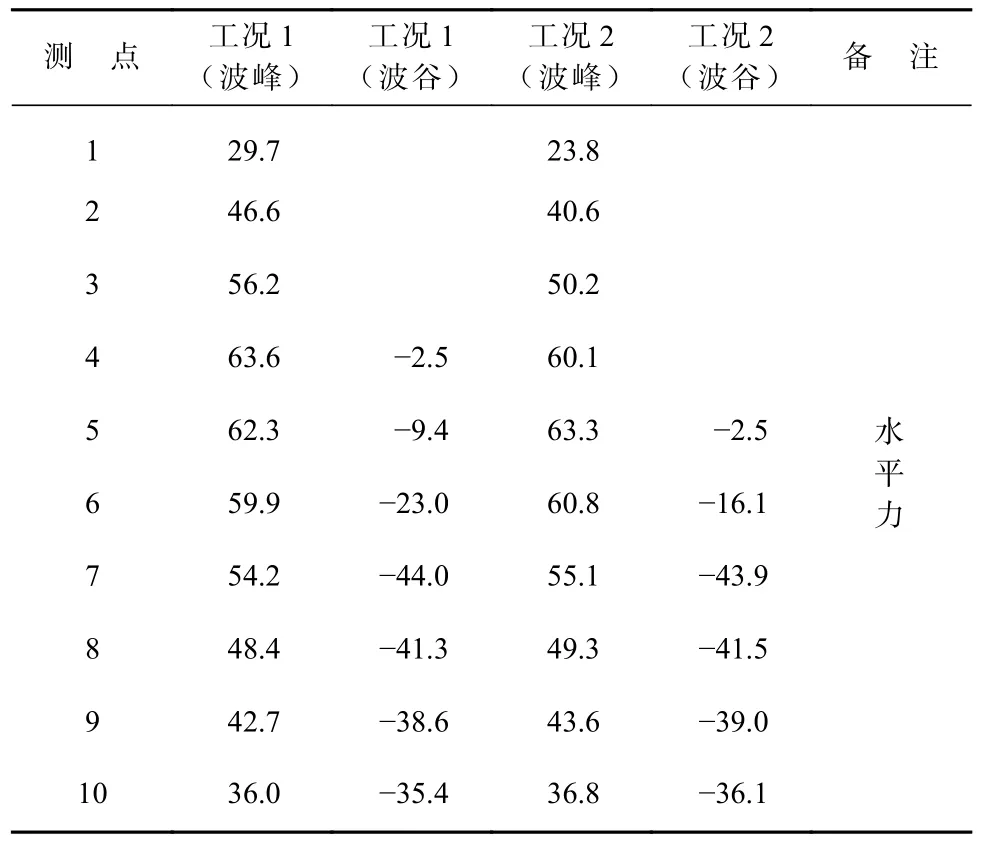
表4 方案一各点波压力强度计算值（kPa）Table 4 Wave pressure (kPa) at each measuring point in Scheme 1

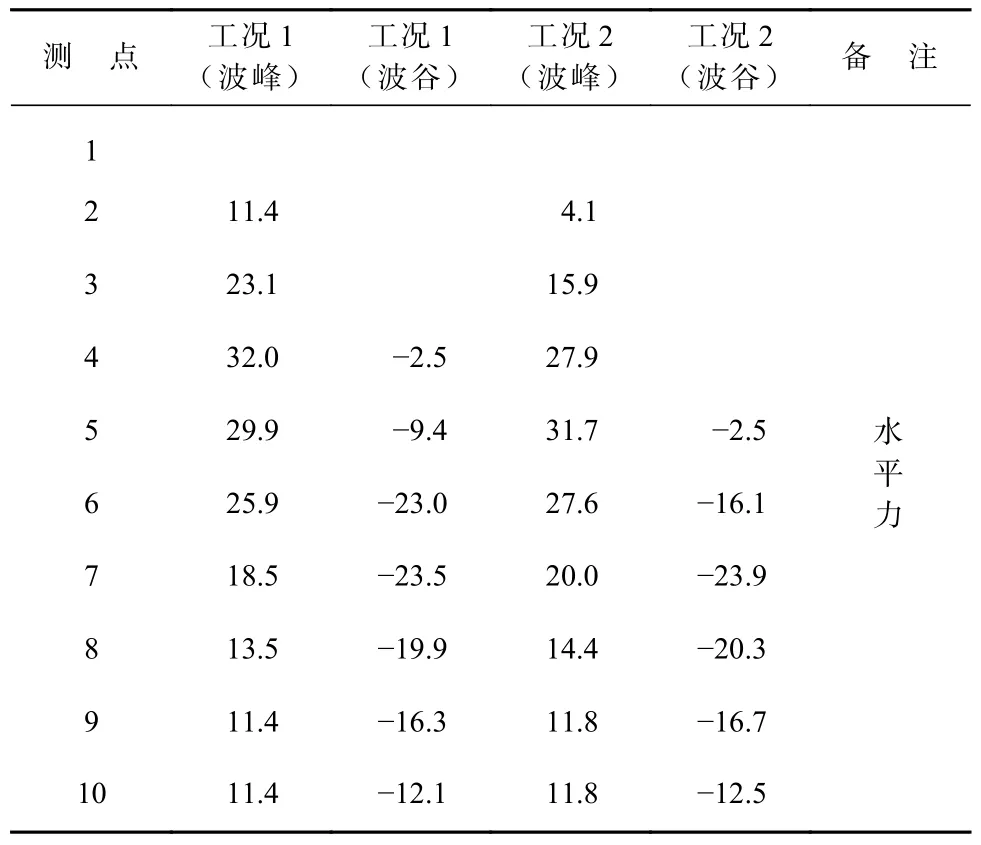
表5 方案二各点波压力强度计算值（kPa）Table 5 Wave pressure (kPa) at each measuring point in Scheme 2

4 结论

本文通过物理模型试验，针对底部透空不透水建筑物的波压力进行测试，并根据规范计算结果与试验结果对比分析，研究了不规则波作用下底部透空不透水建筑物迎浪面及底面波压力分布规律，得出以下主要结论。

1）底部透空不透水建筑物最大压强发生在静水位处，随水深的增加迎浪面上波压力减小。波要素相同，迎浪面波压力随着水位的降低，静水位以上测点波压强减小，静水位以下各测点波压强增大。

2）不同水深，相同波要素下，大水深时波峰作用下迎浪面水平总力比小水深时大，而大水深时波谷作用下迎浪面水平总力比小水深时小。

3）与传统水工建筑物相比，模型底部透空不透水时底面测点波压力数值较为接近，波压力分布既不是呈梯形分布，也不是呈合田良实[10]提出的三角形分布。

4）通过对该型直立建筑物试验研究及波压力计算结果比较，波峰作用下各点波压力试验值小于规范计算值，波谷作用下受底部透空结构的影响，试验值大于规范计算值。