用turtle模块绘制一次函数图像

吴欣瑶

本例中我们通过Python编程编写一个具有简单交互界面的小程序。用户输入一次函数y=kx+b中k，b两个常数的值就可以画出函数图像（图1）。

首先做出一个图形用户界面（GUI）来接收数据。此程序使用Python的tkinter模块来做GUI。tkinter 共有三种几何布局管理器，分别是pack布局、grid布局、place布局。这三种均用于同一父组件下的组件布局，但是也是有区别的。pack按添加顺序排列组件;grid按行列形式排列组件;place允许程序员指定组件的大小和位置。

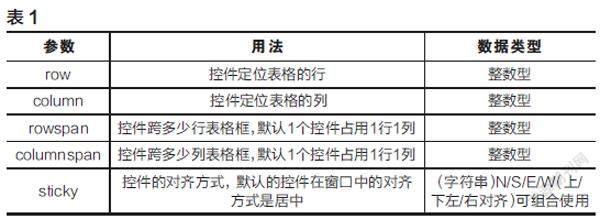
这里用简便易用的grid来布局，它的基本参数及用法如表1所示。

通俗地讲，grid布局就是把每个控件放置在单元格中，整个窗体就是一张表格。因此可以使用Excel或WPS表格等工具来做一个界面的效果图，如图2所示。值得注意的是，参数row和column都是从0开始的，所以应修改成图3所示的格式：

接下来就把这个界面书写成代码，如图4。

代码中使用通配符“*”引入了三个模块。tkinter模块用于图形界面编程，turtle模块用于绘制坐标系与函数图像，math模块用于计算函数图像与x轴的夹角。

此处创建了两个特殊的字符串变量v1和v2，它们是StringVar（字符串变量）。这种变量的特殊之处在于它需要通过get（）方法来访问里面的值。在后面编写程序获取值的时候就会用到get（）方法了。然后设置两个输入框（e1、e2）的textvariable参数分别为v1和v2，用户输入到输入框e1和e2中的内容就会分别被放入变量v1和v2中。

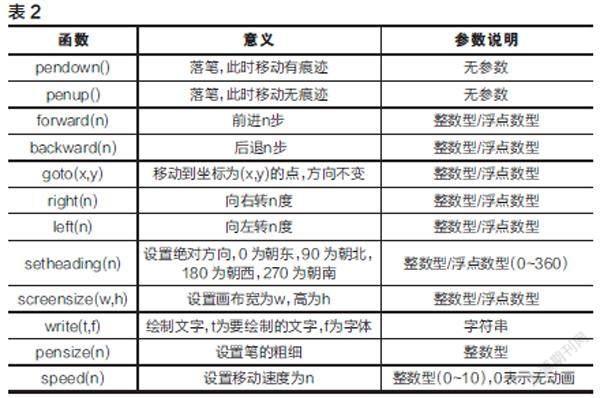
在绘制函数图像之前，需要建立一个平面直角坐标系xOy（x轴，y轴以及以它们的交点O为原点建立的坐标系称为xOy）。坐标系使用turtle模块绘制，turtle模块的部分函数及意义如表2所示。

2.绘制箭头

在绘制x轴与y轴时，都需要画一个小箭头表示正方向，那么如何在一条直线的末端画出箭头呢？turtle画箭头的路径如图5所示：

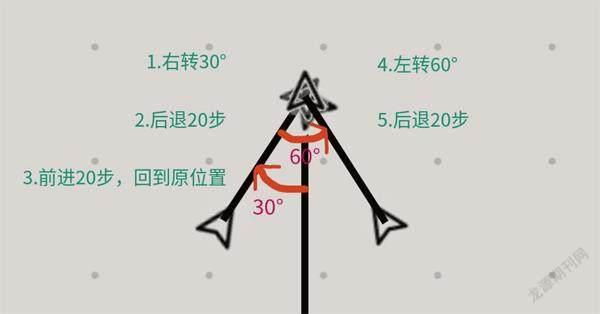
将绘制箭头的步骤（1.右转30°;2.后退20步;3.前进20步，回到原位置; 4.左转60°; 5.后退20步）写成一个函数，以便后续使用，代码如图6：

接着绘制坐标轴，turtle绘制坐标轴的路径如图7所示：

预设坐标系宽600高800。将绘制平面直角坐标系的步骤写成代码，如图8：

在每次绘制完箭头后（步骤4、步骤11），都会向右转120°。这是因为在arrow（）函数绘制完箭头后，小海龟（笔）的朝向是轴线朝向偏左30°，为了方便后面前进30步和绘制文字的步骤，便向右旋转120°，使其朝向变成轴线朝向偏右90°，即与轴线垂直。

在绘制字母x、y以及原点O时，用到了write（）函数。Write（）函数的font参数需要传入一个三元组，元组的第一项是字体名;第二项是文字大小;第三项是文字样式，一般有三种文字样式：正常（normal）、粗体（bold）、斜体（italic）。

在程序中，仅仅知道函数的解析式，想要确定直线并用turtle绘制出来就必须有三步操作：第一步，取直线上的两点（任意两点即可）;第二步，求出两点的水平距离和铅垂距离，并通过反三角函数atan得到图像与x轴的夹角的弧度值;第三步，将弧度值转换为角度值（图9）。

首先写一个事件响应函数click（event），用get（）函数从字符串变量v1和v2中取得用户输入的值。get（）函数的返回值类型是字符串，而字符串不能直接参与数字运算，所以需要把它们转换成整数或是浮点数。但为了支持用户输入运算表达式，这里使用eval（）函数，eval（）函数可以将一个字符串表达式执行并返回结果。把eval（）函数返回的值直接储存到变量k、b中，方便后面计算使用（图10）。

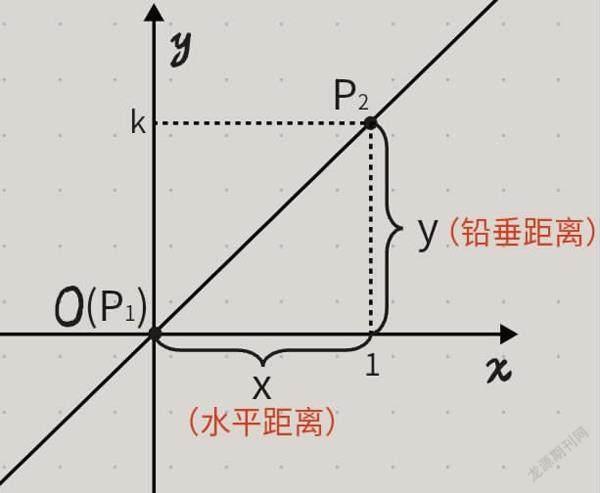
除了正比例函数之外的其他一次函数的图像，都会与y轴和x轴分别有一个交点（如图中点P1、P2）。这两个交点和原点正好构成一个直角三角形，那么两交点的水平距离和铅垂距离，如图9中x、y所示，这两条线段就相当于是直角三角形的两直角边。在这里使用反三角函数atan，把y/x带进去，即atan（y/x），就可以求得函数图像与x轴的夹角θ的弧度值。注意，atan函数计算结果（rad）是弧度值，不是角度值，因此需要进行转换。转换公式为：1弧度=（180/π）°。在代码中π取近似值3.1415，精度就足够了。转换之后就得到了函数图像与x轴的夹角θ的角度值（angle）。接着，使用goto（）函数移动到函数图像与x轴的交点，即点P2。然后判断斜率k（k≠0）的正负性，如果斜率k是正数，则函数图像向上倾斜，否则向下倾斜。知道了倾斜方向就可以根据夹角θ的角度值（angle）用setheading（）函数设置turtle的绝对方向。然后再沿着这个方向后退400步再前进800步就能绘制出一条准确的直线（函数图像）了。

众所周知，正比例函数是一种必过原点的特殊一次函数（图11）。所以，由此就知道了该函数图像上的一点（原点O，也是P1），再取函数图像上当x=1时的点（1，k）就能构成一个直角三角形，然后使用atan函数并转换成角度，方法与非正比例函数（其他一次函数）中所述方法相同。最后，用b1.bind把事件响应函数click和左键单击的事件（<Button-1>）绑定在一起，如此一来当用户使用鼠标左键单击按钮b1时，就会执行函数click中的操作（图12）。