从力学角度浅谈平面机构传动角的求解
高阁
从力学角度浅谈平面机构传动角的求解
高阁
(江苏科技大学 机械工程学院,江苏 镇江 212100)
机构传动角常用来判断平面机构的传力性能,但现有教材并未直接给出传动角的定义,而需要依赖压力角求解,容易产生歧义性从而造成学生理解和运用的困难。本文从力学的角度出发解析传动角的实际物理含义,引入有效/无效驱动力的概念,在保证教材传动角原主体定义不变的前提下通过补充说明给出了传动角的准确定义,并基于该途径给出了常用机构的传动角的求法。在此基础上进一步讨论了最小传动角的求解。通过若干实例表明该定义方式简单明了、具有唯一性,更加容易被学生接受及使用,完善了机械设计教材中的相应基本概念。
传动角;压力角;力学
压力角和传动角是机械设计中的重要参数,它们直接影响机械传动效率和是否发生自锁。在连杆机构设计中,除了要满足运动要求外,还应具有良好的传力性能,以减小结构尺寸和提高机械效率。为了度量方便,工程上习惯用传动角来判断传力性能。根据传动角理论,通常传动角越大,表明机构传力效果越好,效率越高;反之,越小,机构传力越费劲,传动效率越低[1]。机构运转时,传动角是变化的,为了保证机构正常工作,避免传动效率过低并防止机构出现自锁现象,工程上必须规定最小传动角min的下限。对于一般机械,通常取min≥40°。对于大功率机械,可取min≥50°;对于小功率的控制机构和仪表或不常使用的操纵机构,min可略小于40°,只要不发生自锁即可[2-4]。
虽然传动角理论在机构学中应用广泛,但目前大部分教材对传动角的定义采用间接的形式,即“压力角的余角为传动角”[3,5-6]。由于传动角的存在依赖于压力角而并未直接给出,学生们在使用作图法求解时中常常面临压力角有两个余角的情况,因而求得的传动角不具有唯一性,无法确定哪个才是正确的。针对该问题,一些学者提出传动角的新定义以确保该物理量的唯一性,但其与教材现有定义差别较大[7-8]。为解决上述问题,本文力图采用追本溯源的思路,从力学本质出发揭示传递角的物理含义,力求在不改变传统教材传动角定义主体的基础上进行适当补充说明来确保其求解的唯一性、正确性,最终目的为方便学生在应用图解法时高效、快速得出机构的传动角,且结果简单可靠,便于掌握和使用。
1 传统传动角定义的模糊性
现有教材及教学方法求传动角的方式是先通过作图法求出机构的压力角,然后再求其余角得到传动角。以图1的曲柄摇杆机构为例,若不考虑各运动副中的摩擦力及构件重力和惯性力的影响,则由主动件经连杆传递到从动件上点的力将沿方向,而力与点速度正向之间的夹角(锐角)称为机构在此位置时的压力角(pressure angle)。在连杆机构设计中,为了度量方便,习惯将压力角的余角称为机构在此位置时的传动角(transmission angle)[9-11]。传动角g愈大,对机构的传利愈有利。所以在连杆机构中常用传动角的大小及变化情况来衡量机构传力性能的好坏。
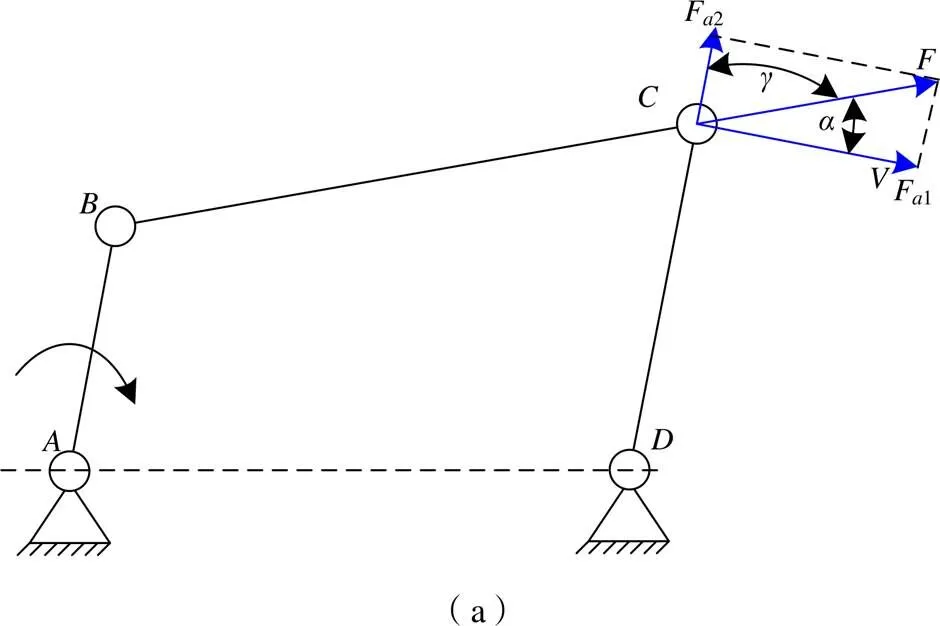
通常在实际使用时可以根据定义很容易得到压力角,但由于其余角并不唯一,作图时会出现图1(a)、(b)两种情况,此时的传动角按照教材定义都是压力角的余角,但实际上只有图1(a)的画法是正确的。出现该问题的直接原因是压力角的余角不唯一,导致传动角歧义,其背后的根本原因是由于现有教材并未直接给出传动角的定义,而是依赖于压力角间接定义,从而导致其概念的模糊性。需要指出的是,压力角和传动角是具有同等地位的结构参数,在传动角度上并不存在“依附”或“从属”关系,只是在几何上具有互余的关系。因此,为更好的理解二者的意义,有必要重新审视二者背后的力学本质。
2 从力学角度审视传动角的物理意义
机构是用来传递力和运动的构件系统[5],因此提出传动角的初衷是因为该物理量便于衡量机构传动性能的好坏,准确来说,传动角反映了驱动力和运动方向一致性的程度。通常机构在使用过程中,驱动力并不是全部作为有用功带动从动件运动,根据力学三角形法则,可以分解为有效驱动力和无效驱动力两部分(这里包含有效/无效驱动力为0的特例)。以图1(a)为例,驱动力可以正交分解为垂直于杆方向的分力F1和沿杆方向的分力F2,其中F1=sin为有效驱动力,它带动从动件杆绕点做往复摆动,而且越大,受力方向越接近运动方向,因而F1越大,绕点的转矩越大,传动就越有利;而竖直分力F2=cos=sin为无效驱动力,由于其方向垂直于从动件运动方向,因而它不做功而只对其产生拉(压)作用,且越小,受力方向越远离运动方向,从而越大,该拉(压)力越大。按照教材传动角的物理含义可知,为该机构的传动角。与之相对的,假如按照图1(b)所示作图,则该传动角的物理意义不明确。其中F1可部分视为有效驱动力,虽然其方向与速度方向共线做正功,但其数值大小无法直接用和来表达。此外,F2没有实际物理含义,一方面由于其方向与速度方向并不垂直,无法直接视为无效驱动力。另一方面F1、F2和不满足力学三角形法则,因而也无法单纯将F1和F2与视为分力与合力的关系。综上,该图示所求的传动角是错误的,其对应的物理概念模糊,它无法根据本身数值大小来定性反映机构的传力性能好坏。
通过上述分析可以发现,根据传动角提出的工程背景及初衷,传动角一定是可以直接反映机构从动件驱动力和其运动方向一致性程度的物理量,且越大,驱动力越接近运动方向,因而有效驱动分量越大,无效驱动分量越小,机构的传动性能越好。而根据力学三角形法则特性,作图时当且仅当驱动力位于传动角和压力角之间时,驱动力可以分解为有效驱动力和无效驱动力两部分。因此,对于传动角,在不改变传统教材定义方式的前提下做如下补充以保证其求解的唯一性:压力角的余角为传动角,且两者分别位于从动件驱动力的两侧。按照这种方法来重新定义传动角,可以直接得出图1(a)的传动角正确、图1(b)的传动角错误的结论。该定义使得传动角的物理意义更加明确,即传动角反映了从动件驱动力与其运动方向的接近程度,且越大时,两者越接近,有效驱动力越大,所做有效功越多,机构的传动效率就越高。这种定义方式对传统教材的定义做了有效地补充,避免了压力角余角的不唯一性而导致传递角的歧义性、模糊性,同时该判断法迅速快捷,简单可靠,所得结果唯一。
3 采用新方法图解常用机构的压力角/传动角
为证明该定义的高效性,选取下列常用机构,用作图法求解其压力角及传动角。这里不考虑各运动副中的摩擦力、构件重力和惯性力的影响。
3.1 曲柄滑块机构
图2为一曲柄摇杆机构,为曲柄,为连杆,为滑块。在图2(a)中,曲柄为主动件,滑块为从动件。从动件驱动力方向沿杆,从动件速度方向水平向右,两者间的夹角为压力角。根据前面的定义可知,传动角应位于下侧,如图2(a)所示。在图2(b)中,滑块为主动件,曲柄为从动件。从动件驱动力方向沿杆,从动件速度方向垂直于杆,两者间的夹角为压力角,同样传动角需位于下侧保证驱动力在两者之间。
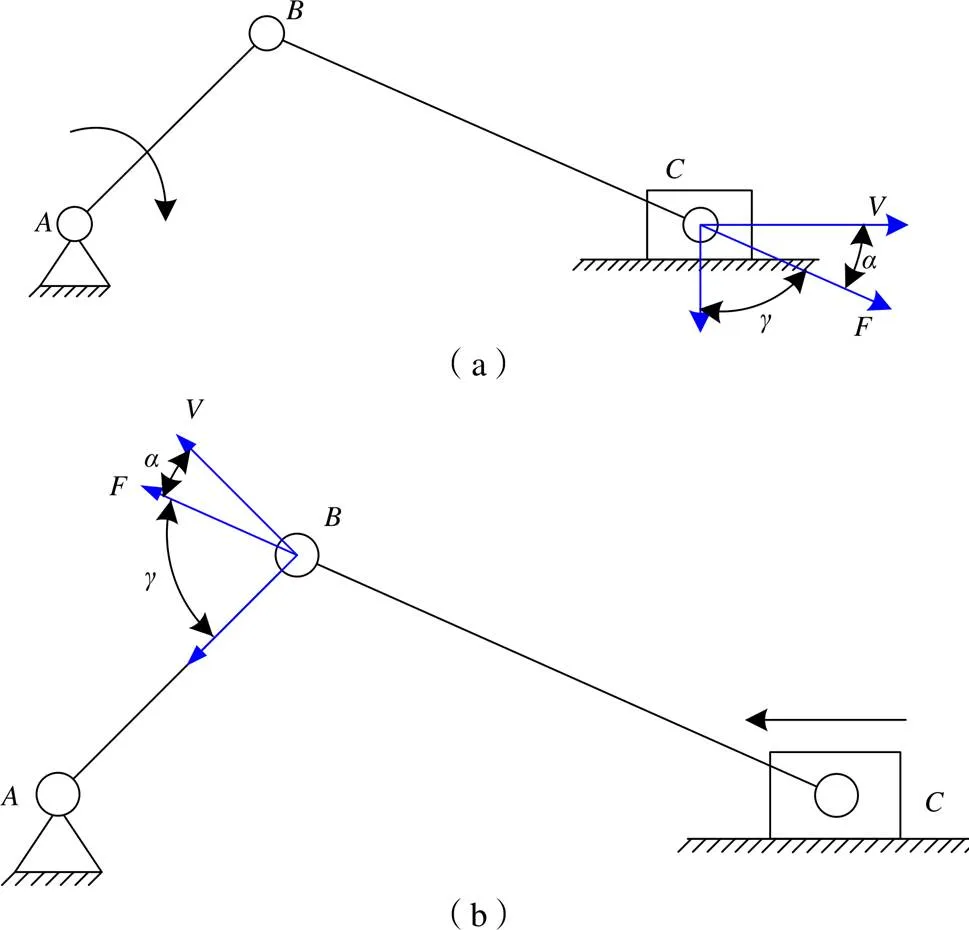
图2 曲柄滑块机构
3.2 曲柄摇杆机构
图3为一曲柄摇杆机构,为机架,为曲柄,为摇杆,为连杆。需要注意,与图1不同的是,杆为主动件,杆为从动件。因此压力角作图应选择在从动件杆的点。从动件驱动力方向沿着杆,从动件速度方向垂直杆,两者间的夹角为压力角。按照新定义传动角应为和杆件的夹角,从而保证和位于两侧,如图所示。通过图1和图3的这两个例子可以看出,当机构处在同一位置,若原动件和从动件的选取不同,则压力角和传动角可能不同,这是在学习过程中需要格外注意的。
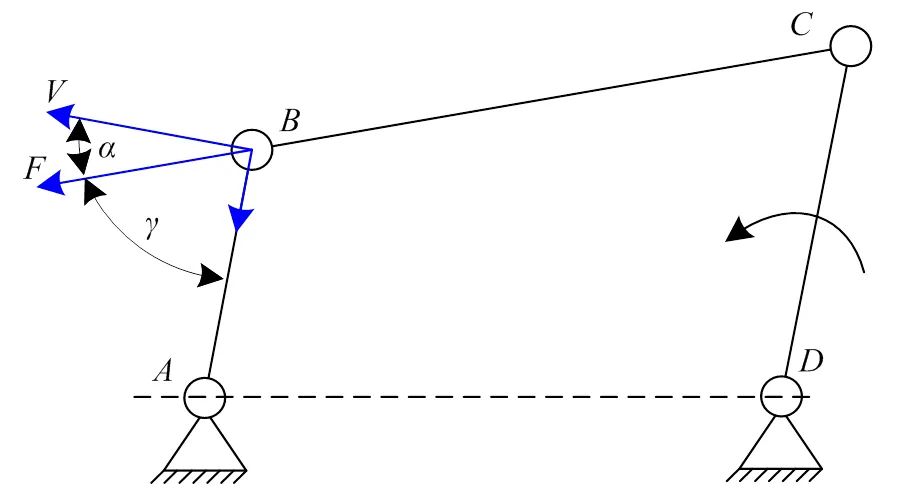
图3 曲柄摇杆机构
3.3 导杆机构
图4为一导杆机构,为机架,为曲柄,为摇杆,为滑块。在图4(a)中,摇杆为主动件,曲柄为从动件。从动件驱动力方向垂直于杆,从动件速度方向垂直杆,其压力角和传动角如图4(a)所示,从而保证和位于两侧;在图4(b)中,曲柄为主动件,摇杆为从动件。从动件驱动力方向垂直于杆,速度方向也垂直于杆,因而压力角=0°,传动角=90°。需要特别指出的是,对于图4(b)机构,在运转过程中压力角与传动角的大小是不变的,即压力角≡0°,传动角≡90°,因此其具有很好的传力性能,常用在回转式油泵、牛头刨床、简易插床等机械中。
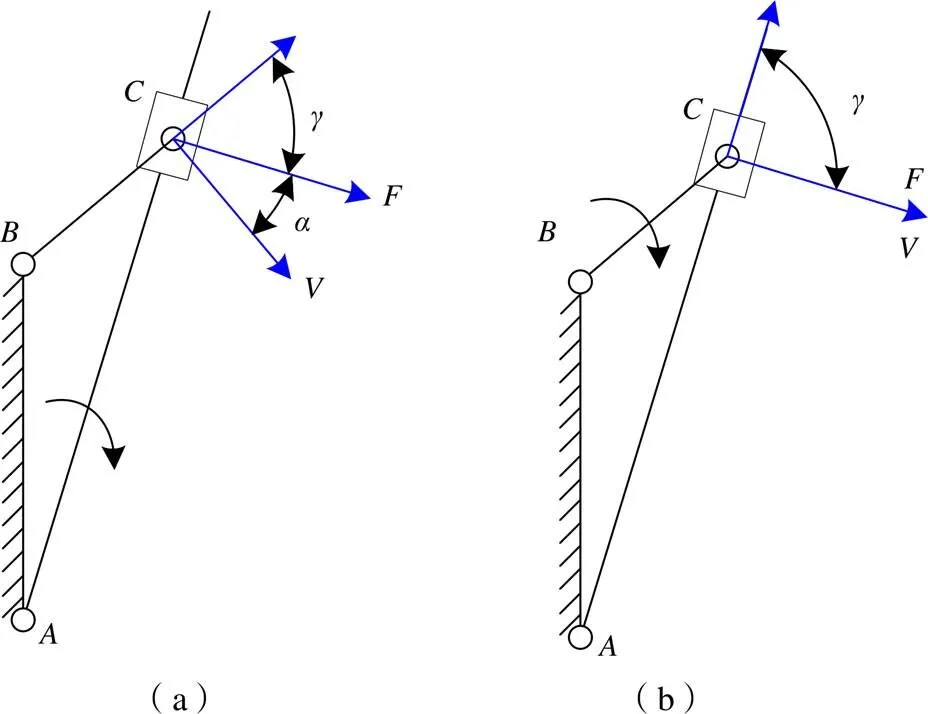
图4 导杆机构
通过上面的例子不难发现,按照新定义求解机构传动角时十分方便,只要将压力角和传动角分别列于从动件驱动力的两侧,所求的就是正确的传动角。这里需要指出的是,虽然上述方法是基于平面四杆机构推导出来的,但是该结论具有一般性,即可以适用于其他机构,如凸轮机构、齿轮机构等。
3.4 凸轮机构
图5为一凸轮机构,凸轮为主动件,尖端推杆为从动件。当凸轮逆时针绕转动时,推杆做往复直线运动。从动件驱动力方向为沿曲线过接触点的法向-,从动件速度方向沿杆,两者的夹角为凸轮机构的压力角。类似的,传动角如图5绘制时保证位于和之间。为便于解释说明,根据力学三角形法则将驱动力分解为水平分量2=cos及竖直分量1=sin,由于1和的方向一致,1对推杆做正功,为有效驱动分力,且越大,1越大,越利于推杆运动;而2垂直于方向,只产生挤压效果而做功为0,为无效驱动分力。因此,根据传动角的物理定义,为该凸轮机构的传动角。
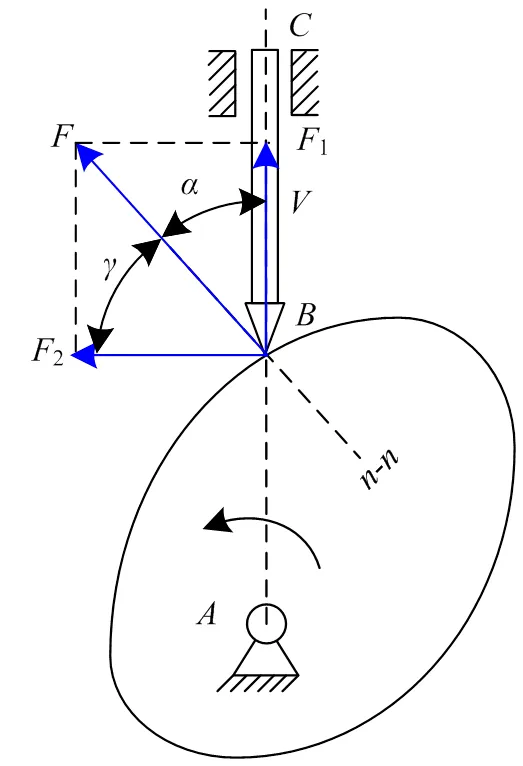
图5 凸轮机构
3.5 齿轮机构
图6为一齿轮机构,2为主动轮齿,1为从动轮齿,两者啮合于点。当2顺时针转动时,从动件1逆时针转动,且其驱动力沿接触处齿廓曲线的公法线-方向,从动件速度方向垂直于连线,两者间的夹角为压力角。为使位于和之间,传动角必须位于的下侧,如图6所示。根据力学三角形法则,将驱动力分解为分量1和2,其中1=sin为有效分力,2=cos为无效分力。且越大,1越大,绕点的转矩越大,越利于从动轮齿2运动,因而与其物理含义相一致,为该齿轮机构的传动角。
4 采用新方法求解平面连杆机构最小传动角
在生产中,不仅要求连杆机构能实现预定的运动规律,而且希望运转轻便,效率较高。因此在进行平面连杆机构的分析和设计时,通常的做法求找出最小传动角,通过将其最大化来保证机构的力传递性能和效率。下面以曲柄摇杆机构为例,说明最小传动角的求解方法。
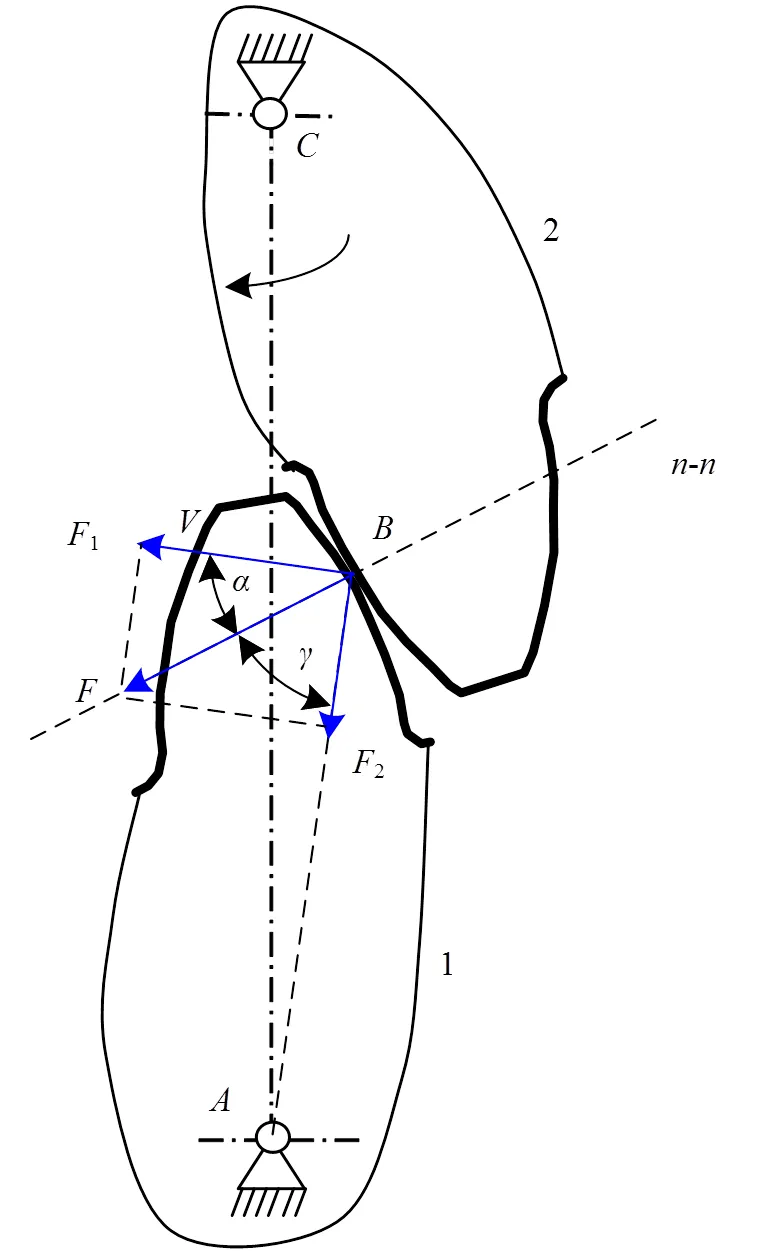
图6 齿轮机构
按照传统教材[3]用解析法求解机构的最小传动角min的位置时,不妨取任意时图7的刻曲柄摇杆机构所在位置,假设曲柄与水平轴的夹角为,根据教材定义可以画出压力角和传动角。可以看出此时Ð和传动角为对顶角,因此可以转而求Ð的数值间接求出的大小
对于△,根据余弦定理则有:
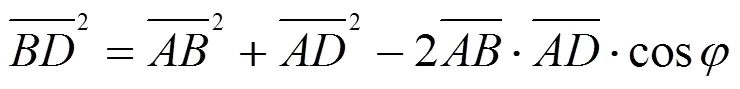
同理,对于△,有:

由此可得:
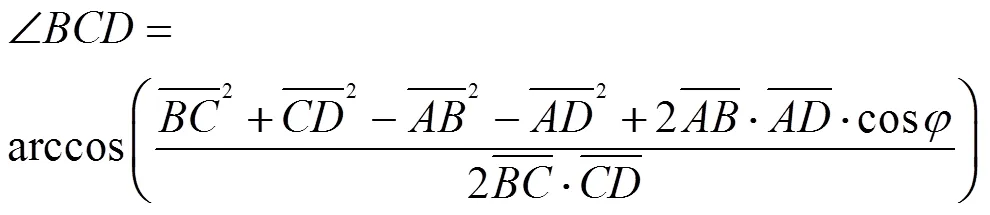
根据函数单调性可知,Ð是的增函数当曲柄转角=0°时,即杆位于1的位置时,得Ðmin;而根据传动角的定义可知,传动角为锐角。若Ð在锐角范围内变化,如图7所示,传动角=Ð,Ðmin为传动角极小值,即min=Ðmin;当曲柄转角=180°,即杆位于2的位置时,得Ðmax。若Ð在钝角范围内变化,传动角=180°-Ð,显然Ðmax为传动角的另一个极小值,即min=180°-Ðmax。综上所述,曲柄摇杆机构的最小传动角必然出现在曲柄与机架共现(=0°或=180°)的位置,即:

上述步骤为传统求解传动角的思路。由上面过程可以看出,如果按照传统解析法求解平面机构最小传动角时,需要始终“关注”Ð的变化趋势,且需要分锐角和钝角两种情况进行分别讨论,增加了分析求解的复杂性。此外,容易造成误解的是,Ð并不是传动角,Ðmin(或Ðmax)和最小传动角min也不可等同而言,它们只是数值上在一定几何关系(相等或互补)。因此,无法单纯地将“连杆和从动件之间所夹的锐角∠=称为传动角”。综上,传统教材的解析法只是给出了最小传动角的数值,而并未在结构简图中正确呈现最小传动角的位置关系。
当采用新途径求解最小传动角时,我们同样可以画出连杆机构在位置时压力角和传动角,如图8所示,通过观察可以进一步发现,在该位置时在驱动力的下侧在驱动力的上侧。根据二者的数值关系可知=90°-,越大,越小,机构传力越费劲,传动效率越低。且当从动杆逆时针转动时,呈现减小趋势呈现增大趋势。因此当曲柄位于1时,max=1,min=1为传动角最小值,如位置11所示。又因为和Ð为对顶角,因此min=Ðmin;另一方面,在该过程中,锐角逐渐向0靠拢此时若从动杆继续逆时针转动,应该变为负值。但是由于压力角的定义为锐角,因此严格来说压力角不能为负角度,反映在几何上可以解释为压力角“反向”了,从而导致和的位置关系发生变化体现为在上在下,如图中2位置所示。

图7 解析法求解连杆机构的最小传动角
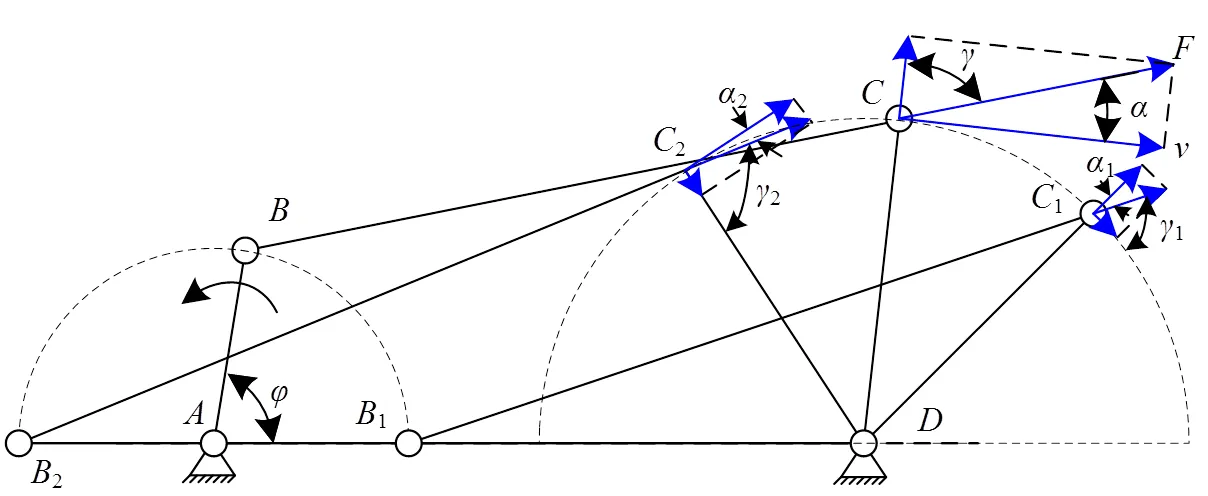
图8 新途径求解连杆机构的最小传动角
此时二者的数值关系为=90°-|,当从动杆持续逆时针转动时,|呈现增大趋势呈现减小趋势。且当曲柄位于2时,|max=1,min=2为传动角最小值,如位置22所示。
通过上述曲柄摇杆机构求解最小传动角的例子不难看出,借用新途径可以准确地求解机构在工作过程中的最小传动角,且可以较好地描述出压力角与传动角的位置关系。此外,既可以定量地给出min的具体数值,同时也能定性地反映出传动角角度的变化规律情况。
5 结语
本文从力学角度出发,分析了机构传动角提出的工程背景初衷及其物理含义,通过进一步补充说明改进了传统教材中传动角的定义,使得传动角的物理意义清晰且唯一,避免了使用时产生的歧义性与模糊性。通过图解法求解常见机构传动角的示例,表明了新定义的有效性与可靠性,同时该定义方法使用起来简单明了,易于被接受和理解。
[1]田福祥,刘晓斌,李洪民. 传动角理论的证伪[J]. 青岛建筑工程学院学报,1998(4):46-50.
[2]杨世明,金国光. 平面连杆机构平均传动角及其应用研究[J]. 机械,2008,35(5):19-22.
[3]杨可桢,程光蕴,李仲生,等. 机械设计基础[M]. 7版. 北京:高等教育出版社,2020.
[4]张建梅. 平面连杆机构传动角的浅论[J]. 科园月刊,2010(15):74-75.
[5]孙桓,陈作模,葛文杰. 机械原理[M]. 8版. 北京:高等教育出版社,2013.
[6]唐凌燕. 如何找出平面机构压力角和传动角[J]. 新课程(中),2012(8):64.
[7]杨光辉,滕弘飞. 机构传动角新定义[J]. 大连理工大学学报,2010,50(1):67-69.
[8]马超,熊晓航,王宏祥. 浅谈平面机构传动角教学方法[J]. 辽宁工业大学学报,2015(6): 133-135.
[9]张平历. 平面连杆机构压力角的教学策略[J]. 学园,2013(31):185-185.
[10]贲友国. 平面连杆机构压力角的教学策略[J]. 职业,2012(33):140-141.
[11]莫才颂. 平面连杆机构压力角与传动角引导式教学探索与实践[J]. 科技创新与生产力,2017,11(286):45-47.
On the Solution of the Transmission Angle of the Plane Mechanism from the Perspective of Mechanics
GAO Ge
(School of Mechanical Engineering, Jiangsu University of Science and Technology,Zhenjiang 212100, China)
The transmission angleis often used to judge the force transmission performance of planar mechanism. However, the definition of transmission angle is not given directly in the existing teaching materials. It depends on the solution of pressure angle, which produces ambiguity and makes it difficult for students to understand and use. This article aims at analyzing the actual physical meaning of the transmission angle from the perspective of mechanics. By introducing the concept of valid/invalid driving force, it gives the accurate definition of the transmission angle through supplementary explanations without changing the original definition in the teaching materials. Transmission angles of commonly used mechanisms are found through the new approach, which is simple and clear to ensure the uniqueness. What is more, how to find the solution of the minimum transmission angle via the new way is further discussed. Several examples verify that the definition is simple, clear and unique, which is easily accepted and used by students. It can help improve the corresponding basic concept in the mechanical design textbook.
transmission angle;pressure angle;mechanics
TH111
A
10.3969/j.issn.1006-0316.2022.08.002
1006-0316 (2022) 08-0006-07
2021-08-10
江苏省高等教育教学改革研究课题(2019JSJG532)
高阁(1988-),男,吉林桦甸人,博士,讲师,主要研究方向为结构拓扑优化设计,E-mail:gaoge@just.edu.cn。

