基于SPH-FEM算法的钢板接触爆破数值模拟研究

陈 诚，詹发民，周方毅，姜 涛

(海军潜艇学院，山东 青岛 266033)

1 引言

钢结构的接触爆破在工程爆破领域有着非常广泛的应用。由于爆破过程中产生的大变形、物质流动、界面接触等问题较为复杂，使用传统有限元法对此类问题进行数值模拟存在一定困难。目前对于钢结构接触爆破的数值模拟计算，通常采用ALE算法进行数值模拟计算，其优点是能够克服爆破过程中带来的网格畸变问题，计算准确度较高，能够较为准确地模拟炸药对钢板的破坏过程，ALE方法的缺点在于需要建立较大的空气网格，计算量较大，网格产生的大变形容易导致计算中止等。SPH算法是1977年由Lucy和Monaghan等人提出的一种无网格法，最初是用于解决天体运动问题，近年来被广泛用于爆炸效应的数值模拟计算。但由于SPH粒子的光滑长度一般取值较小，因此计算效率不高，且容易出现物质穿透、计算崩溃等问题。

为了综合FEM法与SPH算法的优点，提高计算效率及准确性，本文采用SPH-FEM耦合算法对钢板接触爆破过程进行数值模拟计算。基本方法是在炸药与钢板接触面附近变形较大的区域使用SPH粒子建模，钢板外围变形较小的区域采用FEM单元网格进行建模。这样既克服了FEM法导致的网格大变形问题，又能减少SPH粒子数量，提高计算的效率。

2 SPH算法基本理论

2.1 控制方程

SPH算法本质上是一种Lagrange法，因此其控制方程采用Lagrange形式的Navier-Stockes方程，通过三大守恒定律得到的

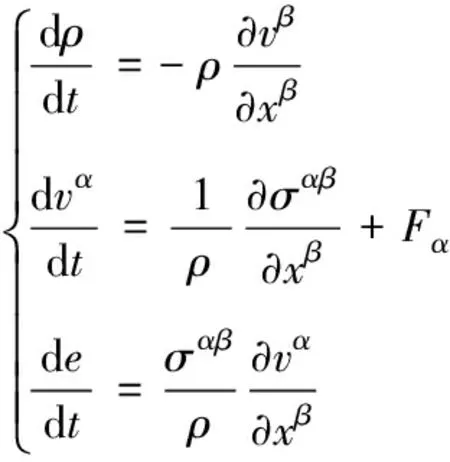
(1)

其中，，=1，2，3，代表坐标方向，遵循张量运算字母指标法；、、、、、、、表示密度、内能、速度分量、空间坐标、总应力张量和时间；表示作用在单位质量流体上的体力。

引入SPH的核近似和粒子近似原理，对式(1)进行粒子近似，得到用于爆炸数值模拟的离散化SPH控制方程

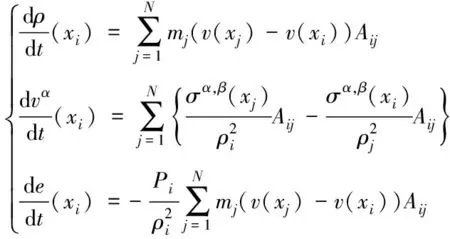
(2)

2.2 SPH粒子与FEM网格的耦合

对于SPH粒子与FEM网格的耦合，目前主流的方法有虚粒子法和罚函数法两种。虚粒子法虽然具有较高的精度，但是于对于复杂边界生成虚粒子困难，在某些情况下可能会发生粒子穿透边界；而罚函数方法容易实现，且能够处理复杂几何边界条件。

3 数值模拟计算模型

3.1 计算模型

数值模拟计算模型由炸药、离散为有限元单元网格的钢板和离散为SPH粒子的钢板三部分组成。炸药及钢板接触附近区域使用SPH粒子，外围钢板使用有限元网格。如图1所示，钢板尺寸为长40cm宽40cm厚度1cm；钢板中心20cm×20cm的区域离散为SPH粒子，粒子间隔0.5cm；钢板外围区域离散为尺寸为1cm的六面体有限元单元；200gTNT炸药尺寸为长10cm宽5cm厚度2.5cm，离散为SPH粒子，粒子间隔0.5cm。SPH粒子与有限元网格使用LS-DYNA中的*CONTACT-TIED-NODE-TO-SURFACE-OFFSET关键字进行耦合。

图1 SPH粒子与FEM网格的划分

3.2 材料模型及状态方程

炸药选用LS-DYNA材料库中的*MAT-HIGH-EXPLOSIVE-BURN材料进行模拟，炸药密度ρ=1.60g/cm，炸药爆速D=6930m/s，C-J压力P=27GPa。爆轰产物通过式(3)JWL状态方程进行描述，式(3)中、、、、为与炸药性质有关的常数。本例中取=374，=733，=415，=095，=030。

=(1-)-+(1-)-+

(3)

钢板采用*MAT＿JOHNSON＿COOK材料模型，钢板相关参数见表1，通过式(4)Gruneisen状态方程进行描述：

表1 钢板JOHNSON＿COOK模型相关参数

(+)

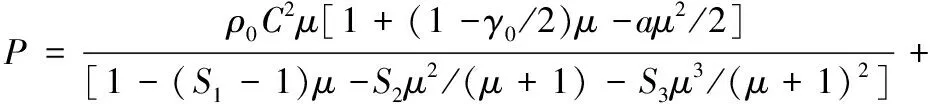
(4)

式(4)中：μ-μ曲线的截距C=1.4569；μ-μ曲线斜率的系数S=1.49、S=-0、S=0；Gruneisen参数γ=2.17；一阶体积修正量a=0.46；μ=(ρ/ρ)-1。

3.3 计算结果及分析

因炸药20后爆轰完全，对计算影响较少，为避免炸药的粒子出现速度超范围的情况，设置炸药粒子失效时间为20，设置总体计算时间为120。计算完成后使用后处理软件查看计算结果。

图2为20时的计算结果，从图中能够明显看出炸药爆轰过程和爆轰产物的飞散，以及钢板产生形变的过程。数值模拟计算结果显示爆炸发生后，爆轰产物与钢板接触后，钢板首先发生凹陷，当达到屈服极限后，钢板背面发生脱落。图3为120时的计算结果，可见钢板中心15×8的区域范围内产生凹痕，12×6区域范围内的产生脱落穿孔。

图2 20μs时炸药爆轰及钢板变形效果

图3 120μs时钢板的凹痕及穿孔

为了验证粒子与网格的耦合效果，选取接触面附近相邻的一个粒子和单元(本文选取2512粒子和10864单元)，导出其轴方向上的速度时程曲线如图4所示。对比压力曲线发现其波形及峰值大致相同，说明该处粒子将压力等物理量传递给了网格，耦合效果较好，进一步说明了-耦合算法的有效性。

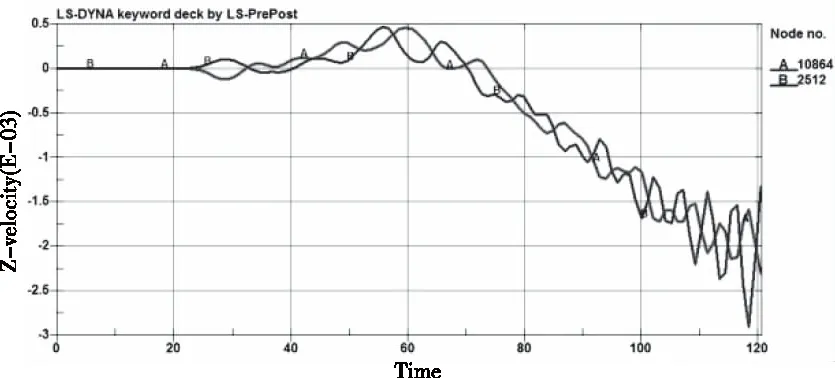
图4 SPH粒子与FEM网格z轴方向速度对比

3.4 SPH-FEM耦合算法与FEM算法计算效果对比

为了比较-耦合算法与单纯算法的优劣性，使用纯法建立有限元模型，通过算法进行求解。有限元模型与31节中计算模型尺寸相同，在钢板内外建立30厚空气层。炸药及空气使用网格，钢板使用网格。材料模型及本构方程与32节中相同。图5为两种算法计算效果的对比，可以看出，两种算法都能模拟出炸药对钢板的破坏过程。在钢板相同位置选取观测点，导出其压力时程曲线，本文选取钢板上坐标为(15，0，0)的点为观测点，图6为两个观测点的压力时程曲线，从曲线可以得出-耦合算法得到的观测点峰值压力为0151，而纯法得到的观测点峰值压力为0143，误差在5左右，计算结果较为接近。从计算时间上看，建立单纯网格，使用算法求解的计算时间为687秒，而-耦合算法计算时间仅为11秒，由此可见-耦合算法大大节省了算力，提高了计算效率。

图5 120μs时两种算法计算结果

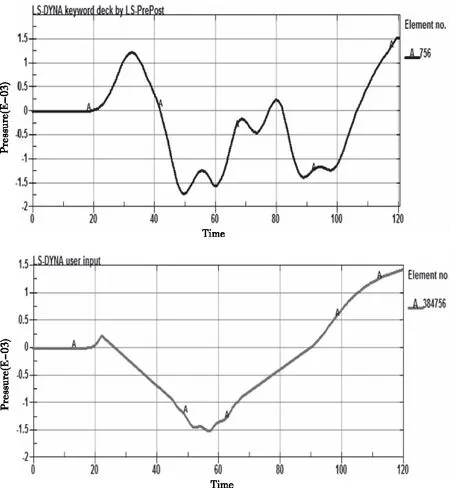
图6 钢板相同位置单元的压力时程曲线

4 试验验证

4.1 试验工况布置

为了验证-耦合算法的准确性，设计全尺寸接触爆破试验。如图5所示，钢板选用235普通碳素结构钢，平放于地面上。200药块置于钢板中心，用胶带进行固定，钢板背面设置厚度为30的临空面，使用8号雷管起爆，起爆点位于药块左端中心的雷管室。

图7 装药设置

4.2 试验效果及分析

爆破后效果如图8所示，在爆炸作用下，钢板产生穿孔，边缘产生凹痕。经测量，钢板中心产生10×5的穿孔，12×8区域产生明显的凹痕，与数值模拟计算结果吻合较好，验证了该算法的准确性。

图8 爆破效果与数值模拟结果对比

5 结论

-耦合算法能够基本模拟钢板接触爆破中的炸药爆轰、压力传递，钢板形变等过程，计算准确度较高，与单纯法相比，-耦合算法因无需划分复杂网格，大大减少了计算复杂度，提高了计算效率。-耦合算法实施的关键点是粒子与网格的耦合，本文采取罚函数法进行处理，对粒子和单元接触面进行接触定义。通过试验验证，-耦合算法能够成功应用在钢板接触爆破中。