非饱和黄土弹性模量与饱和度关系模型研究
郑 洁,郑红卫,王菁莪
(1.武汉工程科技学院 信息工程学院,武汉 430200; 2.中国地质大学(武汉) 教育部长江三峡库区地质灾害研究中心,武汉 430074)
1 研究背景
模量是描述材料应力与应变关系的重要参数,表征材料在外力作用下抵抗变形的能力。在材料弹性变形阶段,应力和应变关系符合胡克定律,二者呈正比例关系,其比例系数称为弹性模量。在岩土材料应力应变分析和研究中,弹性模量是必不可少的基础参数,如岩土材料应力-应变本构模型的建立[1-2],以及岩土体变形理论计算和数值模拟分析等[3-4]。弹性模量的概念源自连续介质力学领域,用于表征材料抵抗外力造成弹性变形的能力。对于饱和土,造成土体变形的应力为通过内部土颗粒传播的有效应力,可通过总应力与孔隙水压力计算。在岩土力学领域,弹性模量的物理意义实质为岩土材料在有效应力作用下抵抗变形的能力。对于非饱和土,有效应力理论研究成果众多,如双应力变量理论、广义吸力理论,以及吸应力理论等[5-8]。非饱和土的弹性模量不仅受应力水平控制,而且与含水率及吸力相关[9],其本构模型大部分建立在考虑含水率或基质吸力的基础之上[10-12]。
目前关于非饱和土弹性模量与本构关系的理论研究成果众多,但在测试方面,仍局限于传统的单轴或三轴压缩试验方法。岩土材料弹性变形阶段的变形相对较小,对测量设备的应力控制精度与变形测量精度有较高的要求。随着计算机图像识别与处理技术的发展,基于数码图像处理的方法开始被用于岩土变形的高精度测量[13-15]。
本文尝试使用基于非饱和土有效应力理论与计算机图像处理技术相结合的方法测试和分析典型非饱和重塑黄土弹性模量随含水率的变化特征,旨在为非饱和土弹性模量测试方法和理论研究提供参考。
2 试验材料
黄土是我国西北、华北和黄土高原地区广泛分布的一种特殊土。受干旱、半干旱气候条件影响,该区域的黄土常处于非饱和状态。非饱和黄土在干湿循环过程中表现出的湿陷性与强度大幅度降低等特殊物理力学性质是工程建设的主要工程地质问题[16-17]。我国“一带一路”沿线经济带大部分区域不同程度穿过黄土地区,西气东输、西电东送、高速铁路与高速公路网建设等国家重大工程项目也与黄土地区密切相关。因此,开展非饱和黄土工程性质研究对国家重大工程建设与经济发展具有重要的意义。本文依托西气东输工程管道黄土地基稳定性相关科研项目,针对非饱和黄土弹性模量与饱和度关系开展研究。
本次试验样品为陕西省子长县西气东输管道典型地基马兰黄土,通过室内土工试验测得原状土样的天然含水率和天然密度分别为20.8%、1.46 g/cm3,液限为30.2%,塑性指数为11,颗粒相对密度为2.72。为避免黄土结构不均匀性的影响,本次试验采用重塑土样开展。取回的原状黄土充分搅拌混合均匀后,制成干密度分别为1.5、1.6、1.7 g/cm3的3种不同密实程度重塑土样(编号分别为试样1、试样2与试样3)。样品形状为底面直径61.8 mm、高10 mm的圆柱状土饼。每种干密度试样各制3个,分别用于土水特征曲线测试、泊松比测试,以及自然风干过程的变形与含水率测试。
3 试验仪器与方法
3.1 试验仪器
试验所使用的仪器主要包括压力板仪、单轴压缩仪与自主研制的多功能摄影测量装置。其中,压力板仪用于测量土样的土水特征曲线,单轴压缩仪用于测量样品的泊松比。多功能摄影测量装置结构示意如图1所示,该装置包括摄影棚、数码相机与电子秤3个主要组成部分。其中,摄影棚为边长40 cm的立方体不透光空间,内部安装有LED白光源。数码相机通过支架安装在摄影棚顶部中心位置,可通过控制程序定时获取样品图像。电子秤质量分辨率为0.01 g,可实时输出质量测量数据。待测试的饼状土样平放于电子秤的称量盘上,土样和称量盘之间涂有一层凡士林,用于消除样品与称量盘之间的摩擦力,使样品在自然风干过程中尽量均匀收缩变形,避免产生裂缝。

图1 摄影测量装置示意图Fig.1 Schematic diagram of photogrammetric device
3.2 试验步骤
(1) 使用真空饱和器将试样饱和,称量样品饱和质量,结合试样的干密度与体积参数,计算样品的饱和体积含水率。
(2) 将3种干密度的饱和试样各取一个先后装入单轴压缩仪,控制竖向压力分别为5、10、20、30、40、50、60、70 N,同时测量样品变形稳定后的垂直与水平向变形数据,根据水平向应变与竖向应变的比值计算泊松比。
(3) 将3种干密度的饱和试样各取一个同时放入压力板仪。控制压力板仪气压分别为3、7、10、25、50、100、200、300、400、500 kPa,称量各级压力下土样排水稳定后的质量数据,拟合土水特征曲线。
(4) 将3种干密度的饱和试样各取一个先后放在摄影测量装置的称量盘上(涂有凡士林),设置照相机间隔拍照时间为10 min,同时记录拍照时电子天平质量读数,直至样品质量变化<0.01 g/h停止试验。
3.3 数据处理
试验数据处理过程包含应变计算、应力计算与弹性模量计算3个主要步骤。试样在自然风干过程中的变形通过基于计算机图像处理的粒子图像测速方法(PIV)获得。如图2所示,土样在t1时刻初始状态的数码图像被划分为若干正方形单元格(图2(a)),同时计算各单元格中心点的像素坐标,像素坐标通过照相机标定参数可换算为实际距离坐标。实际试验中,土样图像被划分为1 600个单元格。随着土样自然风干失水,在t2时刻,含水率由θ1降低为θ2,土样发生收缩(见图2(b)),各单元格发生移动与变形,如单元A经移动和变形为单元A′。PIV程序通过快速傅里叶变换搜索和评价变形前后图像各单元格的相关性,逐像素找出匹配度最高的单元格,并计算变形后单元格的坐标(如图2(c))。重复上述流程即可获得土样所有单元格变形前后的坐标[14]。

图2 PIV方法原理示意图Fig.2 Schematic diagram of principle of PIV method
尽管重塑土样被尽量混合均匀,但仍然会存在一定的不均匀性,造成饼状样品在风干收缩过程中的收缩中心并不与其形心一致,而是在平面上不规则运动。
图3显示了试样轮廓、收缩中心点,以及3个典型单元格变形前后位置示意。由于越靠近收缩中心点的单元格移动距离越小,因此可通过各单元格变形前后的坐标之差计算收缩中心点的位置。通过收缩中心点与各单元格中心点变形前后的坐标,可计算各单元格中心点的位移u,以及距收缩中心点的距离r,其应变ε即为u与r的比值。

图3 试样失水收缩变形示意图Fig.3 Schematic diagram of the shrinking process of sample during drying
土样在风干失水收缩过程中各点的受力状态可通过图4所示的以极坐标形式表示的线弹性平面应力单元受力状态分析[13]。单元的应力-应变关系可表示为式(1)所示。
(1)
式中:εr为指向收缩中心的径向应变;εβ为环向应变;γrβ为单元旋转应变;E为弹性模量;σr′和σβ′ 分别为径向和环向有效主应力;τrβ为剪应力;υ为泊松比。

图4 单元受力状态示意图Fig.4 Stress state of element
对于底部无摩擦、顶面和侧面无附加应力的饼状试样,在自然风干过程中仅受由基质吸力引起的内部有效应力作用,即吸应力σs,且吸应力各向同性分布于土样内部[6]。因此,试样内各点的径向和环向有效主应力与吸应力相等,无剪应力,各点仅发生指向收缩中心的变形,即
(2)
考虑到非饱和土的吸应力与弹性模量随含水率变化,不同含水率状态下的弹性模量可写为
(3)
式中:E(θ)和σs(θ)分别为试样在体积含水率为θ时的弹性模量与吸应力。
其中,试样不同含水率状态下的吸应力可基于土水特征曲线VG模型拟合参数计算[18-19],即
(4)
(5)
式中:α和n为土水特征曲线VG模型拟合参数;Ψ(θ)为试样体积含水率为θ时的基质吸力;θs和θr分别为饱和体积含水率与残余体积含水率。
基于PIV图像处理方法获取的试样各单元格中点变形数据、土水特征曲线拟合参数,以及含水率与泊松比测试数据,通过式(3)至式(5)即可分别计算试样1 600个单元格区域在各含水率状态下的局部弹性模量。鉴于土样仍存在一定的不均匀性,不同局部区域的弹性模量略有差异,通过求平均值即可获得可代表试样整体的弹性模量。
4 试验结果与讨论
4.1 泊松比
不同干密度样品的泊松比测试结果如图5所示。将不同竖向压力条件下,横向应变与竖向应变离散测试数据进行线性拟合,得出干密度1.5、1.6、1.7 g/cm3的试样泊松比分别为0.264、0.280、0.319,其值随干密度增大而增大。试样的泊松比均在饱和状态下测得,本文暂未考虑泊松比可能随含水率变化的情况。

图5 泊松比试验结果Fig.5 Test result of Poisson’s ratio
4.2 土水特征曲线与吸应力特征曲线
通过土水特征曲线VG模型(式(4))将由压力板仪测得的含水率与基质吸力离散数据进行拟合,可得到如图6(a)所示的不同干密度试样的连续土水特征曲线(压力板试验样品体积变化量<0.6%,质量含水率与体积含水率换算误差较小,在此忽略不计)。通过式(5)计算得不同干密度试样的吸应力特征曲线与模型拟合参数如图6(b)所示。
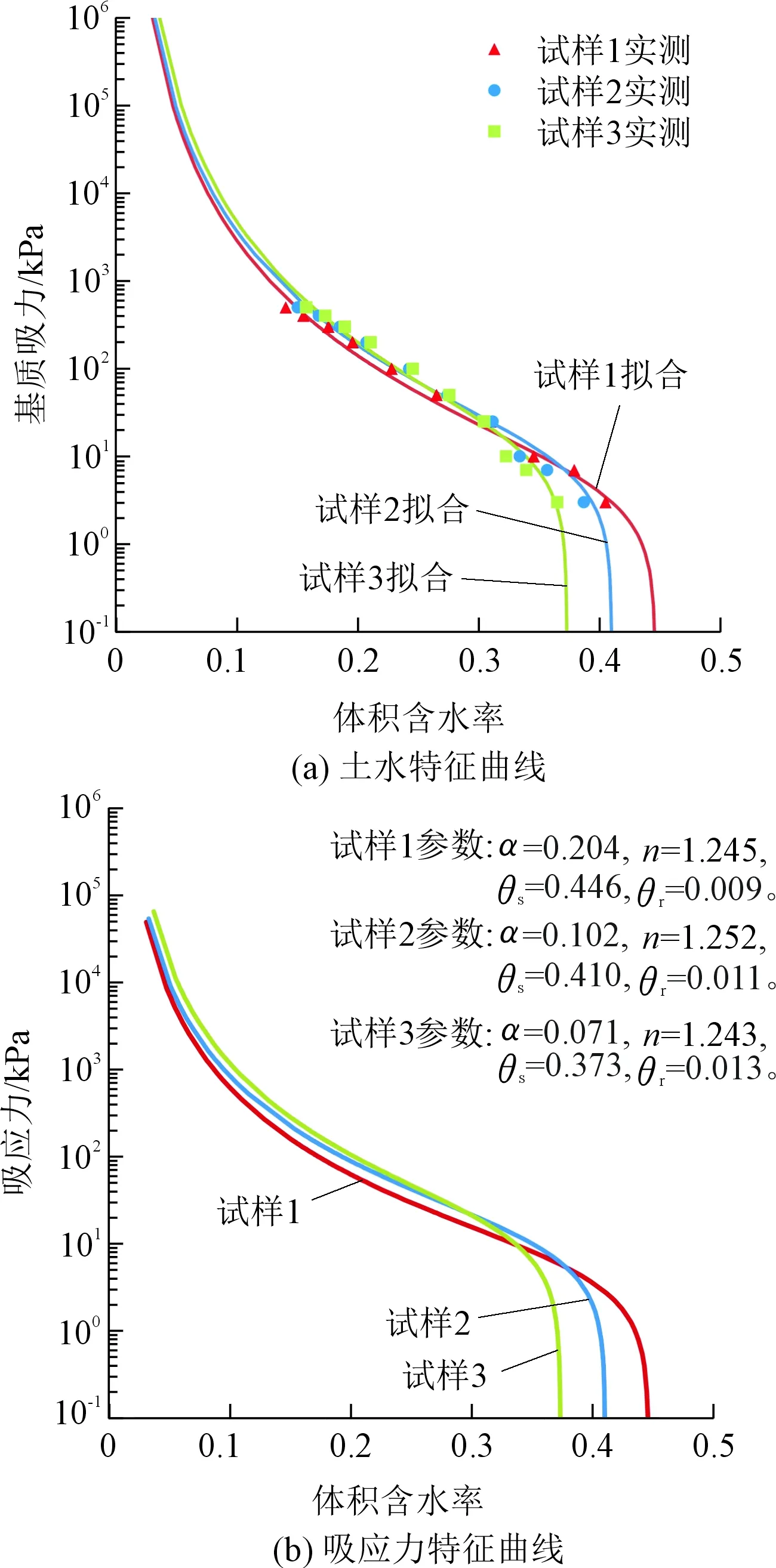
图6 试样土水特征曲线和吸应力特征曲线Fig.6 Soil-water characteristic curves and suction stress characteristic curves of samples
基质吸力反映非饱和土中孔隙水的能量状态,其数值上等于孔隙气压与孔隙水压之差,并不能全部转化为有效应力[6]。通过连续的吸应力特征曲线可计算试样任意含水率状态时的吸应力,即有效应力,为后续弹性模量计算提供数据。
4.3 变形过程
将试样自然风干过程中不同含水率状态下的图像与初始饱和状态图像对比,通过PIV程序可计算各单元格中心点位移矢量数据。以干密度1.6 g/cm3的试样为例,图7显示了该试样体积含水率分别为0.397、0.363、0.276、0.192时的图像,以及相应的最大位移。图7中白色点为收缩中心点,箭头表示各单元格的位移与移动方向。受土样局部密度与摩擦力差异影响,土样不同时刻的收缩中心点位置略有移动,但中心点附近单元格位移最小,距离该点越远变形越大。基于收缩中心点不同时刻的实际坐标值,土样各单元格局部的应变计算可消除收缩中心点移动的影响。

图7 试样2干缩过程图像Fig.7 Image of sample 2 during drying and shrinking
4.4 弹性模量计算与分析
基于上述试样在不同含水率状态时的吸应力与应变数据,各单元格局部的弹性模量通过式(3)计算。同样,以干密度1.6 g/cm3的试样为例,图8显示了该试样在含水率0.276时各单元格局部弹性模量计算结果散点图。由图8可见,试样不同区域弹性模量大部分集中分布于4~7 MPa之间,但仍有少数单元格计算结果偏差较大,特别是与收缩中心点比较靠近的区域。其主要原因是收缩中心点附近区域在风干失水过程中变形相对较小,应变测量存在较大的误差。为了获得试样整体的代表性弹性模量,将明显偏差较大的单元格计算结果剔除(如图8两条虚线以外的数据),然后计算剩余单元格弹性模量计算结果的平均值(如图8实线所示),作为该试样在当前含水率状态下的代表性弹性模量。通过该方法,计算得3种不同干密度试样在不同饱和度时的弹性模量与饱和度关系曲线如图9所示。
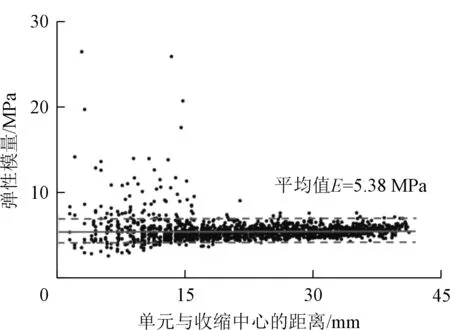
图8 试样2弹性模量计算结果散点图Fig.8 Scatterplot of elastic modulus of sample 2

图9 试样弹性模量与饱和度关系曲线Fig.9 Relation curves between elastic modulus and saturation of samples
通过Levenberg-Marquardt算法对数据进行拟合,得出式(6)在实测数据范围内可较好地拟合试样弹性模量与饱和度之间的关系,拟合参数见表1。
E=a-bcSat。
(6)
式中:E为弹性模量;Sat为饱和度;a、b、c为模型拟合参数。

表1 弹性模量与饱和度关系模型拟合参数
从上述试验结果可以看出,各试样弹性模量随饱和度降低呈指数增大,且随着初始干密度的增大,弹性模量随饱和度变化的幅度越大。
上述现象的物理机制包括两个方面:其一,土体在含水率降低过程中,基质吸力与吸应力增大,从而提高了土体内有效应力,使土颗粒之间摩擦力增大,抗变形能力提高,其宏观表现为弹性模量增大;其二,土体在风干失水过程中发生体积收缩,使土体密实度增大,可压缩性降低。本文所述试验方法所获取的弹性模量变化是上述两种机制综合作用的结果。已有文献[9,20]基于试验与推导所得的非饱和土弹性模量与含水率的关系同样表现为指数函数关系,与本文结论一致。
试验数据显示,3种干密度的非饱和马兰黄土样品的弹性模量在饱和状态时为300~900 kPa,而当饱和度降低至40%~50%时,其弹性模量骤然增大数十倍,可见饱和度对土体抗变形能力的影响显著。通过式(6)所示的模型可以较好地拟合弹性模量与饱和度之间的函数关系,该模型对已有测试数据的拟合优度R2均超过0.99。
在实际应用中,先通过本文所述的测试方法获取多个饱和度状态下相应弹性模量的离散数据,然后通过上述数学模型将离散数据拟合为连续数据曲线,即可获取试验区间内任意饱和度状态下的弹性模量,可为黄土工程性质分析评价与工程设计施工提供基础数据。
5 结 论
(1)提出了一种基于吸应力理论与PIV技术相结合的非饱和土弹性模量测试方法。该方法通过多功能摄影测量装置获取饼状土样从饱和状态到自然风干过程中的高分辨率数码图像与含水率变化数据。结合土水特征曲线、泊松比等测试数据,基于吸应力理论计算获取土样在不同饱和度或不同含水率状态下的弹性模量。
(2)通过该方法对干密度分别为1.5、1.6、1.7 g/cm3的重塑马兰黄土试样进行测试,得出土样弹性模量随饱和度降低而呈指数增大。试样干密度越大,其弹性模量随饱和度降低而增大的幅度越大。提出了拟合非饱和黄土弹性模量与饱和度关系的3参数指数数学模型,该模型表达式可较好地拟合已有测试数据。
(3)基于PIV高精度数码图像处理方法可以准确获取非饱和土含水率变化过程中的微小变形数据。将该技术与非饱和土有效应力理论相结合,为非饱和土弹性模量测试提供了新的试验思路。使用该方法可快速低成本地获取黄土样品多个饱和度状态下的弹性模量,然后通过数学模型拟合获取连续的弹性模量与饱和度关系曲线。上述测试方法与数学模型可为非饱和土测试仪器的研发,应力、应变性质的研究与工程应用提供参考。

