Probing subcycle spectral structures and dynamics of high-order harmonic generation in crystals

Long Lin(林龙) Tong-Gang Jia(贾铜钢) Zhi-Bin Wang(王志斌) and Peng-Cheng Li(李鹏程)

1Research Center for Advanced Optics and Photoelectronics,Department of Physics,College of Science,Shantou University,Shantou 515063,China

2Key Laboratory of Intelligent Manufacturing Technology of MOE,Shantou University,Shantou 515063,China

3College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,China

Keywords: high-order harmonic generation,carrier dynamics,subcycle laser pulses,crystal systems

1. Introduction

High-order harmonic generation (HHG) caused by the intense ultrafast laser fields[1-7]has been one of the hottest topics in modern ultrafast physics since one of the promising methods for generation of attosecond pulses. The structural and electronic dynamic information of a system is carried by the HHG spectra and momentum spectroscopy,[8-10]which have a very important application in direct imaging material structure and electronic trajectory.[11,12]In particular,the HHG in crystals is a subject of much current interest,which is related to new phenomena and electron dynamics.[13-17]Since the experimental observation of non-perturbative crystal harmonics passed through lasers operating in the mid-infrared(MIR) scale,[18]the emergence of HHG in crystals has attracted extensive attention in the field of attosecond science.Extending the success of attosecond metrology in the gas phase to crystal systems can help us to obtain new compact ultrafast light sources.[19-23]The harmonic generation mechanism in crystals is different from the gas phase owing to the high density and periodicity of crystals.[18]

Currently, there are more and more fundamental studies about HHG in crystals. The experiments by Schubertet al.[24]have proved that subcycle electron dynamics play an important role in the crystal-state harmonic generation by revealing the carrier-envelope phase dependence in the harmonic spectrum of GaSe crystal driven by strong field of 30 THz. Vampaet al.[25]have proposed a method to apply gas-phase highharmonic spectroscopy to crystals, which can be explained by classical trajectory analysis. The effects of impurities and scattering of harmonic generation in crystals have been investigated by Kemperet al.[26]Fuet al.[27]theoretically investigated the dynamic processes of solid harmonics generation using the one-dimensional time-dependent density functional theory. To date,it is generally accepted that the HHG in crystals is contributed by two distinct mechanisms:intra-band current and inter-band polarization. Wuet al.[28]have explained in detail that the multi-plateau structures of HHG in crystals are related to these mechanisms. Liet al.[29]have studied the enhancement of the second plateau in solid high-order harmonic spectra by two-color fields. The inter-band transitions are analogous to the three-step model in gas HHG. To gain insight into the physical dynamics underlying extreme ultraviolet(XUV)emission in experiments, Luuet al.[19]have conducted both semiclassical mechanical simulations and verified the consistency of the single-band model to experimental results.Their results have proved that the laser-driven intra-band current can accurately capture the XUV emission. In addition,it constitutes the first measurement of the fine details of the conduction band dispersion in wide band-gap materials. The study of dielectric materials,especially wide bandgap materials, has broad theoretical and application prospects. Chenetal.[30]have investigated probing dynamic information and spatial structure of Rydberg wave packets by harmonic spectra in a few-cycle laser pulse. They explained the harmonic spectra with a periodic variation, which directly illustrates the electron oscillation between the two neighboring Rydberg states by controlling the time delay of pump-probe laser pulses.

Because of the carrier motion in crystals,which can make almost the instantaneous response to the perturbing laser field,subcycle spectral structures and dynamics of HHG processes can be uncovered by probing the transient changes of the carrier by adding the few-cycle laser pulses to the fundamental laser field. The subcycle HHG is theoretically very well understood in atom[31-35]and molecule systems. Chiniet al.[32]have studied the subcycle AC stark shifts in helium atoms on the attosecond time scale. Subcycle dynamics have been revealed by Bell and Chen,[33]who have carried out the transient absorption XUV spectroscopy experiments on helium in the presence of near-infrared laser fields.Considering the electron correlation,electronic dynamical response and laser polarization effects,Heslaret al.[34,35]have analyzed the several subcycle dynamical behaviors of the energy level spectrum and fine structures of the photoemission line patterns in two-color two-photon processes. However, the HHG in crystals driven by the subcycle laser pulses is less understood. The goal of this work is to understand the subcycle spectral structure and dynamical process of the HHG in crystals. Here, we adopt Luu’s model for probing subcycle spectral structures and dynamics of intra-band HHG in crystals. The same scheme has been extended for probing the oscillation structures of multiband from the practically mixed intra- and inter-band crystalline HHG spectrum based on Bloch state basis.[36]HHG in crystals creates a new methodology to understand all-optical spectroscopy of the current carrier structure and dynamics in crystals.

In this paper, we present the HHG spectra of crystals in MIR laser fields and the few-cycle femtosecond laser pulse with a time delay. The HHG spectra of crystals are calculated by solving the Boltzmann equation in crystal momentum space for the intra-band carrier dynamics and the time-dependent Schr¨odinger equation (TDSE) based on Bloch state basis in velocity gauge for the treatment of multi-band crystal systems.From the HHG spectra as a function of time delay, it is seen that oscillation structures are similar to both single-band and multi-band crystal systems,but it is different from the atomic and molecular systems. Combining the spectral and temporal spectra and the probability density distribution of the radiation in crystal momentum space, subcycle spectral structures, and dynamics of the HHG in crystals are clarified.

2. Theoretical methods

2.1. Single-band model

The HHG spectra can be obtained by performing a calculation of the Boltzmann equation in crystal momentum space for the intra-band carrier dynamics and the TDSE based on Bloch state basis in velocity gauge for the treatment of multiband crystal systems,respectively.

For the one-dimensional single-band model,[37]the Boltzmann equation related to the time evolution of the population distributionf(k,t)can be written as

wheref(kc,t)is a population of the particle at crystal momentumkc,qis the charge of the particle,andE(t)is the electric field.In this model,the electron is assumed to be excited to the conduction band of the lowest energy at the beginning of the pulse and moves within the same band without further excitation to higher conduction bands or de-excitation to lower valence bands. Despite its simplicity,this model has been shown to give HHG power spectrum that is comparable to experimental results.[19]It is feasible that this model is selected as the basis for subcycle intra-conduction band dynamics of further study of HHG in crystals. We assume that the external fields are polarized in the same direction. The laser fields can be written as

The dispersion relation is generally expanded in the Fourier series. For general symmetric band structure, the band structureε(kc)is assumed to be symmetric about the origin at the crystal momentumkc=0 andε(kc)=ε(-kc), it can be expressed as

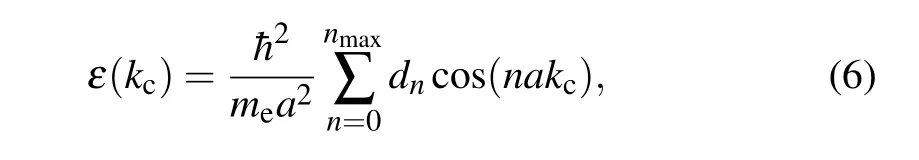
wheremeis the effective mass of the particle in the singleband,ais the lattice constant, anddnis the expansion coefficient of thenth component. We set the first Brillouin zone

In the frequency domain,this relation can be rewritten as[38]

2.2. Multi-band model

For multi-band crystal systems, the TDSE in velocity gauge is employed based on the Bloch state basis[39]for an electron interacting with a periodic potential as follows:

3. Results and discussions

3.1. Laser-induced intra-band HHG oscillation structures

3.1.1. Spectral and temporal features of oscillation structures

It is well known that the experimental studies of subcycle AC Stark shifts in atoms have been reported.[30,40-42]To a comprehensive understanding of subcycle spectral structures and dynamics of HHG processes in crystals, one advantage of studying is firstly an exploration of the intra-band carrier contributions. The Boltzmann equation provides complementary information to identify intra-band dynamics of the crystals. Although the Boltzmann equation is at best qualitative,its single-band carrier dynamics provides a clearer physical picture for the HHG in crystals. To understand the generation of HHG oscillation structures in crystals driven by an MIR and subcycle laser pulse with a time delay,Fig.1 presents the corresponding scheme. It is clearly seen that the oscillatory pattern in HHG spectra becomes much more complex in comparison with the atomic case.[32,34,35,40]

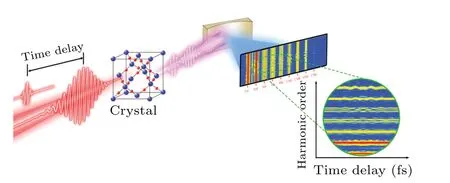
Fig.1.Schemes of the generation of HHG oscillation structures in crystals driven by the MIR and subcycle laser pulse with a time delay.

Figure 2 presents the oscillating pattern of the HHG of the crystal SiO2driven by the MIR laser fields subject to excitation by a subcycle laser pulse. There are obvious shifts between odd orders and various oscillating structures. As shown in this figure,we have selected two regions where the oscillation structures are quite regular and marked with red dashed circles. In order to further analyze the oscillation structures,we have also selected some relatively representative time delays as shown in Fig. 3. In calculation, we consider a onedimensional model of the first conduction band of SiO2with lattice constant along withΓ-Mequal to 0.491 nm. The conduction band structureε(kc)is symmetric concerning the zero crystal momentumkc=0 and is expanded as a Fourier cosine series by Eq. (6). The significant Fourier expansion coefficients of this conduction band up to the 5th mode ared0=10.6,d1=-1.669,d2=0.0253,d3=-0.0098,d4=0.0016,andd5=0.0263,with all in units of eV.We set the wavelengthλ1of the MIR pulse as 2533.1 nm, the duration of the laser pulse is 80.3 fs with a cos2envelope. The 2533.1 nm has been chosen for probing subcycle spectral structures and dynamics of intra-band HHG in crystals based on the model band structure we selected. The wavelengthλ2of the probing pulse is 3800 nm with a 13.8-fs full width at half maximum(FWHM),which just is one third of the energy range of the single-band model. The laser intensities used areI1=1×1012W/cm2andI2=1×1010W/cm2, respectively.I1andI2are obtained by|E01|2and|E02|2as shown in Eqs.(3)and(4). In our calculation, the laser intensity is chosen based on the pervious theoretical or experimental studies.[28]The HHG is calculated as a function of the time delay between two laser pulses,it allows us to understand the carrier dynamics of the HHG in crystals.Here the time delaytdis in the range-40 fs≤td≤40 fs.For the intra-band HHG,the carrier moves under the action of the laser field,producing intra-band current and photons emission. The result shows that the oscillating pattern of the HHG becomes more complex in crystals.

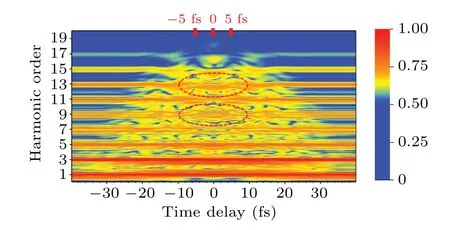
Fig. 2. HHG spectra from SiO2 as a function of the time delay between MIR and subcycle laser pulses. The red dashed lines indicate the regions of the oscillating pattern.

To further analyze subcycle intra-conduction band dynamics of HHG in crystals, the specific time delaytdis selected to further investigate the underlying physical mechanisms of these oscillations. We present the HHG spectra with three specific time delays attd=-5 fs,td=0 fs,andtd=5 fs marked by the red arrows as shown in Fig.2. The results are shown in Fig.3. It can be seen that the harmonic spectrum under the monochromatic mid-infrared laser field also has multiple sub-peaks. The reason is that the energy band oscillates with the time-dependent laser field, leading to a temporally changing band structure called the subband.[43]The excitations between the band and subband are responsible for the generation of multiple sub-peaks of harmonic spectra. This phenomenon is similar to the role of the dressed state in the atomic systems. Thus, multiple sub-peaks are generated either MIR-subcycle laser or MIR alone, especially the region of the plateau. It is obvious that HHG spectra have a shift with various time delays.

Fig.3. HHG spectra in MIR and subcycle laser pulses at three specific time delays with td =-5 fs,td =0 fs, and td =5 fs, respectively. For comparison, the HHG spectra of the crystal driven by the MIR laser pulse alone are presented as the black dashed line.

To explore the detailed spectral and temporal features of the HHG oscillation structures from crystals, we perform the time-frequency analysis by means of the wavelet transform of the currentJ(t):

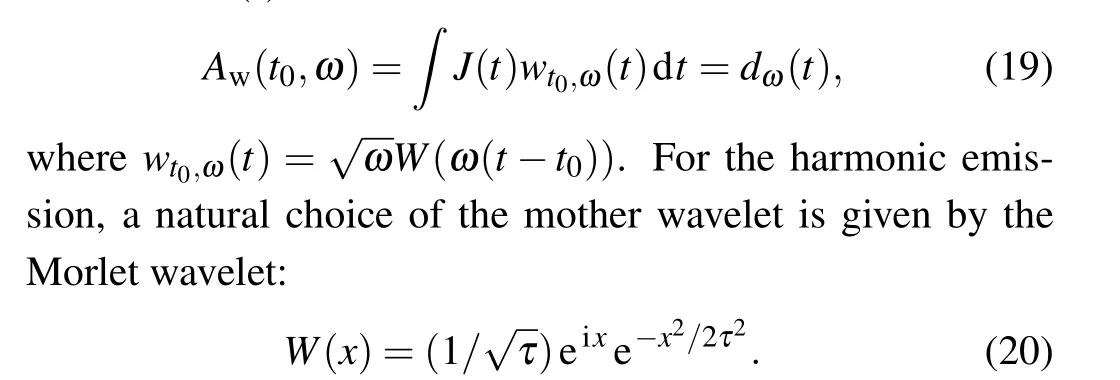
We chooseτ= 15 to perform the wavelet transform. Figures 4(a), 4(b), and 4(c) show the time-frequency spectra of the current in crystals at time delaytd=-5 fs,td=0 fs,andtd=5 fs,respectively. These results reveal striking details of the spectral and temporal structures. As illustrated in this figure,the symmetry of the emission spectra is broken when the time delay shifts fromtd=-5 fs totd=5 fs, and the shifts of maximum emission energy correspond to the time delays of two pulses.

In Fig. 4(a), the subcycle probing pulse is at the rising edge of the laser field withtd=-5 fs, the maximum energy of HHG emission decreases obviously at this side. However,the maximum energy of HHG emission increases obviously at the same edge withtd=5 fs. This is the presentation of HHG time-frequency profiles that exhibits the subtle details of spectral and temporal structures for the whole energy range.In addition,in the high energy region,the time-frequency profiles show a netlike structure because only the intra-band harmonics are considered. Noticeably,it does not show short-and longtrajectories within each optical cycle. The features discussed here are not similar to those observed in the atomic case.

Fig. 4. Wavelet time-frequency spectra of the HHG in crystals: (a)td=-5 fs,(b)td=0 fs,(c)td=5 fs,respectively. The laser parameters used are the same as those in Fig.3.

Fig.5. The time profiles and dynamic phases of the 9th harmonic(H9)obtained from cross sections of the time-frequency spectrum in Fig.4:(a) td =-5 fs, (b) td =0 fs, (c) td =5 fs. The red dots indicate the corresponding dynamic phases.

To discuss more detailed spectral and temporal structures in the high-harmonic orders for the different time delays, a representative time profile for the 9th harmonic(H9)obtained from cross sections of the time-frequency spectrum in Fig. 4 is shown in Figs.5(a)-5(c). Note that the“dynamical phases”θ(tq) (denoted by red dots) obtained from the wavelet transform of the intra-conduction band current are also presented.The dynamical phasesθ(tq)at the instanttqcan be calculated bydω(t)=|dω(tq)|e-iS(tq), whereS(tq)=ωtq+θ(tq). The dynamical phases of the different time delays show different current trends. As is shown,the time profiles attd=0 fs show a relatively smooth and continuous variation as a function of time, mimicking that of the driving laser pulse, this result is similar to the atomic case. Particularly,the dynamical phase is almost a constant.For the case of the time delaytd=-5 fs andtd=5 fs,the time profiles show the fast-burst structure,and the dynamical phases also show some distinct changes. The HHG emission decreases obviously at the side of the subcycle laser pulse. It is in good agreement with the results shown in Fig.4.

3.1.2. Evolution of oscillation structures in momentum space

As discussed above,we have presented the HHG oscillation structures in the crystal driven by an MIR and subcycle laser pulse with a time delay, and have discussed the spectral and temporal features of oscillation structures using timefrequency analysis of wavelet transform. We know that the electron is a free particle in the crystal.Namely,the interaction between the electron and lattice potential is implicitly considered by using crystal momentum instead of true momentum.This is mathematically reasonable since the crystal momentum operator, as the translation operator with translation distance, has the infinite lattice constant, which commutes with the field-free Hamiltonian, and thus shares the eigenstates.Next, we extend an acceleration theorem for the description of the evolution of oscillation structures in momentum space.This method involves a definition of the time-dependent crystal momentumk(t):

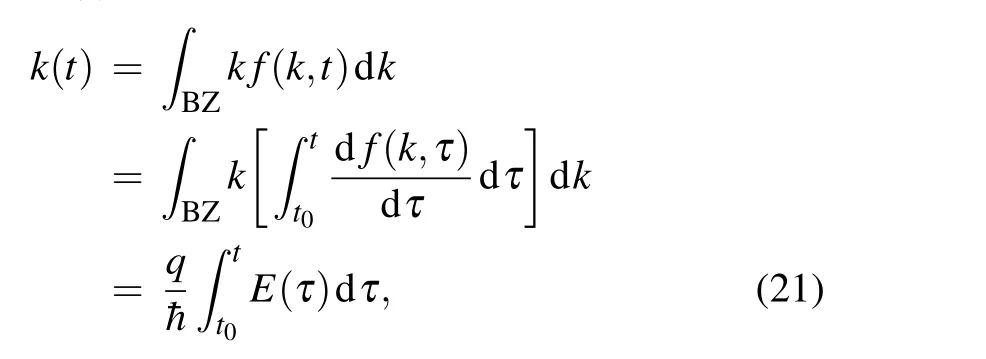
wheref(k,t) is the probability density distribution andE(τ)is the electric field at timet. As a result, using crystal momentum is somewhat like handling the problem in the frame rotating with the field-free Hamiltonian,and thereby the effect of lattice force, which is a term inside the field-free Hamiltonian, is implicitly considered and vanished. Therefore, the contribution of the radiation can be defined as an evaluation of group accelerationag(kc,t),

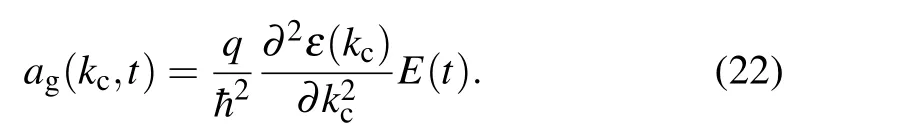
Notice that, unlike the group velocity, this group acceleration depends on both crystal momentum and time. We assume that the probability density in crystal momentum space is a narrow Gaussian distribution. Figure 6 shows the particle moves in the band along its trajectory,which is represented by the red curve. The effective mass is represented by the size of the ball and depends on the changes of the energy band.The color density indicates the radiation intensity determined by the effective mass and the intensity of the laser field. The charged particle with effective mass is pushed by the laser field force and starts to move in the band. It is easier to accelerate under the action of a laser pulse if the effective mass of a charged particle is relatively small, leading to higher radiation intensity. Furthermore, when the laser pushing force is so strong, the carrier can also produce strong radiation for a certain effective mass, since the larger laser force means that the charged particle is pushed or accelerated more strongly.This implies that the charged particle can produce strong radiation, because of a small effective mass of the carriers or the strong laser force enough to avoid considering its effective mass,when it happens to be at the position of the band structure. However, at those band positions marked by the blue ball, the carriers are essentially not radiated due to the larger effective mass of the carriers.

Fig.6. Schematic diagram depicting the relation of effective mass and the position of the particles in intra-band HHG of crystals. The result shows how the effective mass changes at different positions of the band.The particle is depicted as a ball,and it can be defined by calculating the absolute value of effective mass. The band used here is a simple cosine model band. The red curve is the trajectory of the particle in the crystal momentum space. The background represents various light emissions.

In Figs.7(a),7(b),and 7(c),the detailed radiation distribution in crystal momentum space is presented as a function of the time delaytd=-5 fs,td=0 fs, andtd=5 fs, respectively. It is very clearly seen that there is no emission in blue color regions and have the strong emission in red and green colors indicated. The red and green regions are called positive and negative emission regions. It is important in the sense of emission with polarization in direction of the positive and negative direction. Different time delays have different emission conditions, and the emission intensity varies obviously with time delaytd. By comparing the radiation intensity at the center of the Brillouin zone,we find that the effects of the few-cycle laser change the radiation interval and the radiation intensity in the time domain. This result is in good agreement with the spectral and temporal features of oscillation structures discussed above.

Fig.7. Distribution of the emission intensity of the HHG in the crystal:(a)td=-5 fs,(b)td=0 fs,(c)td=5 fs,respectively. The laser parameters used are the same as those in Fig.3. The red box indicates that the radiation intensity varies with the time delay.

3.2. Laser-induced HHG oscillation structure in multiband model

Based on the above discussion, the same scheme can be extended for probing subcycle spectral structures and dynamics from the practically mixed intra-and inter-band crystalline HHG spectrum. A linearly polarized laser field is considered to propagate through the crystal along the optical axis in the simulation. The laser-crystal interaction is simplified in one dimension along the laser polarization. The harmonic spectra can be obtained by the Fourier transform of the microscopic current. In Fig.8,we give the HHG spectra of the current calculated by solving the TDSE in velocity gauge. We have used 3 and 51 Bloch states in our expansion of wave function,which means that 3 and 51 bands are included in the calculations for eachkvalue, respectively. The second band has the deepest bound energy, so we choose it as the initially populated valence band. Based on the HHG obtained by the numerically Bloch basis,we have used the subcycle laser field as the previous one in the first subsection and given oscillation structures in the multi-band model in Fig.9.

When we use 3 band Bloch states in our expansion of wave function, the primary plateau is due to transitions between the valence band and the lowest conduction band. The oscillation structures of HHG are more complex, but variation trends are basically consistent with the results of our single-band model on the whole. In particular,we can observe significant enhancement and suppression of the HHG either in single-band or multi-band crystal systems at three specific time delays. Then we have compared the results of 51 Bloch states in expansion of wave function in Fig. 10, whereas the secondary plateau and more generally higher frequencies in the spectrum are due to contributions from higher-lying bands.The same conclusion has been confirmed under these different conditions.

Fig. 8. High-harmonic spectra calculated by solving the TDSE based on Bloch state basis in velocity gauge.

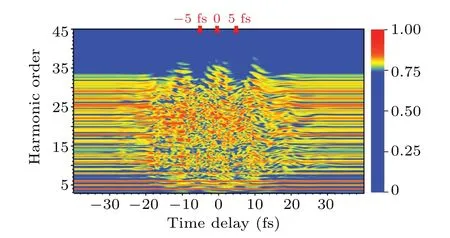
Fig.9. HHG spectra as a function of the time delay between MIR and subcycle laser pulse in 3 bands model.

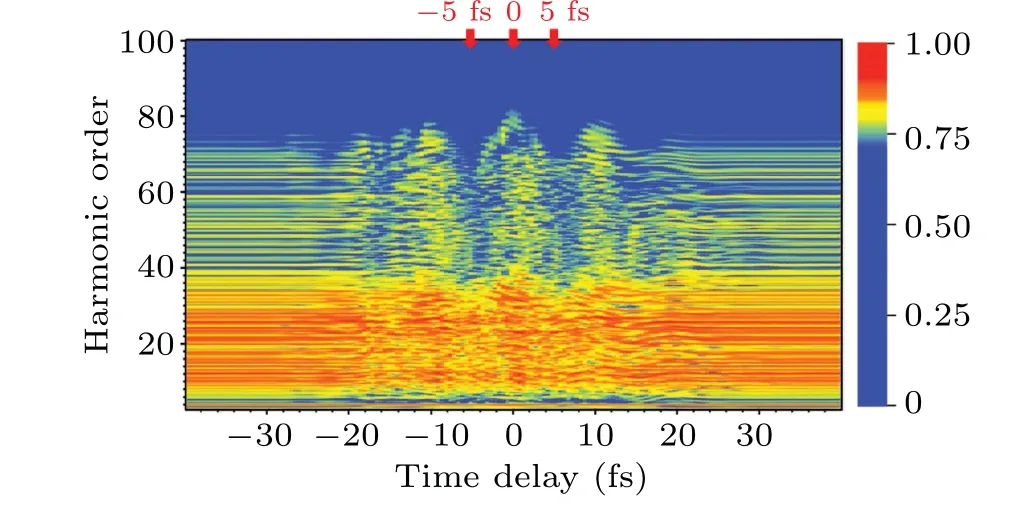
Fig.10. HHG spectra as a function of the time delay between MIR and subcycle laser pulse in 51 bands model.

4. Conclusion

In summary, we have systematically studied oscillation structures of HHG and the carrier dynamics of the HHG in mid-infrared laser fields subject to excitation by a subcycle laser pulse with a time delay. However, it is complex to directly analyze the HHG spectrum from the mixed intraand inter-band crystals because of multi-band contributions in crystals. Thus,it is significant to firstly explore the intra-band carrier contributions for us to understand the individual spectra features in crystals. We focus on two aspects. One is the emission characteristics of the time-frequency spectrum of the intra-band HHG,the other is the dynamical origin of the intraband HHG in the crystal momentum. To well understand the dynamical mechanism of the spectrum oscillation structures of subcycle intra-conduction band,we adopt an acceleration theorem for the description of the evolution of oscillation structures in momentum space, and the emission dynamics of the intra-band HHG generated by the MIR and a subcycle laser pulse with a time delay are clarified. Furthermore, to a comprehensive understanding of subcycle spectral structures and dynamics of HHG processes in crystals,the same scheme has been extended for probing the oscillation structures of multiband from the practically mixed intra- and inter-band crystalline HHG spectrum based on the Bloch state basis. The results indicate that the time-delay enhancement and suppression of the HHG related to subcycle pulse are observed at the given time delay in either single-band or multi-band crystal systems. Our result provides fresh insight to understand the crystal HHG processes excited by the sub-femtosecond pulse.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 12074239 and 91850209), the Natural Science Foundation of Guangdong Province, China(Grant Nos. 2020A1515010927 and 2020ST084), Department of Education of Guangdong Province, China (Grant Nos. 2019KTSCX038 and 2020KCXTD012), Shantou University (Grant No. NTF18030), the Natural Science basic Research Program of Shaanxi Province, China (Grant No. 2022JM-015), and Scientific Research Foundation of SUST(Grant No.2017BJ-30).