基于动态隔离的网络病毒传播建模

韩瑞锋，冯丽萍，王鸿斌，祝清意

(1.忻州师范学院 计算机系，山西 忻州 034000；2.重庆邮电大学 网络空间安全与信息法学院，重庆 400065)

大数据、云计算以及人工智能技术的快速发展把互联网应用推向了一个新的高潮，但与此同时，网络安全问题也越发突出，而网络病毒是造成网络安全问题的主要因素之一。2017年勒索病毒在全球爆发，影响到能源、金融、医疗、教育等众多行业。日常运营中，即使没有大规模病毒爆发事件，也会因各种利益驱使，不断出现木马、DDoS(Distributed Deny of Service)、僵尸网络等不同类型的网络病毒试图通过各种不正当手段破坏互联网的正常运行。据国家互联网应急中心报道，在2020年1月13日-19日，仅一周的时间，我国感染网络病毒的主机数量就达到44.7万[1]。在网络安全趋势日益复杂且严峻的形势下，被动的防御手段已远远不能满足有效抵抗网络病毒入侵的需求，因此网络病毒的自动防御技术已成为目前网络安全领域的一个研究热点。

为了加强网络安全防护，避免网络病毒的传播给国家、社会和个人造成巨大损失，国内外许多专家从不同角度研究了网络病毒防御策略，取得了良好效果[2-5]。由于网络病毒和流行病传播的相似性，在1991年，KEPHART将流行病动力学模型引入到网络安全领域[6]，后来，许多学者建立了考虑不同因素的流行病动力学模型来刻画网络病毒传播的特性，进而预测病毒传播的态势[7-10]。相关研究在网络病毒传播行为的刻画和预测方面发挥了很大作用。比如，ZOU et al[11]建立了双因素动力学模型，反映网络病毒爆发时的传播态势，仿真结果表明所建立的模型能准确反映“红色蠕虫”的传播特性。

在流行病动力学模型中，主要有两种基本类型，一种是简单的Susceptible-Infected(SI)模型[12]，这种模型不考虑任何人类行为对网络病毒传播的干扰因素，直接反映病毒的传播过程。另一种是经典的Susceptible-Infected-Recover(SIR)模型[13]，这类模型是在简单流行病模型基础上考虑了人类采取反病毒措施以后，网络病毒传播的动力学性态。后来许多学者以这两种模型为基础提出了考虑不同因素的网络病毒传播模型[14-16]。XIAO et al[14]提出了面向短消息服务的移动网络病毒传播SAIDR(susceptible-affected-infectious-suspended-recovered)模型，并且详细分析了基于该模型的蠕虫传播动力学特性。 王旭[15]在考虑网络结构的条件下，结合马尔科夫过程提出了连续SIS (susceptible-infectious-susceptible)模型，并且分析了该模型下网络病毒传播的阈值。HOSSEINI et al[16]考虑到移动设备对网络病毒传播的影响，提出了新的MD-SEIRS-V(mobile device-susceptible exposed infected recovered-viccine)模型，并且分析了网络病毒传播的稳定性条件。这些已有研究从不同角度建模人类行为对网络病毒传播控制的影响，为人们理解病毒传播行为以及如何采取相应措施控制病毒传播提供了良好的指导。考虑到隔离措施对抑制网络病毒传播的有效作用，FATIMA et al[17]提出了包含隔离状态的计算机病毒传播susceptible-latent-breakingout-quarantine-susceptible(LBQRS)模型，该模型假设已感染计算机病毒的节点以常量概率转化为隔离状态，随着时间的演化，处于隔离状态的节点以不同比例转化为其它状态。虽然作者在模型中引入了隔离状态，但是作者关注的重点是整个模型的动力学性态，并没有具体讨论隔离对控制计算机病毒的影响程度。YAO et al[18]认为理论研究中得出的隔离措施可以消除计算机病毒的传播结论在现实中并不能实现，原因是入侵检测系统发现病毒的过程是有延时的，基于此，作者在隔离状态中引入了延迟参数，重点讨论了延迟时长对计算机病毒传播的分叉动力学性质。以上文献表明，隔离措施确实可以有效抑制网络病毒的传播，但是，作者在研究时都假设节点是以固定比例被隔离的，事实上，在网络系统中由于入侵检测系统的识别误差和病毒本身的活动特性，隔离措施应该是服从一定规律的动态过程。因此，本文提出一种考虑动态隔离策略的动力学模型，并对模型进行分析和仿真，研究动态隔离策略对控制网络病毒传播的效果。

1 模型建立

本文建模的基本思想是：不管是利用系统漏洞还是不安全的用户行为，网络病毒的传播都会表现出异常，比如垃圾邮件的发送，攻击者会发送大量邮件到不同用户邮箱；而利用TCP漏洞，攻击者则会发出大量连接请求，导致资源崩溃。基于系统的异常发现，引入一种自动防御措施，即一旦检测系统发现异常行为，立即启动隔离系统。将该动态隔离措施引入到简单流行病模型来刻画网络病毒传播过程。 本文采用简单流行病模型的原因是为了刻画在没有其他反病毒措施的情形下，动态隔离措施对抑制网络病毒的效果。

简单流行病模型假设网络中的节点有两种状态：易感染状态Susceptible(S)和已感染状态Infected(I)，一旦某一节点被网络病毒感染，其状态就成为已感染I.也就是说，网络中的节点只存在一种从S→I的状态转移。用S(t)表示t时刻易感染的节点数；I(t)表示已感染的节点数；N(t)表示节点总数，那么有：N(t)=S(t)+I(t).

本文考虑网络结构是同构的情况，也就是易感染节点和已感染节点接触的机会是均等的，当已感染节点I接触易感染节点S时，S就可能被感染，成为I，假设单位时间内一个已感染节点和网络中易感染节点接触的几率为k，接触感染率为α.那么，单位时间内易感染节点被感染的数量为：kαS(t)I(t).令β=kα，那么，从t到t+1时间段，S(t)和I(t)的变化关系可表示为：

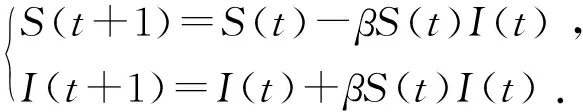
(1)

式(1)即为简单流行病模型，该模型反映的是没有任何人为措施的情况下，网络病毒的传播规律。事实上在维护网络安全方面，人类会采取一切可能的办法抑制病毒的大规模扩散。受现实中流行病爆发时采取隔离措施的启发，本文主要考虑动态隔离措施对网络病毒传播性能的影响，在简单流行病模型(1)的基础上加入反映动态隔离措施的参数，构建本文模型。在网络运行过程中，如果异常检测系统发现有可疑行为(端口扫描异常、SYN连接请求异常、IP地址访问异常等)，那么就立刻告警并选择对该可疑行为进行隔离阻断，也就是采取“证明无罪之前先假定有罪”策略。考虑系统存在检测错误的情况，所以初次隔离时间不会太长，比如几秒，然后自动解除隔离，这样，即使错误地隔离了正常请求，根据经验，短暂的隔离不会对正常用户造成影响。如果发现下一次行为仍然可疑，那么再进行隔离，而且隔离时间也会比第一次增长，也就是，对某一可疑行为而言，隔离时间是动态增长的，第i+1次的隔离时间要大于第i次的隔离时间。当某一节点可疑行为的次数达到设定的阈值Ω时，就封锁该节点的网络访问权限。另外，如果入侵检测发现某一节点的可疑行为后，经安全人员检查确定为恶意入侵，那么，就直接将该节点拉入黑名单，封锁其网络访问权限，不会给予其下一次访问网络的机会。

定义1隔离动态增长因子δ为网络中某一可疑行为第i+1(i=1,2,3,…,n,n≤Ω)次隔离时间相比于第i次隔离时间的增量。

δ和Ω的值由节点可疑行为的类别、安全危险级别以及网络管理员的经验等因素确定。

采取动态隔离措施的优点是当异常检测系统发出告警以后，安全人员检查网络是否确实存在安全入侵的行为所需要的时间远远大于网络病毒传播的时间，及时隔离可疑行为可以有效避免预防措施不及时造成的损失。另一方面，由于每一次对可疑行为的隔离时间很短，所以即使存在错误地把正常请求误判为入侵行为的情况，正常用户的服务也不会受到影响，相反，由于病毒爆发时存在时间短、速度快的特点，即使短暂的隔离也对病毒大规模扩散产生影响。

本文的动态隔离模型遵循如下假设：

假设1 可疑节点被隔离的时间为T；

假设2 易感染节点的行为遵循参数为λ1的泊松分布；

假设3 已感染节点的行为遵循参数为λ2的泊松分布(因为已感染节点可能会在某段时间内频繁发出请求，所以这里认为λ2≥λ1).

根据现实情况，异常检测程序可能会把正常请求判断为异常，假设判断错误的概率为λs(0≤λs<1).令Qs(t)表示t时刻被隔离的易感染节点数，根据假设(2)，在(t-T)～t时间段内，请求n次服务的易感染节点的概率为：

(2)

那么，t时刻被隔离的易感染节点数为：

(3)

同理，用QI(t)(0≤λI≤1)表示t时刻被隔离的已感染节点数，可以求出：

(4)

其中，λI表示已感染节点行为被判断为可疑的概率。

结合式(1)和以上描述，具有动态隔离措施的网络病毒传播模型可表示为图1.

图1用公式可表示为：

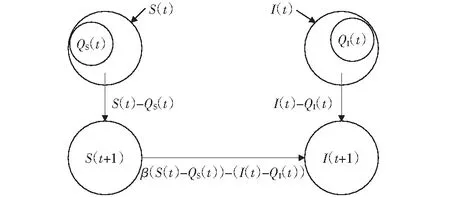
图1 具有动态隔离措施的网络病毒传播模型Fig.1 Network virus propagation model with dynamic quarantine measure

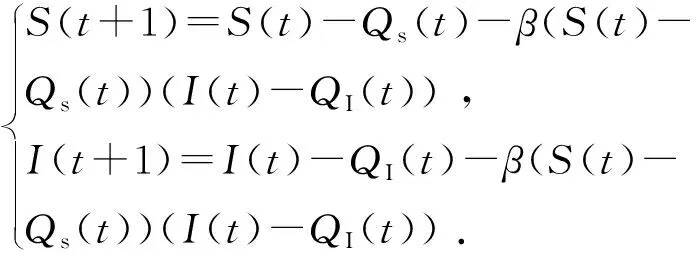
(5)

将式(3)和(4)代入式(5)有：

(6)

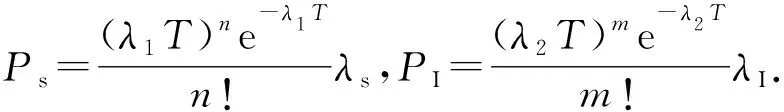
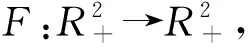
2 实验仿真

本章实验环境采用Matlab2016R，实验方法采用离散时间迭代法，实验目的主要是：1) 比较采取隔离措施和不采取隔离措施两种情况下，网络病毒的传播过程；2) 节点隔离时间长短对网络病毒传播的影响；3) 比较本文模型和文献[17-18]简化后的模型所反映的网络病毒传播过程。

实验过程中模型参数取值，设网络规模大小为1 000个节点，不失一般性，假设初始状态时已感染节点数很少，取I(0)=10，那么S(0)=990，感染率β的值参考文献[19]的计算方法，数量级为10-4，本文取β=0.000 1，其他参数根据其实际物理意义取值如表1所示。

1) 首先，比较采取隔离措施和不采取隔离措施两种情况下网络病毒的传播情况，也就是对比本文模型(系统(6))和简单流行病模型(系统(1))反映的网络病毒传播行为随着时间演化的传播趋势。分别对本文提出的系统(6)和传统的系统(1)进行2 000次迭代模拟，结果如图2所示。

图2中的曲线分别为采取隔离措施以后(本文提出的模型)和未采取隔离措施(简单流行病模型)时网络中易感染节点数和已感染节点数随时间的变化规律。仿真结果表明，采取隔离措施以后，网络病毒的传播速度明显减慢。如果不采取隔离措施，大约20 min的时间，网络中节点就全部被感染，而采取隔离措施以后，节点全部被感染的时间延长至大约50 min，说明隔离措施可以有效延缓病毒大规模扩散的速度，为管理员施行控制措施争取更多的时间。另一方面，可以观察到，无论是否采取隔离措施，网络中的节点最终几乎会全部被感染。

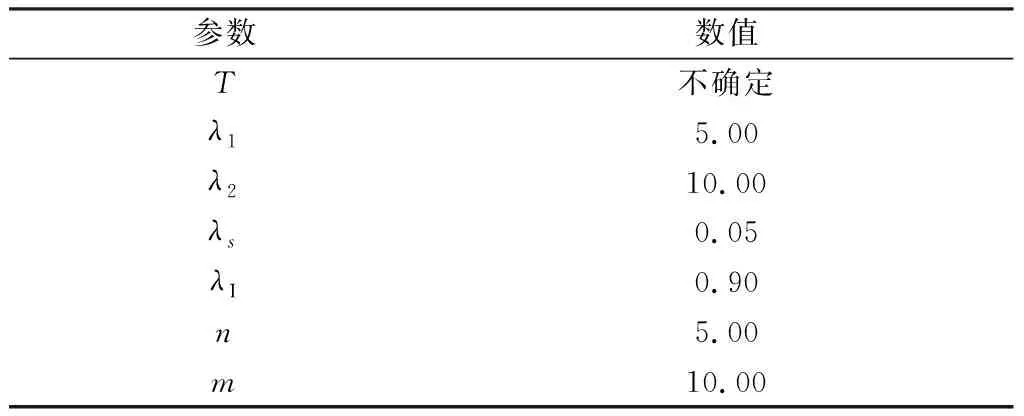
表1 实验参数及其取值Table 1 Value of parameters

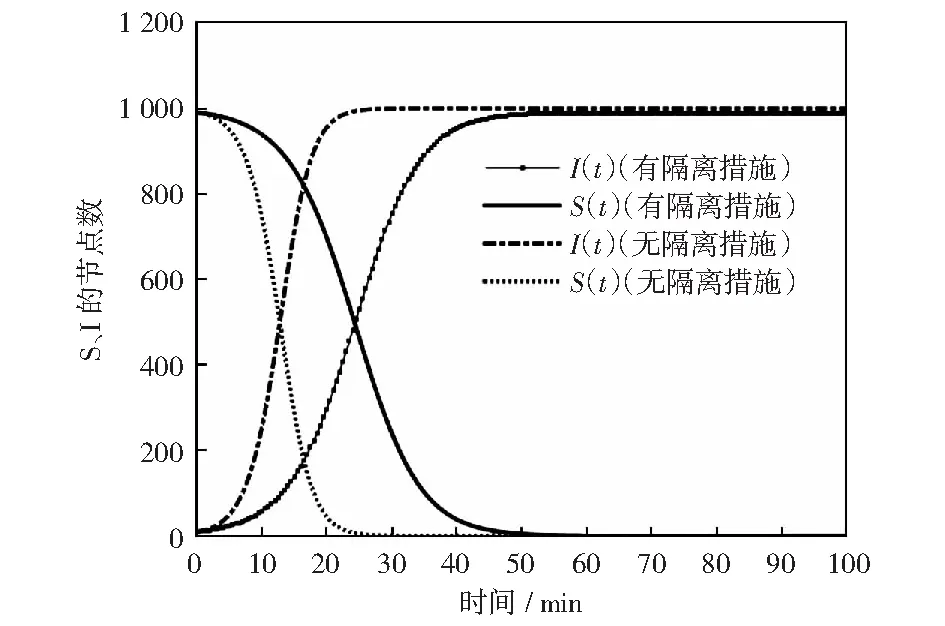
图2 网络病毒传播比较Fig.2 Network virus propagation comparison

采取隔离措施以后网络病毒传播速度会减慢的原因是：可疑节点被隔离以后，每个离散时间段网络中易感染和已感染节点都会比没有隔离措施时减少，在地址空间一定的背景下，这相当于稀释了感染密度，所以网络病毒探测到易感染节点的时间就会增长。而最终网络节点几乎全部被感染是因为：节点的被隔离时间很短(本实验为0.2 min)，在隔离节点被释放以后又成为被感染节点或者感染其他节点，所以最终网络中几乎全部节点都被感染。此实验结果表明，采取短暂的隔离措施只会延缓病毒传播速度，并不会减小其感染规模，所以，为了达到控制病毒大规模传播的目的，需要根据实际网络运行环境采取动态隔离措施。

2) 模拟隔离时间长短对网络病毒传播的影响(即采取动态隔离措施)。隔离时间t分别取0.2、0.3、0.4和0.5 min，即隔离动态增长因子δ为0.1，异常行为阈值Ω最大为0.5，其他参数值不变，对系统(6)进行2 000次迭代运算，模拟结果如图3所示。

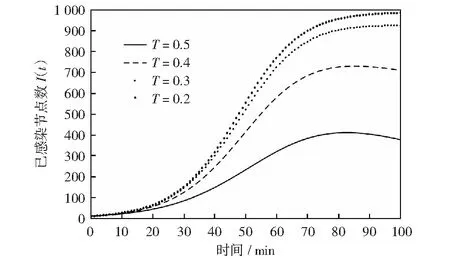
图3 不同隔离时间对应的已感染节点数随时间变化图Fig.3 Trajectories of I(t) with different T

从图3可以观察到，在网络病毒传播的开始几分钟内，微小的隔离时间差对网络病毒传播速度和规模影响并不太明显。随着时间的推移，大约到了20 min以后，隔离时间为0.5 min时明显比隔离时间为0.2、0.3和0.4 min时网络病毒感染的速度要慢，而且最终感染规模也明显减小，大约为网络节点的28%.也就是说，可疑节点隔离的时间越长，网络病毒传播得越慢，感染规模也越小。这是因为隔离时间增长以后对隔离节点的释放速度会变慢，导致隔离节点会慢慢累积，从而网络中活动节点就会减少，相应地被感染节点的规模也会变小。

从图2和图3发现，当隔离时间小于等于0.2 min时，动态隔离措施会延缓网络病毒的传播时间，但是对传播规模不会有太大影响；当隔离时间达到0.3 min时，无论从规模上还是时间上都会对网络病毒的传播产生一定影响；当隔离时间超过0.4 min时，病毒感染的速度明显减慢，感染规模也明显减小。此实验表明，动态隔离措施可以有效抑制网络病毒的传播，根据实际网络运行环境选取合适的隔离时间，既可以为网络管理员进一步确定当前可疑行为是否是入侵行为争取时间，同时也可以有效降低网络节点被感染规模。

3) 接下来观察隔离时间取不同值时，网络中被隔离节点数随时间的变化情况。实验参数取值同2)，仿真结果如图4所示。

图4是不同隔离时间长度对应的被隔离的易感染节点数数随时间变化关系。从图4可以观察到，被隔离的易感染节点数是随时间递减的，这个趋势和图2反映的相同，这是因为随着时间的演进，网络中易染节点逐渐被网络病毒感染变成了已感染节点。

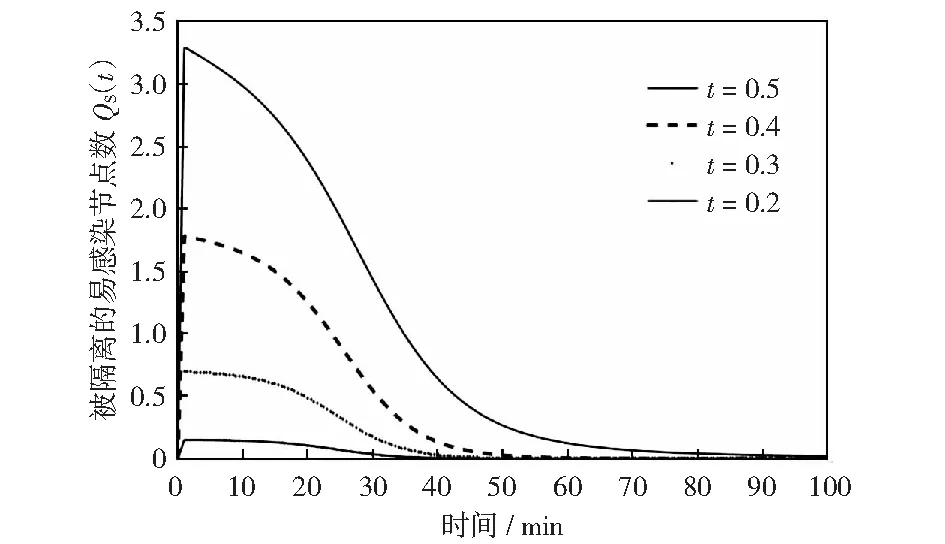
图4 当隔离时间不同时被隔离节点数随时间变化Fig.4 Trajectories of Qs with different quarantine time

为了更明晰地呈现网络中被感染的节点数和已隔离节点数随时间变化的关系，呈现了图5的演化曲面图(隔离时间为0.2 min).可以观察到，图5中各要素的变化趋势与图3和图4中反映的变化是一致的。

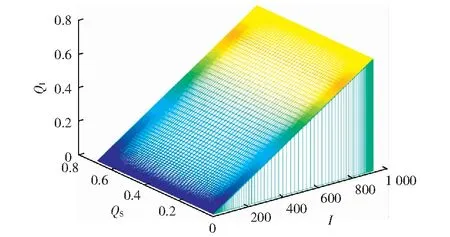
图5 采取隔离措施时网络病毒传播曲面图Fig.5 Curve of network virus propagation with quarantine

4) 最后，将本文模型和简化后的已有模型[17-18]进行比较。简化已有模型的原因是为了消除模型中考虑的其他影响因素，只考虑隔离措施对病毒传播过程的影响，提高与本文模型的可比性。文献[17]和[18]简化后可表示为：

(7)

为了和本文模型进行比较，式(7)中S和I的初始值与图2相同，Q的初始值取0，感染率β的取值也与图2相同，参数α和γ取值0.000 1，比较结果如图6.

从图6可以看到，本文的动态隔离模型和已有模型(将隔离状态引入病毒传播模型)的仿真结果拟合很好，说明本文模型可以有效反映具有隔离措施的病毒传播过程。据此，在实际网络防护管理过程中，根据IDS的检测结果，可以根据实际情况动态调整可疑节点的隔离时间，以达到最佳病毒防御效果。

图6 本文模型和已有模型的比较Fig.6 Comparation of this model and existing models

3 结束语

由于网络病毒传播与现实中流行病传播具有相似性，受流行病爆发时采取隔离措施的启发，本文基于简单流行病动力学SI模型，提出了考虑隔离策略的网络病毒防御模型，从另外一个视角探讨了反病毒措施(动态隔离)对抑制网络病毒传播的影响，与以往模型不同，本文考虑到病毒传播行为的离散特性，建立的是离散动力学模型。在考虑网络节点行为符合泊松分布的情况下，导出了易感染节点和已感染节点的隔离率，进而给出了任意时刻被隔离节点数的数学表达式。进一步，通过Matlab平台模拟了本文模型和传统简单SI模型反映的网络病毒传播随时间的演化过程，结果表明，本文模型中提出的动态隔离措施可以有效减慢解网络病毒爆发的速度，可以为网络管理员争取宝贵的网络病毒控制时间。另外，通过实验观察了隔离时间长短(动态隔离措施)对网络病毒传播速度和规模的影响程度，考虑到不能影响正常网络服务请求，仿真实验设置较小的隔离时间进行观察，这与现实需求是一致的。实验结果表明，隔离措施可以有效减慢网络病毒的传播速度，为采取有效的病毒防御策略争取充分时间。研究结果可以为异常检测系统在响应网络入侵事件时提供理论指导，也可以为网络管理员维护网络提供借鉴。今后结合实际网络运营状况探究具有现实意义的隔离时间、隔离动态增长因子以及异常行为阈值，是需要进一步研究的内容。